NCERT Solutions for Exercise 11.2 Class 9 Maths Chapter 11

NCERT Solutions for Exercise 11.2 Class 9 Maths Chapter 11 - Constructions

Edited By Sumit Saini | Updated on Dec 29, 2021 06:17 PM IST

NCERT Solutions for Class 9 Maths chapter 11 exercise 11.2 introduces us with the construction of triangles till now we have learned about how to construct the bisector of a given angle, and the perpendicular bisector of a given line segment must be constructed. and to create a 60-degree angle at the starting point of a given ray.NCERT solutions for Class 9 Maths chapter 11 exercise 11.2 is based on the construction of triangles using the prior knowledge of exercise 11.1 Class 9 Maths and the congruence of triangles as covered in chapter seventh Class 9. All the construction in the NCERT solutions for Class 9 Maths chapter 11 exercise 11.2 is carried out with the help of compass and ruler but we can use a protector to re-check if construction is accurate. Actually, it is very helpful as it cross-examines the whole construction. Along with Class 9 Maths chapter 11 exercise 11.2, the following exercises are also present.

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

Constructions Class 9 Maths Chapter 11 Excercise: 11.2
Q1 Construct a triangle ABC in which , and .
More About NCERT Solutions for Class 9 Maths Exercise 11.2
Benefits of NCERT Solutions for Class 9 Maths Exercise 11.2
NCERT Solutions of Class 10 Subject Wise
NCERT Solutions for Class 9 Maths

Constructions Exercise 11.1

Constructions Class 9 Maths Chapter 11 Excercise: 11.2

Q1 Construct a triangle ABC in which $BC = 7cm$ , $\angle B = 75\degree$ and $AB + AC = 13 cm$ .

Answer:

The steps of construction are as follows:

Step 1: Draw a line segment BC of 7cm length. Taking the help of protractor make an $\angle XBC = 75^{\circ}$ .

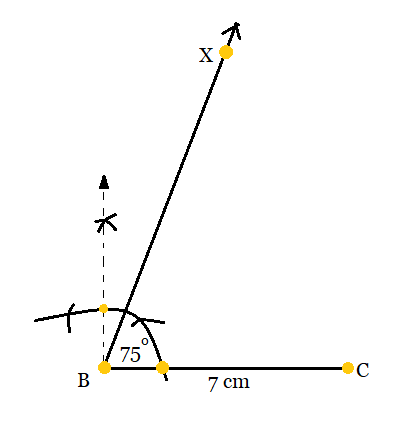
1640601458338

Step 2: Now, cut a line segment BD having 13 cm on BX which is $(AB+AC).$

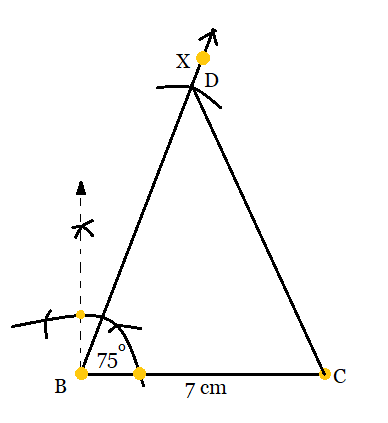
1640601468104

Step 3: Now, join CD.

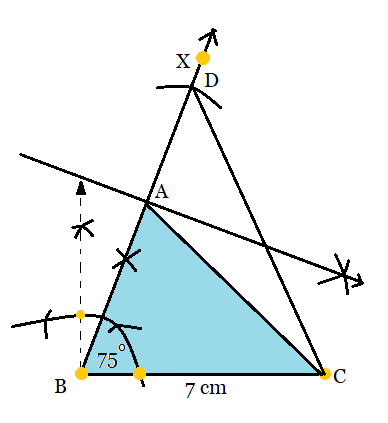
1640601479666

Step 4: Draw a perpendicular bisector of CD to intersect BD at a point A. Join AC. Then ABC is the required triangle

Hence, the required triangle is ABC.

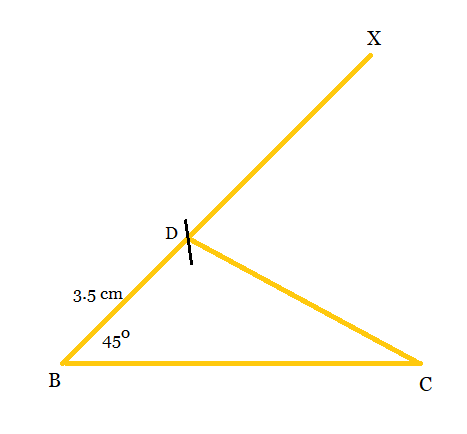
Q2 Construct a triangle ABC in which $BC = 8cm$ , $\angle B = 45\degree$ ° and $AB - AC = 3.5cm$

Answer:

The steps of construction to be followed:

Step 1: Draw a line segment BC = 8cm and make an angle of $45^{\circ}$ at point B i.e., $\angle XBC.$

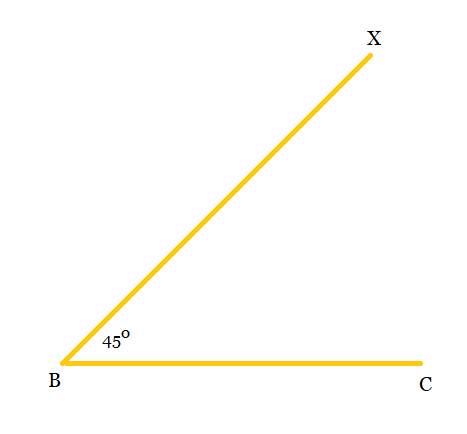
1640601500495

Step 2: Now, cut the line segment BD = 3.5 cm on ray BX. i.e. $(AB-AC)$ .

Step 3: Join CD and draw a perpendicular bisector of CD i.e., PQ.

1640601513380

Step 4: Let the perpendicular bisector of CD intersects BX at point A. Then,

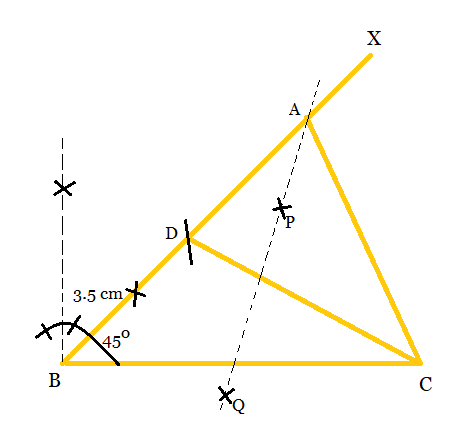
1640601551723

Step 5: Join AC, to get the required triangle $\triangle ABC.$

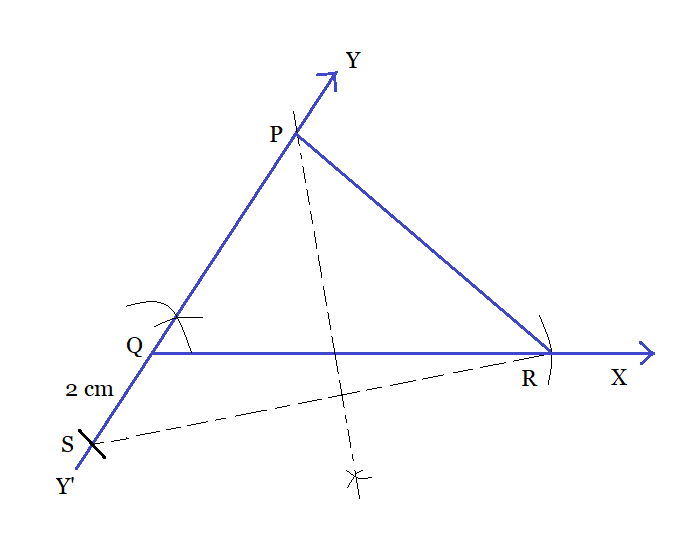
Q3 Construct a triangle PQR in which $QR = 6cm$ , $\angle Q = 60 \degree$ and $PR -PQ = 2cm$ .

Answer:

The steps of construction to be followed:

Step 1: Draw a ray QX and cut off a line segment QR which is equal to 6 cm in length.

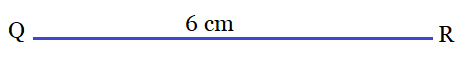
1640601586225

Step 2: With an angle of $60^{\circ}$ with QR, construct a ray QY and extend it to form a line YQY'.

Step 3: Now, cut off a line segment QS equal to 2 cm from QY' and join RS.

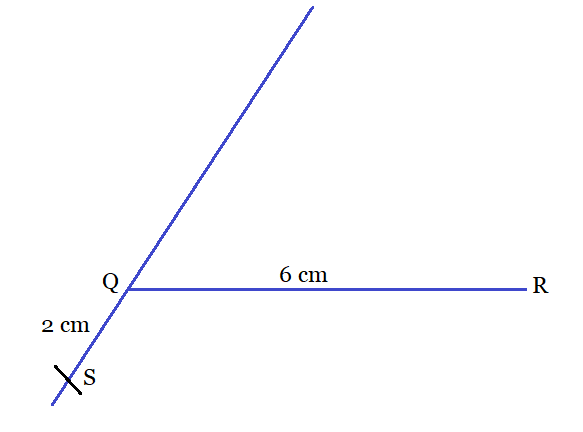
1640601600248

Step 4: Draw a perpendicular bisector of RS which intersects QY at a point P.

Step 5: Join PR to get the required triangle $\triangle PQR.$

1640601611912

Q4 Construct a triangle XYZ in which $\angle Y = 30\degree$ , $\angle Z = 90\degree$ ° and $XY + YZ + ZX = 11 cm$ .

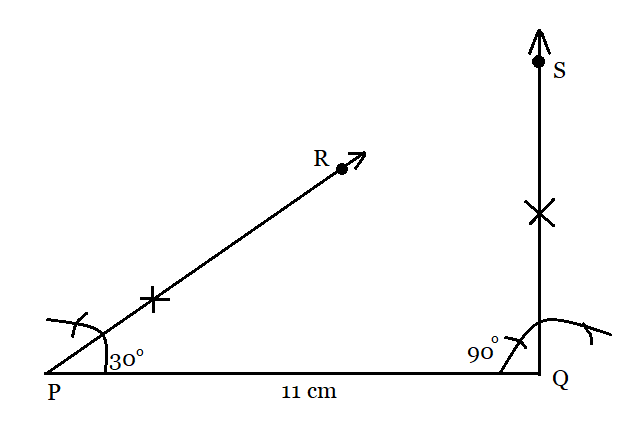
Answer:

The steps of construction to be followed:

Step 1: For given $XY+YZ+ZX = 11 cm$ , a line segment $PQ =11 cm$ is drawn.

Step 2: At points, P and Q angles of $\angle RPQ = 30^{\circ}$ and $\angle SQP =90^{\circ}$ are constructed respectively.

1640601637611

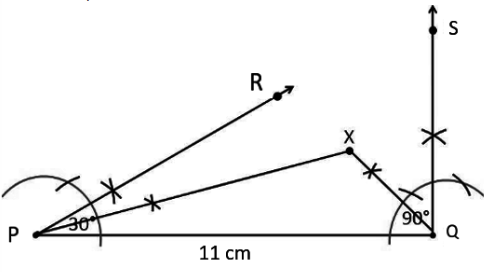
Step 3: Now, bisects the angle RPQ and SQP. The bisectors of these angles intersect each other at a point X.

1640601651930

Step 4: Construct the perpendicular bisector of PX and QX, name them as TU and WV respectively.

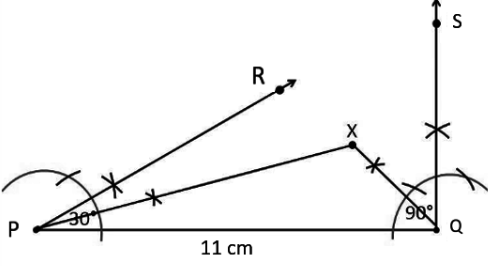
1640601673964

Step 5: Let the bisector TU intersect PQ at Y and bisector WV intersect PQ at Z. Then XY and ZY are joined.

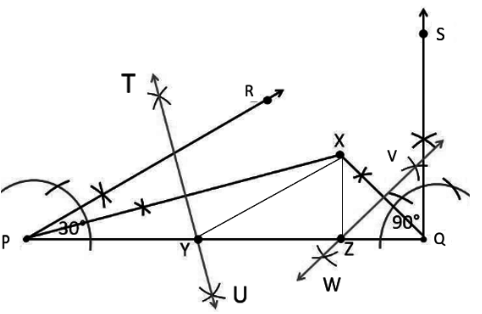
1640601685870

Therefore, $\triangle XYZ$ is the required triangle.

Q5 Construct a right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.

Answer:

The steps of construction to follow:

Step 1: Draw a ray BX and Cut off a line segment $BC=12cm$ from the ray.

1640601714690

Step 2: Now, construct an angle $\angle XBY = 90^{\circ}$ .

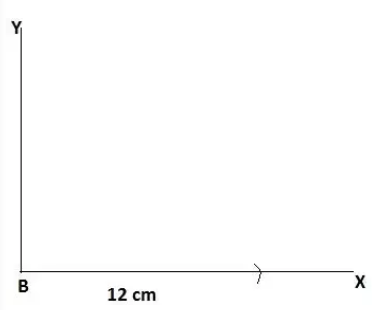
1640601724612

Step 3: Cut off a line segment BD of length 18 cm on BY. Then join the CD.

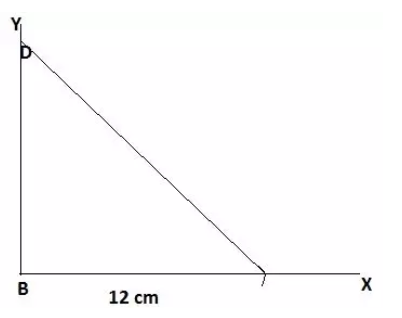
1640601736897

Step 4: Now, construct a perpendicular bisector of CD which intersects BD at A and AC is joined.

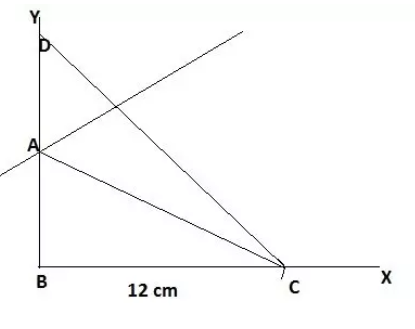
1640601751004

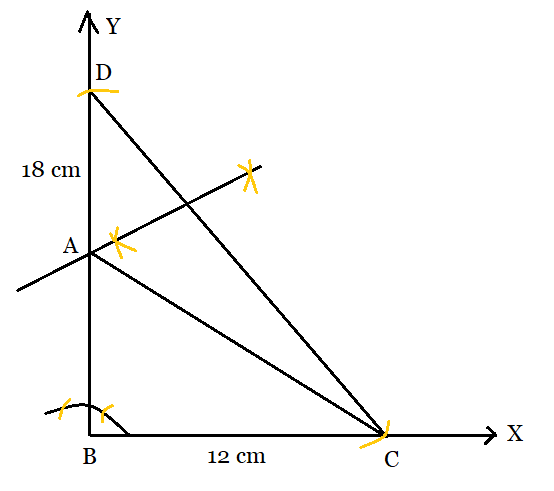
1640601761290

Thus, the constructed triangle is ABC.

Benefits of NCERT Solutions for Class 9 Maths Exercise 11.2

Class 9 Maths chapter 11 exercise 11.2 covers the topic of construction of triangle in three different way as provided in Class 9 Maths chapter 11 exercise 11.2
NCERT Class 9 Maths chapter 11 exercise 11.2 , will be helpful in Class 11 Maths chapter 11 construction.
Construction is a very important topic of an entrance exam JEE Main (joint entrance exam - 2) known as B-arch
Construction is base engineering in physics and mechatronic

Also See:

NCERT Solutions of Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. What should be used in construction of problems in NCERT solutions for Class 9 Maths exercise 11.2 ?

We should only use ruler and compass to construct the figures

2. Can we use a protractor to construct figures ?

No we cannot use protractor to construct figures we can only use to recheck the figure

3. When is a triangle unique ?

(i) two sides and the included angle is given,

(ii) three sides are given,

(iii) two angles and the included side is given and,

(iv) in a right triangle, hypotenuse and one side is given.

4. How many new constructions are introduced before exercise 11.2 Class 9 Maths ?

three new constructions are introduced before Exercise 11.2 Class 9 Maths

5. Which rules of congruence are used in NCERT solutions for Class 9 Maths exercise 11.2 ?

SAS (side angle side)

Side by side, side by side SSS

ASA (angle side angle)

RHS (right hand side)

6. How many questions are answered in the NCERT answers for Class 9 Mathematics chapter 11 exercise 11.2?

Class 9 Mathematics chapter exercise 11.2 has 5 questions.

7. How many solved examples are there before the NCERT answers for Class 9 Mathematics chapter 11 exercise 11.2?

Before NCERT solution for Class 9 Mathematics chapter 11 exercise 11.2 there are 1 solved examples

8. What kinds of questions do the NCERT answers for Class 9 Mathematics chapter 11 exercise 11.2 cover?

All the questions covered in the Class 9 Maths chapter exercise 11.2 was about construction. It included the bases of the construction covered before exercise in theory part.

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 03, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 03, 2024

How to Prepare for Science Olympiads: The Ultimate Study Plan

Dec 03, 2024

Silverzone STEM Result 2024-25 – Check STEM Olympiad Results Online

Dec 02, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 02, 2024

Silverzone Commerce Olympiad Answer Key 2024: ICSI Question Paper Solution

Dec 02, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 02, 2024

Silverzone ABHO Result 2024-25 - Check Akhil Bhartiya Hindi Olympiad Results Here

Dec 02, 2024

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:05 November,2024 - 07 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Manipur Board 12th Examination

Application Date:11 November,2024 - 11 December,2024

Exam Pattern

Admit Card

Result

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 December,2024

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 December,2024

Admit Card

Result

Andhra Pradesh Board of Intermediate Education Examination

Others:12 November,2024 - 05 December,2024

Exam Pattern

Mock Test

Admit Card

View All School Exams

Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is