NCERT Solutions for Class 9 Science Chapter 7 Motion - Free PDF
Have you ever questioned yourself about how sportsmen can measure their speed or why a vehicle becomes slower when the brakes are pressed? Motions form a key component of our everyday existence, be it in a roller coaster ride, in a bus or on a street walk. Class 9 Science Chapter 7 - Motion is a topic that delves into the scientific concepts that support these common processes to enable the student to relate what he has been learning in the classroom with what he experiences in life.
This Story also Contains
- Class 9 Science Chapter 7 - Motion Question Answers: Download Solution PDF
- Class 9 Science Chapter 7 - Motion Question Answers: In-text Questions
- NCERT Solutions for Class 9 Science Chapter 7 Motion: Solved Exercise Questions
- Class 10 Science NCERT Chapter 7: Higher Order Thinking Skills (HOTS) Questions
- NCERT Solutions for Class 9 Science Chapter 7 Motion - Key Topics
- NCERT Solutions for Class 9 Science Chapter 7 Motion - Important Formulas
- Approach to Solve Questions of Class 9 NCERT Chapter 7: Motion
- Benefits of NCERT Solutions for Class 9 Science Chapter 7 Motion
- What You Will Learn from NCERT Solutions for Class 9 Science Chapter 7: Motion?
- NCERT Solutions for Class 9 Science Chapter-wise
- NCERT Solutions for Class 9 - Subject Wise
- NCERT Books and NCERT Syllabus

NCERT Solutions for Class 9 Science Chapter 7 - Motion are perfectly designed to be interesting and effective in learning, with the subject experts working smoothly on easy-to-understand language. All important notions, such as speed, velocity, acceleration, displacement, and distance, are included in these NCERT Solutions for Class 9 Science Chapter 7 - Motion, and a variety of solved problems and practice problems are provided to help the students develop a better understanding of the concepts and practice using numerical problems. Step-by-step NCERT solutions of in-text questions, exercise questions, and HOTS (Higher Order Thinking Skills) problems are also beneficial to students, and it is easier to learn such topics as types of motion, motion graphs, and equations of motion. These Motion NCERT Solutions are ideal for examination preparation, self-study, and revision, as the students will learn the theory and numbers effectively.
Class 9 Science Chapter 7 - Motion Question Answers: Download Solution PDF
Class 9 Science Chapter 7 - Motion question answers are provided to students in a well-structured and easy-to-follow format, giving clear answers to all in-text and exercise questions in the NCERT textbook. These solutions embrace significant concepts such as speed, velocity, acceleration, displacement, distance, motion graphs, and equations of motion, which make studying and exam preparation less difficult and effective. These NCERT solutions can help the student to reinforce his or her knowledge, practice numbers, and revise in a hurry before the examination.
Class 9 Science Chapter 7 - Motion Question Answers: In-text Questions
Class 9 Science Chapter 7 Motion In-text Questions also offer step-by-step answers to the questions in the NCERT textbook in a general, easy-to-understand format. Motion NCERT Solutions assist in the clarification of concepts like speed, velocity, acceleration, distance and displacement and also simplify numerical and conceptual problems. They can be used to prepare, revise and do homework with ease.
Topic 7.1 Describing Motions
Answer:
Yes, an object that has moved through a distance can have zero displacement.
If an object moves and returns to the original position, the displacement will be zero. Consider the movement in a circular path. A man walks from point A in a circular path in a park and comes back to point A.
The distance travelled is equal to the circumference of the circular path, but the displacement is zero.
Answer:
Side of the square field $=10 \mathrm{~m}$
$\therefore$ The perimeter of the square $=4 \times 10=40 \mathrm{~m}$
According to the question,
He completes 1 round in $40 s$.
$\therefore$ Speed of the farmer $=\frac{40}{40}=1 \mathrm{~m} / \mathrm{s}$
$\therefore$ Distance covered in $2 \min 20 s(=140 s)=140 \times 1=140 m$
Now,
Number of round-trip completed travelling $=\frac{140}{40}=3.5$
We know, in 3 round-trips, the displacement will be zero.
In 0.5 rounds, the farmer will reach a position diametrically opposite to his initial position.
$
\therefore \text { Displacement }=A C=\sqrt{\left(A B^2+B C^2\right)}=\sqrt{\left(100^2+100^2\right)}=10 \sqrt{2} m
$
Q 3. Which of the following is true for displacement?
(b) Its magnitude is greater than the distance travelled by the object.
Answer:
(a) The first statement is false. Because displacement can be zero when the initial point coincides with the final point.
(b) The second statement is false. The magnitude of displacement can never be greater than the distance travelled by the object. It can be either equal or less.
Topic 7.2 Measuring the Rate of Motion
Q 1. Distinguish between speed and velocity.
Answer:
| Speed | Velocity |
|
Speed is the distance travelled by an object in a unit of time |
Velocity is the speed of an object moving in a definite direction. |
| Speed is a scalar quantity | Velocity is a vector quantity |
| Speed does not depend on the direction | Velocity changes with a change in direction |
| Speed can never be negative | Velocity can be positive, negative or zero. |
Answer:
When the total distance travelled by the object is equal to the displacement, the magnitude of the average velocity will be equal to the average speed. Average speed is the total distance divided by the time taken, whereas average velocity is the total displacement uponthe time taken.
Q 3. What does the odometer of an automobile measure?
Answer:
An odometer is a device that measures the total distance travelled by an automobile.
Q 4. What does the path of an object look like when it is in uniform motion?
Answer:
An object has a uniform motion if it covers an equal distance in an equal interval of time (which implies speed is constant!). So the path can be straight or curved.
For eg, consider a circular path. For understanding purposes, divide the circumference of the circle into six equal parts, each subtending $60^{\circ}$ at the centre. The object covers each equal part in an equal amount of time. Hence, by definition, this object is in uniform motion.
Answer:
Given that the signal travels at the speed of light, $v=3 \times 10^8 m s^{-1}$.
Time taken by the signal $=5 \mathrm{~min} s=5 \times 60 \mathrm{~s}=300 \mathrm{~s}$
Let the distance of the spaceship from the ground station be $D m$
We know, Speed $=\frac{\text { Distancetravelled }}{\text { Timetaken }}$
$
\begin{aligned}
& \Rightarrow v=\frac{D}{t} \\
& \Rightarrow D=v \times t=3 \times 10^8 \times 300 \\
& \Rightarrow D=9 \times 10^{10} \mathrm{~m}
\end{aligned}
$
Topic 7.3 Rate of Change of Velocity
Q 1. When will you say a body is in
Answer:
(i) If the velocity of an object travelling in a straight line increases or decreases by equal amounts in equal intervals of time, then the acceleration of the object is said to be uniform. For example, an apple has a free-fall motion.
(ii) On the other hand, if the velocity of the object increases or decreases by unequal amounts in equal intervals of time, then the acceleration of the object is said to be non-uniform. For example, A car travelling along a straight road increases its speed by unequal amounts in equal intervals of time.
Q.2 A bus decreases its speed from 80 km h-1 to 60 km h-1 in 5 s. Find the acceleration of the bus.
Answer:
(We know, $1 \mathrm{~km}=1000 \mathrm{~m} ; 1 \mathrm{hr}=3600 \mathrm{~s}$ )
Given, Initial speed of the bus, $u=80 \mathrm{kmh}^{-1}=\frac{80 \times 1000}{3600}=\frac{200}{9} \mathrm{~ms}^{-1}$
The final speed of the bus, $v=60 \mathrm{kmh}^{-1}=\frac{60 \times 1000}{3600}=\frac{100}{6} \mathrm{~ms}^{-1}$
Time is taken, $t=5 s$
We know, $v=u+a t$
$
\begin{aligned}
& \Rightarrow \frac{100}{6}=\frac{200}{9}+a(5) \\
& \Rightarrow 5 a=\frac{900-1200}{6 \times 9}=\frac{-300}{6 \times 9} \\
& \Rightarrow a=-\frac{100}{9}=-1.11 m s^{-2}
\end{aligned}
$
The negative sign implies retardation.
Therefore, the acceleration of the bus is $-1.11 m s^{-2}$
Or, the retardation(de-acceleration) of the bus is $1.11 m s^{-2}$
Answer:
$($ We know, $1 \mathrm{~km}=1000 \mathrm{~m} ; 1 \mathrm{hr}=3600 \mathrm{~s})$
Given that the train starts from rest. Hence, the initial speed of the train $=0 k m h^{-1}=0 m s^{-1}$
Final speed of the train $=40 \mathrm{kmh}^{-1}=\frac{40 \times 1000}{3600}=\frac{100}{9} \mathrm{~ms}^{-1}$
Time taken, $t=10 \mathrm{~min}=10 \times 60 \mathrm{~s}=600 \mathrm{~s}$
We know, $v=u+a t$
$
\begin{aligned}
& \Rightarrow \frac{100}{9}=0+a(600) \\
& \Rightarrow a=\frac{100}{9 \times 600}=\frac{1}{6 \times 9} \\
& \Rightarrow a=\frac{1}{54}=0.0185 \mathrm{~ms}^{-2}
\end{aligned}
$
Therefore, the acceleration of the train is $0.0185 \mathrm{~ms}^{-2}$
Topic 7.4 Graphical Representation of Motion
Q 1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Answer:
A distance-time graph is the plot of the distance travelled by an object along the x-axis against time along the y-axis.
For the uniform motion of an object, the distance-time graph is a straight line with a constant slope.
For non-uniform motion of an object, the distance-time graph is a curved line with an increasing or decreasing slope.
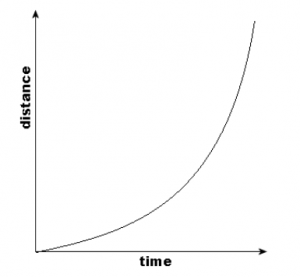
Answer:
If the distance-time graph of an object is a straight line parallel to the time axis, it means that the distance of the object is the same from its initial position at any point in time. This implies that the object is not moving and is at rest.
Answer:
If the speed-time graph of an object is a straight line parallel to the time axis, it means that the speed of the object is not changing with time. Hence, the speed of the object is constant. This also implies that the acceleration of the object is zero.
Q4. What is the quantity which is measured by the area occupied below the velocity-time graph?
Answer:
The area occupied below the velocity-time graph denotes the total distance travelled by an object in the given time frame.
We know,
Speed $=\frac{\text { Distance }}{\text { Time }} \Rightarrow$ Distance $=$ Speed $\times$ Time
Topic 7.5 Equations of motion by graphical method
Answer:
Given that the bus starts from rest. Hence, the initial speed of the bus $=0 m s^{-1}$
Acceleration of the bus, $a=0.1 m s^{-2}$
Time is taken, $t=2 \mathrm{~min}=2 \times 60 \mathrm{~s}=120 \mathrm{~s}$
(a) We know, $v=u+a t$
$
\Rightarrow v=0+(0.1)(120)=12 m s^{-1}
$
Therefore, the speed acquired by the bus is $12 \mathrm{~ms}^{-1}$
Answer:
Given that the bus starts from rest. Hence, the initial speed of the bus, $\mathrm{u}=0 \mathrm{~ms}^{-1}$
Acceleration of the bus, $a=0.1 m s^{-2}$
Time taken, $t=2 \mathrm{~min}=2 \times 60 \mathrm{~s}=120 \mathrm{~s}$
(b) We know, $s=u t+\frac{1}{2} a t^2$
$
\begin{aligned}
& \Rightarrow s=0(120)+\frac{1}{2}(0.1)(120)^2 \\
& \Rightarrow s=\frac{1}{2}(0.1)(14400) \\
& \Rightarrow s=720 \mathrm{~m}
\end{aligned}
$
Therefore, the distance travelled by bus is 720 m
Answer:
(We know, $1 \mathrm{~km}=1000 \mathrm{~m} ; 1 \mathrm{hr}=3600 \mathrm{~s}$ )
Given, Initial speed of the train, $u=90 \mathrm{kmh}^{-1}=\frac{90 \times 1000}{3600}=25 \mathrm{~ms}^{-1}$
Acceleration of the train, $a=-0.5 m s^{-2}$ (Negative sign implies retardation)
Since the train has to be brought to rest, the final speed of the train, $v=0 m s^{-1}$
We know, $v^2=u^2+2 a s$
$
\begin{aligned}
& \Rightarrow 0^2=25^2+2(-0.5) s \\
& \Rightarrow 0=625-s \\
& \Rightarrow s=625 m
\end{aligned}
$
Therefore, the train travels a distance of $625 m$ before coming to rest.
Answer:
Given that the trolley starts from rest. Hence, the initial speed of the trolley, $u=0 c m s^{-1}$
Acceleration of the trolley, $a=2 c m s^{-2}$
Time is taken, $t=3 s$
We know, $v=u+a t$
$
\Rightarrow v=0+(2)(3)=6 c m s^{-1}
$
Therefore, the velocity of the trolley after 3 sec is $6 \mathrm{cms}^{-1}$
Answer:
Given, Initial speed of the racing car, $\mathrm{u}=0 m s^{-1}$
Acceleration of the car, $a=4 m s^{-2}$
Time taken, $t=10 \mathrm{~s}$
We know, $s=u t+\frac{1}{2} a t^2$
$
\begin{aligned}
& \Rightarrow s=0(10)+\frac{1}{2}(4)(10)^2 \\
& \Rightarrow s=2(100) \Rightarrow s=200 m
\end{aligned}
$
Therefore, the distance travelled by the racing car in $10 s$ is $200 m$
Answer:
Taking upward direction as positive (+) direction:
Given,
$
u=5 m s^{-1}
$
$a=-10 \mathrm{~ms}^{-2}$ (This is due to gravitational force!)
The stone will move up until its velocity becomes zero.
$
\therefore v=0 m s^{-1}
$
We know, $v^2=u^2+2 a s$
$
\begin{aligned}
& \Rightarrow 0^2=5^2+2(-10) s \\
& \Rightarrow 20 s=25 \Rightarrow s=1.25 \mathrm{~m}
\end{aligned}
$
Therefore, the stone reaches a height of $1.25 m$
Now,
We know, $v=u+a t$
$
\Rightarrow 0=5+(-10) t \Rightarrow t=0.5 \mathrm{~s}
$
Therefore, the time taken by the stone to reach the maximum height is $0.5 s$.
NCERT Solutions for Class 9 Science Chapter 7 Motion: Solved Exercise Questions
The Class 9 Science Chapter 7 - Motion question answers provide well-articulated answers to all the end-of-chapter questions, expressing the key ideas of distance, speed, displacement, velocity, and acceleration. The solutions serve as the means of effective practice and foundation in solving problems on the basis of physics.
Answer:
Given, Diameter of the circular track $=200 \mathrm{~m}$
$\therefore$ The circumference of the circular track, $d=2 \pi \frac{D}{2}=200 \pi m$
The athlete completes one round of a circular track in 40 s.
$\therefore$ Speed of the athlete $=u=\frac{200 \pi m}{40 s}=5 \pi m s^{-1}$
In $t=2 \min 20 s=140 s$,
Distance travelled by the athlete $=$ Speed $\times$ time $=(5 \pi) \times(140)$
$
=5 \times \frac{22}{7} \times 140=2200 \mathrm{~m}
$
Also, the number of rounds the athlete will complete in $140 s=\frac{140}{40}=3.5$
Therefore, the final position of the athlete after $140 s$ will be diametrically opposite to his initial point.
( 3 complete rounds and one half round.)
Hence, displacement of the athlete = magnitude of the diameter of the circle =200m
Answer:
Given,
(a) Distance between A and $\mathrm{B}=300 \mathrm{~m}$
Time taken to reach from A to $\mathrm{B}=2 \min 30 s=150 s$
$\therefore$ Average speed from A to $\mathrm{B}=\frac{\text { Distance }}{\text { Time }}=\frac{300}{150}=2 \mathrm{~ms}^{-1}$
And, Average velocity from A to B $=\frac{\text { Displacement }}{\text { Time }}=\frac{300}{150}=2 m s^{-1}$
(In this case, average speed is equal to the average velocity)
(b) Distance travelled from A to reach C $=A B+B C=300+100=400 m$
And, Displacement from A to $\mathrm{C}=A C=300-100=200 \mathrm{~m}$
Also, time taken to reach C from $\mathrm{A}=2 \min 30 s+1 \min =(150+60) s=210 s$
$\therefore$ Average speed from A to C $=\frac{\text { Distance }}{\text { Time }}=\frac{400}{210}=1.90 \mathrm{~ms}^{-1}$
And, Average velocity from A to C $=\frac{\text { Displacement }}{\text { Time }}=\frac{200}{210}=0.95 \mathrm{~ms}^{-1}$
(In this case, average speed is not equal to the average velocity)
Answer:
Given, Average speed while going to school, $v_1=20 \mathrm{kmh}^{-1}$
And Average speed while returning back from school, $v_2=30 \mathrm{kmh}^{-1}$
Let the distance between the starting point and the school be $x m$
And the time taken by Abdul during the two trips be $t_1$ sandt ${ }_2 s$
We know, Speed $=\frac{\text { Distance }}{\text { Time }}$
$
\therefore v_1=\frac{x}{t_1}=20
$
And, $\therefore v_2=\frac{x}{t_2}=30$-(i)
Now, the Total distance that Abdul covers $=x+x=2 x$
And the total time Abdul takes to cover this distance is $=t_1+t_2$
$
\therefore v_{a v g}=\frac{2 x}{t_1+t_2}=\frac{2 x}{\frac{x}{20}+\frac{x}{30}}=\frac{60 \times 2 x}{5 x}=24 m s^{-1}
$
Therefore, the average speed for Abdul's trip is $24 \mathrm{~ms}^{-1}$
(Note: $\frac{20+30}{2}=25 m s^{-1} \neq 24 m s^{-1}$ )
Answer:
Given that the motorboat starts from rest. Hence, the initial speed of the motorboat, $\mathrm{u}=0 \mathrm{~ms}^{-1}$
Acceleration of the motorboat, $a=3.0 \mathrm{~ms}^{-2}$
Time taken, $t=8 s$
We know, $s=u t+\frac{1}{2} a t^2$
$
\begin{aligned}
& \Rightarrow s=0(8)+\frac{1}{2}(3)(8)^2 \\
& \Rightarrow s=\frac{1}{2}(3)(64) \\
& \Rightarrow s=96 m
\end{aligned}
$
Therefore, the distance travelled by the motorboat is 96 m
Answer:
The initial speed $=52 \times \frac{5}{18}=14.4 \frac{\mathrm{~m}}{\mathrm{~s}}$
After 5 sec, the car stops
The graph is represented by the blue line (x-axis is time and the y-axis is speed)
For the car with $3 \mathrm{kmh}^{-1}$. Initial speed $=3 \times \frac{5}{18}=0.833 \frac{\mathrm{~m}}{\mathrm{~s}}$. The graph, which is represented by the golden line
The initial speed $=52 \times \frac{5}{18}=14.4 \frac{\mathrm{~m}}{\mathrm{~s}}$
After 5 sec, the car stops
The graph is represented by the blue line ( x-axis is time and the y-axis is speed)
For the car with 3 km/h. Initial speed $=3 \times \frac{5}{18}=0.833 \frac{\mathrm{~m}}{\mathrm{~s}}$. The graph, which is represented by the golden line
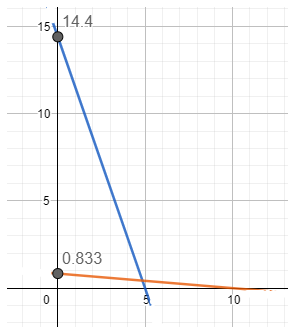
The area covered by the blue graph is greater than the golden graph, so the car with 15 m/s initial velocity travels la arge distance.
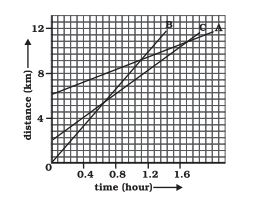
Which of the three is travelling the fastest?
Answer:
Given is a distance-time graph. The slope of this graph gives us speed. Hence, the graph with the highest slope will have the highest speed.
Since B has the highest slope(inclination), it travels the fastest.
Are all three ever at the same point on the road?
Answer:
Given is a distance-time graph. Any point on the curve will give the distance of the object from O. Since there is no intersection point of all three graphs, they never meet at the same point on the road.
(Although any two of them do meet at some point on the road!)
How far has C travelled when B passes A?
Answer:
Given is a distance-time graph. Any point on the curve will give the distance of the object from O. To find how far C has travelled when B passes A, draw a perpendicular from the intersection point of A and B on the time axis. The point where it intersects the C graph, from C, draw a perpendicular to the y-axis. Therefore, the distance travelled by C will be (Final distance from O - Initial distance from O)
Therefore, C has travelled 6.5 km when B passes A.
How far has B travelled by the time it passes C?
Answer:
Given is a distance-time graph. The graphs of B and C intersect at a point whose y-coordinate is 5. Hence, B has travelled 5km by the time it passes C.
Answer:
Considering the downward direction as the positive direction.
Given, Height from which the ball is dropped, $s=20 \mathrm{~m}$
Acceleration of the ball, $a=10 \mathrm{~ms}^{-2}$
Initial velocity, $u=0 m s^{-1}$
(i) We know, $v^2=u^2+2 a s$
$
\Rightarrow v^2=0^2+2(10)(20)
$
$\Rightarrow v^2=400$
$\Rightarrow v=20 m s^{-1}$ (In downward direction)
Therefore, the ball will strike the ground with a velocity of $20 \mathrm{~ms}^{-1}$
(ii) Now, we know, $v=u+a t$
$
\Rightarrow 20=0+10 t \Rightarrow t=2 s
$
Therefore, the ball reaches the ground in $2 s$.
Note: $v=-20 \mathrm{~ms}^{-1}$ was rejected because in this case, the negative sign implies the velocity in the upward direction, which is opposite to the direction of the motion of the ball(before collision).
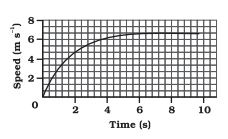
Q 8. (a) The speed-time graph for a car is shown in Figure:
Answer:
Given is a speed-time graph. The area under the curve will give the distance travelled by the car.
In time $t=4 s$, the distance travelled by the car will be equal to the area under the curve from $x=0$ to $x=4$
Considering this part of the graph as a quarter of a circle whose radius is $4$ units.
Therefore, required area $=\frac{1}{4} \pi r^2=\frac{1}{4} \pi(4)^2=12.56 \mathrm{~m}$
Therefore, the distance the car travelled in the first 4 seconds is 12.56 m
Q 8. (b) The speed-time graph for a car is shown in Figure:
Which part of the graph represents the uniform motion of the car?
Answer:
In uniform motion, the speed of the car will become constant, which is represented by a line parallel to the time axis. In the given figure, the straight line graph from t=6s to t=10s represents the uniform motion of the car.
Q 9. (a) State which of the following situations are possible and give an example for each of these: an object with a constant acceleration but with zero velocity
Answer:
(a) The given situation is possible.
When an object is thrown upwards (under gravity only), it reaches a maximum height where its velocity becomes zero. However, it still has an acceleration acting in the downward direction (acceleration due to gravity).
Note: This is possible for a given point in time; however, it is not possible for a period of time.
Q 9. (b) State which of the following situations are possible and give an example for each of these: an object moving with an acceleration but with uniform speed.
Answer:
(b) The given situation is possible.
An object moving in a circular path with uniform speed, i.e., covering equal distance in equal amount of time, is still under acceleration. Because the velocity keeps changing due to continuous change in the direction of motion. Therefore, circular motion is an example of an object moving with an acceleration but with uniform speed.
Q 9. (c) State which of the following situations are possible and give an example for each of these: an object moving in a certain direction with an acceleration in the perpendicular direction.
Answer:
(c) The given situation is possible.
For an object moving in a circular path with constant speed, the direction of its velocity at any point will be tangential to that point. However, its acceleration will be directed radially inwards. (Constant speed but still having an acceleration - Due to continuous change in direction.)
Answer:
Given, Radius of the circular orbit $=42250 \mathrm{~km}$
$
\therefore \text { Circumference of the orbit }=2 \pi r=2 \cdot \frac{22}{7} \cdot(42250)=265571 \cdot 4 \mathrm{~km}
$
The satellite takes 24 hours to revolve around the Earth.
We know, Speed $=\frac{\text { Distance }}{\text { Time }}$
$
\text { Speed }=\frac{265571.4}{24}=11065.4 \mathrm{kmh}^{-1}=\frac{11065.4}{3600} \mathrm{kms}^{-1}=3.07 \mathrm{kms}^{-1}
$
Therefore, the speed of the artificial satellite is $3.07 \mathrm{kms}^{-1}$
Class 10 Science NCERT Chapter 7: Higher Order Thinking Skills (HOTS) Questions
The HOTS questions in Chapter 7, Motion, provide challenges to students to use such concepts as displacement, velocity, acceleration, and representation of motion in graphs to solve complex problems in situations. Such questions develop analytical abilities and stimulate a better comprehension of real-life motion phenomena.
Q1:
The velocity-time graph of an object is shown in the figure. Identify the correct statement(s) regarding this graph.

(i)This is a non-uniform velocity-time graph of the object.
(ii) The velocity of the object is increasing at the same rate during OP and QR.
(iii) The velocity of the object is decreasing at the same rate during PQ and RT.
Answer:
From the graph, the velocity of the object is increasing at a constant rate for OP and QR and decreasing at a constant rate for PQ and RT. However, the rate of increasing or decreasing the velocity is not the same for all intervals. It is a non-uniform velocity-time graph.
Hence, the answer is option (1).
Q2:
A train is moving at a speed of 40 km/hr at 10:00 a.m., and at 50 km/hr at 10:02 a.m. Assuming that the train moves along a straight track and the acceleration is constant, find the value of the acceleration.
Answer:
$a =\frac{v-u}{t}=\frac{50 \mathrm{~km} / \mathrm{h}-40 \mathrm{~km} / \mathrm{h}}{2 \mathrm{~min}}$
$a=\frac{10 \mathrm{~km} / \mathrm{h}}{(3 / 20) \mathrm{h}}=\frac{10 \times 60}{2} \mathrm{~km} / \mathrm{h}^2=300 \mathrm{~km} / \mathrm{h}^2 $
$a =\frac{300 \times 1000}{3600 \times 3600} \mathrm{~m} / \mathrm{s}^2=0.02 \mathrm{~m} / \mathrm{s}^2$
Q3:
While driving through Napa, you observe a hot air balloon in the sky with tourists on board. One of the passengers accidentally drops a wine bottle, and you note that it takes 2.3 seconds for it to reach the ground. Find how high the balloon is.
Answer:
Given wine bottle is dropped, i.e.,u=0
$\begin{gathered}\Delta x=u t+\frac{1}{2} a t^2 \text { or } h=u t+\frac{1}{2} g t^2 \\ \mathrm{~h}=0+\frac{1}{2}\left(10 \mathrm{~m} / \mathrm{s}^2\right)(2.3 \mathrm{~s})^2=26.5 \mathrm{~m}\end{gathered}$
Q4:
A person starts jogging on a circular track and completes 5 full rounds. The circumference of the circular track is 88 m. Then find the net velocity of that person.
Answer:
Since the net displacement is zero, the net velocity will be zero.
Q5:
A bus covers a distance of 250 km from Delhi to Jaipur towards the West in 5 hours in the morning and returns to Delhi in the evening covering the same distance of 250 km in the same time of 5 hours. Find (a) the average speed, and ( b ) the average velocity, of the bus for the whole journey.
Answer:
(a)
$\begin{aligned} & \text { Average speed } \quad=\frac{\text { Total distance travelled }}{\text { Total time taken }} \\ = & \frac{250 \mathrm{~km}+250 \mathrm{~km}}{5 \mathrm{~h}+5 \mathrm{~h}} \\ = & \frac{500 \mathrm{~km}}{10 \mathrm{~h}}=50 \mathrm{~km} / \mathrm{h}\end{aligned}$
(b) In this case, the bus travels 250 km from Della to Jaipur towards the West and then comes back to the starting point, Delhi, in the reverse direction. So, the total displacement (or total distance travelled in a specified direction) will be 250 km-250 km=0
$\begin{aligned} & \text { Average velocity }=\frac{\text { Total displacement }}{\text { Total time taken }} \\ & =\frac{250 \mathrm{~km}-250 \mathrm{~km}}{5 \mathrm{~h}+5 \mathrm{~h}} \\ & \quad=\frac{0 \mathrm{~km}}{10 \mathrm{~h}} \\ & \quad=0 \mathrm{~km} / \mathrm{h}\end{aligned}$
Q6:
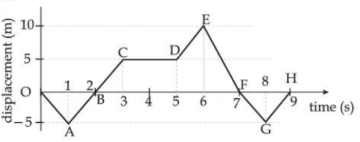
The displacement $x$ versus time graph is shown below.
(A) The average velocity during 0 to 3 s is $10 \mathrm{~m} / \mathrm{s}$
(B) The average velocity during 3 to 5 s is $0 \mathrm{~m} / \mathrm{s}$
(C) The instantaneous velocity at $\mathrm{t}=2 \mathrm{~s}$ is $5 \mathrm{~m} / \mathrm{s}$
(D) The average velocity during 5 to 7 s and the instantaneous velocity at $\mathrm{t}=6.5 \mathrm{~s}$ are equal
(E) The average velocity from $t=0$ to $t=9 \mathrm{~s}$ is zero
Choose the correct answer from the options given below
1. (B), (D), (E) only
2. (B), (C), (D) only
3. (A), (D), (E) only
4. (B), (C), (E) only
Answer:
$\begin{aligned}
& \langle\overline{\mathrm{v}}\rangle_{0-3}=\frac{5-0}{3}=5 / 3 \mathrm{~m} / \mathrm{s} \\
& \langle\overline{\mathrm{v}}\rangle_{3-5}=0 \\
& \overline{\mathrm{v}}_{\mathrm{t}-2}=5 \mathrm{~m} / \mathrm{s} \\
& \langle\overline{\mathrm{v}}\rangle_{5-7}=\frac{0-5}{2}=-2.5 \mathrm{~m} / \mathrm{s} \\
& \overline{\mathrm{v}}_{6-5}=-10 \mathrm{~m} / \mathrm{s} \\
& \langle\overline{\mathrm{v}}\rangle_{0-9}=0
\end{aligned}$
From $t=5$ to $t=7 \mathrm{sec}$ slope is not constant, so avg velocity is not equal to the instantaneous velocity.
Hence, the answer is option (4).
Q7:
A person travelling on a straight line moves with a uniform velocity $\mathrm{v}_1$ for a distance x and with a uniform velocity $\mathrm{v}_2$ for the next $\frac{3}{2} \mathrm{x}$ distance. The average velocity in this motion is $\frac{50}{7} \mathrm{~m} / \mathrm{s}$. If $\mathrm{v}_1$ is $5 \mathrm{~m} / \mathrm{s}$ then $\mathrm{v}_2=$ _____ $\mathrm{m} / \mathrm{s}$.
Answer:
$
\begin{aligned}
& \mathrm{v}_{\mathrm{avg}}=\frac{\mathrm{x}_1+\mathrm{x}_2}{\mathrm{t}_1+\mathrm{t}_2} \\
& \Rightarrow \frac{50}{7}=\frac{\mathrm{x}+\frac{3 \mathrm{x}}{2}}{\frac{\mathrm{x}}{5}+\frac{3 \mathrm{x}}{2 \mathrm{v}_2}} \\
& \Rightarrow \frac{50}{7}=\frac{5 / 2}{\frac{1}{5}+\frac{3}{2 \mathrm{v}_2}} \\
& \Rightarrow \frac{1}{5}+\frac{3}{2 \mathrm{v}_2}=\frac{7}{20} \\
& \Rightarrow \frac{3}{2 \mathrm{v}_2}=\frac{7}{20}-\frac{1}{5}=\frac{7-4}{20} \\
& \Rightarrow \frac{3}{2 \mathrm{v}_2}=\frac{3}{20} \\
& \Rightarrow \mathrm{v}_2=10 \mathrm{~m} / \mathrm{s}
\end{aligned}
$
Hence, the answer is 10.
NCERT Solutions for Class 9 Science Chapter 7 Motion - Key Topics
Motion Class 9 question answers cover all the key topics that explain how objects move, including concepts like speed, velocity, acceleration, and graphical representation of motion. These topics help students understand the fundamental laws that govern motion in everyday life.
7.1 Describing Motion
7.1.1 Motion along a straight line
7.1.2 Uniform Motion and Nonuniform Motion
7.2 Measuring the rate of motion
7.2.1 Speed with Direction
7.3 Rate of Change of Velocity
7.4 Graphical Representation of Motion
7.4.1 Distance- Time Graphs
7.4.2 Velocity-Time Graphs
7.5 Equations of Motion by Graphical Method
7.5.1 Equation for Velocity-Time Relation
7.5.3 Equation for Position-Velocity Relation
NCERT Solutions for Class 9 Science Chapter 7 Motion - Important Formulas
Motion important formulas in Class 9 Science are a rapid guide to the solutions of numerical problems concerning distance, displacement, speed, velocity, acceleration, and equations of motion. The formulas guide students to enhance their problem-solving capabilities as well as effectively prepare them to sit exams.
1. Speed
Speed $=\frac{\text { Distance }}{\text { Time }}$
2. Velocity
Velocity $=\frac{\text { Displacement }}{\text { Time }}$
3. Acceleration
$
\text { Acceleration }=\frac{\text { Change in velocity }}{\text { Time }}=\frac{v-u}{t}
$
Where:
$v=$ final velocity
$u=$ initial velocity
$t=$ time taken
Unit: $\mathrm{m} / \mathrm{s}^2$
4. Uniform Acceleration Equations of Motion
1. $v=u+a t$
2. $s=u t+\frac{1}{2} a t^2$
3. $v^2=u^2+2 a s$
Where:
$s=$ displacement
$a=$ acceleration
5. Average Speed
Average Speed $=\frac{\text { Total Distance }}{\text { Total Time }}$
Approach to Solve Questions of Class 9 NCERT Chapter 7: Motion
The approach to Solve Questions of Class 9 Science Chapter 7 -Motion is used to guide students to have a clear system and structure to solve the theoretical and numerical problems in the chapter. Students will be able to reinforce their knowledge by paying attention to the main terms, such as speed, velocity, acceleration, distance, and displacement, to answer questions correctly. This strategy will help learners relate real-life observations to what they learn in the textbook, which makes it easier and more effective to prepare for exams.
-
Read the question in order to know the quantities provided (such as distance, time, or the type of motion).
-
Determine the nature of the motion involved; is it non-uniform or uniform (with a steady speed)
-
Understand what is asked, i.e. which speed, in which direction, which distance is covered or which comparison of two motions.
-
Apply conceptual knowledge: apply the purpose of the question to definitions of motion, such as the distinction between speed and velocity.
-
It is also important to draw diagrams or motion graphs (as appropriate) to make the problem easier to understand.
-
Write down and organise the information in a step-by-step kind of representation before one tries the solution.
-
Break down units and directions. Units and directions are important to analyse, especially when it comes to displacement and velocity.
Benefits of NCERT Solutions for Class 9 Science Chapter 7 Motion
Advantages of NCERT Solutions for Class 9 Science Chapter 7 - Motion are that it assists the student to acquire the basic concepts of motion easily. These resources are interactive and less stressful since they provide detailed explanations, solved examples and step-by-step solutions. They also facilitate frequent revision, develop knowledge of numerical problems, and build confidence in both school examinations and competitive examinations.
- Clear Concept Understanding- The solutions are written in a clear and well-organised way that can make the learner understand motions, distance, displacement, speed, velocity and acceleration.
- Step-by-Step Solutions- The numerical problems are solved step-by-step, enabling the students to easily learn formulas and approaches.
- Exam-Oriented Preparation: Relevant exercises, QMCs and solved examples assist the students to be well prepared to face the board examination and competitive exams.
- Enhances Problem-Solving Skills -Different kinds of problems practised enhance such skills of analysis and application.
- Time-Saving Material- Ready-to-use solutions enable effective time management and quick revision of the study material during examination preparation.
- Supports Self-Learning – Students can use these solutions for self-study without much external guidance.
What You Will Learn from NCERT Solutions for Class 9 Science Chapter 7: Motion?
Students in this chapter get a clear-cut concept of motion and how it is explained in scientific terms and mathematical equations. As mentioned by referring to the Class 9 Science chapter 7 Motion solutions, the students will gain the following important concepts:
- This chapter makes the students aware of what motion is and how the position of a given object varies with time in terms of a reference point.
- Students get to know the various forms of motion, including uniform and non-uniform motion, as well as their features.
- With these Motion Class 9 question answers, students have a good grasp of key concepts such as distance, displacement, speed, velocity, and acceleration.
- The chapter is very clear in explaining the relationship between speed, velocity, acceleration, and time using equations of motion and graphical representations.
- Another aspect that students are educated on is the interpretation and drawing of distance-time and velocity-time graphs to explain how to analyse the motion of objects.
NCERT Solutions for Class 9 Science Chapter-wise
The chapter-wise NCERT Solutions for Class 9 Science provide detailed and accurate answers to all in-text and exercise questions. These solutions are designed as per the latest NCERT guidelines, helping students understand concepts clearly, practice effectively, and score well in exams.
NCERT Solutions for Class 9 - Subject Wise
NCERT Solutions for Class 9 provide clear, accurate, and well-structured answers to all textbook questions across subjects. These subject links enable the students to find the answers easily in all the chapters of the subject, enhance their ideas and study well to face the school exams and competitive tests.
Also, read,
NCERT Books and NCERT Syllabus
The CBSE curriculum is based on NCERT Books and NCERT Syllabus, which are fundamental to concept-based learning. These links are easy to access so that students are aware of the course structure required, adhere to the correct textbooks and study systematically to take exams.
Frequently Asked Questions (FAQs)
Distance is the total path covered (scalar), while displacement is the shortest path from start to end (vector).
Distance is the total path covered (scalar), while displacement is the shortest path from start to end (vector).
When an object covers equal distances in equal time intervals.
Read the question carefully to identify the type of motion (rectilinear, circular, etc.). For numerical questions, use the formula Speed = Distance ÷ Time, and ensure units are correct. For descriptive questions, name the motion and give a real-life example.
Understanding motion helps us describe how objects move, predict their positions, and apply these concepts in transportation, sports, machines, and more.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters