Gravitation Class 9th Notes - Free NCERT Class 9 Science Chapter 10 Notes - Download PDF

NCERT notes Class 9 Science Chapter 9 Gravitation: Download PDF

The Class 9 Science Chapter 9 Gravitation Notes provide a brief and properly organised material to assist the students in revising one of the most crucial chapters of physics with minimal effort. These Class 9 Science Chapter 9 Gravitation Notes are developed according to the newest CBSE syllabus and, therefore, simplify the essential concepts of gravity, free fall, buoyancy, and pressure in fluids. They facilitate revision because they are well-explained using formulas and diagrams that are easier to understand. The PDF can be easily downloaded by the students to understand their knowledge and achieve higher grades in exams.

Download PDF

NCERT notes Class 9 Science Chapter 9 Gravitation

The Gravitation Class 9 Science Chapter 9 CBSE notes give a concise and simple summary of all the major concepts associated with gravity and its impact. These Gravitation Class 9 Science Chapter 9 CBSE notes are prepared by the subject professionals according to the latest CBSE syllabus and can assist the students in revising some critical topics in a quick and effective way. They are well organised, have explanations, formulas, and diagrams that make the learning experience more efficient. These are notes that are perfect for preparing exams and developing good conceptual clarity.

Gravitation

Gravitation is the force of attraction between any two objects in the universe. It was first explained by Sir Isaac Newton

Newton's Observations

• Apple falls on the ground because the earth attracts it towards itself.

• Can Apple also attract the Earth? - Yes. Apple also attracts the Earth as per Newton's third law. But the mass of the Earth is extremely larger than Apple's mass, hence, the force applied by Apple is negligible and Earth never moves towards it.

• Newton then suggested that every object in this universe attracts another object. This force of attraction is called the Gravitational Force.

Universal Law of Gravitation

Newton proposed a law that we call Newton's law of Gravitation. According to this law. "Every particle in the universe attracts every other particle with a force, which is directly proportional to the product of their masses and inversely proportional to the square of the distance between the two masses. The direction of force is along the line joining the two particles."

Consider two particles $A$ and $B$ of masses $m_1$ and $m_2$ respectively separated by a distance $r$ as shown in the figure.

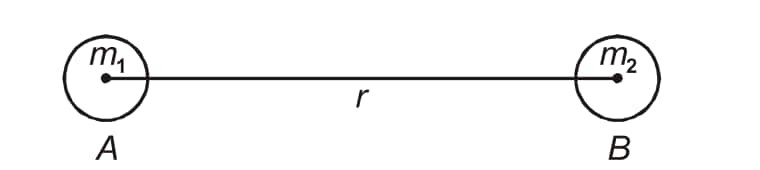
If $F$ is the force of attraction between $A$ and $B$, then

$
\begin{aligned}
& F \propto m_1 \times m_2 -----(i)\\
& F \propto \frac{1}{r^2}-----(ii)
\end{aligned}
$
Combining (i) and (ii), we get

$
\begin{aligned}
& F \propto \frac{m_1 m_2}{r^2} \\
& F=\frac{G m_1 m_2}{r^2}
\end{aligned}
$

where $G$ is the constant of proportionality called the universal gravitational constant.

$
G=\frac{F r^2}{m_1 m_2}
$

The SI unit of universal gravitational constant is $\frac{\mathrm{Nm}^2}{\mathrm{~kg}^2}$ and its numerical value is found to be,

$
G=6.67 \times 10^{-11} \mathrm{Nm}^2 / \mathrm{kg}^2
$

This force between any two particles is not altered by the other objects, even if they are located between the particles.

Properties of Gravitational Force

1. It is independent of the medium between the particles.
2. It is always attractive in nature.
3. It is the weakest force in nature.
4. It is a conservative force, i.e., the work done by it on a particle doesn't depend on the path taken by the particle; or the work done in moving a particle around a closed path under the action of gravitational force is zero.
5. The magnitude of force with which one body (say the earth) attracts the second body (say an apple) is equal to the magnitude of force with which the second body (say the apple) attracts the first body (in accordance with Newton $3^{\text {rd }}$ law).
6. It is a two-body interaction, i.e., the gravitational force between two particles is independent of the presence or absence of other particles.
7. It is a central force, i.e., acts along the line joining the two particles or centres of the interacting bodies.

Applications of Newton's Law of Gravitation

The following are the applications of Newton's law of gravitation :
1. It helps us to determine the mass of the Earth, the sun, the moon and the planets.
2. To determine the motion of the moon around the Earth.
3. To describe the motion of planets around the sun.
4. To describe the tides due to the moon and the sun.
5. To estimate the mass of the double stars.
6. It helps us to discover new stars and planets.

Importance of the Universal Law of Gravitation

The universal law of gravitation successfully explained several phenomena which were believed to be unconnected:

(i) the force that binds us to the earth;
(ii) the motion of the moon around the Earth;
(iii) the motion of planets around the Sun; and
(iv) the tides due to the moon and the Sun.

Free Fall

When an object falls towards the earth because of the earth’s gravity and there is no other force acting upon it, the object is in a free-fall state. Air resistance is negligible.

The value of ‘g' is the same on the Earth; thus, the equations of motion for an object with uniform motion are valid.

$\begin{aligned} & v=u+g t \\ & s=u t+g t^2 / 2 \\ & 2 g s=v^2-u^2\end{aligned}$

To calculate the Value of g

To calculate the value of $g$, we should put the values of G, $M$ and $R$ in Eq. (9.9), namely, universal gravitational constant, $\mathrm{G}=6.7 \times 10^{-11}$ $\mathrm{N} \mathrm{m}^2 \mathrm{~kg}^{-2}$, mass of the earth, $M=6 \times 10^{24} \mathrm{~kg}$, and radius of the earth, $R=6.4 \times 10^6 \mathrm{~m}$.

$
\begin{aligned}
g & =\mathrm{G} \frac{M}{R^2} \\
& =\frac{6.7 \times 10^{-11} \mathrm{~N} \mathrm{~m}^2 \mathrm{~kg}^{-2} \times 6 \times 10^{24} \mathrm{~kg}}{\left(6.4 \times 10^6 \mathrm{~m}\right)^2} \\
& =9.8 \mathrm{~m} \mathrm{~s}^{-2}
\end{aligned}
$

Thus, the value of acceleration due to gravity of the earth, $g=9.8 \mathrm{~m} \mathrm{~s}^{-2}$.

Motion of Objects Under the Influence of the Gravitational Force of the Earth

In the case of free fall, the acceleration of the body is uniform, which is independent of the mass of the body. Therefore, all the equations of uniformly accelerated motion of the bodies become valid with acceleration ' $a$ ' replaced by ' $g$ '.
$v=u+g t \quad(a$ replaced by $g$ in $v=u+a t)$
$h=u t+\frac{1}{2} g t^2 \quad\left(s\right.$ replaced by $h$ and $a$ replaced by $g$ in $\left.s=u t+\frac{1}{2} a t^2\right)$
$v^2=u^2+2 g h \quad\left(s\right.$ replaced by $h$ and a replaced by $g$ in $\left.v^2=u^2+2 a s\right)$

Mass

Mass: Mass of a body is the quantity of matter contained in it. It remains the same whether the object is on the Earth, the moon or anywhere in space. Thus, the mass of a body remains constant. The mass of a body is the measure of its inertia and hence, it is also known as inertial mass. It is a scalar quantity and cannot be negative. The SI unit of mass is the kilogram and is represented by (kg).

Weight

The weight of a body on Earth is the force with which it is attracted towards the centre of the Earth.
According to Newton's second law,

$
F=m a=\text { mass } \times \text { acceleration }
$

The acceleration produced by the gravitational force is known as the acceleration due to gravity (g).

$
\therefore \quad F=m g
$

By definition of weight, the force of attraction of the Earth on a body is the weight of the body on Earth. It is denoted by $W$.

So, $W=m g$
* The SI unit of weight is the same as the force, i.e., newton.

$
1 \mathrm{~N}=1 \mathrm{~kg} \mathrm{~m} / \mathrm{s}^2
$

* The weight is a force which acts vertically downward.
* It is a vector quantity. It has both magnitude and direction.

Weight of an Object on the Moon

The weight of an object depends on the gravitational force acting on it. Since the Moon's gravity is about one-sixth of Earth's gravity, an object will weigh six times less on the Moon than it does on Earth.

The formula for weight is:

$
\text { Weight }(\mathrm{W})=\text { mass }(\mathrm{m}) \times \text { acceleration due to gravity }(\mathrm{g})
$

On the Moon:

$
W_{\text {moon }}=m \times g_{\text {moon }}=m \times \frac{1}{6} g_{\text {earth }}
$

So, if an object weighs 60 N on Earth, it would weigh about 10 N on the Moon. However, its mass remains the same both on Earth and on the Moon.

Thrust and Pressure

The net force acting on an object perpendicular to its surface is called thrust. The normal force per unit area is called pressure.

Pressure: The thrust on unit area is called pressure.
Thus, Pressure $=\frac{\text { Thrust }}{\text { Area }}$
Pressure is a scalar quantity.
SI unit of Pressure: By putting the SI unit of thrust ( N ) and area ( $\mathrm{m}^2$ ) in the above relation, we get $\frac{\text { newton }}{\text { metre }^2}$ or $\frac{\mathrm{N}}{\mathrm{m}^2}$

Pressure in Fluids

Fluids (liquids and gases) exert pressure in all directions. The pressure at a point in a fluid increases with depth and depends on the density of the fluid and the gravitational force.

The formula for pressure in a fluid is:

$
\begin{gathered}
\text { Pressure }(\mathrm{P})=\operatorname{density}(\rho) \times \operatorname{gravitational~acceleration}(g) \times \text { height }(\mathrm{h}) \\
\qquad P=\rho g h
\end{gathered}
$

Buoyancy

Every fluid exerts an upward force on a body immersed in it. This upward force is called the buoyant force or buoyancy.

Buoyant force depends on:

• The volume of fluid displaced
• The density of the fluid

Formula (for buoyant force):

$
\text { Buoyant Force }=\rho \times g \times V
$

Why Objects Float or Sink When Placed on the Surface of Water?

A thing made of wood floats over the surface of water, but a small pin made of iron, when put on the surface of water, sinks to the bottom.

It can be understood by considering the number of forces acting on a body when it is immersed in a liquid.
When a body is immersed in a liquid, there are two forces acting on the body as given below
(i) The weight of the body acts vertically downward, which has a tendency to sink the body in the liquid due to gravity.
(ii) Upward thrust of the liquid acts vertically upward, which is equal to the weight of the liquid displaced by the immersed part of the body. This force has a tendency to push the body out of the given liquid.

How to Master Class 9 Science Chapter 9 Gravitation?

Class 9 Science Chapter 9: Gravitation is easy to master once you effectively have the logic behind the concepts of gravity, buoyancy, and motion under the force of gravity. This chapter is very conceptual; therefore, in order to score well, the emphasis has to be on real-life examples and practice. Through the proper strategy, you could understand your fundamentals and train adequately for school exams and competitive examinations of the future.

• Begin by reading the entire NCERT chapter in order to learn the meaning of gravitation, gravity, free fall and acceleration due to gravity.
• Become familiar with the Universal Law of Gravitation and practice the formula to get a better understanding of it.
• Learn the difference between mass and weight, and work on the numericals using the formula W = mg.
• Learn about buoyancy and the principle of Archimedes through examples of buoyancy in day-to-day lives, such as floating boats, balloons and ice in water.
• Memorise the significant equations like gravity, pressure, density and acceleration due to gravity.
• Solve all the numerical problems of the NCERT textbook, examples, textbook exercises, and exemplar questions.
• Draw and revise diagrams like free-body diagrams, force diagrams, and pressure illustrations to improve visual understanding.
• Practice past year questions and sample papers of CBSE to learn the pattern of the examination.
• Write brief notes with formulas, definitions and with most important points to revise before exams.
• In the revision, go through the chapter at least 2-3 times; the repetition of revision is also beneficial in memorising formulas and principles.

Importance of Class 9 Physics Chapter 9 Gravitation Notes

The Gravitation Class 9 Science Notes are very vital as they enable the students to learn one of the most basic forces of nature in a straightforward and systematised manner. These Gravitation Class 9 Science Notes simplify concepts such as gravity, free fall, buoyancy, mass, weight, and pressure in fluids into simplified explanations, and the concepts are far easier to remember. They contain significant formulas, drawings, and illustrations to help the students apply the topics in numerical and practical cases. These notes also come in handy to revise briefly before tests, because they point out all the exam-oriented points according to the recent CBSE syllabus. These notes facilitate the creation of sound conceptual clarity in the future since advanced physics topics in higher classes rely on the foundations of gravitation. They are also helpful in preparing competitive exams such as JEE, NEET, NTSE, Olympiads and similar, where basic physics knowledge is necessary. All in all, these notes help to study effectively, efficiently and in an organised manner so that people can score high in exams and reinforce their long-term knowledge.

NCERT Notes Class 9 Science Chapter-Wise

The Chapter-Wise NCERT Notes of Class 9 provide a concise and well-structured set of study materials for each of the chapters in the syllabus. These notes, prepared by experts in the subject, according to the most current guidelines of the CBSE, simplify the concepts with clear explanations, diagrams and main points. They are able to assist students in revising within a short time, build strengths, and prepare well to take exams. Chapter-by-chapter links allow students to navigate topics readily and learn in a well-organised and effective way.

NCERT Solutions Of Class 9 Subject-Wise

• NCERT solutions for class 9 Maths
• NCERT solutions for class 9 Science

NCERT Class 9 Exemplar Solutions for Other Subjects:

• NCERT Exemplar Class 9 Maths solutions
• NCERT Exemplar Class 9 Science solutions