NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3 - Triangles
A triangle is a closed figure that has three sides, three angles and three vertices. Two triangles can be compared based on their similarity, and in mathematics if two triangles are similar, then these two triangles are congruent to each other. Two triangles are said to be congruent if the corresponding sides and angles are equal. In the previous exercise, questions were solved using congruent properties of triangles like ASA, AAS, ASA. In this section two more congruent rules SSS (side - side - side) and RHS (right angle-hypotenuse-side). SSS congruent follows when all the corresponding sides of two triangles are equal. RHS follows when the hypotenuse and one side of the right angle triangle is equal to the hypotenuse and other side of another right triangle.
This Story also Contains
- NCERT Solutions for Class 9 Maths Chapter 7 – Triangles Exercise 7.3
- Access Triangles Class 9 Chapter 7 Exercise: 7.3
- Topics covered in Chapter 7 Triangles: Exercise 7.3
- NCERT Solutions of Class 9 Subject Wise
- Subject-Wise NCERT Exemplar Solutions

In this chapter of NCERT Solutions, we explore triangles and their properties, and Exercise 7.3 focuses on practical problem-solving using these concepts. Our free PDF 9th class maths exercise 7.3 answers break down complex concepts, making it easier for students to understand and practice. These resources are designed to help your learning and are accessible at your convenience. Whether you need to revise, prepare for exams, or strengthen your grasp of triangle properties, these NCERT class 9 maths chapter 7 exercise 7.3 solutions are here to assist you on your academic journey. Along with NCERT books Class 9 Maths, chapter 7, exercise 7.3, the following exercises are also present.
Access Triangles Class 9 Chapter 7 Exercise: 7.3
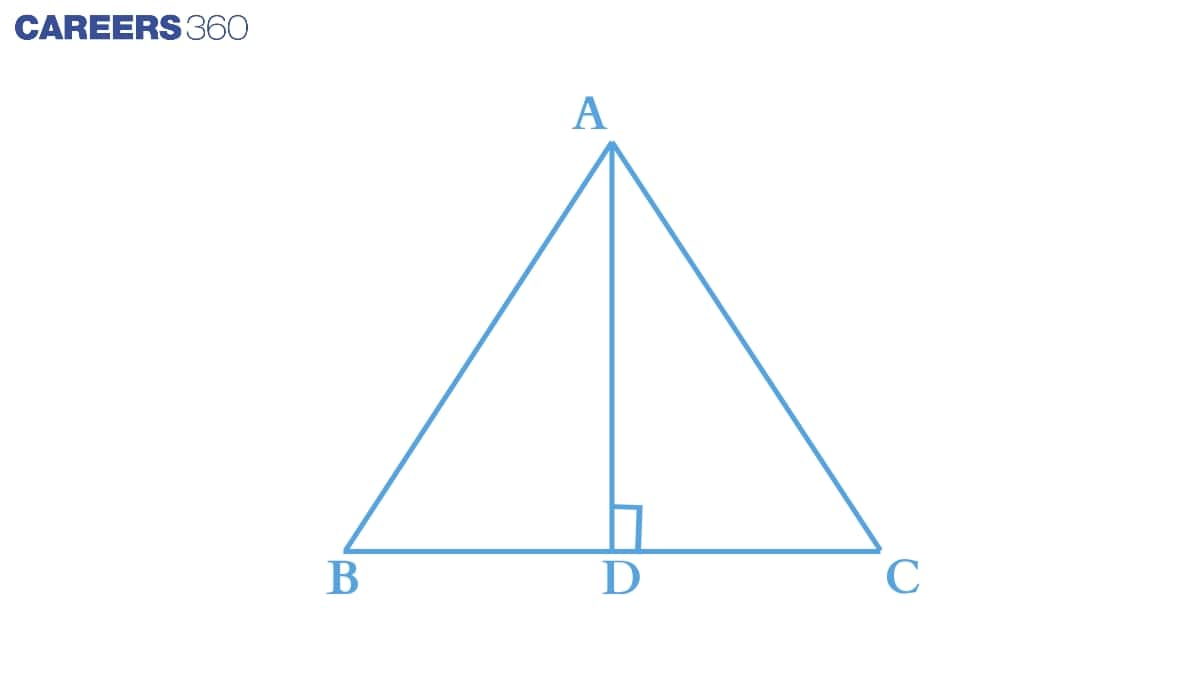
Answer:
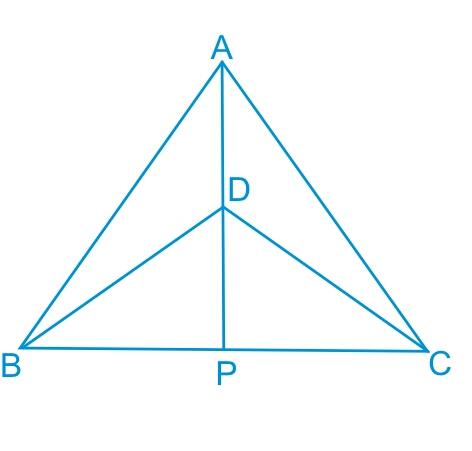
Consider ΔABD and ΔACD ,
(i) AD = AD (Common)
(ii) AB = AC (Isosceles triangle)
(iii) BD = CD (Isosceles triangle)
Thus by SSS congruency we can conclude that :
ΔABD≅ΔACD
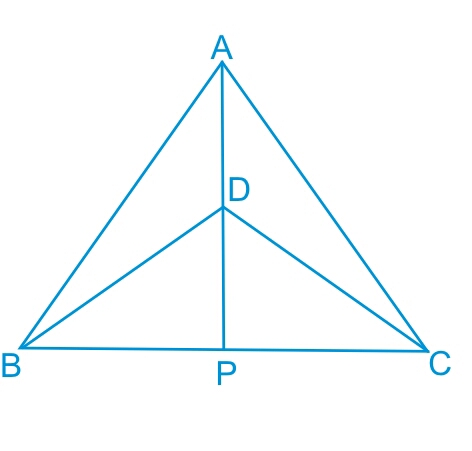
Answer:
Consider ΔABP and ΔACP ,
(i) AP is common side in both the triangles.
(ii) ∠PAB = ∠PAC (This is obtained from the c.p.c.t. as proved in the previous part.)
(iii) AB = AC (Isosceles triangles)
Thus by SAS axiom, we can conclude that :
ΔABP≅ΔACP
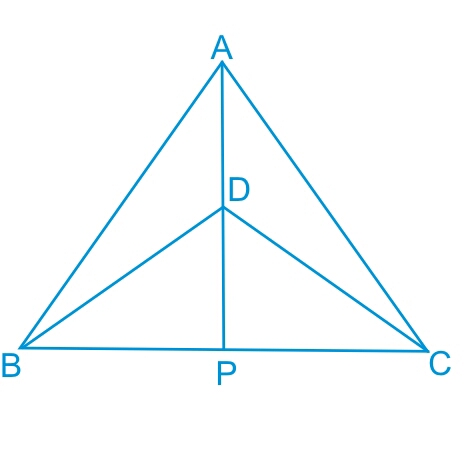
Answer:
In the first part, we have proved that ΔABD≅ΔACD .
So, by c.p.c.t. ∠PAB = ∠PAC .
Hence AP bisects ∠A .
Now consider ΔBPD and ΔCPD ,
(i) PD = PD (Common)
(ii) BD = CD (Isosceles triangle)
(iii) BP = CP (by c.p.c.t. from the part (b))
Thus by SSS congruency we have :
ΔBPD ≅ ΔCPD
Hence by c.p.c.t. we have : ∠BDP = ∠CDP
or AP bisects ∠D .
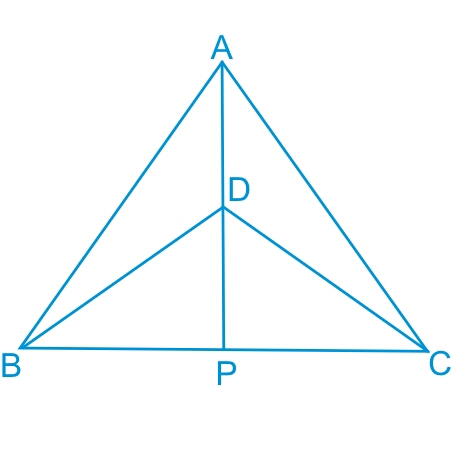
Answer:
In the previous part we have proved that ΔBPD ≅ ΔCPD .
Thus by c.p.c.t. we can say that : ∠BPD = ∠CPD
Also, BP = CP
SInce BC is a straight line, thus : ∠BPD + ∠CPD = 180∘
or 2∠BPD = 180∘
or ∠BPD = 90∘
Hence it is clear that AP is a perpendicular bisector of line BC.
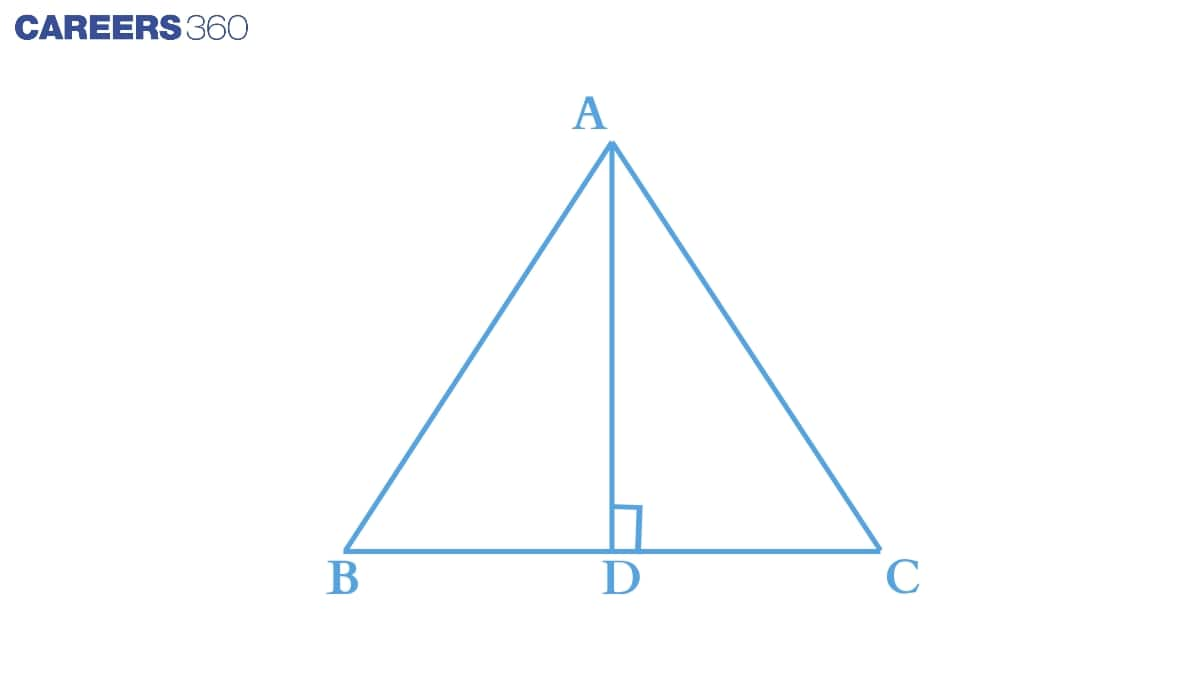
Q2 (i) AD is an altitude of an isosceles triangle ABC in which AB=AC . Show that AD bisects BC
Answer:
Consider ΔABD and ΔACD ,
(i) AB = AC (Given)
(ii) AD = AD (Common in both triangles)
(iii) ∠ADB = ∠ADC = 90∘
Thus by RHS axiom we can conclude that :
ΔABD ≅ ΔACD
Hence by c.p.c.t. we can say that : BD = CD or AD bisects BC.
Q2 (ii) AD is an altitude of an isosceles triangle ABC in which AB=AC . Show that AD bisects ∠A .
Answer:
In the previous part of the question we have proved that ΔABD ≅ ΔACD
Thus by c.p.c.t., we can write :
∠BAD = ∠CAD
Hence AD bisects ∠A .
Answer:
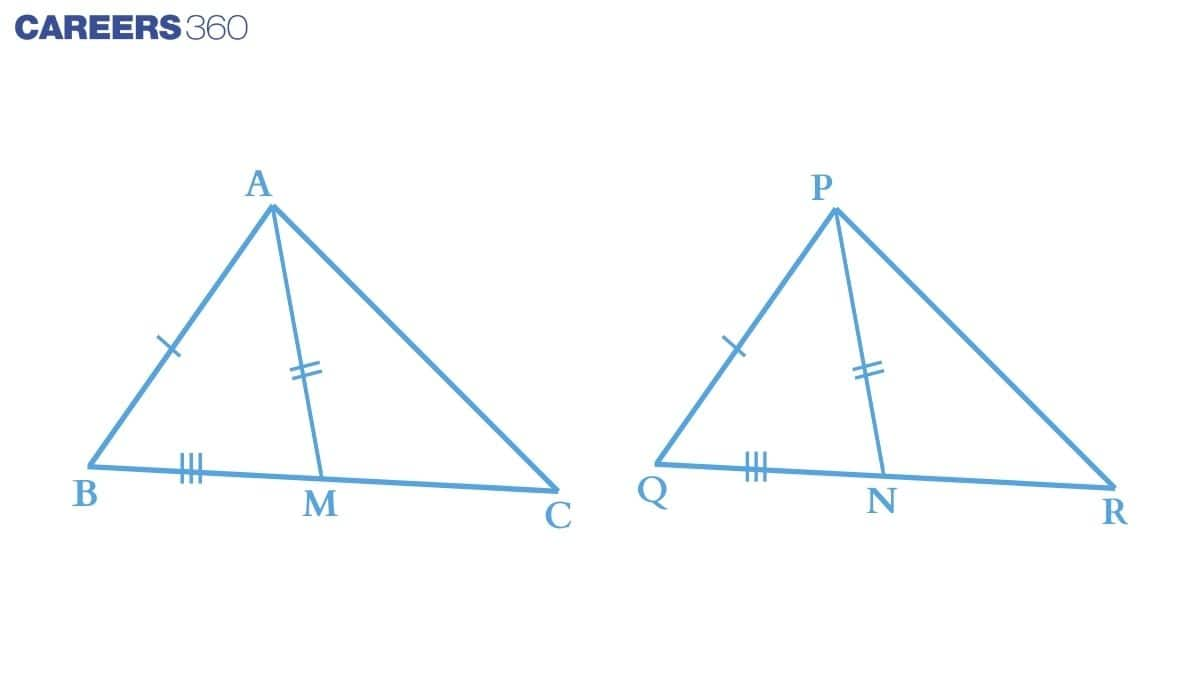
(i) From the figure we can say that :
BC = QR
or 12BC = 12QR
or BM = QN
Now, consider ΔABM and ΔPQN ,
(a) AM = PN (Given)
(b) AB = PQ (Given)
(c) BM = QN (Prove above)
Thus by SSS congruence rule, we can conclude that :
ΔABM≅ΔPQN
(ii) Consider ΔABC and ΔPQR :
(a) AB = PQ (Given)
(b) ∠ABC = ∠PQR (by c.p.c.t. from the above proof)
(c) BC = QR (Given)
Thus by SAS congruence rule,
ΔABC≅ΔPQR
Answer:
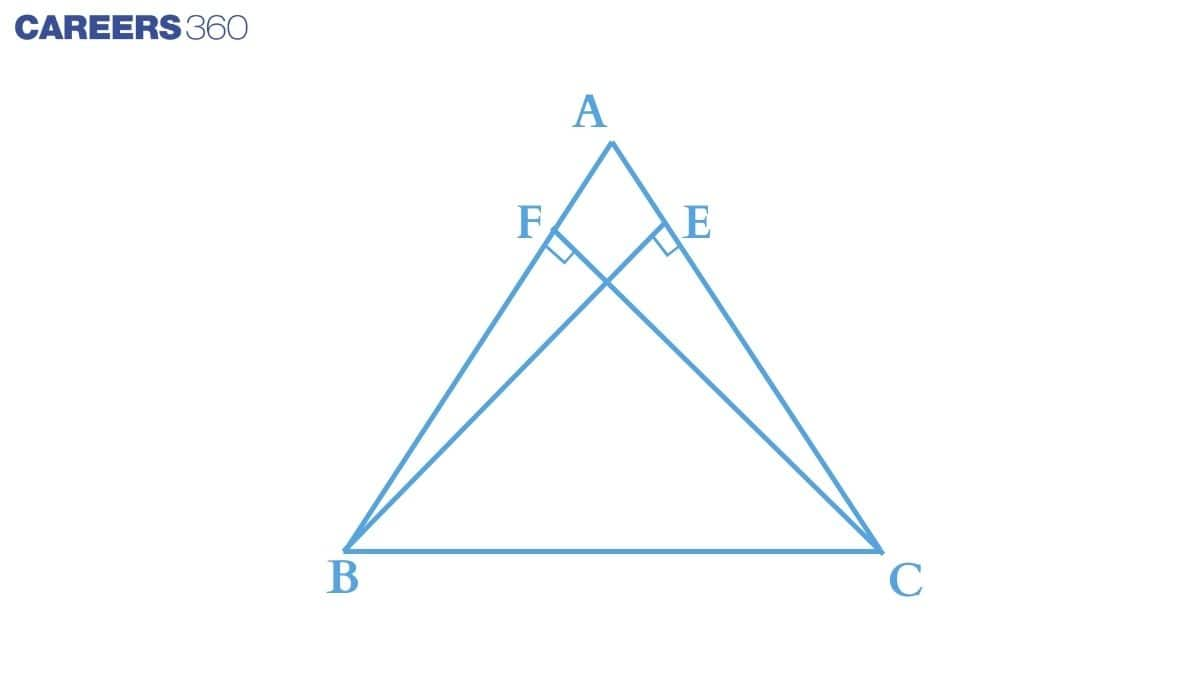
Using the given conditions, consider ΔBEC and ΔCFB ,
(i) ∠BEC = ∠CFB (Right angle)
(ii) BC = BC (Common in both the triangles)
(iii) BE = CF (Given that altitudes are of the same length. )
Thus by RHS axiom, we can say that : ΔBEC ≅ΔCFB
Hence by c.p.c.t., ∠B = ∠C
And thus AB = AC (sides opposite to equal angles are also equal). Thus ABC is an isosceles triangle.
Q5 ABC is an isosceles triangle with AB=AC . Draw AP⊥BC to show that ∠B=∠C .
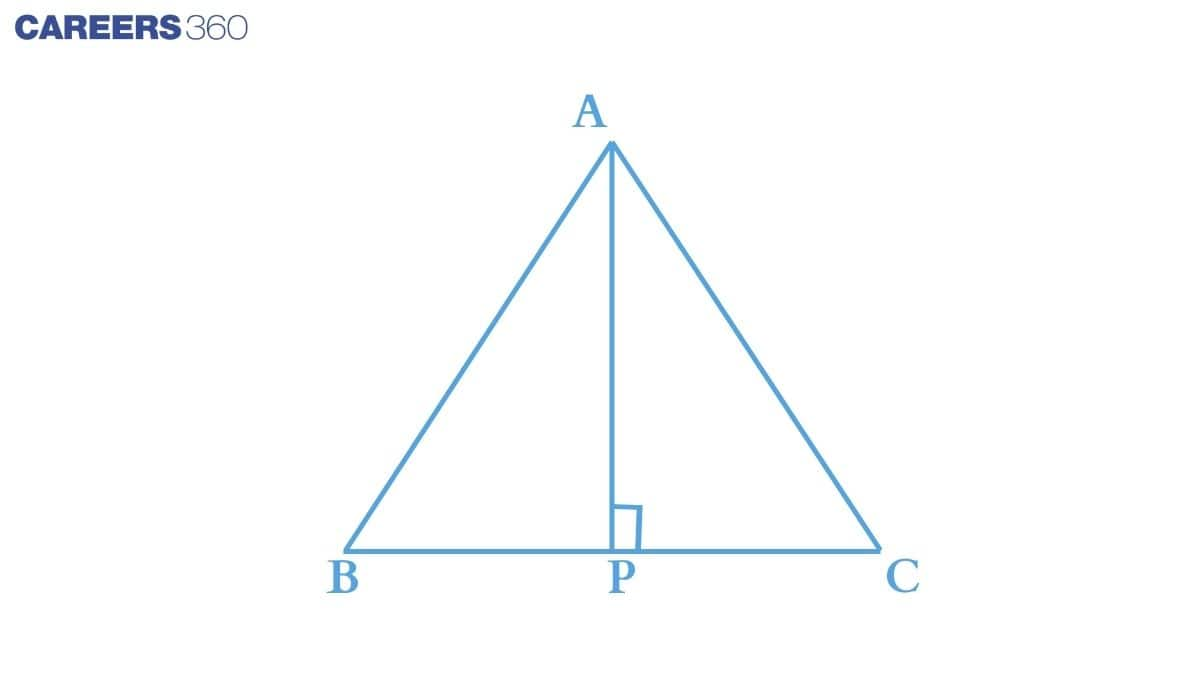
Answer:
Consider ΔABP and ΔACP ,
(i) ∠APB = ∠APC = 90∘ (Since it is given that AP is altitude.)
(ii) AB = AC (Isosceles triangle)
(iii) AP = AP (Common in both triangles)
Thus by RHS axiom we can conclude that :
ΔABP ≅ΔACP
Now, by c.p.c.t.we can say that :
∠B = ∠C
Also Read:
Topics covered in Chapter 7 Triangles: Exercise 7.3
- The SSS congruence principle expresses that if three sides of one triangle are equivalent to those of another triangle, the two triangles are congruent to one other.
- The RHS Congruence rule, expresses that two right triangles are congruent if the hypotenuse and one side of one triangle are equivalent to the hypotenuse and one side of the other triangle.
- A point that is equidistant from two given points is found on the perpendicular bisector of the line segment that connects them, and vice versa. On the bisectors of the angles formed by the two lines, a point equidistant from two intersecting lines lies.
Also See:
NCERT Solutions of Class 9 Subject Wise
Students must check the NCERT solutions for Class 9 Maths and Science given below:
Subject-Wise NCERT Exemplar Solutions
Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:
Frequently Asked Questions (FAQs)
No, these triangles are similar, not congruent.
The different types of triangles are:
Scalene Triangle.
Isosceles Triangle.
Equilateral Triangle.
No, an equilateral triangle can never be a right-angled triangle as each angle of an equilateral triangle is 60 degrees.
This exercise includes new methods of congruency of triangles like right-angle hypotenuse side, side-side- side theorem and some properties.
We are introduced to two new criteria of congruence:
The RHS (Right angle Hypotenuse Side) and the SSS (Side Side Side) congruence.
Two triangles are said to be congruent if all three corresponding sides of the two triangles are equal and all the three corresponding angles of the triangles are equal in measurement.
It expresses that if the hypotenuse and side of one right-calculated triangle are equivalent to the hypotenuse and the relating side of another right-angled triangle, then the two triangles are congruent.
It expresses that two triangles are congruent if three sides of a triangle are equivalent to the relating sides of the other triangle.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters