NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.2 - Triangles

Q1 (i) In an isosceles triangle ABC, with AB=AC , the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that : OB=OC

Answer:

Given, AB = AC, and ABC is an isosceles triangle.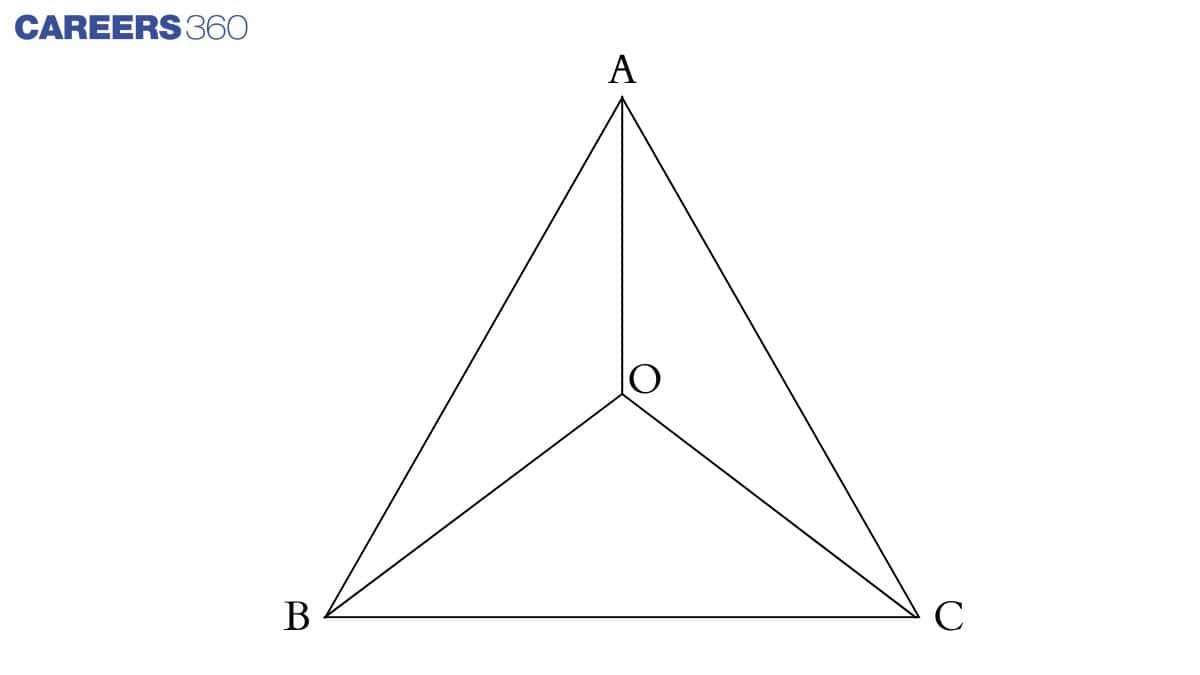

Therefore, it means ∠B=∠C

or 12∠B = 12∠C

Thus, ∠OBC = ∠OCB (Angles bisectors are equal)

Hence, OB=OC as sides opposite to equal are angles are also equal.

Q1 (ii) In an isosceles triangle ABC, with AB=AC , the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that : AO bisects ∠A

Answer:

Consider ΔAOB and ΔAOC ,

(i) AB = AC (Given)

(ii) AO = AO (Common in both the triangles)

(iii) OB = OC (Proved in previous part)

Therefore by SSS congruence rule, we can conclude that :

ΔAOB ≅ ΔAOC

Now, by c.p.c.t.,

∠BAO = ∠CAO

Hence AO bisects ∠A .

Q2 In ΔABC , AD is the perpendicular bisector of BC (see Fig). Show that ΔABC is an isosceles triangle in which AB=AC .

Answer:

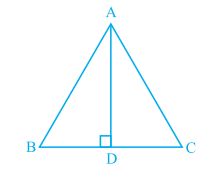
Given: AD is perpendicular bisector of BC.

To Prove: AB = AC

Proof: Consider Δ ABD and Δ ADC,

(i) AD = AD (Common in both the triangles)

(ii) ∠ADB = ∠ADC (Right angle)

(iii) BD = CD ( as AD is perpendicular to side BC)

Therefore, by SAS congruence criteria:

ΔADB ≅ ΔADC

Thus, AB = AC ( by c.p.c.t )

Hence Proved

Q3 ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig.). Show that these altitudes are equal.

Answer:

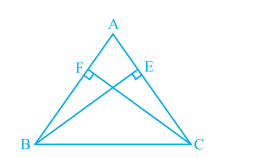
Given: AC = AB and BE and CF are altitudes.

To Prove: BE = CF

Proof: Consider ΔAEB and ΔAFC ,

(i) ∠A is common in both the triangles.

(ii) ∠AEB = ∠AFC (Right angles)

(iii) AB = AC (Given)

Thus by AAS congruence axiom, we can conclude that :

ΔAEB ≅ΔAFC

Now, by c.p.c.t. we can say : BE = CF

Hence Proved

Q4 (i) ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig). Show that ΔABE≅ΔACF

Answer:

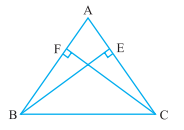
Given: BE = CF

Consider ΔABE and ΔACF ,

(i) ∠A is common in both the triangles.

(ii) ∠AEB = ∠AFC (Right angles)

(iii) BE = CF (Given)

Thus by AAS congruence, we can say that :

ΔABE≅ΔACF

Hence Proved

Q4 (ii) ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig.). Show that AB=AC , i.e., ABC is an isosceles triangle.

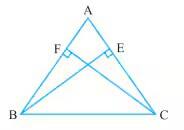
Answer:

From the prevoius part of the question we found out that : ΔABE ≅ΔACF

Now, by c.p.c.t. we can say that : AB = AC

Thus, Δ ABC is an isosceles triangle.

Hence Proved

Q5 ABC and DBC are two isosceles triangles on the same base BC (see Fig.). Show that ∠ABD =∠ACD.

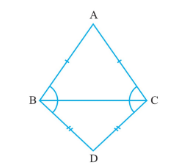
Answer:

Given: ABC and DBC are isosceles triangles and

To Prove: ∠ABD =∠ACD

Proof: Consider ΔABD and ΔACD,

(i) AD = AD (Common in both the triangles)

(ii) AB = AC (Sides of isosceles triangle)

(iii) BD = CD (Sides of isosceles triangle)

Thus by SSS congruency, we can conclude that:

△ABD ≅ triangleACD

Therefore, by c.p.c.t.,

∠ABD =∠ACD

Hence Proved

Q6 ΔABC is an isosceles triangle in which AB=AC . Side BA is produced to D such that AD=AB (see Fig.). Show that ∠BCD is a right angle.

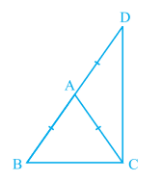
Answer:

Given: AB = AC and AD = AB

To Prove: ∠BCD is a right angle

Proof: Consider Δ ABC,
It is given that AB = AC
So, ∠ACB=∠ABC (Since angles opposite to the equal sides are equal.)

Similarly in Δ ACD, AD = AB and ∠ADC=∠ACD
So,

∠CAB+∠ACB+∠ABC=180∘

∠CAB + 2∠ACB=180∘
or ∠CAB =180∘ − 2∠ACB ...........................(i)

And in Δ ADC,
∠CAD =180∘ − 2∠ACD ..............................(ii)

Adding (i) and (ii), we get :
∠CAB + ∠CAD =360∘ − 2∠ACD − 2∠ACB

or 180∘ =360∘ − 2∠ACD − 2∠ACB

and ∠BCD = 90∘

Hence Proved

Q7 ABC is a right angled triangle in which ∠A=90∘ and AB=AC . Find ∠B and ∠C .

Answer:

Given: AB = AC and ∠A=90∘

We know that angles opposite to equal sides are also equal.

Therefore, ∠B = ∠C

Also, the sum of the interior angles of a triangle is 180∘ .

So, we have :

∠A + ∠B + ∠C = 180∘

or 90∘+ 2∠B = 180∘

or ∠B = 45∘

As, ∠B = ∠C

So, angleC =\ 45^{\circ}$

Q8 Show that the angles of an equilateral triangle are 60∘ each.

Answer:

Consider a triangle ABC which has all sides equal as shown in the figure.

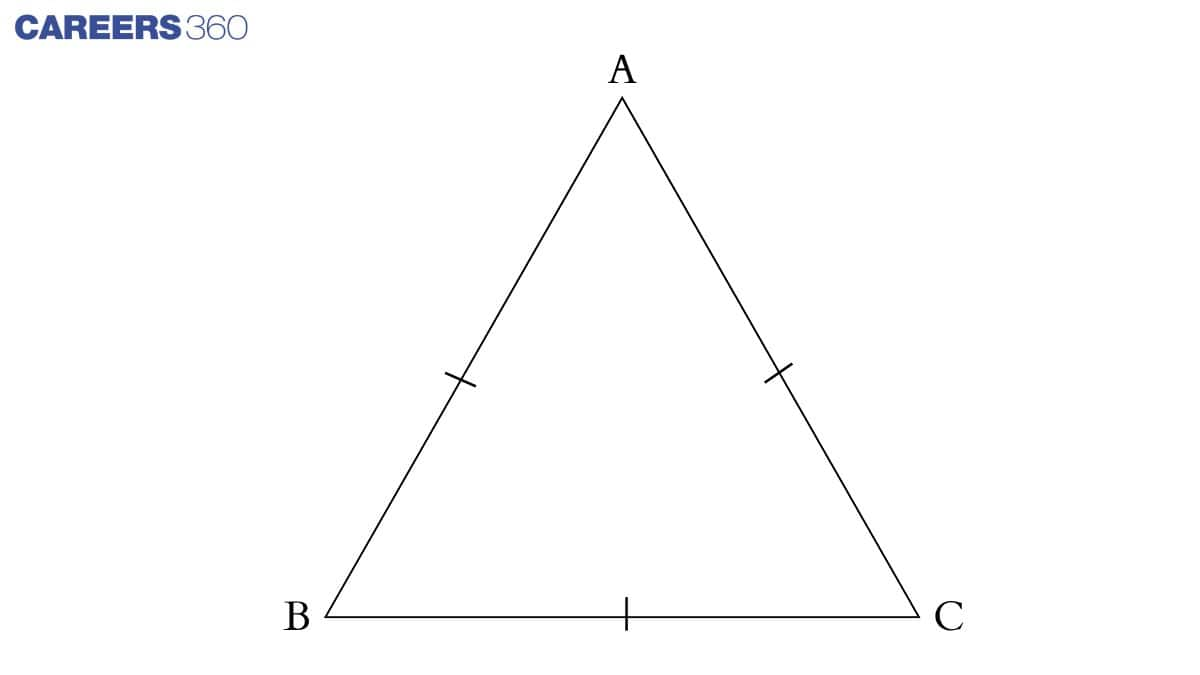
We know that angles opposite to equal sides are equal.

Therefore: ∠A = ∠B = ∠C

Also, the sum of the interior angles of a triangle is 180∘ .

Hence, ∠A + ∠B + ∠C = 180∘

or 3∠A = 180∘

or ∠A = 60∘

As, all the angles of the equilateral triangle are equal, thus ∠A = ∠B = ∠C = 60∘.