NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3 - Triangles

Q1 (i) ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig.). If AD is extended to intersect BC at P, show that ΔABD≅ΔACD

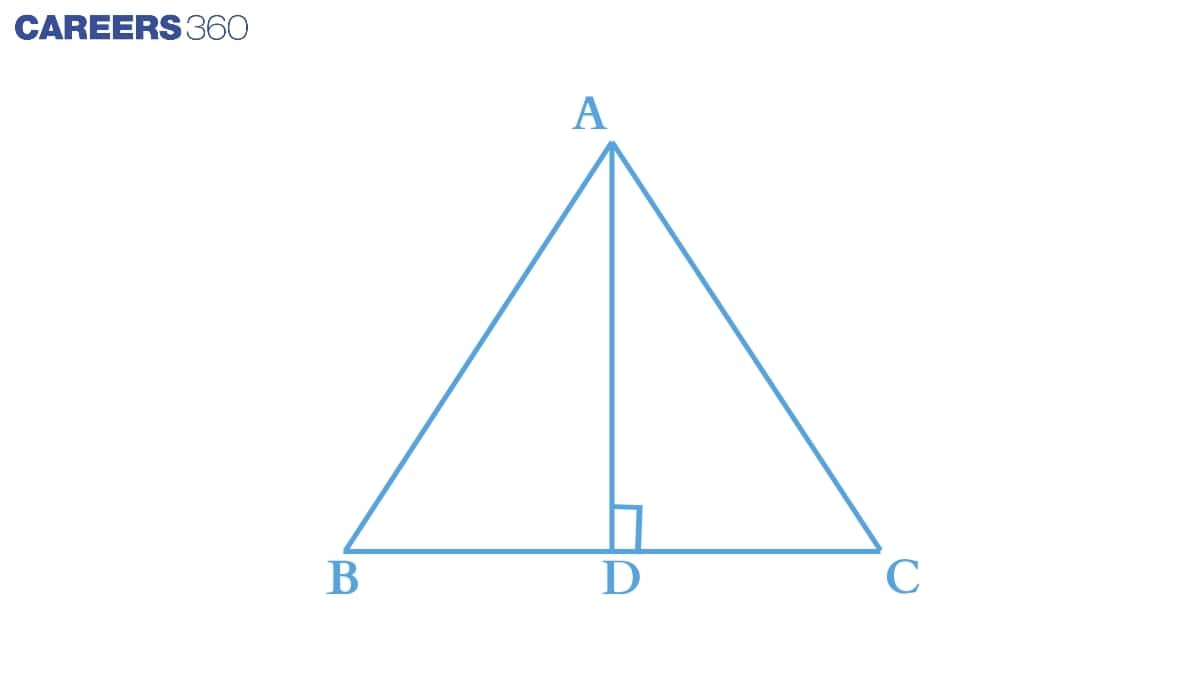
Answer:

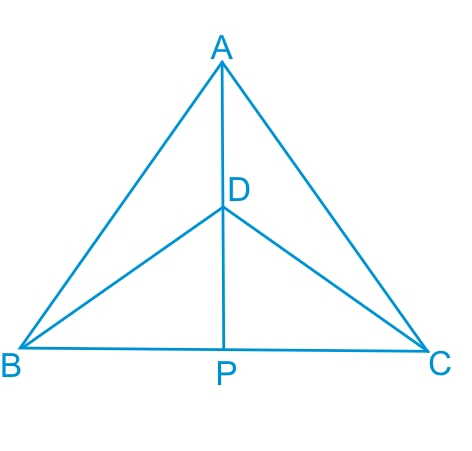
Consider ΔABD and ΔACD ,

(i) AD = AD (Common)

(ii) AB = AC (Isosceles triangle)

(iii) BD = CD (Isosceles triangle)

Thus by SSS congruency we can conclude that :

ΔABD≅ΔACD

Q1 (ii) Triangles ABC and Triangle DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig). If AD is extended to intersect BC at P, show that ΔABP≅ΔACP

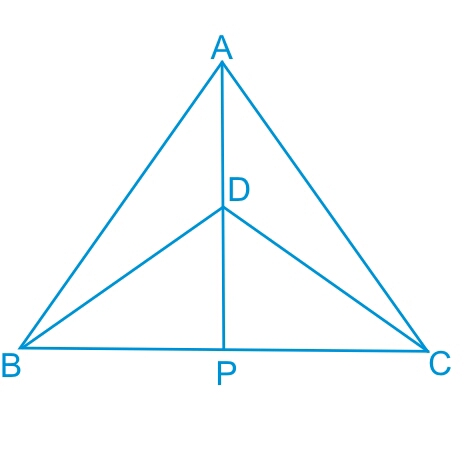
Answer:

Consider ΔABP and ΔACP ,

(i) AP is common side in both the triangles.

(ii) ∠PAB = ∠PAC (This is obtained from the c.p.c.t. as proved in the previous part.)

(iii) AB = AC (Isosceles triangles)

Thus by SAS axiom, we can conclude that :

ΔABP≅ΔACP

Q1 (iii) ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig.). If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D .

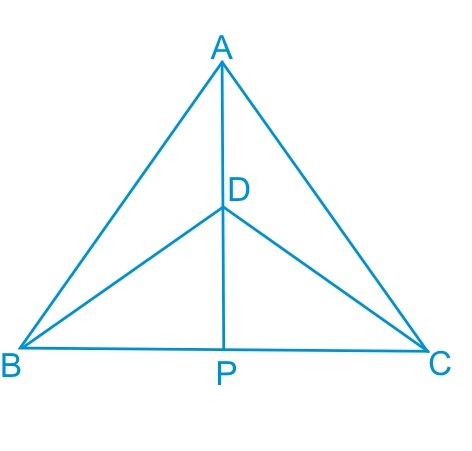
Answer:

In the first part, we have proved that ΔABD≅ΔACD .

So, by c.p.c.t. ∠PAB = ∠PAC .

Hence AP bisects ∠A .

Now consider ΔBPD and ΔCPD ,

(i) PD = PD (Common)

(ii) BD = CD (Isosceles triangle)

(iii) BP = CP (by c.p.c.t. from the part (b))

Thus by SSS congruency we have :

ΔBPD ≅ ΔCPD

Hence by c.p.c.t. we have : ∠BDP = ∠CDP

or AP bisects ∠D .

Q1 (iv) ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig.). If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.

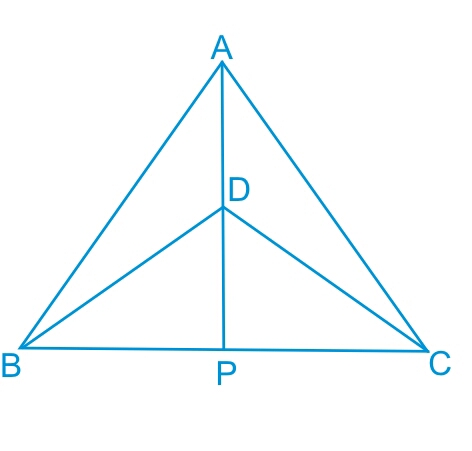
Answer:

In the previous part we have proved that ΔBPD ≅ ΔCPD .

Thus by c.p.c.t. we can say that : ∠BPD = ∠CPD

Also, BP = CP

SInce BC is a straight line, thus : ∠BPD + ∠CPD = 180∘

or 2∠BPD = 180∘

or ∠BPD = 90∘

Hence it is clear that AP is a perpendicular bisector of line BC.

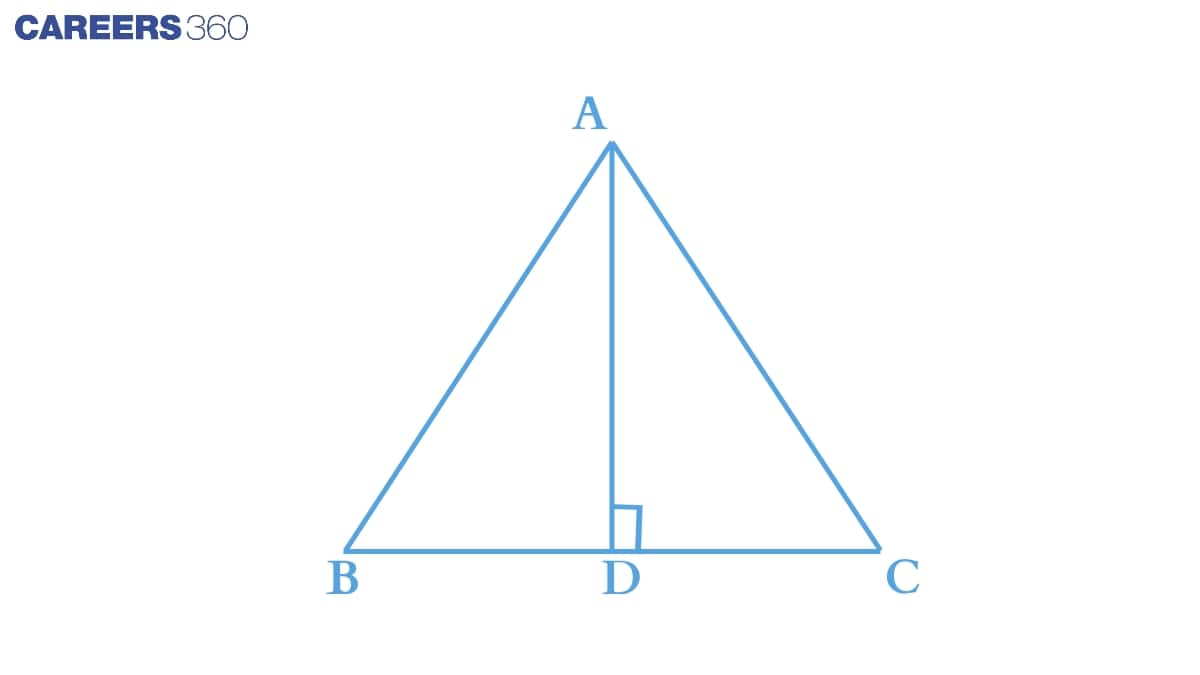
Q2 (i) AD is an altitude of an isosceles triangle ABC in which AB=AC . Show that AD bisects BC

Answer:

Consider ΔABD and ΔACD ,

(i) AB = AC (Given)

(ii) AD = AD (Common in both triangles)

(iii) ∠ADB = ∠ADC = 90∘

Thus by RHS axiom we can conclude that :

ΔABD ≅ ΔACD

Hence by c.p.c.t. we can say that : BD = CD or AD bisects BC.

Q2 (ii) AD is an altitude of an isosceles triangle ABC in which AB=AC . Show that AD bisects ∠A .

Answer:

In the previous part of the question we have proved that ΔABD ≅ ΔACD

Thus by c.p.c.t., we can write :

∠BAD = ∠CAD

Hence AD bisects ∠A .

Q3 Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig). Show that:

(i) ΔABM≅ΔPQN

(ii) ΔABC≅ΔPQR

Answer:

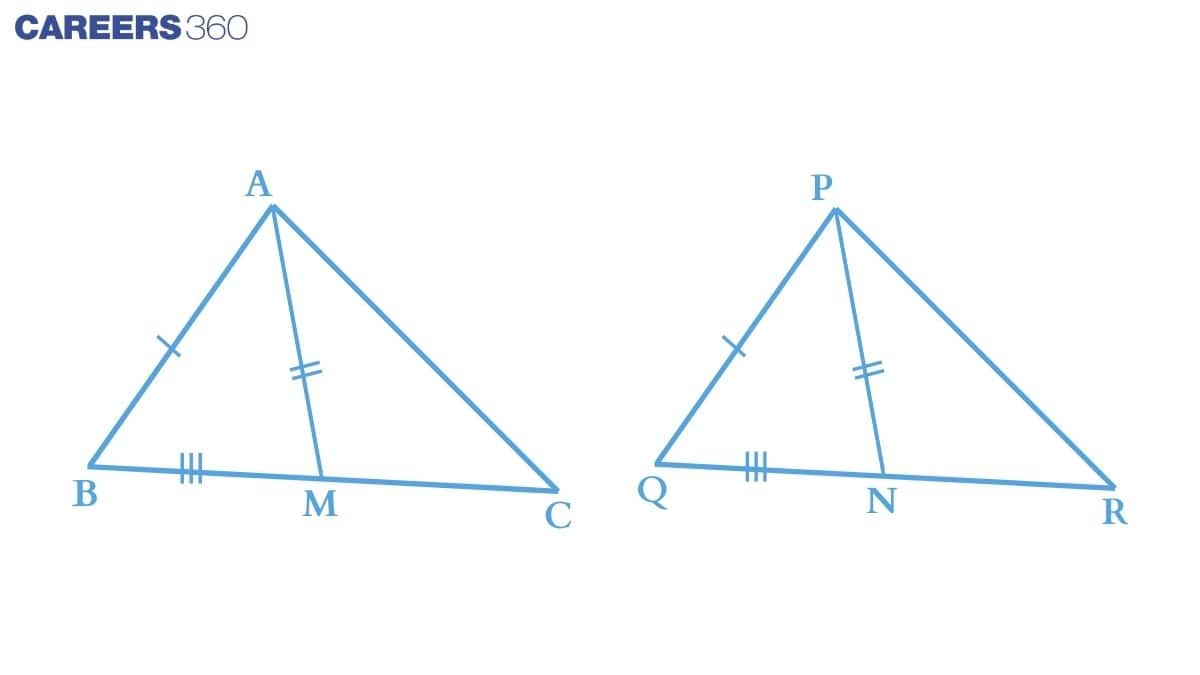
(i) From the figure we can say that :

BC = QR

or 12BC = 12QR

or BM = QN

Now, consider ΔABM and ΔPQN ,

(a) AM = PN (Given)

(b) AB = PQ (Given)

(c) BM = QN (Prove above)

Thus by SSS congruence rule, we can conclude that :

ΔABM≅ΔPQN

(ii) Consider ΔABC and ΔPQR :

(a) AB = PQ (Given)

(b) ∠ABC = ∠PQR (by c.p.c.t. from the above proof)

(c) BC = QR (Given)

Thus by SAS congruence rule,

ΔABC≅ΔPQR

Q4 BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Answer:

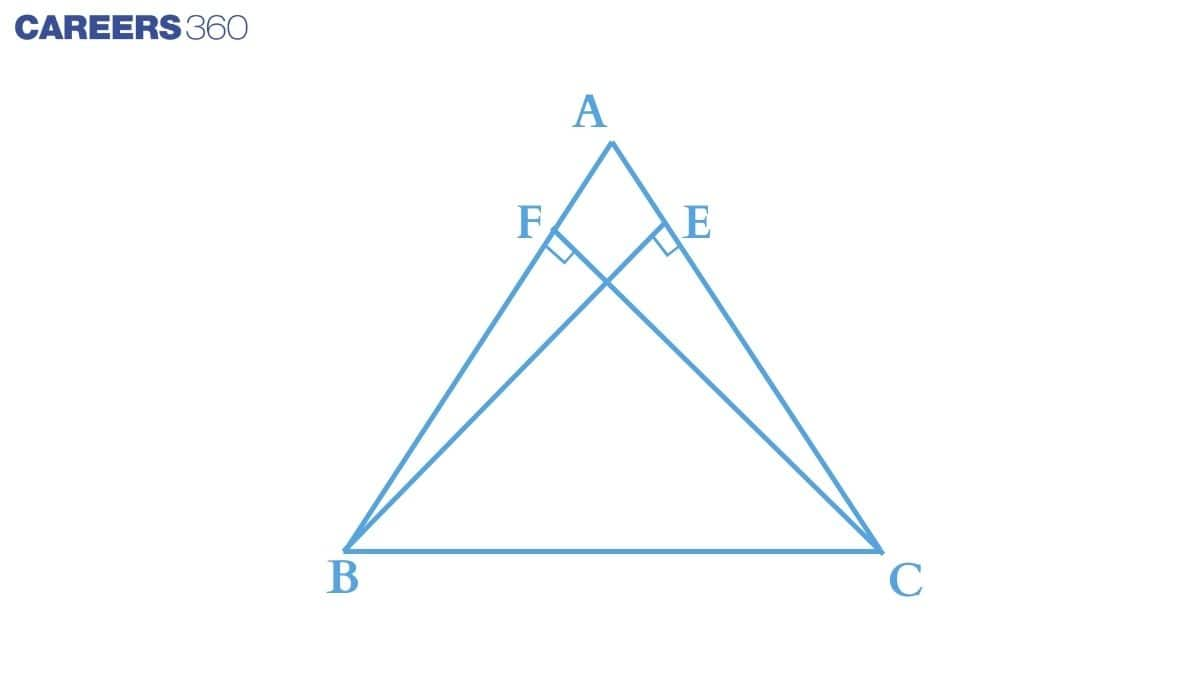
Using the given conditions, consider ΔBEC and ΔCFB ,

(i) ∠BEC = ∠CFB (Right angle)

(ii) BC = BC (Common in both the triangles)

(iii) BE = CF (Given that altitudes are of the same length. )

Thus by RHS axiom, we can say that : ΔBEC ≅ΔCFB

Hence by c.p.c.t., ∠B = ∠C

And thus AB = AC (sides opposite to equal angles are also equal). Thus ABC is an isosceles triangle.

Q5 ABC is an isosceles triangle with AB=AC . Draw AP⊥BC to show that ∠B=∠C .

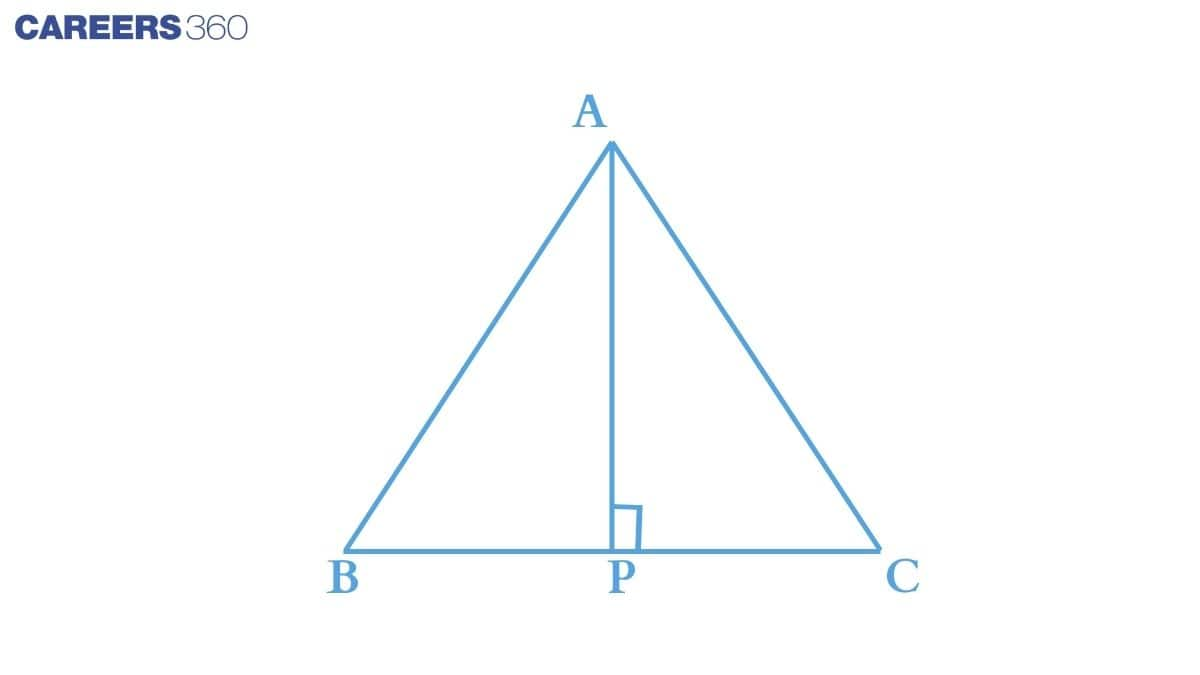
Answer:

Consider ΔABP and ΔACP ,

(i) ∠APB = ∠APC = 90∘ (Since it is given that AP is altitude.)

(ii) AB = AC (Isosceles triangle)

(iii) AP = AP (Common in both triangles)

Thus by RHS axiom we can conclude that :

ΔABP ≅ΔACP

Now, by c.p.c.t.we can say that :

∠B = ∠C