NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1 - Triangles

Q1 In quadrilateral $\small ABCD$ , $\small AC=AD$ and $\small AB$ bisects $\small \angle A$ (see Fig.7.16). Show that $\small \Delta ABC\cong \Delta ABD$ . What can you say about $\small BC$ and $\small BD$ ?

Solution:
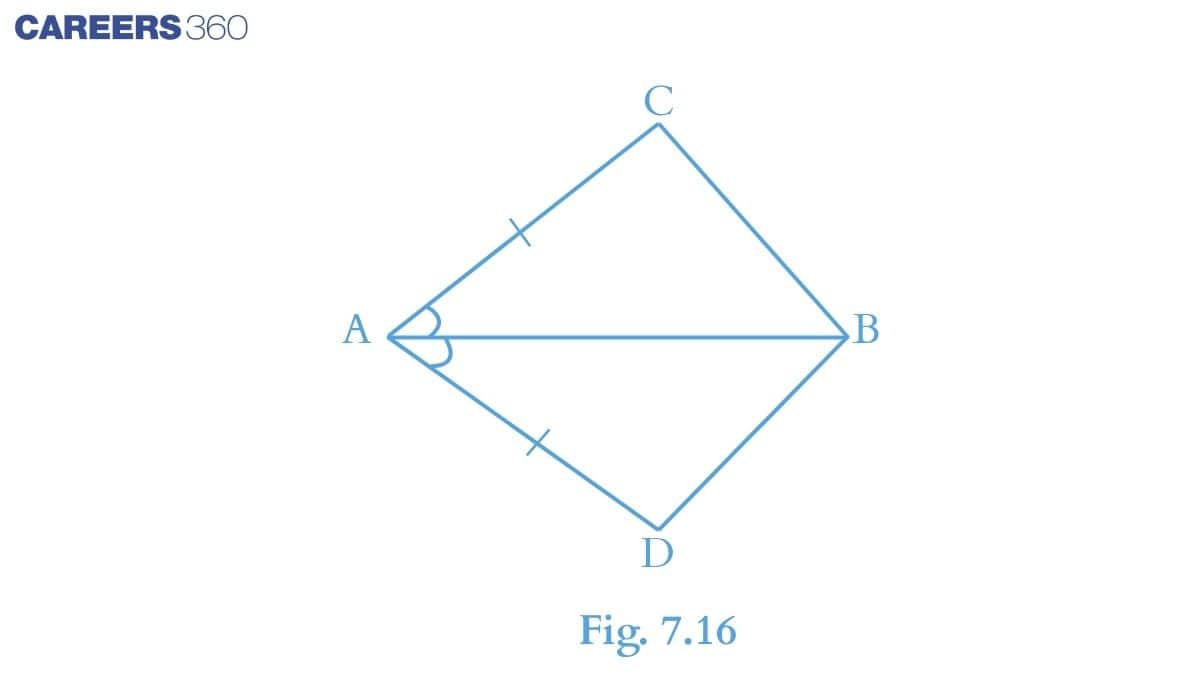
In the given triangles, we are given that:-
In $\small \Delta ABC$ and $\small \Delta ABD$
(i) $\small AC=AD$
(ii) Further, it is given that AB bisects angle A.
Thus, $\angle$ BAC $=\ \angle$ BAD.
(iii) Side AB is common to both triangles. $AB=AB$
Hence by SAS congruence, we can say that: $\small \Delta ABC\cong \Delta ABD$
By C.P.C.T. (corresponding parts of congruent triangles are equal) we can say that $BC\ =\ BD$

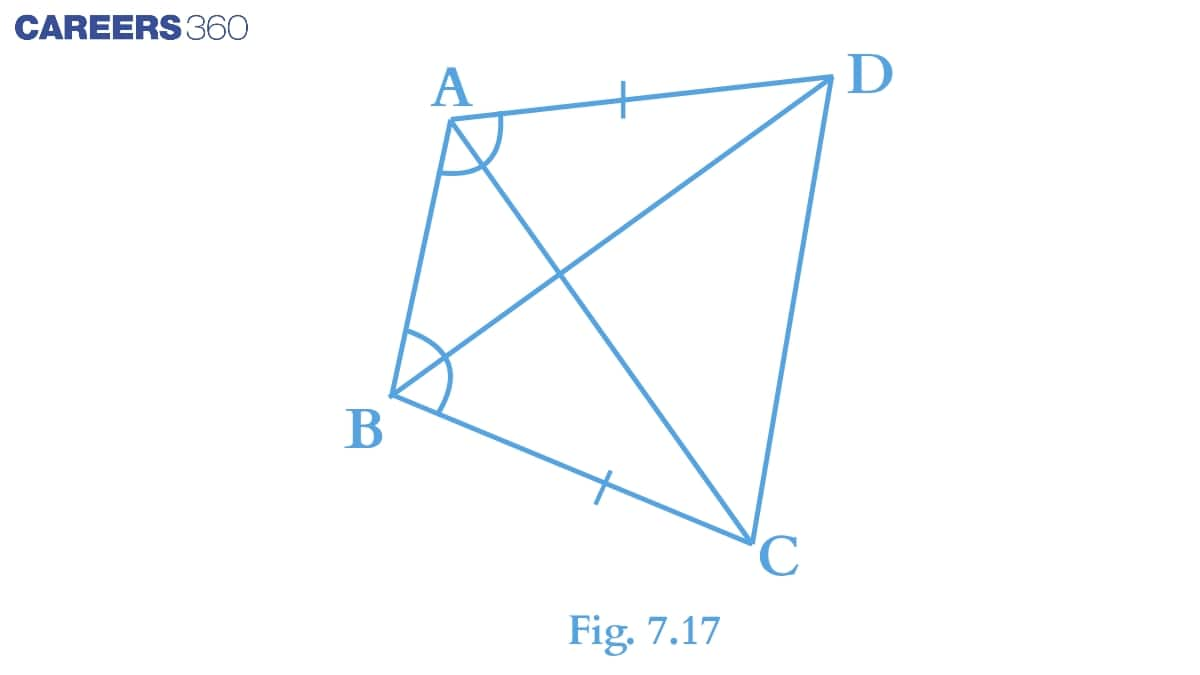
Q2 (i) $ABCD$ is a quadrilateral in which $\small AD=BC$ and $\small \angle DAB= \angle CBA$ (see Fig. 7.17). Prove that $\small \Delta ABD\cong \Delta BAC$ .

Solution:
In $\small \Delta ABD$ and $\Delta BAC$
(i) AD = BC
(ii) $\small \angle DAB= \angle CBA$
(iii) AB = AB (Side AB is common to both the triangles)
So, by SAS congruence, we can write :
$\small \Delta ABD\cong \Delta BAC$

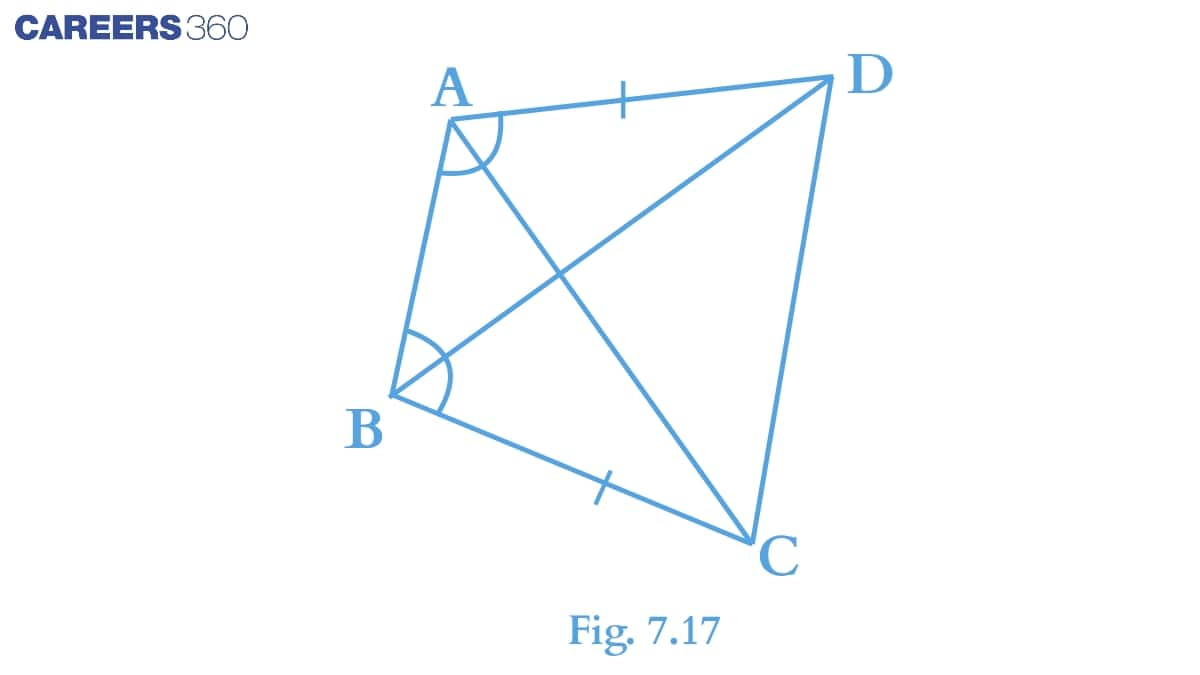
Q2 (ii) ABC $\small ABCD$ is a quadrilateral in which $\small AD=BC$ and $\small \angle DAB=\angle CBA$ (see Fig.7.17). Prove that $\small BD=AC$

Solution:
In the previous part, we have proved that $\small \Delta ABD\cong \Delta BAC$.
Thus, by C.P.C.T., we can write: $\small BD=AC$

Q2 (iii) $\small ABCD$ is a quadrilateral in which $\small AD=BC$ and $\small \angle DAB= \angle BAC$ (see Fig.7.17). Prove that $\small \angle ABD= \angle BAC$ .

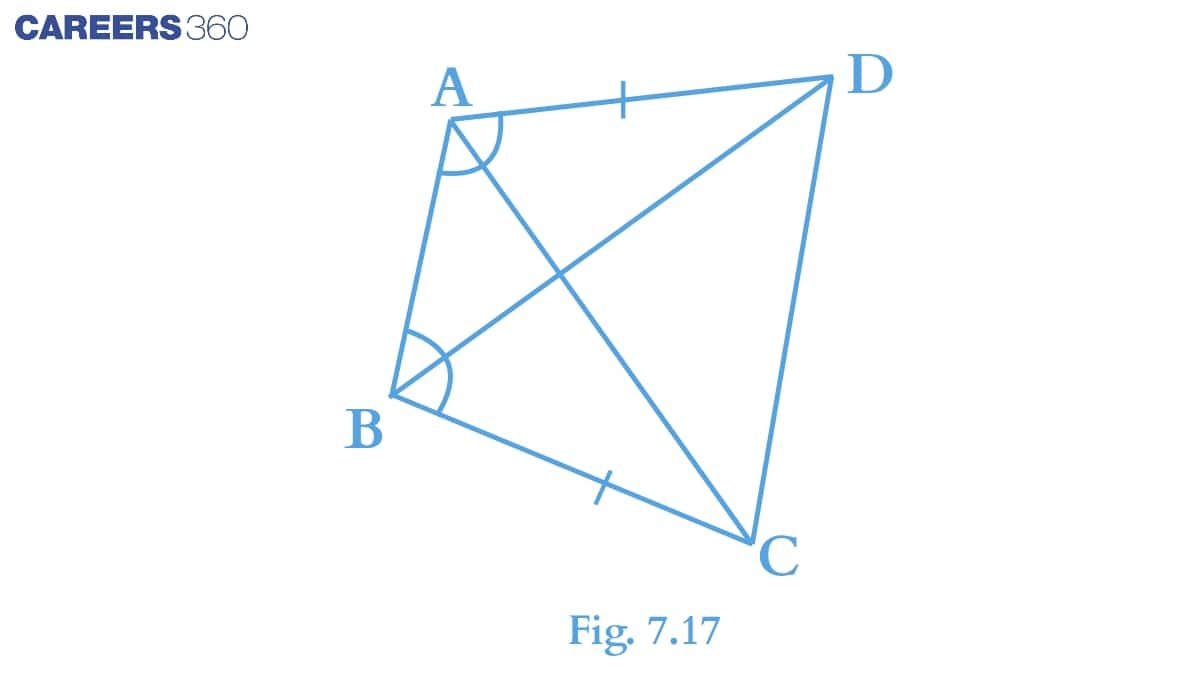
Solution:
In the first part we have proved that $\small \Delta ABD\cong \Delta BAC$.
Thus, by C.P.C.T., we can conclude,
$\small \angle ABD= \angle BAC$ ∠ABD=∠B

Q3. $\small AD$ and $\small BC$ are equal perpendiculars to a line segment $\small AB$ (see Fig.). Show that $\small CD$ bisects $\small AB$ .

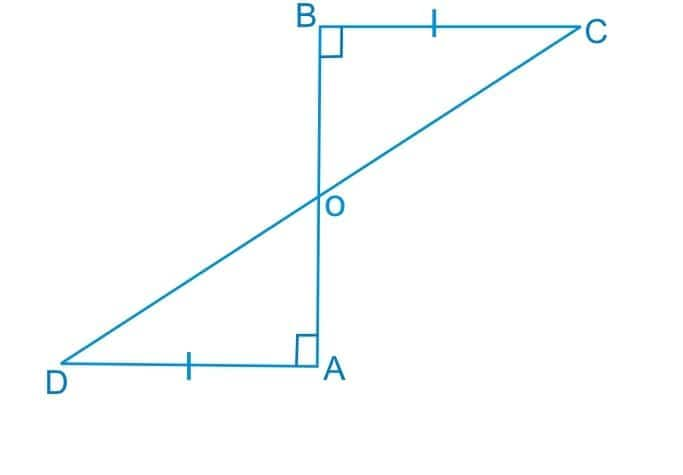
Solution:
In the given figure consider $\Delta$ AOD and $\Delta$ BOC.
(i) AD = BC (Given)
(ii) $\angle$ A = $\angle$ B (Given that the line AB is perpendicular to AD and BC)
(iii) $\angle$ AOD = $\angle$ BOC (Vertically opposite angles).
Thus by AAS Postulate, we have
$\Delta AOD\ \cong \ \Delta BOC$
Hence, by C.P.C.T. we can write: $AO\ =\ OB$
Thus, CD bisects AB.

Q4. $\small l$ and $\small m$ are two parallel lines intersected by another pair of parallel lines $\small p$ and $\small q$ (see Fig.7.19 ). Show that $\small \Delta ABC\cong \Delta CDA$ .

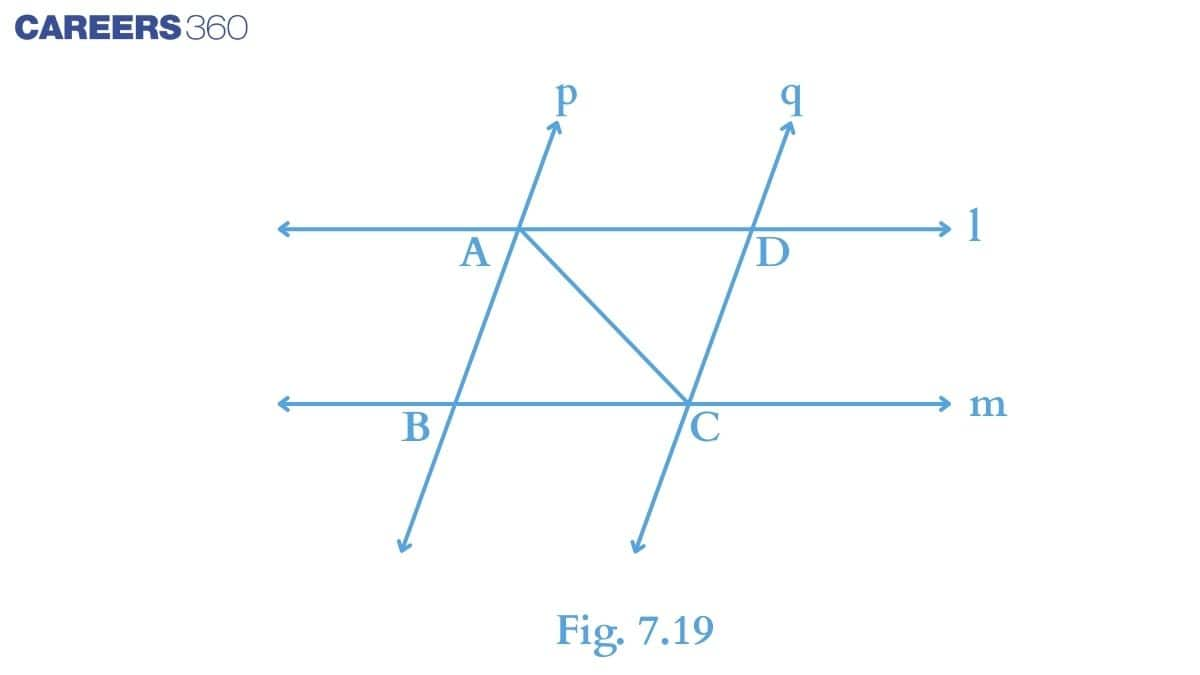
Solution:
In the given figure, consider $\Delta$ ABC and $\Delta$ CDA :
(i) $\angle\ BCA\ =\ \angle DAC$ (Alternate interior angles)
(ii) $\angle\ BAC\ =\ \angle DCA$ (Alternate interior angles)
(iii) Side AC is common in both the triangles.
Thus by ASA congruence, we have:
$\Delta ABC\ \cong \ \Delta CDA$

ΔABC ≅ ΔCD

Q5 (i) Line $\small l$ is the bisector of an angle $\small \angle A$ and B is any point on $\small l$ . $\small BP$ and $\small BQ$ are perpendiculars from $\small B$ to the arms of $\small \angle A$ (see Fig. 7.20). Show that: $\small \Delta APB\cong \Delta AQB$

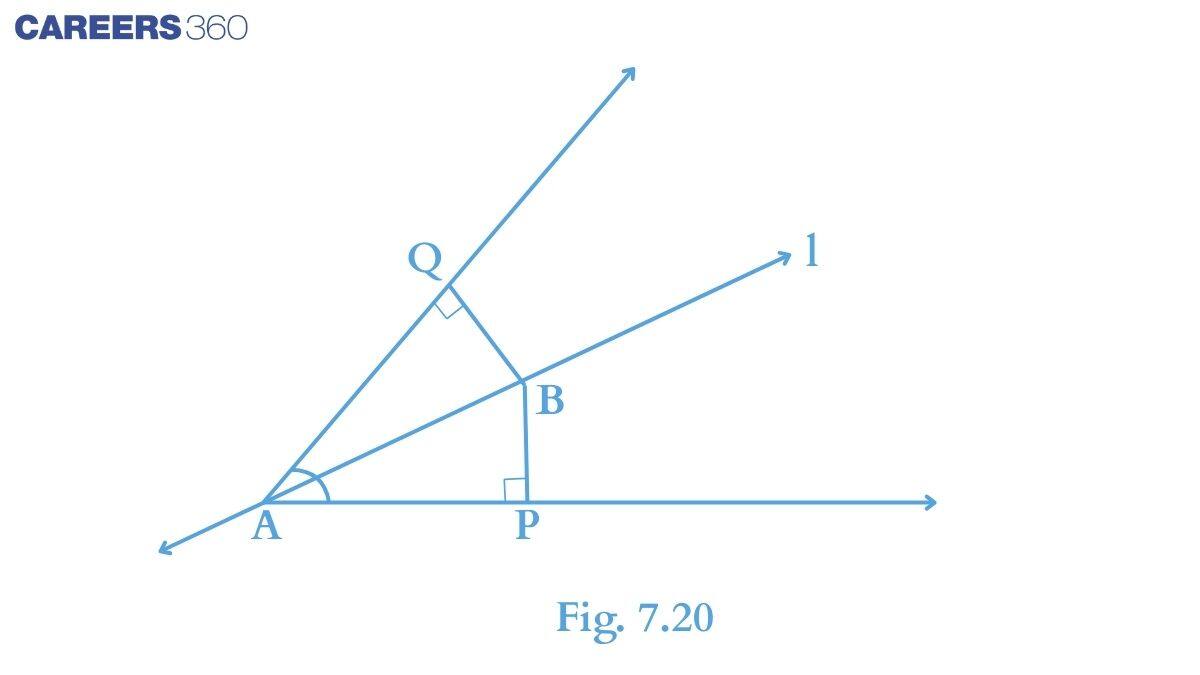
Solution:
In the given figure consider $\small \Delta APB$ and $\small \Delta AQB$,
(i) $\angle P\ =\ \angle Q$ (Right angle)
(ii) $\angle BAP\ =\ \angle BAQ$ (Since it is given that I is bisector)
(iii) Side AB is common to both triangles.
Thus, AAS congruence, we can write:
$\small \Delta APB\cong \Delta AQB$

ΔAPB≅ΔAQ

Q5 (ii) Line $\small l$ is the bisector of an angle $\small \angle A$ and $\small B$ is any point on $\small l$ . $\small BP$ and $\small BQ$ are perpendiculars from $\small B$ to the arms of $\small \angle A$ (see Fig. 7.20). Show that: $\small BP=BQ$ or $\small B$ is equidistant from the arms of $\small \angle A$ .

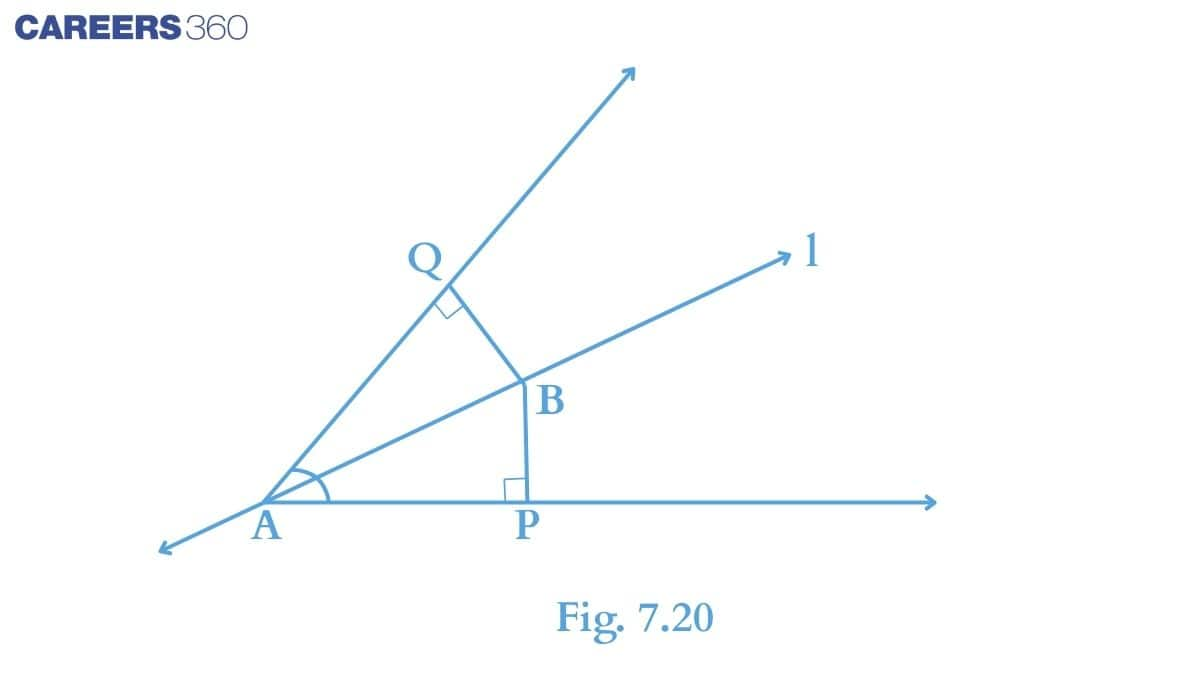
Solution:
In the previous part, we have proved that $\small \Delta APB\cong \Delta AQB$.
Thus, by C.P.C.T., we can write:
$BP\ =\ BQ$
Thus, B is equidistant from the arms of angle A.

Q6. In Fig, $\small AC=AE,AB=AD$ and $\small \angle BAD= \angle EAC$ . Show that $\small BC=DE$ .

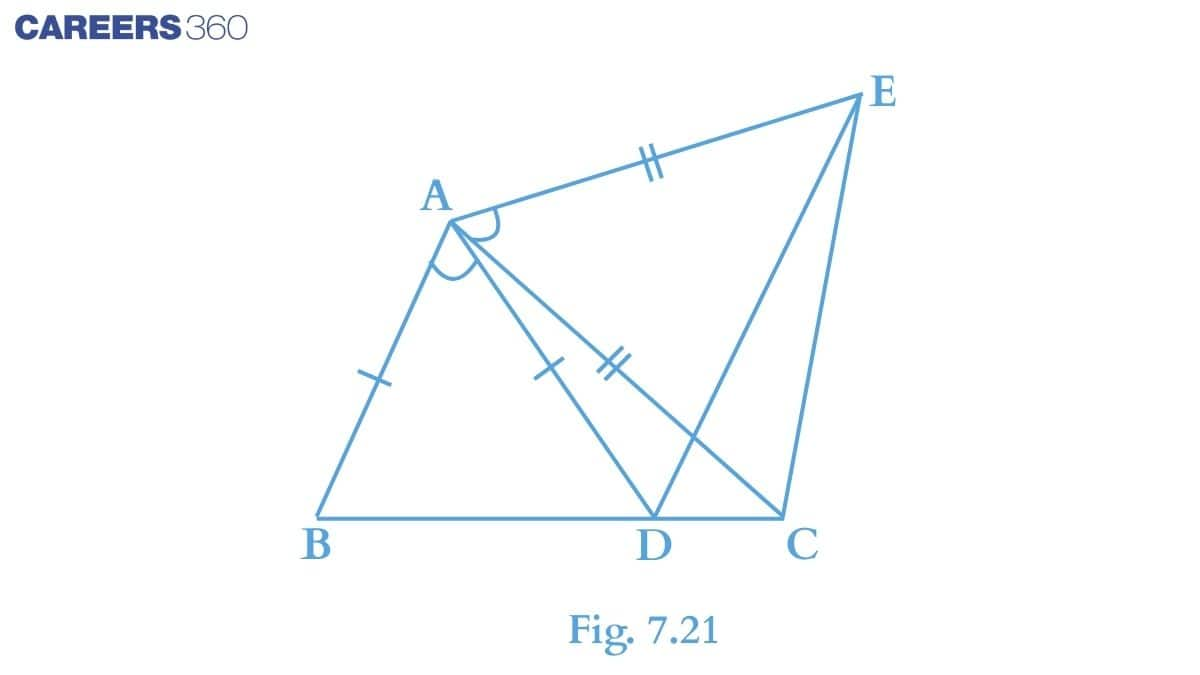
Solution:
From the given figure following result can be drawn:-
$\angle BAD\ =\ \angle EAC$
Adding $\angle DAC$ to both sides, we get:
$\angle BAD\ +\ \angle DAC\ =\ \angle EAC\ +\ \angle DAC$
$\angle BAC\ =\ \angle EAD$
Now consider $\Delta ABC$ and $\Delta ADE$ , :-
(i) $AC\ =\ AE$ (Given)
(ii) $\angle BAC\ =\ \angle EAD$ (Proved above)
(iii) $AB\ =\ AD$ (Given)
Thus, by SAS congruence, we can say that :
$\Delta ABC\ \cong \ \Delta ADE$
Hence by C.P.C.T., we can say that : $BC\ =\ DE$

Q7 (i) $\small AB$ is a line segment and $\small P$ is its mid-point. $\small D$ and $\small E$ are points on the same side of $\small AB$ such that $\small \angle BAD=\angle ABE$ and $\small \angle EPA=\angle DPB$ (see Fig). Show that $\small \Delta DAP\cong \Delta EBP$

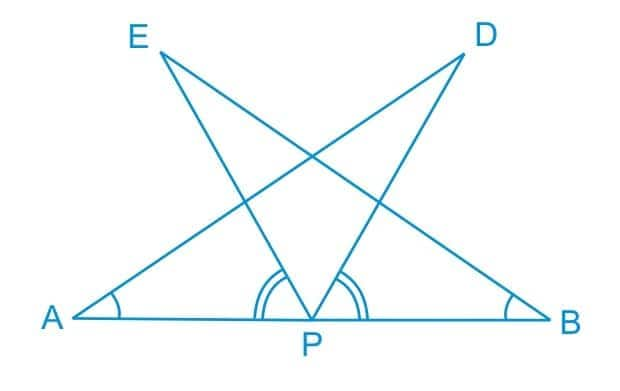
Solution:
From the figure, it is clear that :
$\angle EPA\ =\ \angle DPB$
Adding $\angle DPE$ both sides, we get:
$\angle EPA\ +\ \angle DPE =\ \angle DPB\ +\ \angle DPE$
Or $\angle DPA =\ \angle EPB$
Now, consider $\Delta DAP$ and $\Delta EBP$ :
(i) $\angle DPA =\ \angle EPB$ (Proved above)
(ii) $AP\ =\ BP$ (Since P is the midpoint of line AB)
(iii) $\small \angle BAD=\angle ABE$ (Given)
Hence, by ASA congruence, we can say that:
$\small \Delta DAP\cong \Delta EBP$

Q7 (ii) AB is a line segment and P is its midpoint. D and E are points on the same side of AB such that $\small \angle BAD=\angle ABE$ and $\small \angle EPA=\angle DPA$ (see Fig). Show that $\small AD=BE$

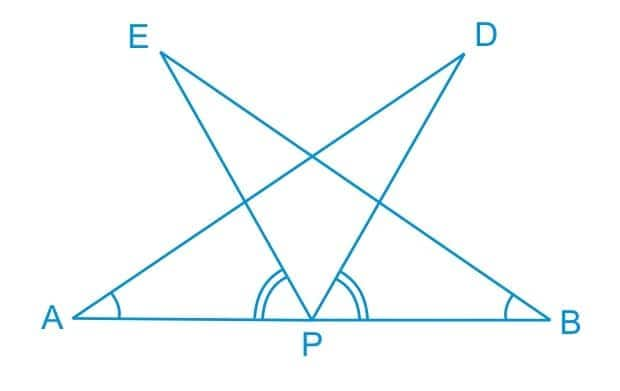
Solution:
In the previous part we have proved that $\small \Delta DAP\cong \Delta EBP$.
Thus, by C.P.C.T., we can say that:
$\small AD=BE$

Q8 (i) In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that $\small DM=CM$ . Point D is joined to point B (see Fig.7.23). Show that: $\small \Delta AMC\cong \Delta BMD$

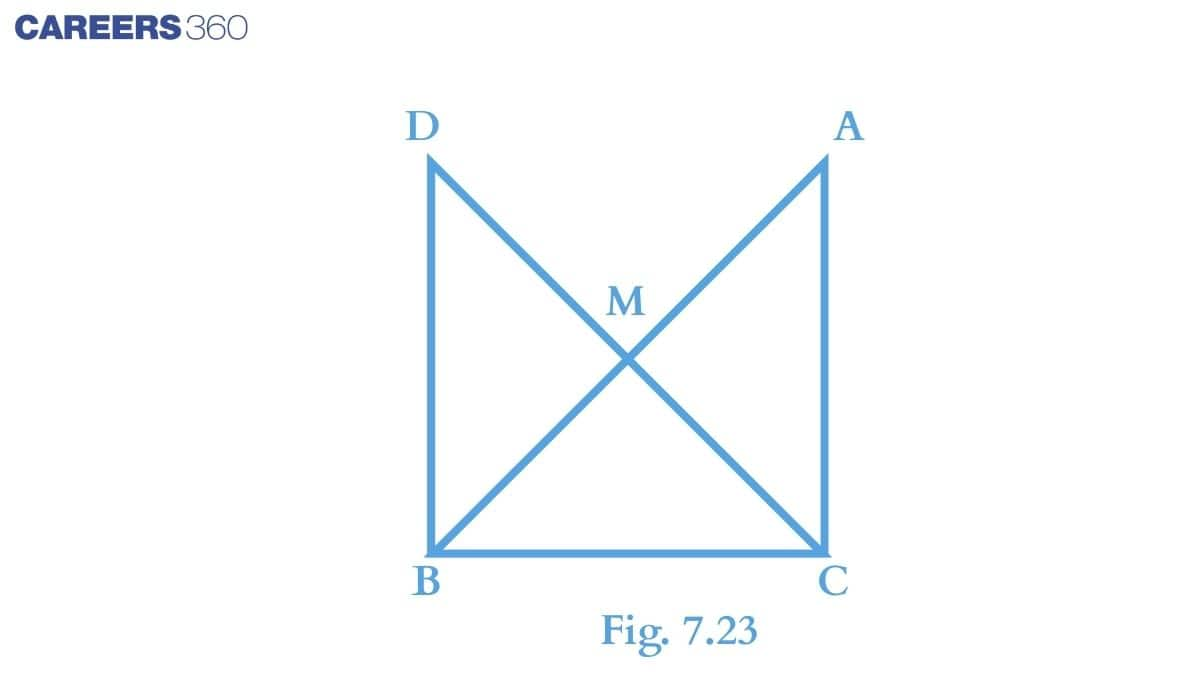
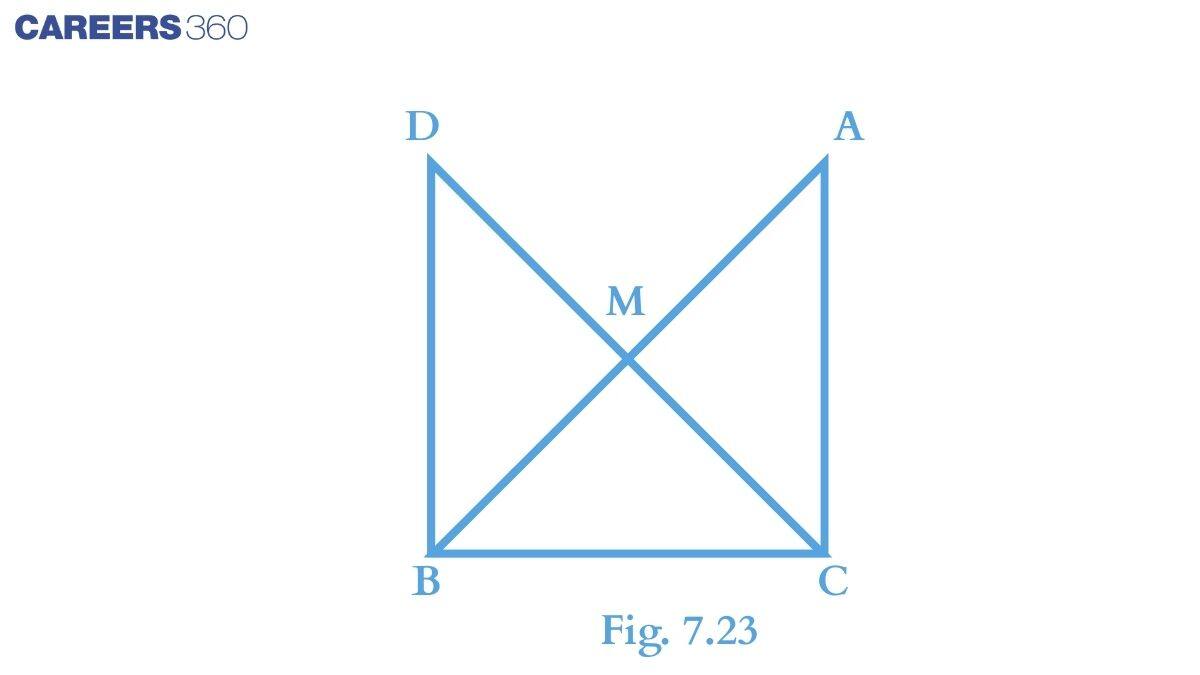
Solution:Consider $\Delta AMC$ and $\Delta BMD$,
(i) $AM\ =\ BM$ (Since M is the mid-point)
(ii) $\angle CMA\ =\ \angle DMB$ (Vertically opposite angles are equal)
(iii) $CM\ =\ DM$ (Given)
Thus, by SAS congruency, we can conclude that:
$\small \Delta AMC\cong \Delta BMD$

Q8 (ii) In right triangle ABC, right angled at C, M is the midpoint of the hypotenuse AB. C is joined to M and produced to a point D such that $\small DM=CM$ . Point D is joined to point B (see Fig.7.23). Show that: $\small \angle DBC$ is a right angle.

Solution:
In the previous part, we have proved that $\small \Delta AMC\cong \Delta BMD$.
By c.p.c.t. we can say that: $\angle ACM\ =\ \angle BDM$
This implies side AC is parallel to BD.
Thus, we can write : $\angle ACB\ +\ \angle DBC\ =\ 180^{\circ}$ (Co-interior angles)
And, $90^{\circ}\ +\ \angle DBC\ =\ 180^{\circ}$
Or $\angle DBC\ =\ 90^{\circ}$
Hence, $\small \angle DBC$ is a right angle.

Q8 (iii) In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that $\small DM=CM$ . Point D is joined to point B (see Fig.7.23). Show that: $\small \Delta DBC\cong \Delta ACB$

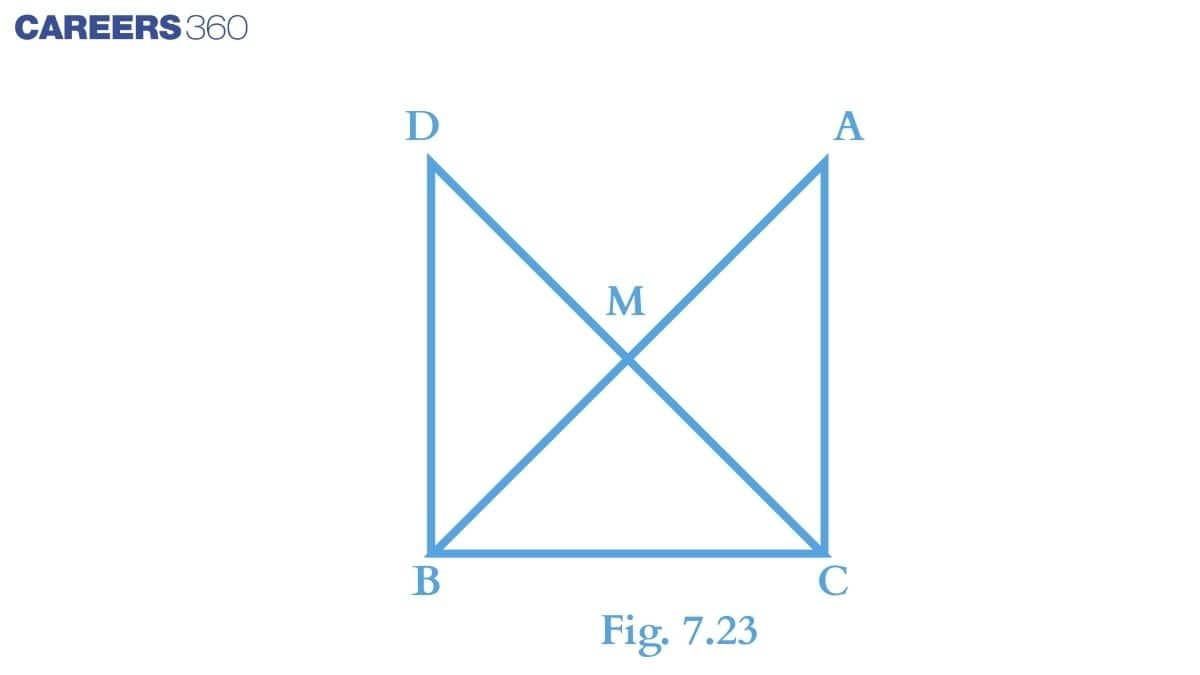
Solution:Consider $\Delta DBC$ and $\Delta ACB$,
(i) $BC\ =\ BC$ (Common in both the triangles)
(ii) $\angle ACB\ =\ \angle DBC$ (Right angle)
(iii) $DB\ =\ AC$ (By c.p.c.t. from part (a) of the question.)
Thus, SAS congruence we can conclude that:
$\small \Delta DBC\cong \Delta ACB$

Q8 (iv) In right triangle ABC, right angled at C, M is the midpoint of hypotenuse AB. C is joined to M and produced to a point D such that $\small DM=CM$ . Point D is joined to point B (see Fig.7.23). Show that: $\small CM=\frac{1}{2}AB$

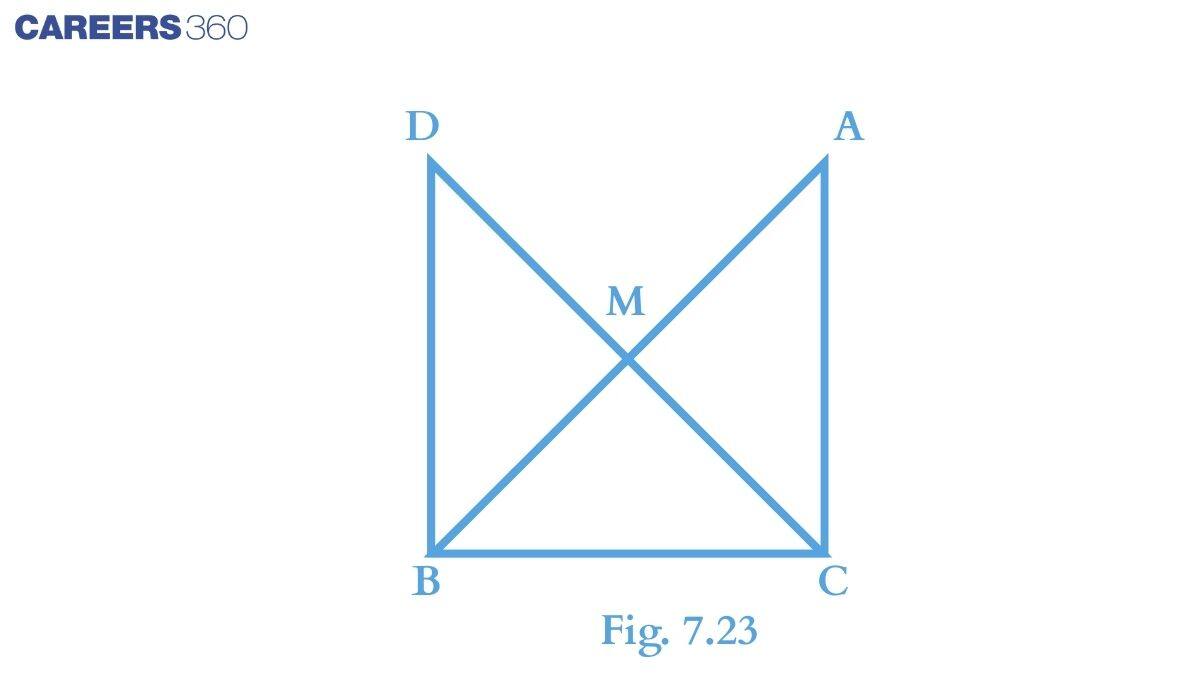
Solution:

In the previous part, we have proved that

$\Delta DBC\ \cong \ \Delta ACB$.

Thus by c.p.c.t., we can write : $DC\ =\ AB$

$DM\ +\ CM\ =\ AM\ +\ BM$

Or $CM\ +\ CM\ =\ AB$ (Since M is the midpoint.)

Or $\small CM=\frac{1}{2}AB$.

Hence proved.