Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 7.4 Class 9 Maths Chapter 7 - Triangles

NCERT Solutions for Exercise 7.4 Class 9 Maths Chapter 7 - Triangles

Edited By Safeer PP | Updated on Jul 18, 2022 02:34 PM IST

Exercise 7.4 Class 9 Maths deals with problems related to the relationship between the triangle's unequal sides and the angles on the opposite side. When two triangle sides are unequal, the angle opposite to the bigger side(longest side) is larger.

Triangle disparity: The sum of the lengths of any two triangle sides should be always greater than the length of the third side. In any triangle, the side opposite to the bigger angle is longer. Exercise 7.4 Class 9 Maths incorporates the outline of all activities and their application. Thus, we need to go through the outline of the part. At the point when two figures have the same (and exact) shape and size, they are supposed to be congruent.

This Story also Contains
  1. Triangles Class 9 Chapter 7 Exercise: 7.4
  2. More About NCERT Solutions for Class 9 Maths Exercise 7.4 -
  3. Benefits of NCERT Solutions for Class 9 Maths Exercise 7.4
  4. NCERT Solutions of Class 10 Subject Wise
  5. Subject Wise NCERT Exemplar Solutions

Along with NCERT book Class 9 Maths, chapter 8 exercise 7.4 the following exercises are also present.

Triangles Class 9 Chapter 7 Exercise: 7.4

Q1 Show that in a right-angled triangle, the hypotenuse is the longest side.

Answer:

Consider a right-angled triangle ABC with right angle at A.

We know that the sum of the interior angles of a triangle is 180.

So, \angle A\ +\ \angle B\ +\ \angle C\ =\ 180^{\circ}

or 90^{\circ}\ +\ \angle B\ +\ \angle C\ =\ 180^{\circ}

or \angle B\ +\ \angle C\ =\ 90^{\circ}

Hence \angle B and \angle C are less than \angle A ( 90^{\circ} ).

Also, the side opposite to the largest angle is also the largest.

Hence the side BC is largest is the hypotenuse of the \Delta ABC .

Hence it is proved that in a right-angled triangle, the hypotenuse is the longest side.

Q2 In Fig, sides AB and AC of \small \Delta ABC are extended to points P and Q respectively. Also, \small \angle PBC < \angle QCB . Show that \small AC> AB .

1640157763824

Answer:

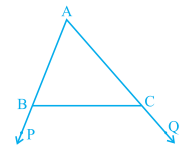
We are given that,

\small \angle PBC < \angle QCB ......................(i)

Also, \angle ABC\ +\ \angle PBC\ =\ 180^{\circ} (Linear pair of angles) .....................(ii)

and \angle ACB\ +\ \angle QCB\ =\ 180^{\circ} (Linear pair of angles) .....................(iii)

From (i), (ii) and (iii) we can say that :

\angle ABC\ > \ \angle ACB

Thus AC\ > AB ( Sides opposite to the larger angle is larger.)

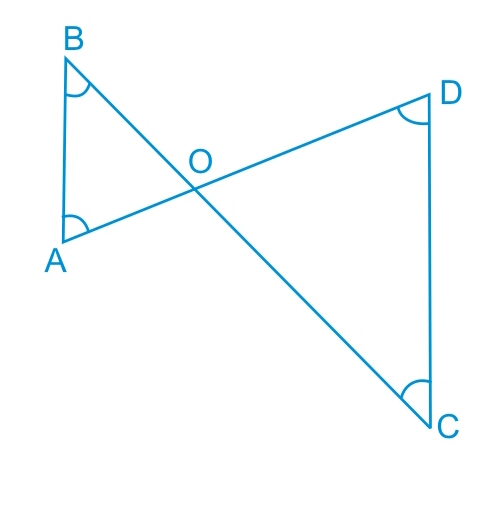
Q3 In Fig., \small \angle B <\angle A and \small \angle C <\angle D . Show that \small AD <BC .

1640157791848

Answer:

In this question, we will use the property that sides opposite to larger angle are larger.

We are given \small \angle B <\angle A and \small \angle C <\angle D .

Thus, BO\ > AO ..............(i)

and OC\ > OD ...............(ii)

Adding (i) and (ii), we get :

AO\ +\ OD\ <\ BO\ +\ OC

or AD\ <\ BC

Hence proved.

Q4 AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig.). Show that \small \angle A>\angle C and \small \angle B>\angle D .

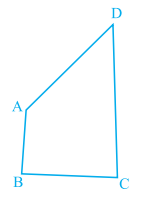
1640157840642

Answer:

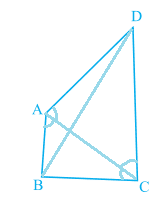
1640157864575

Consider \Delta ADC in the above figure :

AD\ <\ CD (Given)

Thus \angle CAD\ > \angle ACD (as angle opposite to smaller side is smaller)

Now consider \Delta ABC ,

We have : BC\ > AB

and \angle BAC\ > \angle ACB

Adding the above result we get,

\angle BAC\ +\ \angle CAD > \angle ACB\ +\ \angle ACD

or \small \angle A>\angle C

Similarly, consider \Delta ABD ,

we have AB\ <\ AD

Therefore \angle ABD\ > \angle ADB

and in \Delta BDC we have,

CD\ >\ BC

and \angle CBD\ >\ \angle CDB

from the above result we have,

\angle ABD\ +\ \angle CBD\ >\ \angle ADB\ +\ \angle CDB

or \small \angle B>\angle D

Hence proved.

Q5 In Fig , \small PR>PQ and PS bisects \small \angle QPR . Prove that \small \angle PSR>\angle PSQ .

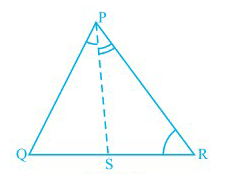
1640165632055

Answer:

We are given that \small PR>PQ .

Thus \angle PQR\ =\ \angle PRQ

Also, PS bisects \small \angle QPR , thus :

\angle QPS\ =\ \angle RPS

Now, consider \Delta QPS ,

\angle PSR\ =\ \angle PQR\ +\ \angle QPS (Exterior angle)

Now, consider \Delta PSR ,

\angle PSQ\ =\ \angle PRQ\ +\ \angle RPS

Thus from the above the result we can conclude that :

\small \angle PSR>\angle PSQ

Q6 Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Answer:

Consider a right-angled triangle ABC with right angle at B.

Then \angle B\ >\ \angle A\ or\ \angle C (Since \angle B\ =\ 90^{\circ} )

Thus the side opposite to largest angle is also largest. AC\ >\ BC\ or\ AB

Hence the given statement is proved that all line segments are drawn from a given point, not on it, the perpendicular line segment is the shortest.

More About NCERT Solutions for Class 9 Maths Exercise 7.4 -

From NCERT solutions for Class 9 Maths chapter 7 exercise 7.4, we get to know the inequalities of triangles and a few more theorems. The problems related to those are solved n the Class 9 Maths exercise 7.4. The following points also help in solving the problems of NCERT syllabus Class 9 Maths chapter 7.

  • An equilateral triangle has 60 degrees of angle on each side.
  • The two triangles are congruent if the three sides of one triangle are equal to the three sides of the other triangle (SSS Congruence Rule).
  • The two triangles are congruent if the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle (RHS Congruence Rule).

Also Read| Triangles Class 9 Notes

Benefits of NCERT Solutions for Class 9 Maths Exercise 7.4

  • Exercise 7.4 Class 9 Maths, is based on INEQUALITIES IN A TRIANGLE and its uses.

  • From Class 9 Maths chapter 7 exercise 7.4 we can roughly guess which side is greater by knowing the angle opposite to it.

  • Understanding the concepts from Class 9 Maths chapter 7 exercise 7.4 will allow us to understand the concepts related to a higher standard which includes difficult questions related to INEQUALITIES IN A TRIANGLE

Also, See

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. What is the main concept of Class 9 Maths exercise 7.4?

This exercise is about inequalities in triangles like the amount of the lengths of any two triangle sides should be more prominent than the length of the third side and so forth

2. What is a scalene triangle?

A scalene triangle is a triangle that has no equivalent sides. In this way, its angles are not equivalent to one another.

3. What are the necessary conditions for side length to be True for the formation of a triangle?

The necessary conditions for a triangle to be possible is:

  • Sum of any two sides must be greater than the third side

  • The difference of any two sides must be smaller than the third side

4. Can a triangle be possible with side length 13cm, 15cm and 30cm?

No, because the sum of two sides of length is 13cm and 15cm (which is 28cm) is smaller than the third side of length 30cm.

5. How can you determine which side is the greatest if all the angles of scalene triangles are given?

Since it is a scalene triangle all the three sides are unequal, the greatest angle will have the greatest side opposite to itself.  

6. The three angles of a triangle are 40, 60, and 80 degrees. Which of the side will be the largest?

Since it is a scalene triangle all the three sides are unequal, the greatest angle will have the greatest side opposite to itself.  

7. How can we determine the largest angel if all the side lengths are given to us?

The greatest side will have the greatest angle opposite to itself. 

8. Three sides of a triangle are of length 10cm, 14cm and 18cm which angle will be the greatest?

The greatest side will have the greatest angle opposite to itself.  

So, the angle opposite to the 18cm side will be the greatest one.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Karnataka Pre-University Certificate Examination

Exam Date:03 May,2024 - 03 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
Barmer teacher suspended for slapping class 3 student
01/05/2024, 17:07:10
Teacher arrested for `sexual exploitation' at Ujjain Ashram school
01/05/2024, 14:28:18
Delhi NCR schools get bomb threat; fire tender arrives, search underway
01/05/2024, 04:09:04
Education is greatest gift to society: Vice President Jagdeep Dhankhar
30/04/2024, 17:02:12
Jharkhand schools up to Class 8 closed till further orders due to heat wave
30/04/2024, 11:49:37
Delhi School EWS Admission 2024-25: Registration window opens at edudel.nic.in; eligibility
30/04/2024, 09:27:25
Education ministry asks NCERT to review, update textbooks on yearly basis
29/04/2024, 12:22:03
Back to top