NCERT Solutions for Class 8 Maths Chapter 6 help students understand multiplication properties and the distributive law in a clear and practical way. The step-by-step solutions make fast calculations and error correction easier. Regular practice strengthens numerical accuracy and logical reasoning. Overall, these solutions build a strong base for algebra and higher mathematics.
NCERT Solutions for Class 8 Maths Chapter 6 - We Distribute, Yet Things Multiply
In the world of mathematics, 4 × 5 is the same as 5 × 4. Also, (2 × 3) × 4 or 2 × (3 × 4); either way, it will provide the same result. Math is cool when you can change the order and still get the same answer. In Class 8 Maths NCERT Chapter 6, 'We Distribute, Yet Things Multiply', students will learn about various properties of multiplication, such as commutative, associative, and distributive properties, among others. These NCERT Solutions for Class 8 serve as a helpful guide, enabling students to verify their answers and understand how to solve each question step by step.
This Story also Contains
- NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Download Free PDF
- NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Exercise Questions
- NCERT We Distribute, Yet Things Multiply Class 8 Chapter 6 Solutions: Topics
- Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply Solutions: Extra Questions
- NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Notes
- NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Important Formulae
- Why are Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply Question Answers Important?
- NCERT Solutions for Class 8 Mathematics Chapter Wise
- NCERT Books and the NCERT Syllabus
This chapter teaches you a smart way to multiply. Teachers often use NCERT content to design their lesson plans. Prepared by Careers360 subject matter experts who have multiple years of experience in this field, these NCERT solutions for class 8 Maths follow the latest syllabus and help you learn better and faster. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus. Explore the full syllabus, detailed explanations, and all solved questions in one place on the Careers360 website.
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Download Free PDF
Careers360 brings you NCERT Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Exercise Questions
NCERT Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply question answers with detailed explanations are provided below.
|
We Distribute, Yet Things Multiply Class 8 Question answers Figure it Out Page number: 142-143 |
Question 1. Observe the multiplication grid below. Each number inside the grid is formed by multiplying two numbers. If the middle number of a 3 × 3 frame is given by the expression pq, as shown in the figure, write the expressions for the other numbers in the grid.
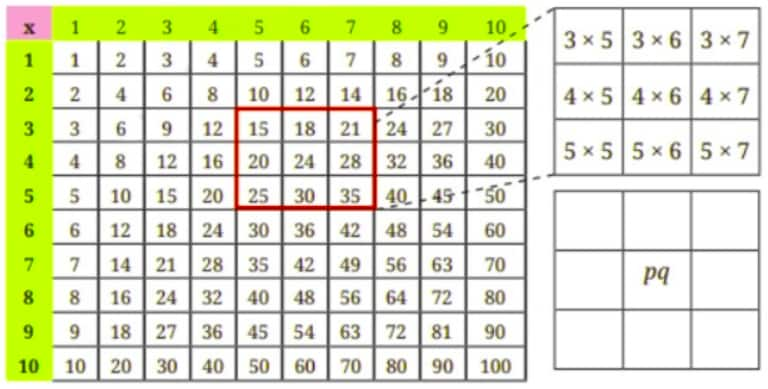
Answer:
|
|
|
|
|
|
|
|
|
|
|
|
Question 2. Expand the following products.
(i) $(3+u)(v-3)$
(ii) $\frac{2}{3}(15+6 a)$
(iii) $(10 a+b)(10 c+d)$
(iv) $(3-x)(x-6)$
(v) $(-5 a+b)(c+d)$
(vi) $(5+z)(y+9)$
Answer:
(i) $(3+u)(v-3)$
$=3 v-9+u v-3 u$
$=u v+3 v-3 u-9$
(ii) $\frac{2}{3}(15+6 a)$
$=\frac{2}{3} \times 15+\frac{2}{3} \times 6 a$
$=10+4 a$
(iii) $(10 a+b)(10 c+d)$
$=100 a c+10 a d+10 b c+b d$
(iv) $(3-x)(x-6)$
$=3 x-18-x^2+6 x$
$=-x^2+9 x-18$
(v) $(-5 a+b)(c+d)$
$=-5 a c-5 a d+b c+b d$
(vi) $(5+z)(y+9)$
$=5 y+45+z y+9 z$
$=5 y+z y+9 z+45$
Question 3. Find 3 examples where the product of two numbers remains unchanged when one of them is increased by 2, and the other is decreased by 4.
Answer:
Let the two numbers be x and y.
According to the question,
$x \times y=(x+2)(y-4)$
$⇒x y=x y-4 x+2 y-8$
$⇒4 x-2 y=-8$
$⇒2 x-y=-4$
$⇒y=2 x+4$
Examples:
1. If $x=1,$ then $y=6 \rightarrow 1 \times 6=6$ and (3) $\times(2)=6$
It satisfies the condition.
2. If $x=2,$, then $y=8 \rightarrow 2 \times 8=16$ and (4) $\times(4)=16$
It satisfies the condition.
3. If $x=5,$ then $y=14 \rightarrow 5 \times 14=70$ and $(7) \times(10)=70$
It satisfies the condition.
Question 4. Expand (i) $\left(a+a b-3 b^2\right)(4+b)$, and (ii) $(4 y+7)(y+11 z-3)$.
Answer:
(i) $\left(a+a b-3 b^2\right)(4+b)$
$=a(4+b)+a b(4+b)-3 b^2(4+b)$
$=4 a+a b+4 a b+a b^2-12 b^2-3 b^3 $
$=4 a+5 a b+a b^2-12 b^2-3 b^3$
(ii) $(4 y+7)(y+11 z-3)$
$=4 y(y+11 z-3)+7(y+11 z-3) $
$=4 y^2+44 y z-12 y+7 y+77 z-21 $
$=4 y^2+44 y z-5 y+77 z-21$
Question 5. Expand (i) $(a-b)(a+b)$, (ii) $(a-b)\left(a^2+a b+b^2\right)$ and (iii) $(a-b)\left(a^3+a^2 b+a b^2+b^3\right)$, Do you see a pattern? What would be the next identity in the pattern that you see? Can you check it by expanding?
Answer:
(i) $(a-b)(a+b)$
$=a^2-b^2$
(i) $(a-b)\left(a^2+a b+b^2\right)$
$=a^3+a^2 b+a b^2-a^2 b-a b^2-b^3$
$=a^3-b^3$
(iii)
$(a-b)\left(a^3+a^2 b+a b^2+b^3\right)$
$=a^4+a^3 b+a^2 b^2+a b^3-a^3 b-a^2 b^2-a b^3-b^4$
$=a^4-b^4$
Here is a clear pattern.
Results are in the form, $a^n -b^n,$ where $n = 2,3,4,...$
So, the next identity:
$(a-b)\left(a^4+a^3 b+a^2 b^2+a b^3+b^4\right)=a^5-b^5$
|
We Distribute, Yet Things Multiply Class 8 Question answers Figure it Out Page number: 149 |
Question 1. Which is greater: $(a-b)^2$ or $(b-a)^2$ ? Justify your answer.
Answer:
$(b-a)^2=[-(a-b)]^2=(-1)^2(a-b)^2=(a-b)^2 $
So they are equal for every $a, b$.
Squaring removes the (-) sign, so the two expressions are identical.
Example:
$(4-2)^2=(2-4)^2=4$
Question 2. Express 100 as the difference of two squares.
Answer:
We know that $x^2-y^2=(x-y)(x+y)$
If $x=26$ and $y=24$,
$26^2-24^2=(26+24)(26-24)=50\times2=100$
If $x=10$ and $y=0$
Then, $(10+0)(10-0)=10^2-0^2=100$
Question 3. Find $406^2, 72^2, 145^2, 1097^2$, and $124^2$ using the identities you have learnt so far.
Answer:
We know that,
$(a+b)^2=a^2+2ab+b^2$
and $(a-b)^2=a^2-2ab+b^2$
(i) $406^2=(400+6)^2=400^2+2 \times 400 \times6+6^2=160000+4800+36=164836$
(i) $72^2=(70+2)^2=70^2+2\times 70 \times2+2^2=4900+280+4=5184$
(iii) $145^2=(150-5)^2=150^2-2\times 150 \times 5+5^2=22500-1500+25=21025$
(iv) $1097^2=(1100-3)^2=1100^2-2\times1100 \times3+3^2=1210000-6600+9=1203409$
(v) $124^2=(100+24)^2=10000+2 \times100 \times 24+24^2=10000+4800+576=15376$
Question 4. Do Patterns 1 and 2 hold only for counting numbers? Do they hold for negative integers as well? What about fractions? Justify your answer.
Answer:
Pattern 1:
$\begin{aligned} & (a+b)^2=a^2+2 \mathrm{ab}+b^2 \\ & (a-b)^2=a^2-2 \mathrm{ab}+b^2\end{aligned}$
Pattern 2:
$a^2-b^2=(a+b) \times(a-b)$
These are algebraic identities that hold not only for counting numbers, but also for
- Negative integers
- Fractions (rational numbers)
- Decimals, irrationals, even complex numbers
Negative numbers check:
Let $a=-3, b=5$ :
Pattern 1:
$(a+b)^2=(2)^2=4$,
RHS $=9-30+25=4$
Pattern 2:
$a^2-b^2=9-25=-16,$
RHS $=(a+b)(a-b)=(2)(-8)=-16$
Fractions check:
Let $a=\frac{1}{2}, b=-\frac{1}{3}$ :
Pattern 1:
$(a-b)^2=\left(\frac{1}{2}+\frac{1}{3}\right)^2=\left(\frac{5}{6}\right)^2=\frac{25}{36}$
RHS $ =\frac{1}{4}+\frac{1}{3}+\frac{1}{9}=\frac{25}{36}$
Pattern 2:
$a^2-b^2=\frac{1}{4}-\frac{1}{9}=\frac{5}{36}$
RHS $=(a+b)(a-b)=\frac{1}{6} \times \frac{5}{6}=\frac{5}{36}$
|
We Distribute, Yet Things Multiply Class 8 Question answers Figure it Out Page number: 151-156 |
Question 1. Compute these products using the suggested identity.
(i) $46^2$ using Identity 1 A for $(a+b)^2$
(ii) $397 \times 403$ using Identity 1 C for $(a+b)(a-b)$
(iii) $91^2$ using Identity 1 B for $(a-b)^2$
(iv) $43 \times 45$ using Identity 1 C for $(a+b)(a-b)$
Answer:
(i)
Lets take $a=40, b=6$ :
$46^2=(40+6)^2=40^2+2 \times 40 \times 6+6^2=1600+480+36=2116$
(ii)
Lets take $a=400, b=3$ :
$397 \times 403=(400-3)(400+3)=400^2-3^2=160000-9=159991$
(iii)
Lets take $a=100, b=9$ :
$91^2=(100-9)^2=10000-2 \cdot 100 \cdot 9+9^2=10000-1800+81=8281$
(iv)
Here $a=44, b=1$:
$43 \times 45=(44-1)(44+1)=44^2-1^2=1936-1=1935$
Question 2. Use either a suitable identity or the distributive property to find each of the following products.
(i) $(p-1)(p+11)$
(ii) $(3 a-9 b)(3 a+9 b)$
(iii) $-(2 y+5)(3 y+4)$
(iv) $(6 x+5 y)^2$
(v) $\left(2 x-\frac{1}{2}\right)^2$
(vi) $(7 p) \times(3 r) \times(p+2)$
Answer:
(i) $(p-1)(p+11)$
Using distributive property:
$=p^2+11 p-p-11$
$=p^2+10 p-11$
(ii) $(3 a-9 b)(3 a+9 b)$
Using Difference of Squares:
$=(3 a)^2-(9 b)^2$
$=9 a^2-81 b^2$
(iii) $-(2 y+5)(3 y+4)$
$=-[(2 y)(3 y)+(2 y)(4)+(5)(3 y)+(5)(4)]$
$=-[6 y^2+8 y+15 y+20]$
$=-[6 y^2+23 y+20]$
$=-6 y^2-23 y-20$
(iv) $(6 x+5 y)^2$
Using the square of sum:
$=(6 x)^2+2(6 x)(5 y)+(5 y)^2$
$=36 x^2+60 x y+25 y^2$
(v) $\left(2 x-\frac{1}{2}\right)^2$
Using the square of difference:
$=(2 x)^2-2(2 x)\left(\frac{1}{2}\right)+\left(\frac{1}{2}\right)^2$
$=4 x^2-2 x+\frac{1}{4}$
(vi) $(7 p) \times(3 r) \times(p+2)$
Using stepwise multiplication:
$=21 p r(p+2)$
$=21 p^2 r+42 p r$
Question 3. For each statement, identify the appropriate algebraic expression(s).
(i) Two more than a square number.
$2+s \quad(s+2)^2 \quad s^2+2 \quad s^2+4 \quad 2 s^2 \quad 2^2 s$
(ii) The sum of the squares of two consecutive numbers
$\begin{array}{llll}m^2+n^2 & (m+n)^2 & m^2+1 \quad m^2+(m+1)^2 \\ m^2+(m-1)^2 & (m+(m+1))^2 & (2 m)^2+(2 m+1)^2\end{array}$
Answer:
(i)
Let a number be $x$.
According to the question,
$s^2+2$
Hence, the correct answer is $s^2+2$.
(ii)
Let the first number be $m$, so the next is $m+1$.
According to the question,
$m^2+(m+1)^2$
Hence, the correct answer is $m^2+(m+1)^2$.
Question 4. Consider any 2 by 2 square of numbers in a calendar, as shown in the figure.
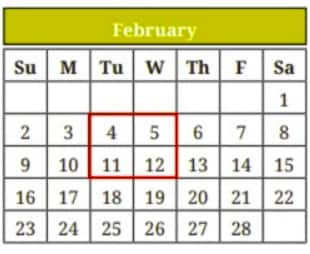
Find products of numbers lying along each diagonal $-4 \times 12=48$, $5 \times 11=55$. Do this for the other 2 by 2 squares. What do you observe about the diagonal products? Explain why this happens.
Hint: Label the numbers in each 2 by 2 square as
|
|
|
|
|
|
Answer:
1st example:
|
|
|
|
|
|
Products of diagonals are:
$2\times10=20$ and $3\times9=27$
2nd example:
|
|
|
|
|
|
Products of diagonals are:
$7\times15=105$ and $8\times 14=112$
We can see that the second diagonal product is always 7 more than the first.
If we take the 1st number as a, then the table becomes:
|
|
|
|
|
|
Product of diagonals:
$a(a+8)=a^2+8a$
And $(a+1)(a+8)=a^2+a+8a+8=a^2+9a+8$
$\text { Difference }=\left[a^2+8 a+7\right]-\left[a^2+8 a\right]=7$
7 is the step size down a column in our grid, so the difference between diagonal products is constant.
Question 5. Verify which of the following statements are true.
(i) $(k+1)(k+2)-(k+3)$ is always 2.
(ii) $(2 q+1)(2 q-3)$ is a multiple of 4.
(iii) Squares of even numbers are multiples of 4, and squares of odd numbers are 1 more than multiples of 8.
(iv) $(6 n+2)^2-(4 n+3)^2$ is 5 less than a square number.
Answer:
(i) $(k+1)(k+2)-(k+3)$
$=k^2+3 k+2-(k+3)$
$=k^2+2 k-1$,
which is not constant 2.
Hence, the statement is False.
(ii) $(2 q+1)(2 q-3)$ is a multiple of 4 .
$=4 q^2-4 q-3$
$=4\left(q^2-q\right)-3$
It is not a multiple of 4 as there is an extra (-3).
Hence, the statement is False.
(iii) Squares of even numbers are multiples of 4, and squares of odd numbers are 1 more than multiples of 8.
Let's take an example.
Let number $=2 m$. Square $=(2 m)^2=4 m^2$, which is a multiple of 4.
Let number $=2 m+1$. Square $=(2 m+1)^2=4m^2+4m+1=4 m(m+1)+1$.
Since $m(m+1)$ is even, we can write $m(m+1)=2 t$,
so square $=8 t+1$. That is 1 more than a multiple of 8.
Hence, the statement is True.
(iv) $(6 n+2)^2-(4 n+3)^2$ is 5 less than a square number.
$(6 n+2)^2-(4 n+3)^2$
$=(6 n+2-4 n-3)(6 n+2+4 n+3)$
$=(2 n-1)(10 n+5)$
$=5(2 n-1)(2 n+1)$
$=20 n^2-5 $
$20n^2$ is not a square number for any values of $n$.
Hence, the statement is False.
Question 6. A number leaves a remainder of 3 when divided by 7, and another number leaves a remainder of 5 when divided by 7. What is the remainder when their sum, difference, and product are divided by 7?
Answer:
The 1st number = $7+3=10$
and 2nd number $=7+5=12$
Sum = 10 + 12 = 22, when divided by 7 leaves a remainder of 1.
Difference = 10 - 12 = - 2, when divided by 7 leaves a remainder of 5.
[In this case, we will use the definition of division with remainder for negative numbers.
The largest multiple of 7 less than or equal to -2 is -7. This is because $7 \times-1=-7$
So, remainder $=-2-(-7)=-2+7=5$]
Product = $10\times12=120$, when divided by 7 leaves a remainder of 1.
Question 7. Choose three consecutive numbers, square the middle one, and subtract the product of the other two. Repeat the same with the other sets of numbers. What pattern do you notice? How do we write this as an algebraic equation? Expand both sides of the equation to check that it is a true identity.
Answer:
Let three consecutive numbers be $n-1, n, n+1$.
According to the question,
$n^2-(n-1)(n+1)=n^2-\left(n^2-1\right)=1$
Other example:
Let three consecutive numbers be $n+1, n+2, n+3$.
$(n+2)^2-(n+1)(n+3)=n^2+4n+4-n^2-n-3n-3=1$
The Pattern shows that the result is always 1.
Algebraic identity: $n^2-(n-1)(n+1)=1$.
Expanding both sides shows it is true.
Question 8. What is the algebraic expression describing the following steps:
Add any two numbers. Multiply this by half of the sum of the two numbers? Prove that this result will be half of the square of the sum of the two numbers.
Answer:
Let the two numbers be $x$ and $y$.
According to the question,
$(x+y) \times \frac{1}{2}(x+y)$
$=\frac{1}{2}(x+y)^2$
So the result equals half the square of the sum.
Now,
$\frac{1}{2}\left(x^2+2 x y+y^2\right)$
$=\frac{1}{2} x^2+x y+\frac{1}{2} y^2$
which matches the direct expansion.
Question 9. Which is larger? Find out without fully computing the product.
(i) $14 \times 26$ or $16 \times 24$
(ii) $25 \times 75$ or $26 \times 74$
Answer:
(i)
$14 \times 26$
$=(20-6)(20+6)$
$=20^2-6^2$
$16 \times 24$
$=(20-4)(20+4)$
$=20^2-4^2$
So, clearly $16 \times 24$ is larger.
(ii)
$25 \times 75$
$=(50-25)(50+25)$
$=50^2-25^2$
$26 \times 74$
$=(50-24)(50+24)$
$=50^2-24^2$
So, clearly $26 \times 74$ is larger.
Question 10. A tiny park is coming up in Dhauli. The plan is shown in the figure. The two square plots, each of area $g^2$ sq. ft, will have a green cover. All the remaining area is a walking path $w$ ft . wide that needs to be tiled. Write an expression for the area that needs to be tiled.
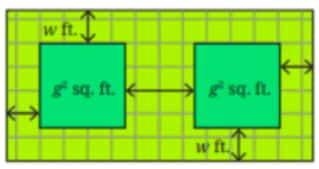
Answer:
Outer rectangle width(From left) $=w+g+w+g+w=2 g+3 w$
Outer rectangle height(From Up to Down) $=w+g+w=g+2 w$
Total outer area $=(2 g+3 w)(g+2 w)=2g^2+3gw+4gw+6w^2=2g^2+6w^2+7gw$
Green area (two squares) $=g^2+g^2=2 g^2$
$\therefore$ Required area that needs to be tiled = $2g^2+6w^2+7gw-2g^2=6w^2+7gw=w(6w+7g)$
Question 11. For each pattern shown below,
(i) Draw the next figure in the sequence.
(ii) How many basic units are there in Step 10?
(iii) Write an expression to describe the number of basic units in Step $y$.
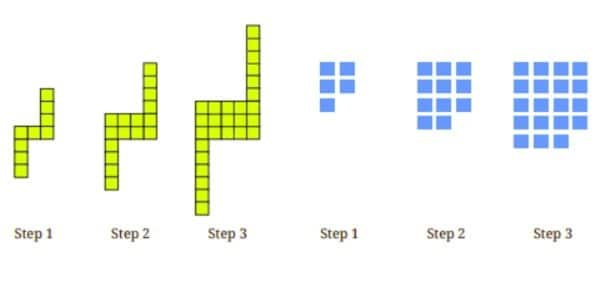
Answer:
(i)
1st pattern:
Step 1: 9 units
Step 2: 16 units
Step 3: 27 units
Differences between terms: $+7,+11,+15, \ldots$ (increase by 4 ).
nth term: $a_n=2 n^2+n+6$, where $n=1,2,3,...$
4th term: $a_4=2\times 4^2+4+6=42$
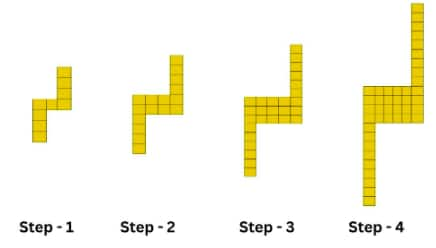
(ii)
10th term: $a_{10}=2\times(10)^2+10+6=216$
(iii)
yth term: $a_y=2 y^2+y+6$, where $y=1,2,3,...$
(i)
2nd pattern:
Step 1: 5 units
Step 2: 11 units
Step 3: 19 units
Differences: $+6,+8,+10, \ldots$ (increase by 2 ).
nth term: $b_n=n^2+3 n+1$, where $n=1,2,3,....$
4th term: $b_4=4^2+3\times4+1=29$
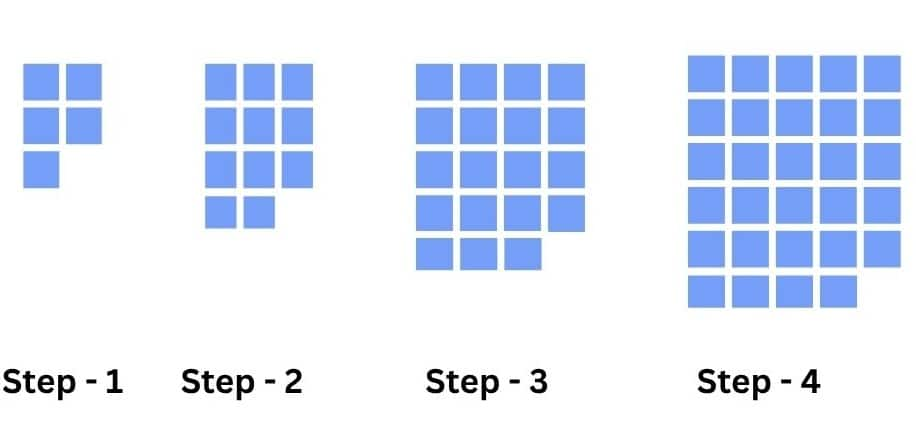
(ii)
10th term: $b_{10}=10^2+3\times(10)+1=131$
(iii)
yth term: $b_y=y^2+3 y+1$, where $y=1,2,3,....$
NCERT We Distribute, Yet Things Multiply Class 8 Chapter 6 Solutions: Topics
Students will explore the following topics in NCERT Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply:
- Some Properties of Multiplication
- Fast Multiplications Using the Distributive Property
- Special Cases of the Distributive Property
- Mind the Mistake, Mend the Mistake
- This Way or That Way, All Ways Lead to the Bay
Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply Solutions: Extra Questions
Question 1:
Simplify using the distributive property:
12 × (15 – 7) + 8 × (15 – 7)
Solution:
Both terms have (15 – 7).
So, we can apply the distributive property:
12 × (15 – 7) + 8 × (15 – 7)
= (12 + 8) × (15 – 7)
= 20 × (8)
= 160
Hence, the correct answer is 160.
Question 2:
If the number p is 5 more than q and the sum of the square of p and q is 55, then the product of p and q is:
Solution:
$
\begin{aligned}
& \text { Given: } p=q+5 \\
& \Rightarrow p-q=5 \\
& \text { Also, } p^2+q^2=55 \\
& \Rightarrow p^2+q^2-2 p q+2 p q=55 \\
& \Rightarrow(p-q)^2+2 p q=55 \\
& \Rightarrow 25+2 p q=55 \\
& \Rightarrow 2 p q=30 \\
& \therefore p q=15
\end{aligned}
$
Hence, the correct answer is 15.
Question 3:
Find $48 \times 7$ using the distributive property.
Solution:
$
\begin{gathered}
48=40+8 \\
48 \times 7=(40+8) \times 7 \\
=40 \times 7+8 \times 7 \\
=280+56=336
\end{gathered}
$
Hence, the correct answer is 336.
Question 4:
Find $99 \times 8$ using a special case of the distributive property.
Solution:
$\begin{gathered}99=100-1 \\ (100-1) \times 8=800-8=792\end{gathered}$
Hence, the correct answer is 792.
Question 5:
A student calculated $25 \times 6=25 \times(5+1)=150+6=156$. Correct the mistake.
Solution:
$\begin{gathered}25 \times(5+1)=25 \times 5+25 \times 1 \\ =125+25=150\end{gathered}$
Hence, the correct answer is 150.
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Notes
Careers360 has prepared these Class 8 We Distribute, Yet Things Multiply Notes to make your revision smoother and faster. Additionally, these notes will help students to understand the We Distribute, Yet Things Multiply NCERT solutions and solve them on their own from next time.
Properties of multiplication
Distributive Property of Multiplication
The distributive property states that when you multiply a number by a sum (or difference), you can distribute the multiplication to each term inside the parentheses and then add (or subtract) the results.
Example:
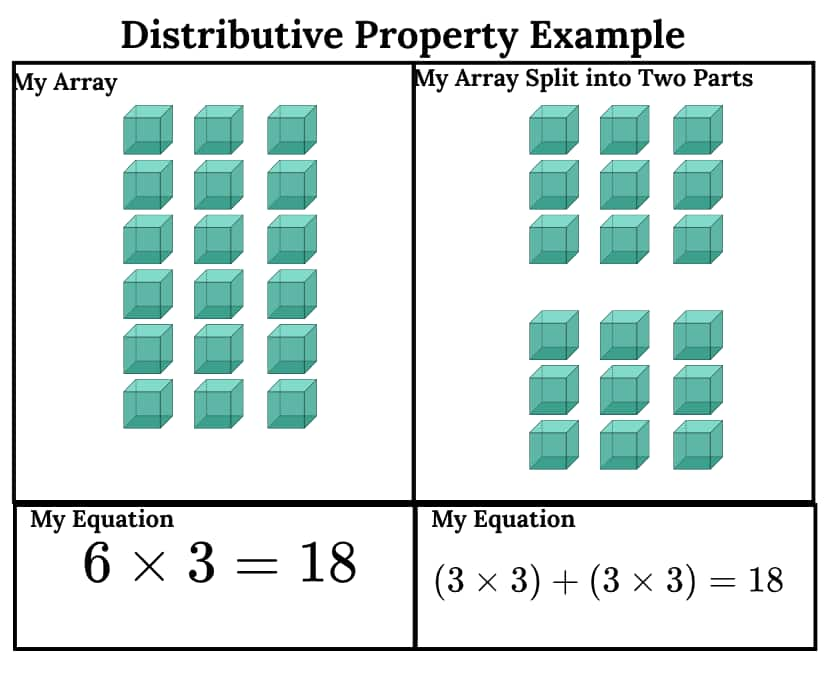
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Important Formulae
- $(a+b)^2=a^2+2 \mathrm{ab}+b^2$
- $(a-b)^2=a^2-2 \mathrm{ab}+b^2$
- $a^2-b^2=(a+b) \times(a-b)$
- $(a+b)(c+d)=a c+a d+b c+b d$
- $(k \cdot m)^2=k^2 \cdot m^2$
- If numbers are $n+1, n+2, n+3$, then: $(n+2)^2-(n+1)(n+3)=1$
Why are Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply Question Answers Important?
The 6th chapter in class 6, “We Distribute, Yet Things Multiply”, teaches us how multiplication works in different ways using smart tricks and rules. It also helps students learn to multiply faster, avoid common mistakes, and understand how numbers behave. These Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply question answers make these concepts simple and useful for daily problem-solving. Here are some more points on why they are important:
- These solutions explain important properties of multiplication clearly, helping you understand how numbers relate to each other.
- These exercises on fast multiplication using the distributive property make solving sums quicker and easier.
- These lessons prepare you for algebra and higher maths topics where distributive and special cases are often used.
- Practising Class 8 Maths We Distribute, Yet Things Multiply question answers help you spot and correct mistakes while building confidence in solving problems.
NCERT Solutions for Class 8 Mathematics Chapter Wise
For students' preparation, Careers360 has gathered all Class 8 Maths NCERT solutions here for quick and convenient access.
|
NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube |
|
NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers |
|
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply |
|
NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning-1 |
NCERT Books and the NCERT Syllabus
The links below will help you access the NCERT books and the complete NCERT syllabus for Class 8 quickly and easily.
Frequently Asked Questions (FAQs)
Q: What is the main topics covered in Chapter 6 "We Distribute, Yet Things Multiply"?
A:
This chapter deals with concepts such as:
- Distributive property of multiplication over addition and subtraction
- Some algebraic identities
- Some patterns related to multiplication
Q: Why is the chapter titled "We Distribute, Yet Things Multiply"?
A:
The title reflects the idea of the distributive property, where multiplication is distributed over addition or subtraction, resulting in expressions that look like multiplication has increased or multiplied terms, yet it’s just distribution.
Q: Are there any important formulas or rules in this chapter?
A:
The key formula in this chapter is the distributive property formula.
a (b + c) = ab + ac
and a(b - c) = ab - ac
Q: Where can I find the NCERT solutions for Chapter 6?
A:
NCERT Solutions for Class 8 Chapter 6 can be found on various educational websites such as Careers360. In Careers360, these solutions are written in a step-by-step manner to help students understand the solution technique.
Q: What kind of exercises are included in the NCERT textbook for this chapter?
A:
Exercises include expanding algebraic expressions, simplifying them, factoring by taking common terms, and applying these concepts in word problems and pattern-based questions.
Q: Can the distributive property be applied to decimals?
A:
Yes. Example: 1.2 × 3.5 = (1 × 3.5) + (0.2 × 3.5) = 3.5 + 0.7 = 4.2
Q: How do we multiply numbers near multiples of 10, 100, or 1000?
A:
We break the numbers using the distributive property:
Example: 102 × 5 = (100+2) × 5 = 500 + 10 = 510
Q: What kind of mistakes are common in multiplication?
A:
Common mistakes of this chapter include:
Misplacing digits
Forgetting to carry numbers
Wrong addition after distributing
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters