NCERT Solutions for Class 8 Maths Chapter 5 - Number Play
Do you know if the last three digits are divisible by 8, then the whole number is divisible by 8? Or if a number is divisible by both 2 and 3, it is divisible by 6. Welcome to the playground of numbers, where you will learn about all these and many more. Class 8 Maths NCERT Chapter 5 Number Play is a pivotal chapter as the learning from this chapter is not only helpful in this class but also for higher classes. This chapter also covers topics such as the sum of consecutive numbers, breaking even numbers and problems related to remainders and many more. The primary objective of these NCERT solutions for Class 8 is to provide students with valuable study material for verifying answers and learning how to solve exercise problems.
This Story also Contains
- NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Download Free PDF
- NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Exercise Questions
- NCERT Number Play Class 8 Chapter 5: Topics
- NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Notes
- Class 8 Maths Chapter 5 Number Play Solutions: Extra Question
- NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Important Formulae
- Why are Class 8 Maths Chapter 5 Number Play Question Answers Important?
- NCERT Solutions for Class 8 Mathematics Chapter Wise
- NCERT Books and NCERT Syllabus

A remainder might look small, but it holds great power in mathematical problems. Curated by Careers360 experts, these NCERT solutions for class 8 Maths strictly follow the updated syllabus, ensuring focused and effective learning. These solutions are explained in a step-by-step manner and simple language so that every type of student can understand and learn. Many teachers recommend NCERT Solutions because they closely match the exam pattern. Check this NCERT article for complete syllabus coverage along with NCERT Books, Solutions, Syllabus, and Exemplar Problems with Solutions.
NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Download Free PDF
Careers360 brings you NCERT Class 8 Maths Chapter 5 Number Play solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.
NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Exercise Questions
Below, you will find the NCERT Class 8 Maths Chapter 5 Number Play question answers explained step by step.
|
Figure it Out Page number: 122-123 |
Question 1. The sum of four consecutive numbers is 34. What are these numbers?
Answer:
Let the four numbers be x, x + 1, x + 2, and x+ 3
According to the question,
x + x + 1 + x + 2 + x + 3 = 34
⇒ 4x + 6 = 34
⇒ 4x = 28
⇒ x = 7
So, the numbers are 7, 8, 9, and 10
Question 2. Suppose $p$ is the greatest of five consecutive numbers. Describe the other four numbers in terms of $p$.
Answer:
If $p$ is the greatest, the numbers are:
$p-4, p-3, p-2, p-1$
Question 3. For each statement below, determine whether it is always true, sometimes true, or never true. Explain your answer. Mention examples and non-examples as appropriate. Justify your claim using algebra.
(i) The sum of two even numbers is a multiple of 3.
(ii) If a number is not divisible by 18, then it is also not divisible by 9.
(iii) If two numbers are not divisible by 6, then their sum is not divisible by 6.
(iv) The sum of a multiple of 6 and a multiple of 9 is a multiple of 3.
(v) The sum of a multiple of 6 and a multiple of 3 is a multiple of 9.
Answer:
(i) The sum of two even numbers is a multiple of 3.
Example:
$2+4=6$, multiple of 3
$2+8=10$, not a multiple of 3
This statement is "Sometimes True".
(ii) If a number is not divisible by 18, then it is also not divisible by 9.
Example: 9 is divisible by 9 but not by 18.
This statement is "Never True".
(iii) If two numbers are not divisible by 6, then their sum is not divisible by 6.
- Example: 1 and $5 \rightarrow$ sum $=6$ (divisible by 6)
- Example: 1 and $2 \rightarrow$ sum $=3$ (not divisible by 6)
This statement is "Sometimes True".
(iv) The sum of a multiple of 6 and a multiple of 9 is a multiple of 3.
Example:
Multiple of $6 \rightarrow 6 a$, Multiple of $9 \rightarrow 9 b$
Sum $=6 a+9 b=3(2 a+3 b) \rightarrow$ Always multiple of 3
This statement is "Always True".
(v) The sum of a multiple of 6 and a multiple of 3 is a multiple of 9.
Example: $6+3=9$ [divisible by 9]
Example: $6+6=12 \times$ [not divisible by 9]
This statement is "Sometimes True".
Question 4. Find a few numbers that leave a remainder of 2 when divided by 3 and a remainder of 2 when divided by 4. Write an algebraic expression to describe all such numbers.
Answer:
Let the number be $k$.
When Divided by $3 \rightarrow 3 k+2$
When Divided by $4 \rightarrow 4 m+2$
We need numbers that satisfy both.
LCM of 3 and $4=12$
$\therefore$ The Pattern is: $2,14,26,38, \ldots$
General form: $12 n+2$
Question 5. "I hold some pebbles, not too many, When I group them in 3's, one stays with me. Try pairing them up - it simply won't do, A stubborn odd pebble remains in my view. Group them by 5, yet one's still around, But grouping by seven, perfection is found. More than one hundred would be far too bold, Can you tell me the number of pebbles I hold?"
Answer:
So the number of pebbles leaves a remainder of 1 when ÷3
Leaves remainder 1 when ÷5
Also, the number of pebbles is divisible by 7.
LCM of 3, 5 = 15
So, the number should be 1 more than a multiple of 15.
15 × 1 + 1 = 16 [Not Divisible by 7]
15 × 2 + 1 = 31 [Not Divisible by 7]
15 × 3 + 1 = 46 [Not Divisible by 7]
15 × 4 + 1 = 61 [Not Divisible by 7]
15 × 5 + 1 = 76 [Not Divisible by 7]
15 × 6 + 1 = 91 [Divisible by 7]
Hence, the number of pebbles is 91.
Question 6. Tathagat has written several numbers that leave a remainder of 2 when divided by 6. He claims, "If you add any three such numbers, the sum will always be a multiple of $6$". Is Tathagat's claim true?
Answer:
Numbers that leave a remainder of 2 when divided by 6 are $ 6 k+2$
Sum of three such numbers:
$(6 a+2)+(6 b+2)+(6 c+2)=6(a+b+c+1)$
This is always divisible by 6.
Hence, his claim is True.
Question 7. When divided by 7, the number 661 leaves a remainder of 3, and 4779 leaves a remainder of 5. Without calculating, can you say what remainders the following expressions will leave when divided by 7?
Show the solution both algebraically and visually.
(i) $4779+661$
(ii) $4779-661$
Answer:
Given:
$661 \equiv 3\ (\bmod 7),$ $4779 \equiv 5\ (\bmod 7)$
(i) $4779+661 \equiv 5+3=8 \equiv 1(\bmod 7)$
(ii) $4779-661 \equiv 5-3=2(\bmod 7)$
Question 8. Find a number that leaves a remainder of 2 when divided by 3, a remainder of 3 when divided by 4, and a remainder of 4 when divided by 5. What is the smallest such number? Can you give a simple explanation of why it is the smallest?
Answer:
The required number leaves a remainder of 2 when divided by 3, a remainder of 3 when divided by 4, and a remainder of 4 when divided by 5.
Notice pattern: 3-1 = 4-1 = 5-1 = 2
So, the number is 1 less than a multiple of 60 (LCM 3, 4, and 5)
Hence, the smallest such number is 60 - 1 = 59
It is the smallest number because it is the LCM of 3, 4, and 5. Not a multiple of the LCM.
|
Figure it Out Page number: 126 |
Question 1. Find, without dividing, whether the following numbers are divisible by 9.
(i) 123
(ii) 405
(iii) 8888
(iv) 93547
(v) 358095
Answer:
We know that a number is divisible by 9 if the sum of its digits is divisible by 9.
(i) $123 \rightarrow 1+2+3=6 \rightarrow$ Not divisible by 9
(ii) $405 \rightarrow 4+0+5=9 \rightarrow$ Divisible by 9
(iii) $8888 \rightarrow 8+8+8+8=32 \rightarrow$ Not divisible by 9
(iv) $93547 \rightarrow 9+3+5+4+7=28 \rightarrow$ Not divisible by 9
(v) $358095 \rightarrow 3+5+8+0+9+5=30 \rightarrow$ Not divisible by 9
Question 2. Find the smallest multiple of 9 with no odd digits.
Answer:
If we multiply 9 by odd digits, we will get odd digits as a result.
So, we will multiply 9 by only even digits.
-
$18 $ ( 1 is odd)
-
$36 $ ( 3 is odd)
-
$72 $ ( 7 is odd)
-
$90 $ ( 9 is odd)
-
$108 $ ( 1 is odd)
-
$216 $ ( 1 is odd)
-
$288(2+8+8=18 \rightarrow$ divisible by 9, and digits 2,8,8 are even)
Question 3. Find the multiple of 9 that is closest to the number 6000.
Answer:
$6000 \div 9 \approx 666.67$
So, the Closest multiples are:
$666 \times 9=5994$
$667 \times 9=6003$
Distance:
$6000-5994=6$
$6003-6000=3$
Hence, the answer is 6003.
Question 4. How many multiples of 9 are there between the numbers 4300 and 4400?
Answer:
$4300 \div 9 \approx 477.77 $
$4400 \div 9 \approx 488.8$
So, we have to multiply 9 by 478 to 488 to get the answer.
Hence, the required multiples are $4302,4311,4320,4329,4338,4347,4356,4365,4374,4383,4392$.
|
Figure it Out Page number: 131 |
Question 1. The digital root of an 8-digit number is 5. What will be the digital root of 10 more than that number?
Answer:
The digital root of an 8-digit number is 5.
Now, if we add 10 to that number, 5 + 10 = 15
So, the digital root will be 1 + 5 = 6
Question 2. Write any number. Generate a sequence of numbers by repeatedly adding 11. What would be the digital roots of this sequence of numbers? Share your observations.
Answer:
Let the first number of the sequence be 4.
Digital roots:
-
$4 \rightarrow 4$
-
$15 \rightarrow 1+5=6$
-
$26 \rightarrow 2+6=8$
-
$37 \rightarrow 3+7=10 \rightarrow 1+0=1$
-
$48 \rightarrow 4+8=12 \rightarrow 1+2=3$
-
$59 \rightarrow 5+9=14 \rightarrow 1+4=5$
-
$70 \rightarrow 7+0=7$
-
$81 \rightarrow 8+1=9$
-
$92 \rightarrow 9+2=11 \rightarrow 1+1=2$
-
$103 \rightarrow 1+0+3=4$
-
$114 \rightarrow 1+1+4=6$
We can see that the pattern repeats every 9 terms.
Question 3. What will be the digital root of the number $9 a+36 b+13$?
Answer:
We find the digital root by taking the expression modulo 9 :
-
$9 a \equiv 0(\bmod 9)$
-
$36 \mathrm{~b} \equiv 0(\bmod 9)$
-
$13 \equiv 4(\bmod 9)$
So, $9 a+36 b+13 \equiv 4 \bmod 9$
Hence, the digital root is 4.
Question 4. Make conjectures by examining if there are any patterns or relations between
(i) the parity of a number and its digital root.
(ii) the digital root of a number and the remainder obtained when the number is divided by 3 or 9.
Answer:
(i)
There is no fixed relation between Parity and digital root. Parity and digital root are independent. A number can be even or odd regardless of its digital root.
Example: Even number 14 has a digital root, 1 + 4 = 5, which is odd.
Also, even number 24 has a digital root, 2 + 4 = 6, which is even.
(ii)
The digital root of a number is the same as the remainder when the number is divided by 9, except when the remainder is 0 — in that case, the digital root is 9.
If the digital root is 3, 6, or 9, then the number is divisible by 3.
|
Figure it Out Page number: 132-134 |
Question 1. If $31 z 5$ is a multiple of 9 , where $z$ is a digit, what is the value of $z$ ? Explain why there are two answers to this problem.
Answer:
We know that a number is divisible by 9 if the sum of its digits is divisible by 9.
Given number: 31z5
Sum of the digits apart from z is 3 + 1 + 5 = 9
So, if we put z = 0, we get 3105, which is divisible by 9 as the sum of the digits is 9.
If we put z = 9, we get 3195, which is also divisible by 9, as the sum of the digits is 18, which is divisible by 9.
We get two answers because both values make the digit sum a multiple of 9.
Question 2. "I take a number that leaves a remainder of 8 when divided by 12. I take another number, which is 4 short of a multiple of 12. Their sum will always be a multiple of 8", claims Snehal. Examine his claim and justify your conclusion.
Answer:
1st number = 12k + 8
2nd number = 12k - 4
Sum = 12k + 8 + 12k - 4 = 24k + 4
According to Snehal, it is always a multiple of 8.
If we put k = 1, 24 × 1 + 4 = 24, which is a multiple of 8.
k = 2, 24 × 2 + 4 = 48, which is a multiple of 8.
k = 3, 24 × 3 + 4 = 76, which is not a multiple of 8.
So, her claim is “Sometimes True”.
Question 3. When is the sum of two multiples of 3, a multiple of 6 and when is it not? Explain the different possible cases, and generalise the pattern.
Answer:
Let the two numbers be $3 a$ and $3 b$ (multiples of 3)
$\text { Sum }=3 a+3 b=3(a+b)$
This is always divisible by 3.
But it's divisible by 6 only if the value of (a + b) is even.
So, we can conclude that
-
If $a+b$ is even $\rightarrow$ sum divisible by 6
-
If $a+b$ is odd $\rightarrow$ sum not divisible by 6
Question 4. Sreelatha says, "I have a number that is divisible by 9. If I reverse its digits, it will still be divisible by 9 ".
(i) Examine if her conjecture is true for any multiple of 9.
(ii) Are any other digit shuffles possible such that the number formed is still a multiple of 9?
Answer:
(i) We know that a number is divisible by 9 if the sum of its digits is divisible by 9.
So, if we reverse the digits of a number which a multiple of 9, then it will still be divisible by 9 as the sum of the digits remains the same.
Example:
117 is divisible by 9, as well as 711 and 171.
(ii)
As long as the sum of digits remains the same, any shuffle will work.
Question 5. If $48 a 23 b$ is a multiple of 18, list all possible pairs of values for $a$ and $b$.
Answer:
LCM of 2 and 9 is 18.
So if the number is divisible by 2 and 9, then it is divisible by 18.
A number is divisible by 2 if the last digit is even or 0.
A number is divisible by 9 if the sum of its digits is divisible by 9.
In 48a23b, the sum of the digits apart from a and b is 4+8+2+3 = 17
So if a = 1 and b = 0, the number becomes 481230, which is divisible by both 2 and 9; thus divisible by 18.
No more values can be obtained.
So the values of a and b are 1 and 0, respectively.
Question 6. If $3 p 7 q 8$ is divisible by 44, list all possible pairs of values for $p$ and $q$.
Answer:
LCM of 4 and 11 is 44.
So if a number is divisible by 4 and 11, then it is divisible by 44.
If the last two digits of a number are divisible by 4, then the whole number is divisible by 4.
A number is divisible by 11 if the difference between the sum of its digits in odd places and the sum of its digits in even places is either 0 or divisible by 11.
So, (3+7+8)-(p+q) = 18-p-q must be divisible by 11 or 0.
If the values of p = 7 and q = 0, then the number becomes 37708, which is divisible by both 4 and 11; thus divisible by 44.
Also, values that are possible:
p = 5, q = 2;
p = 3, q = 4;
p = 1, q = 6;
Question 7. Find three consecutive numbers such that the first number is a multiple of 2, the second number is a multiple of 3, and the third number is a multiple of 4. Are there more such numbers? How often do they occur?
Answer:
The first set of numbers which satisfies the conditions is 14, 15, 16.
LCM of 2, 3, and 4 = 12
If we add 12 to the first number, then the sequence repeats.
So, the next such sets are:
14, 15, 16
26, 27, 28
38, 39, 40
50, 51, 52
And so on
Question 8. Write five multiples of 36 between 45,000 and 47,000. Share your approach with the class.
Answer:
Step:
Divided 45000 by 36.
We will get 1250.
Now, to get the multiple between 45000 and 47000, we have to multiply 36 by more than 1250.
So, the five multiples of 36 between 45,000 and 47,000 are:
36 × 1251 = 45036
36 × 1252 = 45072
36 × 1253 = 45108
36 × 1254 = 45144
36 × 1255 = 45180
Question 9. The middle number in the sequence of 5 consecutive even numbers is $5 p$. Express the other four numbers in sequence in terms of $p$.
Answer:
The middle number in the sequence of 5 consecutive even numbers is $5 p$.
So, the other numbers in that sequence are:
$5p-2,5p-4,5p+2,5p+4$
Question 10. Write a 6 -digit number that it is divisible by 15, such that when the digits are reversed, it is divisible by 6.
Answer:
LCM of 3 and 5 is 15.
So if a number is divisible by both 3 and 5, then the number is divisible by 15.
A number is divisible by 3 if the sum of its digits is divisible by 3.
If the last digit of a number is 0 or 5, then the number is divisible by 5.
For the reverse number to be divisible by 6, it has to be divisible by 2 and 3.
So the first digit should be even, and the sum of the digits should be divisible by 3.
Let's try 234105..
Here, some of the digits are 15, the last digit is 5, and in reverse order, the last digit is even.
So it satisfies all the conditions.
Question 11. Deepak claims, "There are some multiples of 11 which, when doubled, are still multiples of 11. But other multiples of 11 don't remain multiples of 11 when doubled". Examine if his conjecture is true; explain your conclusion.
Answer:
Let's check Dipak’s hypothesis.
11 × 2 = 22
Now, the multiples of 22, such as 44, 66, 88, are all multiples of 11.
11 × 3 = 33
Now, the multiples of 33, such as 66, 99, 132, are all multiples of 11.
So, Deepak’s claim is not correct.
All doubled multiples of 11 are still multiples of 11.
Question 12. Determine whether the statements below are 'Always True', 'Sometimes True', or 'Never True'. Explain your reasoning.
(i) The product of a multiple of 6 and a multiple of 3 is a multiple of 9.
(ii) The sum of three consecutive even numbers will be divisible by 6.
(iii) If abcdef is a multiple of 6, then badcef will be a multiple of 6.
(iv) $8(7 b-3)-4(11 b+1)$ is a multiple of 12 .
Answer:
(i) The product of a multiple of 6 and a multiple of 3 is a multiple of 9.
This statement is "Sometimes True".
Ex: $6 \times 3=18$, is a multiple of 9,
but $6 \times 9=54$ (not a multiple of 9 )
(ii) Sum of 3 consecutive even numbers divisible by 6.
Example:
$2 n, 2 n+2,2 n+4 \rightarrow$ sum $=6 n+6=6(n+1)$
This statement is "Always True".
(iii) If abcdef is divisible by 6, is badcef also divisible by 6.
To be divisible by 6, it has to be divisible by 2 and 3.
So, abcdef is already divisible by 6.
So f is even and the sum of the digits is divisible by 3.
If we reverse it without changing the last digit, then the sum remains the same and the last digit is still even.
So it is divisible by 6.
This statement is "Always True".
(iv) $8(7 b-3)-4(11 b+1)$ is a multiple of 12.
$8(7 b-3)-4(11 b+1)=56b-24-44b-4=12b-28$
If b is 1, it becomes -16, which is not divisible by 12.
This statement is "Never True".
Question 13. Choose any 3 numbers. When is their sum divisible by 3? Explore all possible cases and generalise.
Answer:
-
$3,6,9 \rightarrow$ sum $=18 \rightarrow$ Divisible by 3
-
$1,2,3 \rightarrow$ sum $=6 \rightarrow$ Divisible by 3
-
$1,2,4 \rightarrow$ sum $=7\rightarrow$ Not Divisible by 3
The sum of 3 numbers is divisible by 3 if their total sum is divisible by 3
So if all numbers leave the same remainder mod 3 (like $1,4,7$ ), or their remainders sum to 3 or 6, the result is divisible by 3.
Question 14. Is the product of two consecutive integers always a multiple of 2? Why? What about the product of these consecutive integers? Is it always a multiple of 6? Why or why not? What can you say about the product of 4 consecutive integers? What about the product of five consecutive integers?
Answer:
Yes, the product of two consecutive integers is always a multiple of 2.
Product of two consecutive numbers: n(n+1)
If n even → even × odd = even
If n odd → odd × even = even
No, it sometimes can be divisible by 6, if the last digits are even and the sum of the digits is divided by 3.
2 × 3 = 6 [Divisible by 6]
3 × 4 = 12 [Divisible by 6]
4 × 5 = 20 [Not divisible by 6]
The product of 4 consecutive integers is divisible by 24.
The product of 5 consecutive integers is divisible by 120.
Question 15. Solve the cryptarithms -
(i) $\mathrm{EF} \times \mathrm{E}=\mathrm{GGG}$
(ii) $\mathrm{WOW} \times 5=\mathrm{MEOW}$
Answer:
(i)
$\mathrm{EF} \times \mathrm{E}=\mathrm{GGG}$
⇒ 10E + F × E = 100 G + 10G + G
⇒ (10E + F) × E = 111G
If E = 1, then 10 + F = 111G
[It is not possible because for any value of F, LHS can't be equal to RHS]
If E = 2, then (20 + F) × 2 = 111G
[It is also not possible because for any value of F, LHS can't be equal to RHS]
For E = 3, then (30 + F) × 3 = 111G
⇒ 90 + 3F = 111G
If F = 7 and G = 1, then LHS = RHS.
$\therefore$ The values of E, F, and G are 3, 7, and 1, respectively.
(ii)
$\mathrm{WOW} \times 5=\mathrm{MEOW}$
Using the same process as the previous one.
(100W + 10O + W) × 5 = MEOW
⇒ (101 W + 10 O) × 5 = MEOW
⇒ 505 W + 50 O = MEOW
Let’s try possible values of W and O such that the result is a 4-digit number.
If we set W = 5 and O = 7, we obtain a 4-digit number.
505 × 5 + 50 × 7 = 2875
On the right-hand side, if MEOW = 2875
W = 5, O = 7
1000M + 100E + 10O + W = 1000M + 100E + 70 + 5 = 1000M + 100E + 75
If we take M = 2 and E = 8, then it satisfies the LHS.
So, the values of M, E, O, and W are 2, 8, 7, and 5, respectively.
Question 16. Which of the following Venn diagrams captures the relationship between the multiples of 4, 8, and 32?
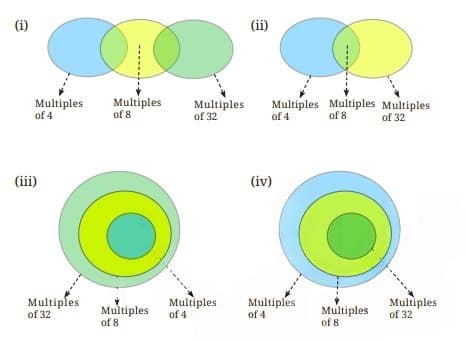
Answer:
The correct answer is option (iv).
Here are the reasons for the answer.
-
Every multiple of 32 is also a multiple of 8 and 4.
-
Every multiple of 8 is also a multiple of 4.
-
But not every multiple of 4 is a multiple of 8 or 32.
NCERT Number Play Class 8 Chapter 5: Topics
Students will explore the following topics in NCERT Class 8 Maths Chapter 5 Number Play:
-
Sum of Consecutive Numbers
-
Breaking Even Numbers
-
Pairs to Make Fours
-
Remainder
-
Checking Divisibility Quickly
-
Digits in Disguise
NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Notes
Careers360 has prepared these Class 8 Number Play Notes to make your revision smoother and faster. Additionally, these notes will help students to understand the Number Play NCERT solutions and solve them on their own from next time.
Divisibility Rules
Divisibility rules are simple tricks or shortcuts that help us check if one number can be divided by another number without leaving a remainder — and we can do it without actually dividing.

Remainder
When we divide one number by another, sometimes the number doesn’t divide evenly.
The leftover part is called the remainder.

Class 8 Maths Chapter 5 Number Play Solutions: Extra Question
Question:
6m61 is divisible by 11. What is the value of m?
Solution:
For divisibility by 11:
The sum of the digits at the even place minus the sum of the odd place should be 0 or divisible by 11.
So, 6 + 6 – m – 1 = 0 or is divisible by 11.
If we put m = 0, then
⇒ 6 + 6 – 1 = 11, which is divisible by 11.
Hence, the correct answer is 0.
NCERT Solutions for Class 8 Maths Chapter 5 Number Play: Important Formulae
-
If the last digit of a number is even (i.e., 0, 2, 4, 6, 8), then the number is divisible by 2.
-
If the sum of the digits of a number is divisible by 3, then that number is divisible by 3.
-
If the last two digits of a number from left to right are divisible by 4, then that number is divisible by 4.
-
If the last digit of a number is 0 or 5, then that number is divisible by 5.
- If a number is divisible by 2 and 3, then that number is divisible by 6.
-
The 7 divisibility rule states that if a number is divisible by 7, then “the difference between twice the unit digit of the given number and the remaining part of the given number should be a multiple of 7 or it should be equal to 0”.
-
If the last three digits of a number from left to right are divisible by 8, then that number is divisible by 8.
-
The 9 divisibility rule states that if the sum of the digits of a number is divisible by 9, then that number is divisible by 9.
-
If the last digit of a number is 0, then that number is divisible by 10.
-
A number is divisible by 11 if the difference between the sum of the digits at even places and the sum of the digits at odd places of a number is either 0 or divisible by 11.
Why are Class 8 Maths Chapter 5 Number Play Question Answers Important?
The Chapter Number Play in Class 8 helps students understand how numbers work together in different patterns. It shows simple tricks to check divisibility, find remainders, and work smartly with even and consecutive numbers. These Class 8 Maths Chapter 5 Number Play question answers make these concepts easy to practice and remember. Here are some more points on why these question answers are important:
- These solutions help you learn how to find patterns in numbers, like consecutive and even numbers.
- These question answers teach you quick ways to check divisibility and find remainders easily.
- These concepts are very useful later in higher classes when solving algebra and number system problems.
- Questions from this chapter often appear in school exams and Olympiads. So, checking these solutions will help students to improve their confidence and scoring ability.
NCERT Solutions for Class 8 Mathematics Chapter Wise
For students' preparation, Careers360 has gathered all Class 8 Maths NCERT solutions here for quick and convenient access.
NCERT Books and NCERT Syllabus
The following links will give students access to the latest NCERT syllabus and some reference books.
Frequently Asked Questions (FAQs)
When a number is divided by another, the leftover part is called the remainder.
Concepts like HCF, LCM, and prime factorisation are used in algebra, fractions, ratios, and problem-solving in higher classes. Practising them now makes these future topics much easier.
Yes, the sum of the first n natural numbers is given by the formula: [n(n-1)]/2
Yes, concepts like divisibility rules, prime factorisation, and number properties are very important and are used in higher classes and exams like Olympiads, NTSE, and entrance tests.
A digital root is the single-digit value obtained by continuously summing the digits of a number.
Example: Digital root of 121 is 1 + 2 + 1 = 4
It is useful to check divisibility, especially for 3 and 9.
If a number is divisible by 2 and 3, then that number is divisible by 6.
Because the LCM of 2 and 3 is 6.
The chapter focuses on topics such as number patterns, properties of numbers like divisibility rules, digital roots, prime factorisation, Remainders, cryptarithms, and classification of numbers.
Educational sites such as Careers360 provide detailed NCERT solutions for class 8 maths, including chapter 5, Number Play. These solutions are student-friendly and explained in a step-by-step manner.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
