NCERT Solutions for Class 8 Maths Chapter 7 - Proportional Reasoning-1

NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning-1: Download PDF

Careers360 brings you NCERT Class 8 Maths Chapter 7 Proportional Reasoning-1 solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.

Download PDF

NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning-1: Exercise Questions

Below are the detailed NCERT Class 8 Maths Chapter 7 Proportional Reasoning-1 question answers provided in the textbook.

Question 1. Circle the following statements of proportion that are true.
(i) $4: 7:: 12: 21$
(ii) $8: 3:: 24: 6$
(iii) $7: 12:: 12: 7$
(iv) $21: 6:: 35: 10$
(v) $12: 18:: 28: 12$
(vi) $24: 8:: 9: 3$

Answer:

A proportion means:
$a: b:: c: d$ is true if $\frac{a}{b}=\frac{c}{d}$

(1) $4: 7:: 12: 21$

$\frac{4}{7}=\frac{12}{21} \Rightarrow \frac{4}{7}=\frac{4}{7}$

This statement is True.

(ii) $8: 3:: 24: 6$

$\frac{8}{3}=\frac{24}{6} \Rightarrow \frac{8}{3}\neq4$

This statement is False.

(iii) $7: 12:: 12: 7$

$\frac{7}{12} \neq \frac{12}{7}$

This statement is False.

(iv) $21: 6:: 35: 10$

$\frac{21}{6}=\frac{7}{2} $ and $ \frac{35}{10}=\frac{7}{2}$

This statement is True.

(v) $12: 18:: 28: 12$

$\frac{12}{18}=\frac{2}{3}$ and $ \frac{28}{12}=\frac{7}{3} $

This statement is False.

(vi) $24: 8:: 9: 3$

$\frac{24}{8}=3 $ and $ \frac{9}{3}=3$

This statement is True.

Question 2. Give 3 ratios that are proportional to $4: 9$.
______ : ______  

______ : ______

______ : ______

Answer:

If we multiply both terms by the same number, we will get the same proportions.
Hence, the three ratios proportional to 4 : 9 are:

• $4 \times 2: 9 \times 2=8: 18$
• $4 \times 3: 9 \times 3=12: 27$
• $4 \times 5: 9 \times 5=20: 45$

Question 3. Fill in the missing numbers for these ratios that are proportional to 18:24.

3 : ______

12 : _______

20 : _______

27 : ________

Answer:

After simplifying, 18 : 24 becomes 3 : 4.
So for each given first term, we have to multiply by $\frac{4}{3}$ to get the second term.

3 : __[$3\times\frac43=4$]____ = 3 : 4

12 : ___[$12\times\frac43=16$]____ = 12 : 16

20 : ____[$20\times\frac43=\frac{80}{3}$]___= 20 : $\frac{80}3$

27 : ____[$27\times\frac43=36$]___ = 27 : 36

Question 4. Look at the following rectangles. Which rectangles are similar to each other? You can verify this by measuring the width and height using a scale and comparing their ratios.

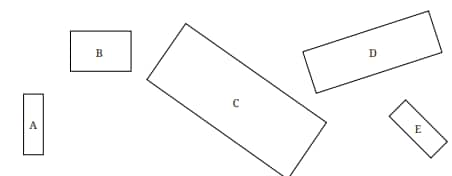
Answer:

Rectangles C, D, and E look similar.

Let the Length and Width of rectangle C be 3 and 9, respectively.

Let the Length and Width of rectangle D be 2 and 6, respectively.

Let the Length and Width of rectangle E be 1 and 3, respectively.
As we can see, all three ratios are equal and in the same proportion, 1 : 3.

Question 5. Look at the following rectangle. Can you draw a smaller rectangle and a bigger rectangle with the same width to height ratio in your notebooks?
Compare your rectangles with your classmates’ drawings. Are all of them the same? If they are different from yours, can you think why? Are they wrong?

Answer:

Smaller Rectangle:

Bigger Rectangle:

Question 6. The following figure shows a small portion of a long brick wall with patterns made using coloured bricks. Each wall continues this pattern throughout the wall. What is the ratio of grey bricks to coloured bricks? Try to give the ratios in their simplest form.

Answer:
(a)
Total bricks = 51
Red coloured bricks = 18
So, Grey coloured bricks = 51 - 18 = 33
$\therefore$ Required ratio = 33 : 18 = 11 : 6

(b)
Total bricks = 119
Yellow coloured bricks = 48
So, Grey coloured bricks = 119 - 48 = 71

$\therefore$ Required ratio = 71 : 48

Question 7. Let us draw some human figures. Measure your friend’s body—the lengths of their head, torso, arms, and legs. Write the ratios as mentioned below—

head : torso
______ : ______
torso : arms
______ : ______
torso : legs
______ : ______

Now, draw a figure with head, torso, arms, and legs with equivalent ratios as above.

Answer:

head : torso
= 1 : 1

torso : arms
= 1 : 2

torso : legs
= 1 : 2

Question 1. The Earth travels approximately 940 million kilometres around the Sun in a year. How many kilometres will it travel in a week?

Answer:

1 year = 52 weeks
940 million = 940,000,000 km

So, Earth travels approximately 940 million km in 52 weeks.
$\therefore$ In 1 week, it will travel $=\frac{940000000}{52}=18076923.08$ km or, 18.08 million km

Question 2. A mason is building a house in the shape shown in the diagram. He needs to construct both the outer walls and the inner wall that separates two rooms. To build a wall of 10-feet, he requires approximately 1450 bricks. How many bricks would he need to build the house? Assume all walls are of the same height and thickness.

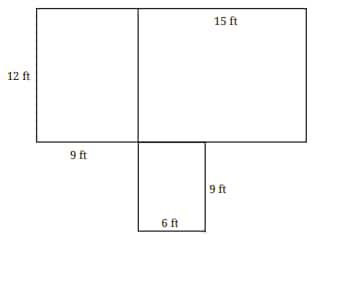
Answer:

Bigger rectangle length = 12 ft
Bigger rectangle width = 15 + 9 = 24 ft
Perimeter of bigger rectangle = 2(12 + 24) = 72 ft
Wall between the bigger rectangle = 12 ft

Smaller rectangle length = 9 ft
Smaller rectangle width = 6 ft
Perimeter of smaller rectangle = 2(9 + 6) = 30
But 6 ft of smaller rectangle has already been counted.
So, total wall length = 72 + 12 + 30 - 6 = 108 ft

To build a wall of 10-feet, he requires approximately 1450 bricks.
So, for a 108 ft wall, he needs $=\frac{1450}{10}\times108=15660$ bricks

Question 1. Divide ₹4,500 into two parts in the ratio 2 : 3.

Answer:

Total parts $=2+3=5$

Value of 1 part $=\frac{4500 } 5=900$

So, First part $=2 \times 900= 1800$

and Second part $=3 \times 900=2700$

Question 2. In a science lab, acid and water are mixed in the ratio of 1 : 5 to make a solution. In a bottle that has 240 mL of the solution, how much acid and water does the solution contain?

Answer:

Total parts $=1+5=6$

Value of 1 part $=\frac{240 }6=40 \mathrm{~mL}$

So, quantity of Acid $=1 \times 40=40 \mathrm{~mL}$

and quantity of Water $=5 \times 40=200 \mathrm{~mL}$

Question 3. Blue and yellow paints are mixed in the ratio of 3 : 5 to produce green paint. To produce 40 mL of green paint, how much of these two colours are needed? To make the paint a lighter shade of green, I added 20 mL of yellow to the mixture. What is the new ratio of blue and yellow in the paint?

Answer:

Blue and yellow paints are mixed in the ratio of 3 : 5 to produce green paint.
Total parts $=3+5=8$
Value of 1 part $=\frac{40 } 8=5 \mathrm{~mL}$
So, quantity of Blue $=3 \times 5=15 \mathrm{~mL}$
and quantity of Yellow $=5 \times 5=25 \mathrm{~mL}$

After adding 20 mL of Yellow:
Quantity of Blue remains unchanged, i.e., 15 mL
Quantity of Yellow becomes $=25+20=45 \mathrm{~mL}$

$\therefore$ New ratio of Blue and Yellow in the paint $=15: 45=1: 3$

Question 4. To make soft idlis, you need to mix rice and urad dal in the ratio of 2 : 1. If you need 6 cups of this mixture to make idlis tomorrow morning, how many cups of rice and urad dal will you need?

Answer:

To make soft idlis, you need to mix rice and urad dal in the ratio of 2 : 1.

Total parts $=2+1=3$

Value of 1 part $=\frac63=2$ cups

So, quantity of Rice $=2 \times 2=4$ cups

and quantity of Urad dal $=1 \times 2=2$ cups

Question 5. I have one bucket of orange paint that I made by mixing red and yellow paints in the ratio of 3 : 5. I added another bucket of yellow paint to this mixture. What is the ratio of red paint to yellow paint in the new mixture?

Answer:

I have one bucket of orange paint that I made by mixing red and yellow paints in the ratio of 3 : 5.

So, total parts = 3 + 5 = 8 parts

New quantity of red paint = 3 parts [Unchanged]
New quantity of yellow paint = 5 + 1 = 6 parts

$\therefore$ New ratio of red paint to yellow paint in the new mixture = 3 : 6 = 1 : 2

Question 1. Anagh mixes 600 mL of orange juice with 900 mL of apple juice to make a fruit drink. Write the ratio of orange juice to apple juice in its simplest form.

Answer:

Orange juice = 600 mL

Apple juice = 900 mL

$\therefore$ Required ratio = 600 : 900 = 2 : 3

Question 2. Last year, we hired 3 buses for the school trip. We had a total of 162 students and teachers who went on that trip, and all the buses were full. This year we have 204 students. How many buses will we need? Will all the buses be full?

Answer:

Last year, 162 students and teachers went on 3 buses, and the buses were full.
So, member per bus = $\frac{162}3=54$

For 204 members, we will need $54\times4 = 216$, i.e., 4 buses and the buses will not be full.

Question 3. The area of Delhi is 1,484 sq. km and the area of Mumbai is 550 sq. km. The population of Delhi is approximately 30 million, and that of Mumbai is 20 million people. Which city is more crowded? Why do you say so?

Answer:

Let's check the population density.

Delhi: $\frac{30,000,000}{1,484} \approx 20,215$ people/sq.km

Mumbai: $\frac{20,000,000}{550} \approx 36,364$ people/sq.km

Mumbai has a higher density of people.

So, Mumbai is more crowded.

Question 4. A crane of height 155 cm has its neck and the rest of its body in the ratio 4 : 6. For your height, if your neck and the rest of the body also had this ratio, how tall would your neck be?

Answer:

$ \text { Total height }=155 \mathrm{~cm}$

$ \text { Neck }: \text { rest of body }=4: 6$

So, there are total 4 + 6 = 10 parts

$\therefore \text { Neck height }=\frac{4}{10} \times 155=62 \mathrm{~cm}$

Question 5. Let us try an ancient problem from Lilavati. At that time, weights were measured in a unit named palas, and niskas was a unit of money. "If $2 \frac{1}{2}$ palas of saffron costs $\frac{3}{7}$ niskas, O expert businessman! Tell me quickly what quantity of saffron can be bought for 9 niskas?"

Answer:

$2\frac12$ palas $=\frac52$ palas cost $\frac{3}{7}$ niskas

$\therefore$ Cost per pala $=\frac{\frac{3}{7}}{\frac52}=\frac{3}{7} \times \frac{2}{5}=\frac{3}{7} \times \frac{2}{5}=\frac{6}{35}$ niskas/pala

So, for 9 niskas, the quantity of palas needed:

$=\frac{9}{\frac{5}{35}}=9 \times \frac{35}{6}=\frac{315}{6}=52.5$ palas

Question 6. Harmain is a 1-year-old girl. Her elder brother is 5 years old. What will be Harmain's age when the ratio of her age to her brother's age is $1: 2$?

Answer:
Let Harman's age be x, and her brother's age is 2x when their age ratio is 1:2.
According to the question,
2x = x + 4 [As Harman is 4 years younger than her brother]
$\Rightarrow x=4$

Hence, Harman’s age will be 4 years when the ratio of her age to her brother's age is $1: 2$.

Question 7. The mass of equal volumes of gold and water are in the ratio $37: 2$. If 1 litre of water is 1 kg in mass, what is the mass of 1 litre of gold?

Answer:

The mass of equal volumes of gold and water is in the ratio $37: 2$
That means if the same volume of gold weighs 37 units, the same volume of water weighs 2 units.

We know 1 litre of water has a mass of 1 kg.
In the ratio, Water’s “2 parts” corresponds to 1 kg.
So, 1 part = $\frac12=0.5$ kg
From the ratio 37 : 2, gold’s mass is 37 parts.
So, 1 litre of gold weighs $=37\times0.5=18.5$ kg

Question 8. It is good farming practice to apply 10 tonnes of cow manure for 1 acre of land. A farmer is planning to grow tomatoes in a plot of size 200 ft by 500 ft. How much manure should he buy? (Please refer to the section on Unit Conversions earlier in this chapter).

Answer:

We know, 1 acre = 43560 sq ft
So, 10 tonnes of cow manure is used for 43500 sq ft

Land size: $200 \times 500=100,000$ sq ft.

Area in acres $=\frac{100,000}{43,560} \approx 2.29$ acres

$\therefore$ Manure needed $=10$ tonnes $\times 2.29 \approx 22.9$ tonnes

Question 9. A tap takes 15 seconds to fill a mug of water. The volume of the mug is 500 mL. How much time does the same tap take to fill a bucket of water if the bucket has a 10-litre capacity?

Answer:

10 litre = 10000 mL

A tap takes 15 seconds to fill 500 mL

Ratio of volumes $=10000: 500=20: 1$

So, it fills 1 part in 15 seconds.

$\therefore$ The same tap will fill 10-litre capacity bucket in:

$=15 \times 20=300$ seconds $=5$ minutes

Question 10. One acre of land costs ₹15,00,000. What is the cost of 2,400 square feet of the same land?

Answer:

We know, 1 acre = 43560 sq ft

One acre of land costs ₹15,00,000, i.e, 43560 sq ft of land costs ₹15,00,000

$\therefore$ 2,400 square feet of land costs = $\frac{1500000}{43560}\times2400\approx$ ₹$ 82645$

Question 11. A tractor can plough the same area of a field 4 times faster than a pair of oxen. A farmer wants to plough his 20-acre field. A pair of oxen takes 6 hours to plough an acre of land. How much time would it take if the farmer used a pair of oxen to plough the field? How much time would it take him if he decides to use a tractor instead?

Answer:

Given: If a pair of oxen takes 4 hours to plough the same area of a field, then a tractor will take 1 hour, as A tractor can plough the same area of a field 4 times faster than a pair of oxen.

A pair of oxen takes 6 hours to plough an acre of land.
For 20 acres, a pair of oxen will take = $6\times20=120$ hours
$\therefore$ A tractor will take $=\frac{120}4=30$ hours

Question 12. The ₹10 coin is an alloy of copper and nickel called ‘cupro-nickel’. Copper and nickel are mixed in a 3 : 1 ratio to get this alloy. The mass of the coin is 7.74 grams. If the cost of copper is ₹906 per kg and the cost of nickel is ₹1,341 per kg, what is the cost of these metals in a ₹10 coin?

Answer:

Copper and nickel are mixed in a 3 : 1 ratio to get this alloy.

Mass of copper $=\frac{3}{3+1} \times 7.74=5.805 \mathrm{~g}=0.005805 \mathrm{~kg}$

Mass of nickel $=\frac{1}{3+1} \times 7.74=1.935 \mathrm{~g}=0.001935 \mathrm{~kg}$

Cost of copper $=0.005805 \times 906 \approx$ ₹5.26

Cost of nickel $=0.001935 \times 1341 \approx$ ₹ 2.59

NCERT Proportional Reasoning-1 Class 8 Chapter 7: Topics

Students will explore the following topics in NCERT Class 8 Maths Chapter 7 Proportional Reasoning-1:

• Observing Similarity in Change
• Ratios
• Ratios in Their Simplest Form
• Problem Solving with Proportional Reasoning
• Trairasika—The Rule of Three
• Sharing, but Not Equally!
• Unit Conversions

Class 8 Maths Chapter 7 Proportional Reasoning-1 Solutions: Extra Question

Question:

The sum of the present ages of a father and his son is 94 years. 8 years ago, their respective ages were in the ratio of 2 : 1. After 10 years, what will be the ratio of ages of father and son?

Solution:

Let the present age of the father be $x$ and the present age of the son be $y$.
Given: $x + y = 94$.................(1)
8 yrs ago,
$\frac{x-8}{y-8}=\frac{2}{1}$
⇒ $x-8=2y-16$
⇒ $x-2y=-8$................(2)
Subtracting equation (2) from equation (1), we get:
$3y=102$
⇒ $y=34$
⇒ $x = 94-34=60$
$\therefore$ Son = 34 years and Father = 60 years
After 10 years,
The ratio of father and son ages = (60 + 10) : (34 + 10) = 70 : 44 = 35 : 22
Hence, the correct answer is 35 : 22.

NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning-1: Notes

Careers360 has prepared these Class 8 Proportional Reasoning-1 Notes to make your revision smoother and faster. Additionally, these notes will help you understand this chapter better and deal with the Proportional Reasoning-1 NCERT questions with ease.

Ratio

To compare two quantities or check how many times one quantity is contained in another quantity, we use a Ratio.

A and B are said to be in ratio if it is written A : B or $\frac{A}{B}$, Where B $\neq 0$

It is read as “A is to B”.

The left side of the ratio is called the Antecedent, and the right side is called the Consequent.

Ratio is denoted by “:”.

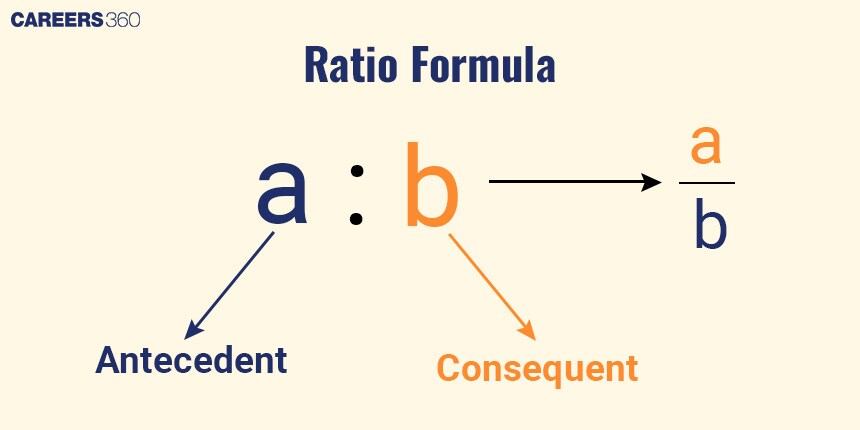
Example: Boy : Girl = 1 : 3, which means for every 1 boy, there are 3 girls.

Proportion

Two ratios a : b and x : y are said to be proportional to each other if a : b = x : y

It is written as a : b :: x : y.

a and y are called “extreme terms” and b and x are called “mean terms”.

Proportion is denoted by “::”.

Comparing two or more ratios

Comparing two or more ratios can be done through various methods like cross multiplication, converting to decimal form or finding a common numerator or denominator.

First, convert the ratios into fractions, then calculate.

$a : b > c : d$, if $\frac{a}{b}$ > $\frac{c}{d}$

Types of Ratios

There are various types of ratios, each with its own characteristics and applications.

Here are some main types of ratios listed below.

1. Simple ratio

2. Inverse ratio

3. Continued ratio

4. Equivalent ratio

5. Duplicate ratio

6. Triplicate ratio

7. Sub duplicate ratio

8. Sub triplicate ratio

9. Compounded ratio

Problems on ages

We can use ratios to solve problems involving age. Suppose the ratio of ages and the total age are given. First, we express the ratio terms using a variable. Then, we calculate the value of the variable using an algebraic method.

For example, if the age ratio of a father and son is 4 : 1, we can express their ages using the variable x. The father's age would be 4x, and the son's age would be x.

Unit Conversions

Unit conversion means changing a measurement from one unit to another, without changing the actual amount.
It helps us compare or calculate things in the same unit.

Here are some useful unit conversions for length.

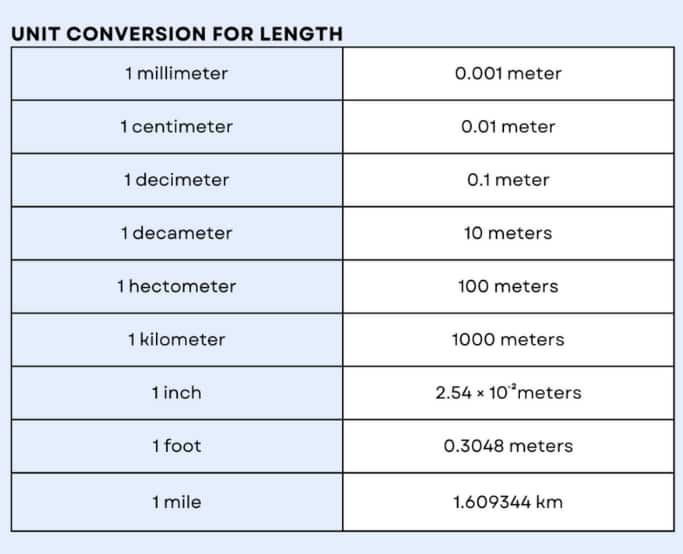
NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning-1: Important Formulae

These formulas will help you understand this chapter better and deal with the Proportional Reasoning-1 NCERT questions with ease.

NCERT Solutions for Class 8 Mathematics - Chapter Wise

We at Careers360 compiled all the NCERT class 8 Maths solutions in one place for easy student reference. The following links will allow you to access them.

NCERT Books and NCERT Syllabus

The following links will take students to the latest NCERT syllabus and some reference books.

• NCERT Books Class 8 Maths
• NCERT Syllabus Class 8 Maths
• NCERT Books Class 8
• NCERT Syllabus Class 8