NCERT Solutions for Class 8 Maths Chapter 3 - A Story of Numbers
Before calculators and computers, ancient people had various clever ways to count, which we will explore in Class 8 Maths NCERT Chapter 3 A Story of Numbers. Behind every modern number lies an ancient symbol, an idea, or a culture. The chapter A Story of Numbers will teach us how numbers were created, used, and improved across different ancient civilisations. From the Egyptian to the Mayan, and from the Chinese to our very own Hindu number system, these topics have been explored in this chapter. The primary objective of these solutions is to help us understand how counting originated and how it has evolved across various civilisations. NCERT Solutions for Class 8 focus on improving problem-solving skills and revising each chapter effectively.
This Story also Contains
- NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers: Download Free PDF
- NCERT Solutions for Class 8 Maths Chapter 3: Exercise Questions
- A Story of Numbers Class 8 Chapter 3: Topics
- NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers: Notes
- NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers: Points to remember
- Why are Class 8 Maths Chapter 3 A Story of Numbers Question Answers Important?
- NCERT Solutions for Class 8 Mathematics - Chapter Wise
- NCERT Books and NCERT Syllabus

With these NCERT solutions for Class 8 Maths, students will learn about the rich history and gain a deeper understanding of the origins of the number system used in modern mathematics. These solutions are prepared by experienced Careers360 teachers in accordance with the latest syllabus. Students prefer NCERT Solutions as they make revision easier and more effective. This article provides comprehensive, step-by-step solutions to the chapter's questions in a student-friendly format. For full syllabus coverage and solved exercises as well as a downloadable PDF, please visit this NCERT article.
NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers: Download Free PDF
Careers360 brings you NCERT Class 8 Maths Chapter 3 A Story of Numbers solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 8 Maths Chapter 3: Exercise Questions
NCERT Class 8 Maths Chapter 3 A Story of Numbers question answers with detailed explanations are provided below.
|
A Story of Numbers Class 8 Question Answers |
Question 1. Suppose you are using the number system that uses sticks to represent numbers, as in Method 1. Without using either the number names or the numerals of the Hindu number system, give a method for adding, subtracting, multiplying and dividing two numbers or two collections of sticks.
Answer:
Adding:
In addition, we can merge the two collections of sticks and count.
Subtracting:
In subtraction, after counting the total sticks in two collections, we can remove a number of sticks from the collection and recount the sticks.
Multiplying:
Multiplication is repeated addition. So you can combine all the sticks and then count them one by one, row-wise or column-wise.
Dividing:
In division, you can split the bundle of sticks into equal-sized groups. The total number of sticks is the dividend, the number of sticks in a group is the divisor, and the number of groups is the quotient.
If sticks remain outside the groups, those are the remainder.
Question 2. One way of extending the number system in Method 2 is by using strings with more than one letter—for example, we could use ‘aa’ for 27. How can you extend this system to represent all the numbers? There are many ways of doing it!
Answer:
If aa is 27, then we can extend this system for the next 27 digits, like the following table.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Other ways:
We can use lower-case letters for 1 to 26 and upper-case letters for 27 to 52 and make a number system.
Question 3. Try making your own number system.
Answer:
My number system will be represented as follows.
Zero: □
One: .
Two: :
Three: :.
Four: ::
Five: ::.
Six: :::
Seven: :::.
Eight: ::::
Nine: ::::.
Ten: :::::
|
A Story of Numbers Class 8 Question Answers |
Question 1. Represent the following numbers in the Roman system.
(i) 1222 (ii) 2999 (iii) 302 (iv) 715
Answer:
(i) 1222
- 1000 = M
- 200 = CC
- 20 = XX
- 2 = II
Answer: MCCXXII
(ii) 2999
- 2000 = MM
- 900 = CM
- 90 = XC
- 9 = IX
Answer: MMCMXCIX
(iii) 302
- 300 = CCC
- 2 = II
Answer: CCCII
(iv) 715
- 500 = D
- 200 = CC
- 10 = X
- 5 = V
Answer: DCCXV
| A Story of Numbers Class 8 Question Answers Figure it Out Page number: 60-61 |
Question 1. A group of indigenous people in a Pacific island use different sequences of number names to count different objects. Why do you think they do this?
Answer:
Different objects may have different importance or characteristics, so counting them separately helps avoid confusion.
For example, they could have used one sequence to count the number of people, one sequence to count fruits or flowers, one sequence to count fish, and so on.
Question 2. Consider the extension of the Gumulgal number system beyond 6 in the same way of counting by 2s. Come up with ways of performing the different arithmetic operations (+, –, ×, ÷) for numbers occurring in this system, without using Hindu numerals. Use this to evaluate the following:
(i) (ukasar-ukasar-ukasar-ukasar-urapon) + (ukasar-ukasarukasar-urapon)
(ii) (ukasar-ukasar-ukasar-ukasar-urapon) – (ukasar-ukasarukasar)
(iii) (ukasar-ukasar-ukasar-ukasar-urapon) × (ukasar-ukasar)
(iv) (ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar) ÷ (ukasar-ukasar)
Answer:
Let “ukasar” be 2 and “urapon” be 1.
(i)
First number: 4 ukasars + 1 urapon = (4 × 2) + 1 = 8 + 1 = 9
Second number: 3 ukasars + 1 urapon = 6 + 1 = 7
Total Sum = 9 + 7 = 16
In the Gumulgal number system, we can write 16 as 8 times ukasar.
[ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar]
(ii)
First: 4 ukasars + 1 urapon = 9
Second: 3 ukasars = 6
Difference = 9 – 6 = 3
In the Gumulgal number system, we can write 3 as 1 ukasar and 1 urapon:
[ukasar-urapon]
(iii)
First: 4 ukasars + 1 urapon = 9
Second: 2 ukasars = 4
Multiplication: 9 × 4 = 36
In the Gumulgal number system, we can write 36 as 18 times ukasar.
[ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar]
(iv)
Dividend: 8 ukasars = 16
Divisor: 2 ukasars = 4
Division: 16 ÷ 4 = 4
In the Gumulgal number system, we can write 4 as 2 times ukasar.
[ukasar-ukasar]
Question 3. Identify the features of the Hindu number system that make it efficient when compared to the Roman number system.
Answer:
Here are features of the Hindu Number System that make it more efficient than the Roman number system.
Use of zero: Hindu number systems use zero as a number and place holder that makes calculations and notations easier.
Place value: In the Hindu number system, each digit has a separate value, such as tens, hundreds, etc. It helps count larger numbers easily.
Arithmetic operations: Addition, subtraction, multiplication, and division are easier due to the place values of the Hindu number system.
Unique representation: Larger numbers are presented with fewer symbols in the Hindi number system, which makes the number more readable and writable.
Question 4. Using the ideas discussed in this section, try refining the number system you might have made earlier.
Answer:
We can use the following rules to refine the earlier system.
- Introducing a place value system to represent units and multiples to base to represent bigger numbers efficiently.
- Adding zero as a placeholder and a number.
- Inventing distinct symbols to avoid confusion and to make the representation clearer.
- Ensuring the numbers can be used for smooth arithmetic operations such as addition, subtraction, multiplication, and division.
| A Story of Numbers Class 8 Question Answers Figure it Out Page number: 61 |
Question 1. Represent the following numbers in the Egyptian system:
10458, 1023, 2660, 784, 1111, 70707.
Answer:
10458:

1023:
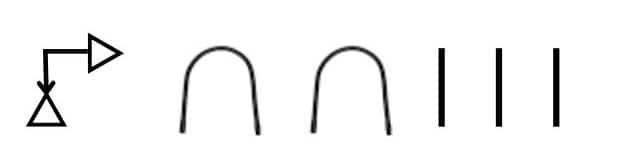
2660:

784:

1111:
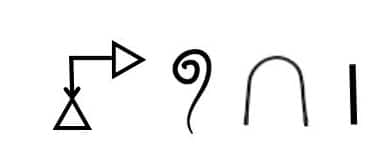
70707:
Question 2. What numbers do these numerals stand for?
.jpg)
Answer:
(i)
100 + 100 + 10 + 10 + 10 + 10 + 10 + 10 + 3 + 3 + 10 = 276
(ii)
1000 + 1000 + 1000 + 1000 + 100 + 100 + 100 + 2 + 10 + 10 = 4322
| A Story of Numbers Class 8 Question Answers Figure it Out Page number: 63 |
Question 1. Write the following numbers in the above base-5 system using the symbols in Table 2:
15, 50, 137, 293, 651.
Answer:
15: $5^1+5^1+5^1$
50: $5^2+5^2$
137: $5^3+5^1+5^1+5^0+5^0$
293: $5^3+5^3+5^2+5^1+5^1+5^1+5^0+5^0+5^0$

651: $5^4+5^2+5^0$
Question 2. Is there a number that cannot be represented in our base-5 system above? Why or why not?
Answer:
No, every whole number (non-negative integer) can be represented in the base-5 system.
This is because base-5 is a positional number system that uses powers of 5 and digits 0 through 4 to represent any number uniquely. Any integer can be broken down as a sum of multiples of powers of 5, so the system is complete for all integers.
Question 3. Compute the landmark numbers of a base-7 system. In general, what are the landmark numbers of a base-$n$ system?
The landmark numbers of a base- $n$ number system are the powers of $n$ starting from $n^0=1, n, n^2, n^3, \ldots$
Answer:
For base-7, the landmark numbers are:
- $7^0=1$
- $7^1=7$
- $7^2=49$
- $7^3=343$
- $7^4=2401$, and so on.
| A Story of Numbers Class 8 Question Answers Figure it Out Page number: 65 |
Question 1. Add the following Egyptian numerals:
.jpg)
Answer:
(i)
1000 + 1000 + 1000 + 100 + 100 + 100 + 100 + 100 + 100 + 8 = 3608
And
100 + 100 + 100 + 100 + 100 + 7 = 507
Sum = 3608 + 507 = 4115
(ii)
1000 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 1080
And
10 + 10 + 10 + 10 + 10 + 6 = 56
Sum = 1080 + 56 = 1136
Question 2. Add the following numerals that are in the base-5 system that we created:
Remember that in this system, 5 times a landmark number gives the next one!
Answer:
$5^3+5^2+5^2+5^1+5^0+5^0$ = 182
And
$5^3 + 5^3 + 5^3 + 5^2 + 5^1+5^1+5^0+5^0$ = 412
Sum = 182 + 412 = 594
| A Story of Numbers Class 8 Question Answers Figure it Out Page number: 69-70 |
Question 1. Can there be a number whose representation in Egyptian numerals has one of the symbols occurring 10 or more times? Why not?
Answer:
No, there can not be a number whose representation in Egyptian numerals has one of the symbols occurring 10 or more times.
Suppose we use the Egyptian symbol 1, 10 times, we will get 10, but there is already a separate symbol for 10, which we can use just once to represent 10.
Question 2. Create your own number system of base 4, and represent numbers from 1 to 16.
Answer:
For base-4, the landmark numbers are:
$4^0=1, 4^1=4,4^2=16,4^3=64,4^4=256$ and so on
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 3. Give a simple rule to multiply a given number by 5 in the base-5 system that we created.
Answer:
To multiply a number by 5 in base-5, simply add a 0 at the right end of its base-5 representation. Also, increase the power by 1 to equal it.
Example:
$50=5^2+5^2$
Now, if we multiply 50 by 5, we get 250.
250: $5^3+5^3$
We have just increased the powers by 1.
| A Story of Numbers Class 8 Question Answers Figure it Out Page number: 73 |
Question 1. Represent the following numbers in the Mesopotamian system —
(i) 63 (ii) 132 (iii) 200 (iv) 60 (v) 3605
Answer:
63: 1 × 60 + 3

132: 2 × 60 + 2
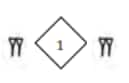
200: 3 × 60 + 2 × 10

60: 1 × 60

3605: $60^2$ + 5
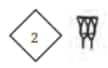
| A Story of Numbers Class 8 Question Answers Figure it Out Page number: 80 |
Question 1. Why do you think the Chinese alternated between the Zong and Heng symbols? If only the Zong symbols were to be used, how would 41 be represented? Could this numeral be interpreted in any other way if there is no significant space between two successive positions?
Answer:
The Chinese alternated between Zong (vertical) and Heng (horizontal) symbols to make numbers easier to read and less confusing. Alternating symbols helped distinguish between different place values at a glance.
The Zong symbols represent units, hundreds, tens of thousands, and so on, while the Heng symbols stand for tens, thousands, hundreds of thousands, and beyond.
41 in zong symbols:
4 × 10 + 1
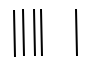
Without a clear space between positions, it could be misread as 5 tens or 45 units, because it would be unclear where one place ends and the next begins. This shows why alternating symbols or spacing is important in positional notation.
Question 2. Form a base-2 place value system using ‘ukasar’ and ‘urapon’ as the digits. Compare this system with that of the Gumulgal’s.
Answer:
Lets suppose "urapon" = 0 and "ukasar" = 1
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In the Gumulgal system, numbers are counted in pairs, but use word sequences for quantities rather than place value.
For example, “ukasar-ukasar-urapon” could represent 5
This base-2 number system with ukasar/urapon uses place value for each position to the left, which is worth double the one before. The meaning of a digit depends on where it is placed, making the system much more compact for large numbers.
Question 3. Where in your daily lives, and in which professions, do the Hindu numerals, and 0, play an important role? How might our lives have been different if our number system and 0 hadn’t been invented or conceived of?
Answer:
In our daily lives, Zero is used in Money calculations, clocks, calendars, phone numbers, computer use, and shopping bills.
Zero is used in professions like Accountants, engineers, scientists, programmers, teachers, statisticians, and bankers.
The importance of Zero in the number system is significant. It acts as a placeholder.
Without zero:
- Calculations would be slow and confusing.
- Large numbers will be hard to write and deduce.
- Modern computers, engineering, and scientific calculations may not have been possible.
Question 4. The ancient Indians likely used base 10 for the Hindu number system because humans have 10 fingers, and so we can use our fingers to count. But what if we had only 8 fingers? How would we be writing numbers then? What would the Hindu numerals look like if we were using base 8 instead? Base 5? Try writing the base-10 Hindu numeral 25 as base-8 and base-5 Hindu numerals, respectively. Can you write it in base-2?
Answer:
Base 8 representation:
$8^0=1,8^1=8,8^2=64,8^3=512,8^4=4096,$ and so on.
Base 5 representation:
$5^0=1,5^1=5,5^2=25, 5^3=125,5^4=625,$ and so on.
Summary table of 25:
|
|
|
|
|
|
|
|
|
|
|
|
If humans had 8 fingers, a base-8 number system might have been natural, just like base-10 is natural for 10 fingers. Similarly, base-5 could come from 5 fingers per hand.
A Story of Numbers Class 8 Chapter 3: Topics
Here are the key topics covered in the NCERT Solutions for Class 8 Chapter 3 A Story of Numbers:
- Introduction
- The Mechanism of Counting
- Some Early Number Systems
- The Egyptian Number System
- Variations on the Egyptian System and the Notion of Base
- Shortcomings of the Egyptian System
- The Mesopotamian Number System
- The Mayan Number System
- The Chinese Number System
- The Hindu Number System
NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers: Notes
Careers360 has prepared these Class 8 A Story of Numbers Notes to make your revision smoother and faster. Additionally, these notes will help students understand the A Story of Numbers Class 8 solutions and solve them on their own from next time.
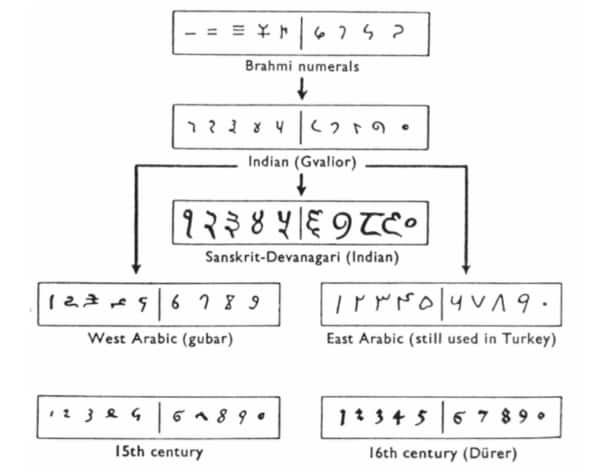
The Indian number system has evolved over the years. The picture below shows the transformation of numbers over a period.
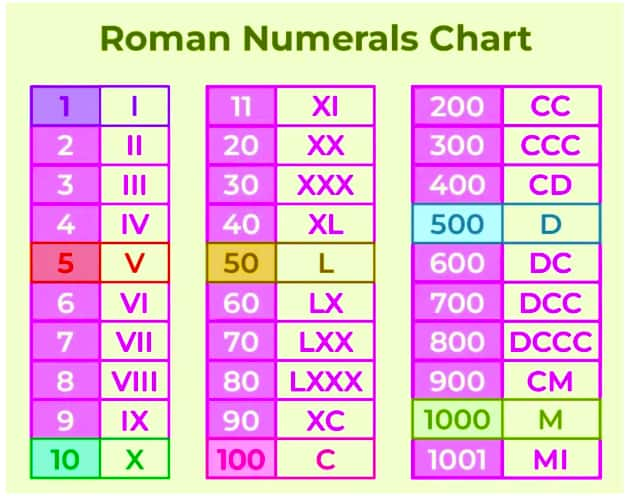
The Roman Numerals
The Roman numeral system is one of the most famous early number systems developed by the ancient Romans. Roman numerals are still an integral part of the number system today. Here is a chart of Roman numerals.
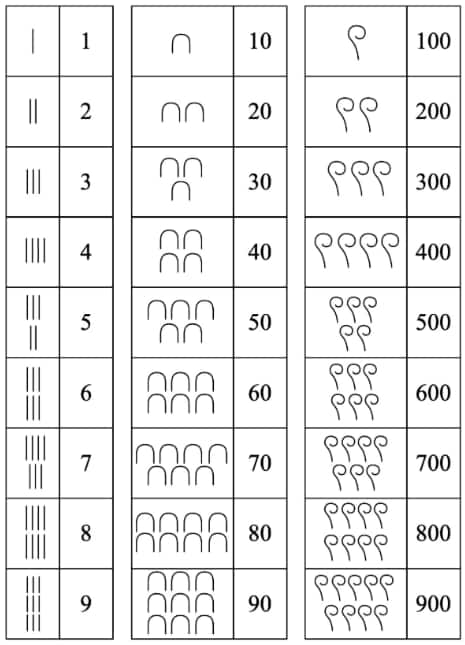
Egyptian Number System
The Egyptian number system is one of the oldest forms of number. In this system, numbers were additive; symbols were repeated to add up values. There is also no concept of zero.
Here are the symbols of the Egyptian number system
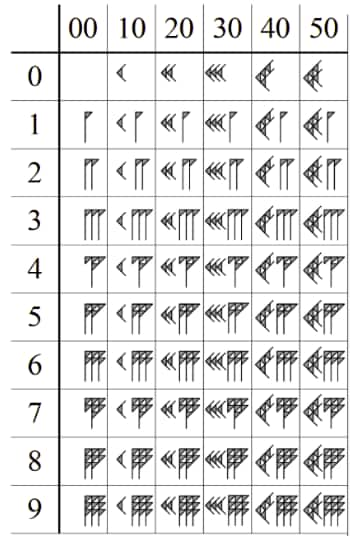
The Mesopotamian Number System
The Mesopotamian number system came after the Egyptian number system, but it is still a much older number system than other number systems. It is the first number system that used positional values similar to our modern system, but base 60. Initially, there was no concept of zero; later, a placeholder symbol was added. The basis of 60 minutes in an hour and 360° in a circle today comes from this number system.
Here is a look at the Mesopotamian number system.
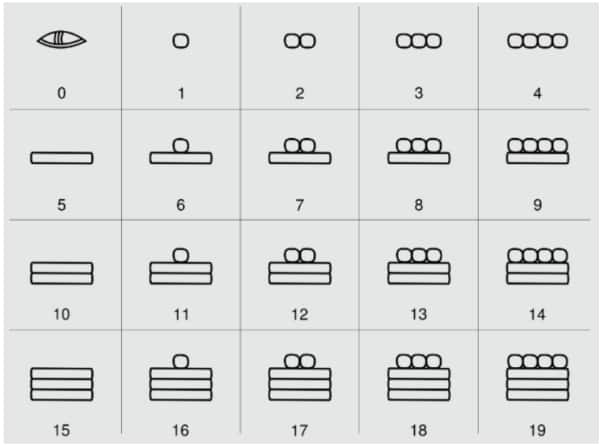
The Mayan Number System
The Mayan number system came forward around 300 BCE. (Before Common Era) In this number system, the place value system is used vertically (bottom to top). It is also widely used in astronomy and calendars. Here is a look at the Mayan number system.
The Chinese Number System
The Chinese number system used vertical and horizontal rods to represent digits 1–9. At later stages, they used blank spaces to represent zero.
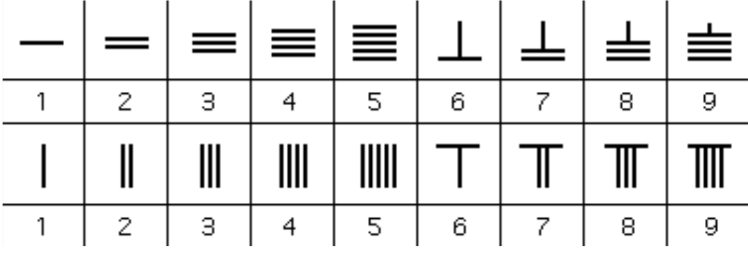
The Hindu Number System
The Hindu number system, or as we call it, the Hindu-Arabic number system, revolutionised mathematics by inventing zero as a numeral. The values in this system are fully positional, making arithmetic simple. The system originated in India around 2000 years ago, and then spread across the world, and is considered one of human history’s greatest inventions.
Here is a look at the Hindu-Arabic number system.
.jpg)
NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers: Points to remember
Here are important points that will help students find the Class 8 Maths Chapter 3 solutions.
- A number system is a systematic way to write, represent, and perform calculations with numbers using digits and a base.
- The symbols representing numbers in a written number system are called numerals.
- Early humans used tally marks (sticks, bones, stones) to count objects.
- Study the Roman symbols carefully. Some common Roman symbols are I, V, X, L, C, D, and M.
These stand for 1, 5, 10, 50, 100, 500, and 1000, respectively. - The Mesopotamian number system influenced modern time (60 minutes) and angles (360°).
- Place value representations were used in the Mesopotamian (Babylonian), Mayan, Chinese and Indian civilisations.
- The Mayan number system was one of the earliest systems to use zero as a symbol.
- The concept of zero as a number and a placeholder originated in India. Indian mathematicians Aryabhata and Brahmagupta contributed significantly to the concept of zero and place value.
Why are Class 8 Maths Chapter 3 A Story of Numbers Question Answers Important?
The 3rd Chapter of class 8, A Story of Numbers, helps students learn how counting and number systems began and changed over time. It explains how different civilisations like the Egyptians, Mayans, and Hindus used numbers in their own ways. These Class 8 Maths Chapter 3 A Story of Numbers question answers help you understand these concepts simply and interestingly. Here are some more points of why these question answers are important.
- These solutions help students understand how counting and number systems developed in different parts of the world.
- These questions make it easy to compare old number systems and understand their uses.
- The knowledge learned from this chapter helps students in higher classes when learning about place value and number bases.
- Practising Class 8 Maths A Story of Numbers question answers improves your understanding of how modern maths grew from ancient systems.
NCERT Solutions for Class 8 Mathematics - Chapter Wise
We at Careers360 compiled all the NCERT class 8 Maths solutions in one place for easy student reference. The following links will allow you to access them.
|
NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube |
|
NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers |
|
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply |
|
NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning-1 |
NCERT Books and NCERT Syllabus
Understanding the latest syllabus is a crucial step in achieving good marks in the exam. Students can use the following links to find the syllabus and some reference books.
Frequently Asked Questions (FAQs)
The Mesopotamian system (developed by the Sumerians and Babylonians) used base 60 and had a positional value system, making it more advanced. Traces of base 60 remain today in time (60 seconds) and angles (360°).
The Chinese used rod numerals and a decimal (base 10) system. They also used counting boards for calculations, similar in concept to the abacus.
The Egyptian system used picture symbols for numbers. It was additive (symbols were added together to form numbers) and used base 10, but without a symbol for zero.
Students can get the NCERT solutions for free from various trusted educational websites such as Careers360. At Careers360, these solutions are created by experienced subject matter experts to provide clear, step-by-step answers to all exercises in the chapter, making it easier to understand concepts and solve questions accurately.
This chapter explores the history and development of number systems, including ancient methods of counting, different numeral systems, and the evolution of the modern Hindu–Arabic numeral system.
Also, various other number systems are discussed in this chapter, such as:
The Egyptian Number System
The Mesopotamian Number System
The Mayan Number System
The Chinese Number System
The Hindu Number System
Yes, for exams based on the NCERT syllabus, these solutions are more than enough. These solutions will also build a strong foundation for solving similar questions. Students can also practice extra questions from other resources to boost their confidence.
This alternation between Zong and Heng symbols helped avoid confusion between adjacent digits and made reading numbers easier.
The Zong symbols represent units, hundreds, tens of thousands, and so on, while the Heng symbols stand for tens, thousands, hundreds of thousands, and beyond.
The Hindu number system introduced the concept of zero and place value, which transformed mathematics and made calculations faster and easier.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
