NCERT Solutions for Class 8 Maths Chapter 2 - Power Play

NCERT Solutions for Class 8 Maths Chapter 2 Power Play: Download PDF

Careers360 brings you NCERT Class 8 Maths Chapter 2 Power Play solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF has been provided — click on the link below to access it.

Download PDF

NCERT Solutions for Class 8 Maths Chapter 2 Power Play: Exercise Questions

Below are the detailed NCERT Class 8 Maths Chapter 2 Power Play question answers provided in the textbook.

Question 1. Express the following in exponential form:
(i) $6 \times 6 \times 6 \times 6$
(ii) $y \times y$
(iii) $b \times b \times b \times b$
(iv) $5 \times 5 \times 7 \times 7 \times 7$
(v) $2 \times 2 \times a \times a$
(vi) $a \times a \times a \times c \times c \times c \times c \times d$

Answer:

(i) $6 \times 6 \times 6 \times =6^4$

(ii) $y \times y=y^2$

(iii) $b \times b \times b \times b=b^4$

(iv) $5 \times 5 \times 7 \times 7 \times 7=5^2 \times 7^3$

(v) $2 \times 2 \times a \times a=2^2 \times a^2$

(vi) $a \times a \times a \times c \times c \times c \times c \times d=a^3 \times c^4 \times d$

Question 2. Express each of the following as a product of powers of their prime factors in exponential form.
(i) 648
(ii) 405
(iii) 540
(iv) 3600

Answer:

(i) $648 = 2^3 \times 3^4$

(ii) $405 = 3^4 \times 5$

(iii) $540 = 2^2 \times 3^3 \times 5$

(iv) $3600 = 2^4 \times 3^2 \times 5^2$

Question 3. Write the numerical value of each of the following:
(i) $2 \times 10^3$
(ii) $7^2 \times 2^3$
(iii) $3 \times 4^4$
(iv) $(-3)^2 \times(-5)^2$
(v) $3^2 \times 10^4$
(vi) $(-2)^5 \times(-10)^6$

Answer:

(i) $2 \times 10^3=2 \times 1000 = 2000$

(ii) $7^2 \times 2^3=49 \times 8 = 392$

(iii) $3 \times 4^4=3 \times 256 = 768$

(iv) $(-3)^2 \times (-5)^2=9 \times 25 =225$

(v) $3^2 \times 10^4=9 \times 10000 = 90000$

(vi) $(-2)^5 \times (-10)^6=(-32) \times 1000000 = -32000000$

Question 1. Find out the units digit in the value of $2^{224} \div 4^{32}$?
[Hint: $4=2^2$ ]

Answer:

$4^{32} = (2^2)^{32} = 2^{64}$
So, $\dfrac{2^{224}}{2^{64}} = 2^{160}$

We know the unit digit of powers of 2 follows a cycle of 4 :
$2^1=2 \rightarrow$ unit digit $=2$
$2^2=4 \rightarrow$ unit digit $=4$
$2^3=8 \rightarrow$ unit digit $=8$
$2^4=16 \rightarrow$ unit digit $=6$
Then it repeats: $2,4,8,6, \ldots$
So, we have to divide the exponent by $4: 160 \div 4=40$
If divisible exactly, the 4th number in the cycle is the unit digit, i.e., 6.

Question 2. There are 5 bottles in a container. Every day, a new container is brought in. How many bottles would be there after 40 days?

Answer:

Every day, a new container is brought in.
I.e., Each day = 5 bottles
So, after 40 days, there will be 40 days × 5 = 200 bottles

Question 3. Write the given number as the product of two or more powers in three different ways. The powers can be any integers.
(i) $64^3$
(ii) $192^8$
(iii) $32^{-5}$

Answer:

(i) $64^3$

• $64 = 2^6$ → $(2^6)^3 = 2^{18}$
• $64 = 4^3$ → $(4^3)^3 = 4^9$
• $64 = 8^2$ → $(8^2)^3 = 8^6$

(ii) $192^8$

• $192 = 2^6 \times 3$ → $(2^6 \times 3)^8 = 2^{48} \times 3^8$
• $192 = 64 \times 3$ → $(64 \times 3)^8 = 64^8 \times 3^8$
• $192 = 2^3 \times 24$ → $(2^3 \times 24)^8 = 2^{24} \times 24^8$

(iii) $32^{-5}$

• $32 = 2^5$ → $(2^5)^{-5} = 2^{-25}$
• $32 = 4 \times 8$ → $(4 \times 8)^{-5} = 4^{-5} \times 8^{-5}$
• $32 = 16 \times 2$ → $(16 \times 2)^{-5} = 16^{-5} \times 2^{-5}$

Question 4. Examine each statement below and find out if it is 'Always True', 'Only Sometimes True', or 'Never True'. Explain your reasoning.
(i) Cube numbers are also square numbers.
(ii) Fourth powers are also square numbers.
(iii) The fifth power of a number is divisible by the cube of that number.
(iv) The product of two cube numbers is a cube number.
(v) $q^{46}$ is both a 4th power and a 6th power ( $q$ is a prime number).

Answer:

(i) Cube numbers are also square numbers
This statement is Only Sometimes True.
(e.g., 64 is both, but 27 is not)

(ii) Fourth powers are also square numbers
This statement is Always True.
(E.g., $a^4 = (a^2)^2$)

(iii) Fifth power is divisible by a cube
This statement is Always True.
(E.g., $a^5 \div a^3 = a^2$ is always an integer)

(iv) Product of cube numbers is a cube number
This statement is Always True.
(E.g., $a^3 \times b^3 = (ab)^3$)

(v) $q^{46}$ is both 4th and 6th power (q is prime)
This statement is never true.
A number is both a 4th and a 6th power if its exponent is a multiple of $\operatorname{LCM}(4,6)=12$.
Since $46=2 \times 23$ (not divisible by 4 or 6 )
But the question says $q^{46}$ is both a 4th and a 6th power. That's impossible unless 46 is divisible by both 4 and 6.

Question 5. Simplify and write these in the exponential form.
(i) $10^{-2} \times 10^{-5}$
(ii) $5^7 \div 5^4$
(iii) $9^{-7} \div 9^4$
(iv) $\left(13^{-2}\right)^{-3}$
(v) $m^5 n^{12}(m n)^9$

Answer:

(i) $10^{-2} \times 10^{-5}=10^{-2+(-5)} = 10^{-7}$

(ii) $5^7 \div 5^4=5^{7-4} = 5^{3}$

(iii) $9^{-7} \div 9^4=9^{-7-(+4)} = 9^{-11}$

(iv) $(13^{-2})^{-3}=(-13)^{-2\times-3} = 13^{6}$

(v) $m^5 n^{12}(m n)^9=m^5 n^{12}m^9n^9= m^{(5+9)} n^{(12+9)} = m^{14} n^{21}$

Question 6. If $12^2=144$ what is
(i) $(1.2)^2$
(ii) $(0.12)^2$
(iii) $(0.012)^2$
(iv) $120^2$

Answer:

(i) $(1.2)^2 = 1.2\times1.2=1.44$

(ii) $(0.12)^2 = 0.12 \times 0.12=0.0144$

(iii) $(0.012)^2 = 0.012\times0.012=0.000144$

(iv) $(120)^2 = 120\times120=14400$

Question 7. Circle the numbers that are the same-
$2^4 \times 3^6$
$6^4 \times 3^2$
$6^{10}$
$18^2 \times 6^2$
$6^{24}$

Answer:

After simplifying, we get,

• $2^4 \times 3^6$
• $6^4 \times 3^2=(2 \times 3)^4 \times 3^2=2^4 \times 3^4 \times 3^2=2^4 \times 3^6$
• $6^{10}=(2 \times 3)^{10}=2^{10} \times 3^{10}$
• $18^2 \times 6^2=\left(2 \times 3^2\right)^2 \times(2 \times 3)^2=2^2 \times 3^4 \times 2^2 \times 3^2=2^4 \times 3^6$
• $6^{24}=(2 \times 3)^{24}=2^{24} \times 3^{24}$

$\therefore$ $\left(2^4 \times 3^6\right),\left(6^4 \times 3^2\right)$ and $\left(18^2 \times 6^2\right)$ are same.

Question 8. Identify the greater number in each of the following-
(i) $4^3$ or $3^4$
(ii) $2^8$ or $8^2$
(iii) $100^2$ or $2^{100}$

Answer:

(i) $4^3 = 64$, $3^4 = 81$ → 34 is greater.

(ii) $2^8 = 256$, $8^2 = 64$ → 28 is greater.

(iii) $100^2 = 10000$, $2^{100}$ = massive → 2100 is greater.

Question 9. A dairy plans to produce 8.5 billion packets of milk in a year. They want a unique ID (identifier) code for each packet. If they choose to use the digits $0-9$, how many digits should the code consist of?

Answer:

A dairy plans to produce 8.5 billion $=8.5 \times 10^9$ packets.

Each packet needs a unique numeric code using digits 0-9.

The number of unique codes that can be made with $n$ digits $=(10)^n$

We must find the smallest n such that: $10^n \geq 8.5 \times 10^9$

If we put $n=9$, we get:

$10^9=1,000,000,000$ less than 8.5 billion.

If we put $n=10$, we get:

$10^{10}=10,000,000,000$ more than 8.5 billion.

So, the code must have at least 10 digits, since $10^{10}$ is the smallest power of 10 greater than 8.5 billion.

Question 10. 64 is a square number $\left(8^2\right)$ and a cube number $\left(4^3\right)$. Are there other numbers that are both squares and cubes? Is there a way to describe such numbers in general?

Answer:

Examples of such numbers:

• $1=1^2=1^3$
• $64=8^2=4^3$
• $729=27^2=9^3$
• $4096=64^2=16^3$
• $15625=125^2=25^3$

Numbers that are both perfect squares and cubes are 6th powers are 6th powers: $n^6$
Example:

• $1^6 = 1$
• $2^6 = 64$
• $3^6 = 729$
• $4^6 = 4096$

Question 11. A digital locker has an alphanumeric (it can have both digits and letters) passcode of length 5. Some example codes are G89P0, 38098, BRJKW, and 003AZ. How many such codes are possible?

Answer:

Each passcode is 5 characters long, and each character can be alphanumeric, i.e., A-Z (26 letters) and 0-9 (10 digits)
So, total choices per position $=26+10=36$
Now, each of the 5 positions in the code can be filled in 36 ways.
So, total number of such codes $=36 \times 36 \times 36 \times 36 \times 36=36^5$
Thus, $36^5=60,466,176$

Hence, the answer is $60,466,176$.

Question 12. The worldwide population of sheep (2024) is about $10^9$, and that of goats is also about the same. What is the total population of sheep and goats?
(ii) $20^9$
(ii) $10^{11}$
(iii) $10^{10}$
(iv) $10^{18}$
(v) $2 \times 10^9$
(vi) $10^9+10^9$

Answer:

The worldwide population of sheep (2024) is about 10⁹, and that of goats is also about the same.
So, Tota population $10^9 + 10^9 = 2 \times 10^9$

Hence, both options (v) $2 \times 10^9$ and (vi) $10^9 + 10^9$ are correct.

Question 13. Calculate and write the answer in scientific notation:
(i) If each person in the world had 30 pieces of clothing, find the total number of pieces of clothing.
(ii) There are about 100 million bee colonies in the world. Find the number of honeybees if each colony has about 50,000 bees.
(iii) The human body has about 38 trillion bacterial cells. Find the bacterial population residing in all humans in the world.
(iv) Total time spent eating in a lifetime in seconds.

Answer:

(i) World population ≈ $8 \times 10^9$
Each has 30 clothes → $8 \times 10^9 \times 30 = 2.4 \times 10^{11}$

(ii) 100 million = $10^8$ colonies
50,000 = $5 \times 10^4$
→ $10^8 \times 5 \times 10^4 = 5 \times 10^{12}$

(iii) World population $\approx 8 \times 10^9$ (approx.)
The human body has bacterial cells $=38$ trillion
$\begin{aligned}
& 38 \text { trillion }=3.8 \times 10^{13} \\
& \text { So, total Bacteria }=\left(8 \times 10^9\right) \times\left(3.8 \times 10^{13}\right) \\
& =30.4 \times 10^9 \times 10^{13} \\
& =30.4 \times 10^{22} \\
& =3.04 \times 10^{23}
\end{aligned}$

(iv) Average eating time per day $=1.5$ hours
$
=1.5 \times 60 \times 60=5400 \text { seconds }
$
Average lifespan $=70$ years
Number of days in 70 years $=70 \times 365=25,550$ days
Total eating time in lifespan:
$\begin{aligned}
& =(5400) \times 25,550 \\
& =137,970,000 \text { seconds } \\
& =1.3797 \times 10^3 \text { seconds }
\end{aligned}$

Question 14. What was the date $1\ \mathrm{arab} / 1$ billion seconds ago?

Answer:

1 billion = $10^9$ seconds
Converting to years, we get,
$10^9 \div (60 \times 60 \times 24 \times 365.25) \approx 31.7$ years

If today = August 4, 2025 →
1 billion seconds ago ≈ December 2003

NCERT Power Play Class 8 Chapter 2: Topics

The topics discussed in the NCERT Solutions for Class 8 Chapter 2 Power Play are:

• Experiencing the Power Play
• Exponential Notation and Operations
• The Other Side of Powers
• Power Lines
• Powers of 10
• Did You Ever Wonder?
• Linear Growth vs. Exponential Growth
• Getting a Sense for Large Numbers
• A Pinch of History

Class 8 Maths Chapter 2 Power Play Solutions: Extra Question

Question:

What is the value of ‘a’ in the equation below?
{(5 × 5 × 5 × 5 × 5 × 5)⁵ × (5 × 5 × 5 × 5 × 5)⁸} ÷ (5 × 5) = (625)^a

Solution:

Given:
{(5 × 5 × 5 × 5 × 5 × 5)⁵ × (5 × 5 × 5 × 5 × 5)⁸} ÷ (5 × 5) = (625)^a
⇒ {(5⁶)⁵} × (5⁵)⁸} ÷ (5²) = (625)^a
⇒ {5³⁰ × 5⁴⁰} ÷ 5² = 625^a
⇒ 5^{(30 + 40 – 2)} = (5⁴)^a
⇒ 5^4a = 5⁶⁸
⇒ 4a = 68
$\therefore$ a = 17
Hence, the correct answer is 17.

NCERT Solutions for Class 8 Maths Chapter 2 Power Play: Notes

Careers360 has prepared these Power Play Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Power Play NCERT solutions and solve them on their own from next time.

Exponents of a real number represent the multiplication of the base number. They can be positive, negative, zero or fractional.

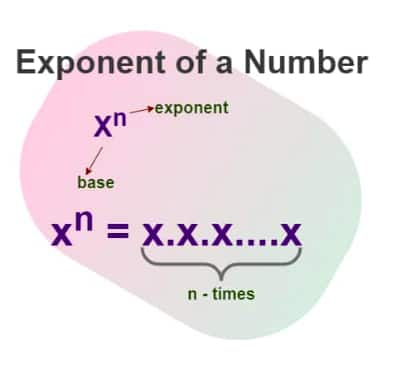
Here are some of the types of exponents.

• Positive exponents
• Negative exponents
• Zero exponents
• Rational exponents

Positive Exponents

If an exponent indicates how many times a number is multiplied by itself, it is called a Positive exponent.

Example:

3 × 3 × 3 = 3³ = 9

Here, 3³ shows how many times the number 3 is multiplied by itself. So it is a Positive exponent.

Negative Exponents

If an exponent represents the reciprocal of the base raised to the absolute value of the exponent, then it is called a Negative exponent.

Example:

3^-3 = $\frac{1}{3^3}=\frac{1}{9}$

Zero Exponent

Any number with an exponent of zero has a value equal to 1.

Example:

5⁰ = 1, 10⁰ = 1, (–3)⁰ = 0, etc.

Rational Exponents

Rational exponents are also known as Fractional exponents. It represents both roots and powers.

The general form of a rational exponent is:
$a^{\frac{m}{n}}=\sqrt[n]{a^m}$
Here, $a$ is the base, $m$ is the power, and $n$ is the root.

Example: $16^{\frac{3}{4}}=(\sqrt[4]{16})^3=2^3=8$

Linear Growth vs. Exponential Growth

Here are the differences between linear and exponential growth.

Large Numbers and Their Examples

NCERT Solutions for Class 8 Maths Chapter 2 Power Play: Important Formulae

Here are some important formulae or laws that will help students to solve problems related to Class 8 Maths NCERT Chapter 2 Power Play.

• Law of Product: $a^m \times a^n=a^{(m+n)}$
• Law of Quotient: $\frac{a^m}{a^n}=a^{(m-n)}$
• Law of Zero Exponent: $a^{0} = 1$
• Law of Negative Exponent: $a^{(-m)}= \frac{1}{ a^m}$
• Law of Power of a Power: $\left(a^m\right)^n=a^{\left(mn\right)}$
• Law of Power of a Product: $(a b)^n=a^{n} b^n$
• Law of Power of a Quotient: $(\frac{a}{b})^m= \frac{a^m}{b^m}$

NCERT Solutions for Class 8 Mathematics - Chapter Wise

We at Careers360 compiled all the class 8 Maths solutions in one place for easy student reference. This page gives you direct access to all NCERT Class 8 Maths solutions, without the hassle of searching around.

NCERT Books and NCERT Syllabus

The following links will give students access to the latest NCERT syllabus and some reference books.

• NCERT Books Class 8 Maths
• NCERT Syllabus Class 8 Maths
• NCERT Books Class 8
• NCERT Syllabus Class 8