NCERT Exemplar Class 12 Physics Solutions Chapter 9 Ray Optics and Optical Instruments
Have you ever seen your face as inverted when looking into a spoon? This is a common effect of reflection that occurs on a curved (concave) mirror, concept which will be discussed in Chapter 9 Ray Optics and Optical instruments of NCERT Exemplar Class 12 Physics. The chapter reveals the way light propagates, reflects and refracts through various media and with optical instruments.Students will explore in-depth the image formation by a spherical mirror and lens, equation of mirrors, refraction, and total internal reflection, and how these principles find useful applications with on mirages and optical fibres. There is also a look at practical applications of optical instruments life the human eye, microscopes and telescopes and this means not only theoretically but also practically in an optical vision.
This Story also Contains
- NCERT Exemplar Class 12 Physics Solutions Chapter 9 MCQ I
- NCERT Exemplar Class 12 Physics Solutions Chapter 9 MCQ II
- NCERT Exemplar Class 12 Physics Solutions Chapter 9 Very Short Answer
- NCERT Exemplar Class 12 Physics Solutions Chapter 9 Short Answer
- NCERT Exemplar Class 12 Physics Solutions Chapter 9 Long Answer
- NCERT Exemplar Class 12 Physics Solutions Chapter 9 Ray Optics and Optical Instruments - Main Subtopics
- NCERT Exemplar Class 12 Physics Chapter Wise Links

The NCERT Exemplar Class 12 Physics solutions of Chapter 9 provide step by step explanation of all the questions and hence helps the student easily work out the complicated numerical problems. The exemplar solutions are properly designed keeping in mind a choice of questions (MCQs), short answer, long answer, and very long answer and so, they allow the students to approach all varieties of examination questions with confidence. Being both CBSE board and competition exam (JEE and NEET) appropriate, this resource perfects fundamental concepts and provides a rigorous revision by including solved examples, derivations, and practice questions
Also, see NCERT Solutions for Class 12 Physics
NCERT Exemplar Class 12 Physics Solutions Chapter 9 MCQ I
Question:9.1
A ray of light incident at an angle on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5° and the prism is made of a material of a refractive index 1.5, the angle of incidence is
A. $7.5^{o}$
B. $5^{o}$
C.$15^{o}$
D. $2.5^{o}$
Answer:
The correct answer is the option (A) $7.5^{o}$
As it is a thin prism, the distance between the refracting surfaces is non-accountable and (A), the prism angle is also very small. Since angle (A) is small, it implies that both $r_{1}$ and $r_{2}$ are also small.
According to snell's law,
1 $\sin i_{1}=\mu \; \sin r_{1}\Rightarrow i_{1}=\mu\; r_{1}$
Also, 1 $\sin i_{2}=\mu \; \sin r_{2}\Rightarrow i_{2}=\mu\; r_{2}$
Therefore, deviation,
$\delta =\left ( i_{1}-r_{1} \right )+\left ( i_{2}-r_{2} \right )$
$\Rightarrow \; \; \; \; \delta =\left ( i_{1}+i_{2} \right )-\left ( r_{1}+r_{2} \right )=\left ( r_{1}+r_{2} \right )\left ( \mu -1 \right )$
$\Rightarrow \delta =A\left ( \mu -1 \right )$
Since, deviation $\delta =A\left ( \mu -1 \right )A$
$\delta=\left ( 1.5-1 \right )\times 5^{o}=2.5^{o}$
The angle of the prism is $5^{o}$. The ray emrerges from refracting face of a prism normally.
Then, $i_{2}=r_{2}=0$
As $A= r_{1}+r_{2}\Rightarrow r_{i}=A\; or\; r_{1}=5^{o}$
But $i_{1}=\mu .r_{1}=\frac{3}{2}\times 5=7.5^{o}$
Question:9.2
A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is
A. blue
B. green
C. violet
D. red
Answer:
The correct answer is the option (D)
The emerging colour would be red, because of the relation $v=f\lambda ,$ which provides the velocity of a wave. During the changing of the mediums, the frequency of the wave remains constant. So, $v\; \alpha \lambda$ or wavelength is directly proportional to speed. As red colour has the highest wavelength in the spectra, it also has the highest speed according to tot eh relation. Hence, when the light travels in the slab, the first colour to emerge is red.
Question:9.3
An object approaches a convergent lens from the left of the lens with a uniform speed 5 m/s and stops at the focus. The image
A. moves away from the lens with a uniform speed 5 m/s.
B. moves away from the lens with uniform acceleration.
C. moves away from the lens with a non-uniform acceleration.
D. moves towards the lens with a non-uniform acceleration.
Answer:
The correct answer is the option (C).
The image will moves away from the lens with a non-uniform acceleration), in this case, the objects are moving with a uniform speed of 5 m/s towards a convergent lens from the left, thus with a non-uniform acceleration, the image moves away from the lens. The image starts at a uniform speed but gets accelerated going from 2F to F; the image goes from 2F to infinity. When the image is at 2F, both the object and image will have the same speed.
Question:9.4
A passenger in an aeroplane shall
A. never see a rainbow.
B. may see a primary and a secondary rainbow as concentric circles.
C. may see a primary and a secondary rainbow as concentric arcs.
D. shall never see a secondary rainbow.
Answer:
The answer is the option (B)A passenger has an aeroplane has the possibility to see a primary and a secondary rainbow as concentric circles because the plane is at an extremely high altitude.
In case of an object moving towards the convex lens with a constant speed from infinity to focus, the image will move slower in the beginning and then faster.
$v_{i}=\left ( \frac{f}{f+u} \right )^{2}v_{o}$
And if an object approaches the lens, the image moves away from the lens with a non-uniform acceleration.
Question:9.5
You are given four sources of light each one providing a light of a single colour – red, blue, green and yellow. Suppose the angle of refraction for a beam of yellow light corresponding to a particular angle of incidence at the interface of two media is 90°. Which of the following statements is correct if the source of yellow light is replaced with that of other lights without changing the angle of incidence?
A.The beam of red light would undergo total internal reflection.
B. The beam of red light would bend towards normal while it gets refracted through the second medium.
C. The beam of blue light would undergo total internal reflection.
D. The beam of green light would bend away from the normal as it gets refracted through the second medium.
Answer:
The correct answer is the option (C).
The beam of blue light would undergo total internal reflection, so option (c) is the correct answer.
According to the Cauchy relationship, smaller the wavelength higher the refractive index and consequently smaller the critical angle
We know $v=f\lambda,$ the frequency of wave remains unchanged with medium hence $v\alpha \lambda$
The critical angle,
$\sin \; C=\frac{1}{\mu }$
Also, velocity of light,
$v\alpha \frac{1}{\mu }$
According to VIBGYOR, among all given sources of light, the blue light have the smallest wavelength.
As $\lambda _{blue}<\lambda _{yellow}$, hence $v _{blue}<v _{yellow}$, it means $\mu _{blue}<\mu _{yellow}$
It means the critical angle for blue is less than yellow colour, the critical angle is the least, which facilitates total internal reflection for the beam of blue light.
Question:9.6
The radius of curvature of the curved surface of a Plano-convex lens is 20 cm. If the refractive index of the material of the lens be 1.5, it will
A. act as a convex lens only for the objects that lie on its curved side.
B. act as a concave lens for the objects that lie on its curved side.
C. act as a convex lens irrespective of the side on which the object lies.
D. act as a concave lens irrespective of side on which the object lies.
Answer:
The correct answer is the option (C) act as a convex lens irrespective of the side on which the object lies
Key concept : The relation between $f,\mu ,R_{1}$ and $R_{2}$ is known as lens maker's formula and it is
$\frac{1}{f}=\left ( \mu -1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$
$R_{1}=\infty ,R_{2}=-R$
$f=\frac{R}{\left ( \mu -1 \right )}$
Here, R=20 cm, $\mu =1.5$.
On substituting the values, we get
$f=\frac{R}{\mu -1}=\frac{20}{15-1}=40\; cm$
As $f>0$ means converging nature.
Therefore, the lens acts as a convex lens irrespective of the side on which the object lies.
Question:9.7
The phenomenon involved in the reflection of radio waves by ionosphere is similar to
A. reflection of light by a plane mirror.
B. total internal reflection of light in air during a mirage.
C. dispersion of light by water molecules during the formation of a rainbow.
D. scattering of light by the particles of air.
Answer:
The correct answer is the option (B)The phenomena are very similar to total internal reflection of light in the air during a mirage. The Ionosphere layer of atmosphere around earth is responsible for reflecting the radio waves. And as the angle of incidence is greater than critical, it is very similar to total internal reflection of light in the air during a mirage.
Question:9.8
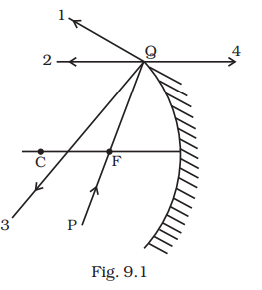
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
The correct answer is the option (B)
The ray PQ incident to the concave mirror passes through the focus F, after reflection, as shown in the diagram is supposed to be parallel to the principal axis.
Important Note:
To find out the exact extended graphical location of the image of any object, one can draw any of the given two rays:
1. Draw a ray reflected through the focus of the mirror, which is initially parallel to the principal axis (1).
2. When a ray is drawn through the centre of curvature, it reflects back along with itself (3).
3. Draw a ray that is initiated through the focus; it will be reflected parallel to the principal axis (2).
4. A ray drawn incident to the pole gets reflected back in a symmetrical manner.
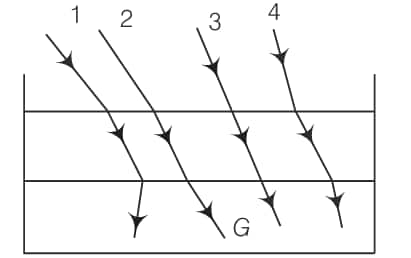
Question:9.9
Fig 9.2
A. 1
B. 2
C. 3
D. 4
Answer:
The correct answer is the option (B)
The Snell's law describes the relationship between the angle of incidence and the angle of refraction.
$\mu _{1}\sin \theta_{1}=\mu _{2}\sin \theta_{2}=\text {Constant}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ....(1)$
Where $\mu _{1}\; \text {and}\; \mu _{2}$ are refractive indices of the two media.
In this diagram, the ray of light is going from an optically rarer medium to turpentine which an optically denser medium, then the ray bends towards the normal, which means $\theta _{1}> \theta _{2}$, but when it goes in the opposite direction, i.e. optically denser medium turpentine to rarer medium water, the ray bends away from the normal.
Question:9.10
A car is moving at a constant speed of $60\; km\; h^{-1}$ on a straight road. Looking at the rearview mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of $5\; km\; h^{-1}$. In order to keep track of the car in the rear, the driver begins to glance alternatively at the rear and side mirror of his car after every 2 s till the other car overtakes. If the two cars were maintaining their speeds, which of the following statement (s) is/are correct?
A. The speed of the car in the rear is $65\; km\; h^{-1}$.
B. In the side mirror the car in the rear would appear to approach with a speed of $5\; km\; h^{-1}$ to the driver of the leading car.
C. In the rearview mirror the speed of the approaching car would appear to decrease as the distance between the cars decreases.
D. In the side mirror, the speed of the approaching car would appear to increase as the distance between the cars decreases.
Answer:
The correct answer is the option (A).When an object is placed in front of a mirror, all the positions of objects in the front of a mirror, image is virtual, erect and smaller in size. And as the object moves towards the pole, magnification increases and tends to unity at the pole.

An object moving along the principal axis – on differentiating the mirror formula with respect to time we get,
$\frac{dv}{dt}=-\left ( \frac{v}{u} \right )^{2}\frac{du}{dt}=-\left ( \frac{f}{u-f} \right )^{2}\frac{du}{dt}$
where $\frac{dv}{dt}$ is the velocity of the image moving along the principal axis, and $\frac{du}{dt}$ is the velocity of the object along the principal axis. The negative sign indicates that the image always moves in the direction opposite to that of the object
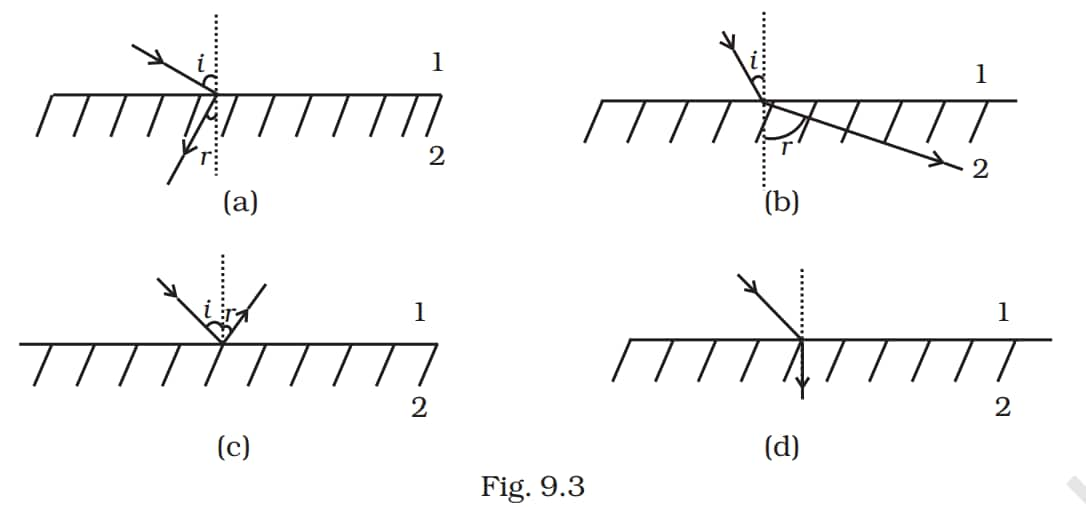
Question:9.11
Answer:
The correct answer is the option (A)
When a material has a negative refractive index, it follows the Snell's law in an opposite manner. And when an incident ray from one medium (air) falls on them, it bends just the way shown in option (a) that is on the same side of the normal.
NCERT Exemplar Class 12 Physics Solutions Chapter 9 MCQ II
Question:9.12
Consider an extended object immersed in water contained in a plane trough. When seen from close to the edge of the trough, the object looks distorted because
A. the apparent depth of the points close to the edge are nearer the surface of the water compared to the points away from the edge.
B. the angle subtended by the image of the object at the eye is smaller than the actual angle subtended by the object in air.
C. some of the points of the object far away from the edge may not be visible because of total internal reflection.
D. water in a trough acts as a lens and magnifies the object.
Answer:
The correct answers are the options (A,B,C)When the ray of light passes from water into the air from the pencil it is refracted, the beam bends away from the normal when going from high to low refractive index.
In case of light getting refracted from the water surface from the submerged object before reaching the observer, it bends away from the normal and the angle formed by the image of the object is smaller than the real angle formed by the object in the air. This also affects the apparent depth as it becomes nearer to the surface of the water when points are close to the edge as compared to the points far from the edge.
The angle of incidence increases while moving right, and it becomes equal to the critical angle. Thus, due to total internal reflection, some points of the object present far from the edge may not be visible.
Question:9.13
A rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the face AB (Fig. 9.4). When observed from the face AD, the pin shall
A. appear to be near A.
B. appear to be near D.
C. appear to be at the centre of AD.
D. not be seen at all.
Answer:
The correct answers are the options (A, D)
As long as angle of incidence on AD of the ray emanating from the pin is less than the critical angle, the pin shall appear to be near A.
When angle of incidence on AD of the ray emanating from pins is greater than the critical angle, the light suffers from total internal reflection and cannot be seen through AD .
Question:9.14
Between the primary and secondary rainbows, there is a dark band known as Alexandra’s dark band. This is because
A. light scattered into this region interfere destructively.
B. there is no light scattered into this region.
C. light is absorbed in this region.
D. angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
Answer:
The correct answers are the options (A,D)
Alexandar's dark band lies between the primary and secondary rainbows, formed due to light scattered into this region interfere destructively.
Since, primary rainbows subtends an angle nearly $41^{\circ}$ to $42^{\circ}$ at observer's eye, whereas, secondary rainbows subtends an angle nearly $51^{\circ}$ to $54^{\circ}$ at observer's eye w.r.t. incident light ray.
So, the scattered rays with respect to the incident light of the sun lie between approximately $42^{\circ}$ and $50^{\circ}$.
Question:9.15
A magnifying glass is used, as the object to be viewed can be brought closer to the eye than the normal near point. This results in
A. a larger angle to be subtended by the object at the eye and hence viewed in greater detail.
B. the formation of a virtual erect image.
C. increase in the field of view.
D. infinite magnification at the near point.
Answer:
The correct answers are the options (A, B)A magnifying glass simply contains a convex lens of very small focal length.

For magnification when the final image is formed at D and $\infty$ $\left ( \text {i.e}, m_{D}\; \text {and}\; m_{\infty } \right ).$
$m_{D}=\left ( 1+\frac{D}{f} \right )_{max}$ and $m_{\infty }=\left (\frac{D}{f} \right )_{min}$
By using a magnifying glass, any objects can be brought closer to the eye as compared to the normal near point. The angle formed by the object in the eye is larger and thus, is more detailed. The image formed is virtual erect and is also enlarged.
Question:9.16
An astronomical refractive telescope has an objective of focal length 20m and an eyepiece of focal length 2cm.
A. The length of the telescope tube is 20.02m.
B. The magnification is 1000.
C. The image formed is inverted.
D. An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
Answer:
The correct answers are the options (A,B and C)
Key concept :
- Use to see heavenly bodies.
- $f_{objective}>f_{eye\; lens}$ and $d_{objective}>d_{eye\; lens}$
- The intermediate image is real, inverted and small.
- The final image is virtual, inverted and small.
- Magnification:
- $m_{D}=-\frac{f_{0}}{f_{e}}\left ( 1+\frac{f_{e}}{D} \right )$and $m_{\infty }=-\frac{f_{0}}{f_{e}}$
- Length :
- $L_{D}=f_{0}+u_{e}=f_{0}+\frac{f_{e}D}{f_{e}+D}$and $L_{\infty }=f_{0}+f_{e}$
The length of the telescope tube is
$f_{0}+f_{e}=20+(0.02)=20.02\; m$
Also,
$m=\frac{20}{0.02}=1000$
Also, the image formed is inverted.
NCERT Exemplar Class 12 Physics Solutions Chapter 9 Very Short Answer
Question:9.17
Will the focal length of a lens for red light be more, same or less than that for blue light?
Answer:
The refractive index depends on the colour of light or wavelength of light.Cauchy's equation : $\mu =A+\frac{B}{\lambda ^{2}}+\frac{C}{\lambda ^{4}}+......$
As $\lambda _{red}>\lambda _{blue}$, hence $\mu _{red}<\mu _{blue}$
Hence parallel beams of light incident on a lens will be bent more towards the axis for blue light compared to red.
By lens maker's formula,
$\frac{1}{f}=\left ( \mu -1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$
The refractive index for red light is less than that for blue light, $\mu _{red}<\mu _{blue}$
Hence $\frac{1}{f_{red}}<\frac{1}{f_{blue}}\Rightarrow f_{red}>f_{blue}$
Thus, the focal length for red light will be greater than that for blue light.
Question:9.18
Answer:
In the given question, the least distance of distinct vision of an average person is 25 cm, in order to view an object with magnification 10,Here,
$v=D=25\; cm\; and\; u=f$
But the magnification
$m=\frac{v}{u}=\frac{D}{f}$
$\Rightarrow f=\frac{D}{m}=\frac{25}{10}=2.5 \; cm=0.025\; m$
But power
$P=\frac{1}{f(in\; m)}=\frac{1}{0.025}=40\; D$
This is the required power of the lens.
Question:9.19
Answer:
For a given object position if the focal length of the lens does not change, the image position remains unchanged.
By lens maker's formula,
$\frac{1}{f}=\left ( \mu -1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$
For this position $R_{1}$ is positive
and $R_{2}$ is negative. Hence focal length at this position
$\frac{1}{f_{1}}=\left ( \mu -1 \right )\left ( \frac{1}{\left ( +R_{1} \right )}-\frac{1}{\left ( -R_{2} \right )} \right )=\left ( \mu -1 \right )\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}} \right )$
Now the lens is reversed,
At this position, $R_{2}$ is positive and $R_{1}$ is negative. Hence focal length at this position is
$\frac{1}{f_{2}}=\left ( \mu -1 \right )\left ( \frac{1}{\left ( +R_{2} \right )}-\frac{1}{\left ( -R_{1} \right )} \right )=\left ( \mu -1 \right )\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}} \right )$
We can observe the focal length of the lens does not change in both positions, hence the image position remains unchanged.
Question:9.20
Answer:

\begin{aligned}
&\text { Let the apparent depth be } \mathrm{O}_1 \text { for the object seen from } m_2 \text {, then }\\
&\mathrm{O}_1=\frac{\mu_2}{\mu_1} \frac{h}{3}
\end{aligned}
Since, apparent depth $=$ real depth /refractive index $\mu$.
Since, the image formed by Medium $1, \mathrm{O}_2$ act as an object for Medium 2.
If seen from $\mu_3$, the apparent depth is $\mathrm{O}_2$.
Similarly, the image formed by Medium $2, \mathrm{O}_2$ act as an object for Medium 3
$
\begin{aligned}
O_2 & =\frac{\mu_3}{\mu_2}\left(\frac{h}{3}+O_1\right) \\
& =\frac{\mu_3}{\mu_2}\left(\frac{h}{3}+\frac{\mu_2 h}{\mu_1 3}\right)=\frac{h}{3}\left(\frac{\mu_3}{\mu_2}+\frac{\mu_2}{\mu_1}\right)
\end{aligned}
$
Seen from outside, the apparent height is
$
\begin{aligned}
O_3 & =\frac{1}{\mu_3}\left(\frac{h}{3}+O_2\right)=\frac{1}{\mu_3}\left[\frac{h}{3}+\frac{h}{3}\left(\frac{\mu_3}{\mu_2}+\frac{\mu_3}{\mu_1}\right)\right] \\
& =\frac{h}{3}\left(\frac{1}{\mu_1}+\frac{1}{\mu_2}+\frac{1}{\mu_3}\right)
\end{aligned}
$
This is the required expression of apparent depth.
Question:9.21
Answer:
The refractive index of prism angle A and angle of minimum deviation $\delta _{m}$ is given by
$\mu=\frac{\sin\left [ \frac{\left ( A+\delta _{m} \right )}{2} \right ]}{\sin\left ( \frac{A}{2} \right )}$
Here we are given, $\delta _{m}=A$
Substituting the value, we have
$\mu=\frac{\sin A}{\sin \frac{A}{2}}$
$\Rightarrow \mu=\frac{2\sin\frac{A}{2}\cos\frac{A}{2}}{\sin\frac{A}{2}}=2 \cos\frac{A}{2}$
$\Rightarrow \mu=\frac{\sin A}{\sin \frac{A}{2}}=\frac{2\sin\frac{A}{2}\cos\frac{A}{2}}{\sin\frac{A}{2}}=2 \cos\frac{A}{2}$
For the given value of refractive index,
We have, $\cos\frac{A}{2}=\frac{\sqrt{3}}{2}\Rightarrow \frac{A}{2}=30^{o}$
Or $A=60^{o}$
This is the required value of the prism angle.
NCERT Exemplar Class 12 Physics Solutions Chapter 9 Short Answer
Question:9.22
Answer:
Thin mirror formula :
$\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$
$u=$ object distance and $v=$ image distance
Since, the object distance is ,$u$. Let us consider the two ends of the object be at distance $u_{1}$ and $u_{2}$ respectively, so that $du=\left | u_{1}-u_{2} \right |=L.$ Hence size of the image can be written as $dv$.
By differentiating both sides
$\left ( -\frac{du}{u^{2}} \right )+\left ( -\frac{dv}{v^{2}} \right )=0\Rightarrow \frac{dv}{v^{2}}=-\frac{du}{u^{2}}$
or
$dv=-\left ( \frac{v^{2}}{u^{2}} \right )du \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ...(i)$
As $\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\Rightarrow v=\frac{fu}{u-f}$
Or $\frac{v}{u}=\frac{f}{u-f} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ...(ii)$
From (i) and (ii)
$dv=-\left ( \frac{f}{u-f} \right )^{2}du$
But $du=L,$
Hence the length of the image is
$\frac{f^{2}}{(u-f)^{2}}L$
This is the required expression for the length of the image.
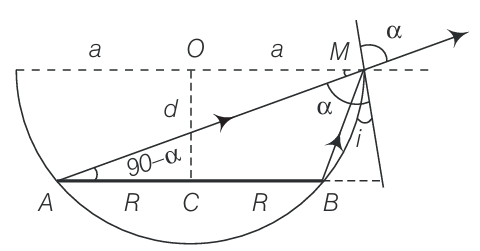
Question:9.23
Answer:
As shown in the figure, AM is in the direction of the incidence ray before filling the liquid. After filling liquid in the bowl, BM is in the direction of the incident ray. Refracted in both cases is same as that along MN.
Let the disc is separated by O at a distance d as shown in the figure. Also, considering the angle
$P=90^{o}, OM=a,CB=R,BP=a{-}R,AP=a+R$
Here, in $\Delta BMP,$
$\sin\; i=\frac{BP}{BM}=\frac{a-R}{\sqrt{d^{2}+\left ( a-R \right )^{2}}}\; \; \; \; \; \; \; \; \; \; \; ....(i)$
and
$in \Delta AMP,\; \cos \left ( 90^{o}-\alpha \right )=\sin \; \alpha =\frac{a+R}{\sqrt{d^{2}+\left ( a+R \right )^{2}}}\; \; \; \; \; \; \; \; \; \; \; \; .....(ii)$
But on applying Snell's law at point M
$\mu \times \sin \; i=1 \times \; sin \; \alpha$
$\mu \times \frac{a-R}{\sqrt{d^{2}+\left ( a-R \right )^{2}}}=1\times \frac{a+R}{\sqrt{d^{2}+\left ( a+R \right )^{2}}}$
$\Rightarrow d=\frac{\mu \left ( a^{2}-b^{2} \right )}{\sqrt{\left ( a+r \right )^{2}-\mu \left ( a-r \right )^{2}}}$
Question:9.24
Answer:
The focal length will remain the same for each of the parts in case an asymmetric lens is cut into two parts parallel to the principal axis. In such a case, the intensity of the image that has been formed by every part will be lower in comparison to that of the complete lens.If there were no cut, then the object would have been at a height of 0.5 cm from the principal axis OO'

The top part is placed at $\left ( 0,0 \right )$ and an object placed at $\left ( -50\; cm,0 \right )$. There is no effect on the focal length of the lens.

Applying the lens formula,
$\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$
$\frac{1}{v}=\frac{1}{u}+\frac{1}{f}=\frac{1}{-50}+\frac{1}{25}=\frac{1}{50}\Rightarrow v=50\; cm$
Magnification is
$m=\frac{v}{u}=-\frac{50}{50}=-1$
Therefore, the image would have been formed at 50 cm from the pole and 0.5 cm below the principal axis. Thus, with respect to the X-axis passing through the edge of the cut lens, the coordinates of the image are $(50\; cm, -1 \; cm)$.
Question:9.25
Answer:
This method is known as the "Displacement method", is also used to find the focal length of the lens in a laboratory$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$
If we take a convex lens L and place it between an object O and a screen S. The distance between the object and the screen would be D and the positions of the object and the screen are held fixed. Let the distance of position 1 from the object be $x_{1}$. Then the distance of the screen from the lens is $D-x_{1}$.

Therefore, $u=-x_{1}$ and $v=+\left ( D-x_{1} \right ).$
Placing it in the lens formula,
$\frac{1}{D-x_{1}}-\frac{1}{\left ( -x_{1} \right )}=\frac{1}{f}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; .....(i)$
At position II, let the distance of the lens from the screen be $x_{2}$. Then the distance of the screen from the lens is $D-x_{2}$
Therefore, $u=-x_{2}$ and $v=+\left ( D-x_{2} \right )$.
Placing it in the lens formula
$\frac{1}{D-x_{2}}-\frac{1}{\left ( -x_{2} \right )}=\frac{1}{f}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; .....(ii)$
Comparing Eqs. (i) and (ii), we realize that there are only two solutions:
$1.x_{1}=x_{2}; \text {or}$
$2.D-x_{1}=x_{2}; \text {and}\; D-x_{2}=x_{1}$
The first solution is trivial. Therefore, if the first position of the lens, for a sharp image, is $x_{1}$ fro the object, the second position is at $D-x_{1}$ from the object.
Let the distance between the two positions I and II be d.
From the diagram, it is clear that
$D=x_{1}+x_{2}\; \text {and}\; d=x_{2}-x_{1}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ...(iii)$
On solving, two equations in (iii) we have
$x_{1}=\frac{D-d}{2}$ and $D-x_{1}=\frac{D+d}{2}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ...(iv)$
Substituting Eq. (iv) in Eq. (i), we get
$\frac{1}{\left ( \frac{D+d}{2} \right )}-\frac{1}{\left ( -\frac{D-d}{2} \right )}=\frac{1}{f}\Rightarrow f=\frac{D^{2}-d^{2}}{4D}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ...(v)$
or $d=\sqrt{D^{2}-4Df}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; .....(vi)$
If $u=\frac{D}{2}+\frac{d}{2}$, then the image is at $v=\frac{D}{2}-\frac{d}{2}$.
$\therefore$ The magnification $m_{1}=\frac{D-d}{D+d}$
If $u=\frac{D-d}{2},$ then $v=\frac{D+d}{2},$
$\therefore$ The magnification $m_{2}=\frac{D+d}{D-d}$
Thus, $\frac{m_{2}}{m_{1}}=\left ( \frac{D+d}{D-d} \right )^{2}$
This is the required expression of magnification.
Question:9.26
Fig 9.6
Answer:
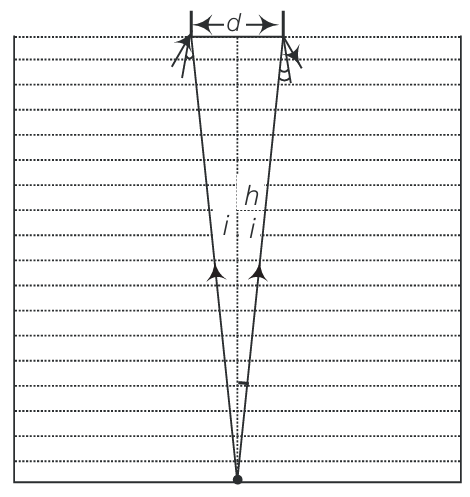
Let $d$ be the diameter of the disc. The spot shall be invisible if the incident rays from the dot at $O$ to the surface at $d / 2$ at the critical angle.
Let $i$ be the angle of incidence.
Using relationship between refractive index and critical angle, then,
$
\sin i=\frac{1}{\mu}
$
Using geometry and trigonometry.
$
\begin{array}{ll}
\text { Now, } & \frac{d / 2}{h}=\tan i \\
\Rightarrow & \frac{d}{2}=h \tan i=h\left[\sqrt{\mu^2-1}\right]^{-1} \\
\therefore & d=\frac{2 h}{\sqrt{\mu^2-1}}
\end{array}
$
This is the required expression of $d$.
Question:9.27
Answer:
(i) If for the normal relaxed eye of an average person, the power at the far point be $P_{f}$. The required power
$P_{f}=\frac{1}{f}=\frac{1}{0.1}+\frac{1}{0.02}=60\: D$
By the corrective lens, the object distance at the far point is $\infty$.
The power required is ,
$P'_{f}=\frac{1}{f'}=\frac{1}{\infty }+\frac{1}{0.02}=50\; D$
Now for eye+lens system, we have the sum of the eye and that of the glasses $P_{g}$.
$P'_{f}=P_{f}+P_{g}\Rightarrow 50\; D=60D+P_{g}$
Which gives, $P_{g}=-10D$
(ii) For the normal eye his power of accommodation is 4D. Let the power of the normal eye for near vision be $P_{n}$
Then, $4=P_{n}-P_{f}\; or \; P_{n}=64\; D$
Let his near point be $x_{n'}$ then
$\frac{1}{x_{n}}+\frac{1}{0.02}=64\;$
$or\; \frac{1}{x_{n}}+50=64$
$or, \frac{1}{x_{n}}=14$
$\Rightarrow x_{n}=\frac{1}{14}m=0.07 m$
(iii) With glasses $P_{n}^{'}=P{_{f}}^{'}+4=54$
$\Rightarrow 54=\frac{1}{x{_{n}}^{'}}+\frac{1}{0.02}=\frac{1}{x{_{n}}^{'}}+50$
$\Rightarrow \frac{1}{x{_{n}}^{'}}=4$
$\Rightarrow x{_{n}}^{'}=\frac{1}{4}m=0.25\; m$
NCERT Exemplar Class 12 Physics Solutions Chapter 9 Long Answer
Question:9.28
Answer:
Let the ray incident on face AB at angle i, after refraction, it travels along PQ and then interact with face AC which is perpendicular to the incident face.
Any ray is guided along AC if the angle ray makes with the face AC $\left ( \phi \right )$ is greater than the critical angle. From figure
$\phi +r=90^{o}$, therefore $\sin\; \phi =\cos\; r\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ......(i)$
If $\phi$ is the critical angle it means, $\sin\; \phi \geq \frac{1}{\mu }\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ......(ii)$
From (i) and (ii),
$\cos \; r \geq \frac{1}{\mu ^{2}}\;$
$or\; 1-\cos ^{2}r\leq 1-\frac{1}{\mu ^{2}}$
i.e. , $\Rightarrow \sin ^{2}r\leq 1-\frac{1}{\mu ^{2}}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; .....(iii)$
Applying Snell's law on face AB,
$1 \sin \; i=\mu \sin\; r$
Or $1 \sin^{2} \; i=\mu^{2} \sin^{2}\; r$
$\Rightarrow \sin^{2}\; r=\frac{1}{\mu ^{2}} \sin^{2}\; i\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; .....(iv)$
From (i) and (ii),
$\frac{1}{\mu ^{2}}\sin^{2}i\leq 1-\frac{1}{u^{2}}$
Or $\sin^{2}i\leq \mu ^{2}-1$
When $i=\frac{\pi }{2}$, then we have smallest angle $\phi$.
If it is greater than the critical angle, then all other angles of incidence shall be greater than the critical angle
Thus, $1\leq \mu ^{2}-1\; or \; \mu ^{2}\geq 2$
$\Rightarrow \mu \geq \sqrt{2}.$ This is the required result.
Question:9.29
Answer:
Let us consider a portion of a ray between x and $x+dx$ inside the liquid solution.Let us assume that the angle of incidence ray be $\theta$ and
Let the ray enter the thin column at the height y.
As a result of the refraction, the ray deviates from its original path and subsequently emerges at $x+dx$ with an angle
$\theta +d\theta$ and at a height $y+dy.$

From Snell's law,
$\mu \left ( y \right )\sin \theta =\mu \left ( y+dy \right )\sin\left ( \theta+d\theta \right )......(i)$

Let refractive index of the liquid at position y be $\mu (y)=\mu,$ then
$\mu\left ( y+dy \right )=\mu+\left ( \frac{d\mu}{dy} \right )dy=\mu+kdy$
Where $k=\left ( \frac{d\mu }{dy} \right )=$ refractive index gradient along the vertical dimension.
Hence from (i), $\mu \sin\theta=\left ( \mu+kdy \right )\sin \left ( \theta+d \theta \right )$
$\mu \sin\theta=\left ( \mu+kdy \right ).\left ( \sin \theta.\cos d \theta+\cos \theta. \sin d\theta \right )$
$\mu \sin\theta=\left ( \mu+kdy \right ).\left ( \sin \theta.1+\cos \theta.d \theta \right )\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; ....(ii)$
For small angle $\sin d \theta \approx d \theta \; and \; \cos d \theta\approx 1$
$\mu \sin \theta=\mu \sin \theta+kdy \; \sin \theta+\mu \cos \theta .d\theta+k\; \cos\; \theta dy.d \theta$
$kdy \sin \theta +\mu \cos \theta.d\theta=0\Rightarrow d \theta=-\frac{k}{\mu}\tan \theta dy$
But $\tan \theta=\frac{dx}{dy}\; and \: k=\left ( \frac{d\mu}{dy} \right )$
$d\theta=-\frac{k}{\mu}\left ( \frac{dx}{dy} \right )dy\Rightarrow d\theta=-\frac{k}{\mu}dx$
Integrating both sides, $\int_{0}^{\delta }d\theta =-\frac{k}{\mu}dx$
$\Rightarrow \delta =-\frac{kd}{\mu }=-\frac{d}{\mu }\left ( \frac{d\mu }{dy} \right )$
Question:9.30
Answer:
Let us consider two spherical surfaces of radius r and $r + dr$. Let the light be incident at an angle $\theta$ at surface r and $r + dr$ at an angle $\theta+d\theta$.
From Snell's Law,
$n(r)\sin \theta=n(r+dr)\sin(\theta+d\theta)=\left ( n(r)+\left ( \frac{dn}{dr} \right ) dr\right )\left ( \sin \theta.\cos \; d\theta+\cos \theta.\sin \; d\theta \right )$
$\Rightarrow n(r)\sin \theta=\left ( n(r)+\left ( \frac{dn}{dr} \right )dr \right )\left ( \sin \theta+\cos \theta.d\theta \right )$
For small angle, $\sin d\theta\approx d\theta\; and \; \cos d\theta\approx 1$
Ignoring the product of differentials
$\Rightarrow n(r)\sin \theta=n(r).\sin \theta+\left ( \frac{dn}{dr} \right )dr.\sin \theta+n(r).\cos \theta.d\theta$
or we have, $-\frac{dn}{dr}\tan \theta=n(r)\frac{d\theta}{dr}$
$\frac{2GM}{r^{2}c^{2}}\tan \theta=\left ( 1+\frac{2GM}{rc^{2}} \right )\frac{d\theta}{dr}\approx \frac{d\theta}{dr}$
$\int_{0}^{\theta_{0}}d\theta=\frac{2GM}{c^{2}}\int_{-\infty }^{\infty }\frac{\tan \theta dr}{r^{2}}$
Now, $r^{2}=x^{2}+R^{2}\; and \; \tan \theta=\frac{R}{x}$
$2rdr=2xdx$
Now substitution for integrals, we have
$\int_{0}^{\theta_{0}}d\theta=\frac{2GM}{c^{2}}\int_{-\infty }^{\infty }\frac{R}{x}\frac{xdx}{\left ( x^{2}+R^{2} \right )^{\frac{3}{2}}}$
Put $x=R\; \tan \phi$
$dx=R\; sec^{2} \phi \; d\phi$
$\therefore \theta_{0}=\frac{2GMR}{c^{2}}\int_{-\pi /2}^{\pi /2}\frac{R\; \sec ^{2}\phi d\; \phi }{R^{3}\sec ^{3}\phi }$
$\theta_{0}=\frac{2GM}{Rc^{2}}\int_{-\pi /2}^{\pi /2}\cos \phi d\; \phi =\frac{4GM}{Rc^{2}}$
$\Rightarrow \theta_{0}=\frac{4GM}{Rc^{2}}.$ This is the required proof.
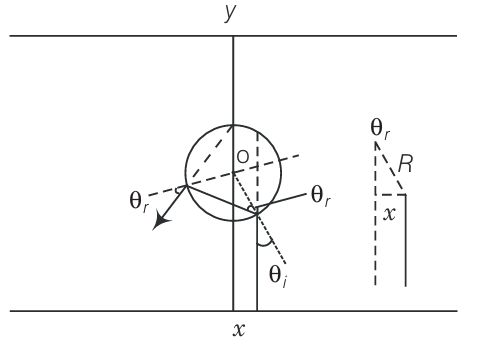
Question:9.31
Fig 9.7
Answer:
Here the material has refractive index $-1,\theta _{r}$ is negative and $\theta _{r}^{'}$ positive.
Now, $\left | \theta _{i} \right |=\left | \theta _{r} \right |=\left | \theta _{r}^{'} \right |$ The total deviation of the outcoming ray from the incoming ray is $4\theta _{r}$.
Rays shall not reach the receiving plate if
$\frac{\pi }{2}\leq 4\theta _{i}\leq \frac{3\pi }{2}$
[angles measured clockwise from the y-axis]
On solving,
$\frac{\pi }{8}\leq \theta _{i}\leq \frac{3\pi }{8}$
Now,
$\sin \theta _{i}=\frac{x}{R}$
$\frac{\pi}{8}\leq \sin^{-1}\frac{x}{R}\leq \frac{3\pi}{8}$
or $\frac{\pi}{8}\leq \frac{x}{R}\leq \frac{3\pi}{8}$
Thus, for light emitted from the source shall not reach the receiving plate,
If $\frac{R\pi}{8}\leq x\leq \frac{3R\pi }{8}$
Question:9.32
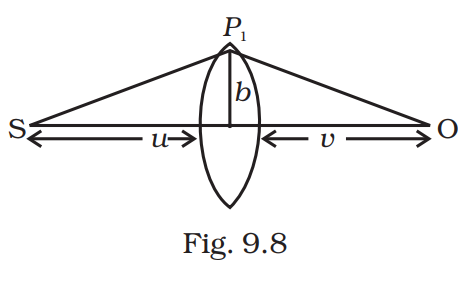
(ii) A gravitational lens may be assumed to have a varying width of the form
$\begin{aligned} w(b) & =k_1 \ln \left(\frac{k_2}{b}\right) & & b_{\min }<b<b_{\max } \\ & =k_1 \ln \left(\frac{k_2}{b_{\min }}\right) & & b<b_{\min }\end{aligned}$
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius
$\beta =\sqrt{\frac{\left ( n-1 \right )k_{1}\frac{u}{v}}{u+v}}$
Answer:

(i) The time required to travel from S to $\mathrm{P}_1$ is $t_1=\frac{S P_1}{c}=\frac{\sqrt{u^2+b^2}}{c} \simeq \frac{u}{c}\left(1+\frac{1}{2} \frac{b^2}{u^2}\right)$ assuming $\mathrm{b} \ll \mathrm{u}_0$
The time required to travel from $\mathrm{P}_1$ to O is $t_2=\frac{P_1 O}{c}=\frac{\sqrt{v^2+b^2}}{c} \simeq \frac{v}{c}\left(1+\frac{1}{2} \frac{b^2}{v^2}\right)$
The time required to travel through the lens is $t_1=\frac{(n-1) w(b)}{c}$ where n is the refractive index.
Thus the total time is
$t=\frac{1}{c}\left[u+v+\frac{1}{2} b^2\left(\frac{1}{u}+\frac{1}{v}\right)+(n-1) w(b)\right]$
Put $\frac{1}{D}=\frac{1}{u}+\frac{1}{v}$
Then $t=\frac{1}{c}\left(u+v+\frac{1}{2} \frac{b^2}{D}+(n-1)\left(w_0+\frac{b^2}{\alpha}\right)\right)$
Fermet's principle gives
$
\begin{aligned}
& \frac{d t}{d b}=0=\frac{b}{C D}-\frac{2(n-1) b}{c \alpha} \\
& \alpha=2(n-1) D
\end{aligned}
$
Thus a convergent lens is formed if $\alpha=2(n-1) D$. This is independent of $b$ and hence all paraxial rays from $S$ will converge at O (i.e. for rays $\mathrm{b} \ll \mathrm{n}$ and $\mathrm{b} \ll \mathrm{v}$ ).
Since $\frac{1}{D}=\frac{1}{u}+\frac{1}{v}$, the focal length is D .
(ii) In this case
$
\begin{aligned}
& t=\frac{1}{c}\left(u+v+\frac{1}{2} \frac{b^2}{D}+(n-1) k_1 \ln \left(\frac{k_2}{b}\right)\right) \\
& \frac{d t}{d b}=0=\frac{b}{D}-(n-1) \frac{k_1}{b} \\
& \Rightarrow \mathrm{~b}^2=(n-1) k_1 D \\
& \therefore \mathrm{~b}=\sqrt{(n-1) k_1 D}
\end{aligned}
$
\begin{aligned}
&\text { Thus all rays passing at a height } b \text { shall contribute to the image. The ray paths make an angle }\\
&\beta \simeq \frac{b}{v}=\frac{\sqrt{(n-1) k_1 D}}{v^2}=\sqrt{\frac{(n-1) k_1 u v}{v^2(u+v)}}=\sqrt{\frac{(n-1) k_1 u}{(u+v) v}} .
\end{aligned}
NCERT Exemplar Class 12 Physics Solutions Chapter 9 Ray Optics and Optical Instruments - Main Subtopics
NCERT Exemplar Class 12 Physics Solutions Chapter 9 – Ray Optics and Optical Instruments provides an in-depth understanding of the behaviour of light through reflection, refraction, and the functioning of various optical devices.
- Introduction
- Reflection of light by spherical surfaces
- Sign convention
- Focal length of spherical mirrors
- The Mirror equation
- Refraction
- Total internal reflection
- Total internal reflection in nature and its technological applications
- Refraction at spherical surfaces and by lenses
- Refraction at a spherical surface
- Refraction by a lens
- Power of a lens
- A combination of thin lenses in contact
- Refraction through a prism
- Dispersion by a prism
- Some natural phenomena due to sunlight
- The rainbow
- Scattering of light
- Optical instruments
- The eye
- The microscope
- Telescope
NCERT Exemplar Class 12 Physics Chapter Wise Links
NCERT Exemplar Class 12 Solutions
Also, check the NCERT solutions of questions given in the book
Also, read NCERT Solutions subject-wise
- NCERT Solution for Class 12 Physics
- NCERT Solution for Class 12 Chemistry
- NCERT Solution for Class 12 Maths
- NCERT Solution for Class 12 Biology
Must read NCERT Notes subject wise
- NCERT Notes for Class 12 Physics
- NCERT Notes for Class 12 Chemistry
- NCERT Notes for Class 12 Maths
- NCERT Notes for Class 12 Biology
Also, check the NCERT Books and NCERT Syllabus here:
Frequently Asked Questions (FAQs)
This chapter has the highest weightage in the board exam, thus scoring well in this chapter will help in scoring in the final paper.
It helps in strengthening concepts of ray optics, improves numerical solving ability, and prepares you for board exams as well as competitive exams like JEE.
Absolutely! The working principles, ray diagrams, and construction of devices like the human eye, microscope, and telescope are explained in detail.
Key topics include reflection, refraction, total internal reflection, lens and mirror formulas, the power of lenses, and optical instruments.
Yes, derivations like the mirror formula, lens formula, and magnification are important for understanding and scoring well in exams.
Questions related to CBSE Class 12th
On Question asked by student community
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your admit card. Some schools may pressure or warn students who fail multiple subjects, but legally they cannot detain you just because of pre-board results if your attendance and internal requirements are completed. In most cases, schools allow students to sit for boards after extra tests, remedial classes, or a written undertaking from parents. So don’t panic—but also don’t be careless. Use this as a wake-up call and seriously work on weak subjects instead of relying on hope alone.
Hello,
You can get the Class 11 English Syllabus 2025-26 from the Careers360 website. This resource also provides details about exam dates, previous year papers, exam paper analysis, exam patterns, preparation tips and many more. you search in this site or you can ask question we will provide you the direct link to your query.
LINK: https://school.careers360.com/boards/cbse/cbse-class-11-english-syllabus
Hello,
No, it’s not true that GSEB (Gujarat Board) students get first preference in college admissions.
Your daughter can continue with CBSE, as all recognized boards CBSE, ICSE, and State Boards (like GSEB) which are equally accepted for college admissions across India.
However, state quota seats in Gujarat colleges (like medical or engineering) may give slight preference to GSEB students for state-level counselling, not for all courses.
So, keep her in CBSE unless she plans to apply only under Gujarat state quota. For national-level exams like JEE or NEET, CBSE is equally valid and widely preferred.
Hope it helps.
Hello,
The Central Board of Secondary Education (CBSE) releases the previous year's question papers for Class 12.
You can download these CBSE Class 12 previous year question papers from this link : CBSE Class 12 previous year question papers (http://CBSE%20Class%2012%20previous%20year%20question%20papers)
Hope it helps !
Hi dear candidate,
On our official website, you can download the class 12th practice question paper for all the commerce subjects (accountancy, economics, business studies and English) in PDF format with solutions as well.
Kindly refer to the link attached below to download:
CBSE Class 12 Accountancy Question Paper 2025
CBSE Class 12 Economics Sample Paper 2025-26 Out! Download 12th Economics SQP and MS PDF
CBSE Class 12 Business Studies Question Paper 2025
CBSE Class 12 English Sample Papers 2025-26 Out – Download PDF, Marking Scheme
BEST REGARDS
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters