NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves
Whenever you use the mobile phone to make a call or when you are watching an X-ray picture in the hospital, you are feeling the power of electromagnetic waves at work. These waves are useful in the modern lives of people, starting with radio waves and how they are used in communications to how they are used in cancer remedies which involve use of gamma rays. This chapter, 8 of Class 12 Physics- Electromagnetic Waves talks about the nature, behavior and practical applications of these invisible energy carriers.
This Story also Contains
- NCERT Exemplar Class 11 Physics Solutions Chapter 8: MCQI
- NCERT Exemplar Class 11 Physics Solutions Chapter 8: MCQII
- NCERT Exemplar Class 11 Physics Solutions Chapter 8: Very Short Answer
- NCERT Exemplar Class 11 Physics Solutions Chapter 8: Short Answer
- NCERT Exemplar Class 11 Physics Solutions Chapter 8: Long Answer
- Main Subtopics of NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves
- NCERT Exemplar Class 12 Physics Solutions Chapter-Wise

NCERT Exemplar Class 12 Physics Solutions Chapter 8 presents a comprehensive and skillfully covered content in order to help students understand this difficult subject. Developed by experienced subject experts of Careers360, these solutions outline complex concepts like the electromagnetic spectrum, wave propagation, displacement current, the correlation between electric and magnetic fields in motion of waves. The resource offers a large range of question types, many answers (multiple-choice questions (MCQs), short answers, long answers, and very long answer questions) used to assist the students in gaining a rounded perception. If you are revising for CBSE board exam or clearing competitive entrance tests such as JEE Main or NEET, this Exemplar solutioncan make a really good company to your revision and concept understanding. Both sets of solutions enhance understanding and confidence: there is plenty of repetitive practice and an opportunity to solve problems with expert help.
Also Read
- NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF
- NCERT Solutions For Class 12 Physics Chapter 8 Electromagnetic Waves
NCERT Exemplar Class 11 Physics Solutions Chapter 8: MCQI
Question:8.1
- microwave region
- visible region
- ultraviolet region
- infrared region
Answer:
The answer is the option (c) ultraviolet regionGiven, energy required to dissociate a carbon monoxide molecule into carbon and oxygen atoms $E=11 \mathrm{eV}$
We know that, $E=h \nu$, where $h=6.62 \times 10^{-34} \mathrm{~J}-\mathrm{s}$
$
\begin{aligned}
v & =\text { frequency } \\
\Rightarrow \quad 11 \mathrm{eV} & =h v \\
v & =\frac{11 \times 1.6 \times 10^{-19}}{h} \mathrm{~J} \\
& =\frac{11 \times 1.6 \times 10^{-19}}{6.62 \times 10^{-34}} \mathrm{~J} \\
& =2.65 \times 10^{15} \mathrm{~Hz}
\end{aligned}
$
This frequency radiation belongs to ultraviolet region.
Question:8.2
A linearly polarized electromagnetic wave given as $E=E_0\hat{i}\cos\left ( kz-\omega t \right )$ is incident normally on a perfectly reflecting infinite wall at z = a. Assuming that the material of the wall is optically inactive, the reflected wave will be given as
(a) $E_r=E_0\hat{i}\cos\left ( kz+\omega t \right )$
(b) $E_r=-E_0\hat{i}\cos\left ( kz-\omega t \right )$
(c) $E_r=-E_0\hat{i}\sin\left ( kz-\omega t \right )$
(d) $E_r=-E_0\hat{i}\cos\left ( kz+\omega t \right )$
Answer:
The answer is the option (a)When a wave is reflected from denser medium, then the type of wave doesn't change but only its phase changes by $180^{\circ}$ or $\pi$ radian.
Thus, for the reflected wave $\hat{\mathbf{z}}=-\hat{\mathbf{z}}, \hat{\mathbf{i}}=-\hat{\mathbf{i}}$ and additional phase of $\pi$ in the incident wave.
Given, here the incident electromagnetic wave is,
$
\mathbf{E}=E_0 \hat{\mathbf{i}} \cos (k z-\omega t)
$
The reflected electromagnetic wave is given by
$
\begin{aligned}
\mathbf{E}_r & =E_0(-\hat{\mathbf{i}}) \cos [k(-z)-\omega t+\pi] \\
& =-E_0 \hat{\mathbf{i}} \cos [-(k z+\omega t)+\pi] \\
& =E_0 \hat{\mathbf{i}} \cos \left[-\left(k_z+\omega t\right)=E_0 \hat{\mathbf{i}} \cos (k z+\omega t)\right]
\end{aligned}
$
Question:8.3
Light with an energy flux of 20 wb/cm2 falls on a non-reflecting surface at normal incidence. If the surface has an area of 30 cm2, the total momentum delivered for 30 minutes is
A. 108 × 104 kg m/s
B. 36 × 10-5 kg m/s
C. 1.08 × 107 kg m/s
D. 36 × 10-4 kg m/s
Answer: The answer is the option (d) $36 \times 10^{-4} kg m/s$
Given, energy flux $\phi=20 \mathrm{~W} / \mathrm{cm}^2$
Area, $\quad A=30 \mathrm{~cm}^2$
Time, $t=30 \mathrm{~min}=30 \times 60 \mathrm{~s}$
Now, total energy falling on the surface in timet is, $U=\phi A t=20 \times 30 \times(30 \times 60) \mathrm{J}$
Momentum of the incident light $=\frac{U}{\mathrm{C}}$
$
=\frac{20 \times 30 \times(30 \times 60)}{3 \times 10^8} \Rightarrow=36 \times 10^{-4} \mathrm{~kg}-\mathrm{ms}^{-1}
$
Momentum of the reflected light $=0$
$\therefore$ Momentum delivered to the surface
$
=36 \times 10^{-4}-0=36 \times 10^{-4} \mathrm{~kg}-\mathrm{ms}^{-1}
$
Question:8.4
The electric field intensity produced by the radiations coming from 100 W bulb at a 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is
A. $E/2$
B. $E/\sqrt{2}$
C. $\sqrt{2}/E$
D. $2E$
Answer:
The answer is the option (b) $E/\sqrt{2}$
We know that, $\quad E_0 \propto \sqrt{P_{a v}}$
$
\begin{array}{ll}
\therefore & \frac{\left(E_o\right)_1}{\left(E_o\right)_2}=\sqrt{\frac{\left(P_{\mathrm{av}}\right)_1}{\left(P_{\mathrm{av}}\right)_2}} \Rightarrow \frac{E}{\left(E_o\right)_2}=\sqrt{\frac{1000}{50}} \\
& \left(E_o\right)_2=E / \sqrt{2}
\end{array}
$
Now according to question, $P^{\prime}=50 \mathrm{~W}, P=100 \mathrm{~W}$
$\therefore$ Putting these value in Eq. (i), we get
$
\frac{E^{\prime}}{E}=\frac{50}{100} \Rightarrow \frac{E^{\prime}}{E}=\frac{1}{2} \Rightarrow E^{\prime}=\frac{E}{2}
$
Question:8.5
If E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of the electromagnetic wave is along
a. $E$
b. $B$
c. $E \times B$
d. $B \times E$
Answer: The answer is the option (c) $E \times B$
The direction of propagation of electromagnetic wave is perpendicular to both electric field vector $\mathbf{E}$ and magnetic field vector $\mathbf{B}$, i.e., in the direction of $\mathbf{E} \times \mathbf{B}$.
This can be seen by the diagram given below
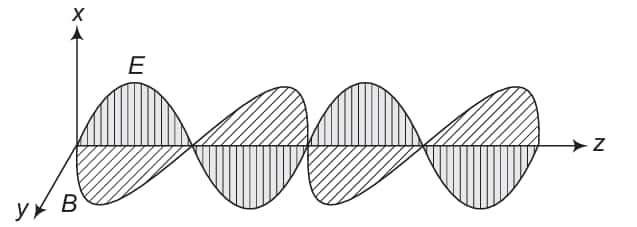
Here, electromagnetic wave is along the $z$-direction which is given by the cross product of $\mathbf{E}$ and $\mathbf{B}$.
Question:8.6
The ratio of contributions made by the electric field and magnetic field components to the intensity of an EM wave is
a. $c:1$
b. $\sqrt{c}:1$
c. $c^{2}:1$
d. $1:1$
Answer:
The answer is the option (d) 1: 1
Intensity in terms of electric field $\quad U_{\mathrm{av}}=\frac{1}{2} \varepsilon_0 E_0^2$
Intensity in terms of magnetic field $U_{\mathrm{av}}=\frac{1}{2} \frac{B_0^2}{\mu_0}$
Now taking the intensity in terms of electric field.
$
\begin{aligned}
& \qquad \begin{aligned}
\left(U_{\text {av }}\right) \text { electric field } & =\frac{1}{2} \varepsilon_0 E_0^2 \\
& =\frac{1}{2} \varepsilon_0\left(c B_0\right)^2 \\
& =\frac{1}{2} \varepsilon_0 \times c^2 B^2 \\
\text { But, } \quad c & =\frac{1}{\sqrt{\mu_0 \varepsilon_0}} \\
\therefore \quad\left(U_{\text {av }}\right)_{\text {Electric field }} & =\frac{1}{2} \varepsilon_0 \times \frac{1}{\mu_0 \varepsilon_0} B_0^2=\frac{1}{2} \frac{B_0^2}{\mu_0} \\
& =\left(U_{\text {av }}\right)_{\text {magnetic field }}
\end{aligned}
\end{aligned}
$
Thus, the energy in electromagnetic wave is divided equally between electric field vector and magnetic field vector.
Therefore, the ratio of contributions by the electric field and magnetic field components to the intensity of an electromagnetic wave is $1: 1$.
Question:8.7
An EM wave radiates outwards from a dipole antenna, with $E_{o}$ as the amplitude of its electric field vector. The electric field Eo which transports significant energy from the source falls off as
a. $\frac{1}{r^{3}}$
b. $\frac{1}{r}$
c. $\frac{1}{r^{2}}$
d. remains constant
Answer:
A diode antenna radiates the electromagnetic waves outwards. The amplitude of electric field vector falls intensity inversely as the distance (r) from the antenna
The answer is the option (b) 1/r
NCERT Exemplar Class 11 Physics Solutions Chapter 8: MCQII
Question:8
An electromagnetic wave travels in vacuum along z-direction:
$E=\left ( E_1\hat{i}+E_2\hat{j} \right ) \cos \left ( kz-\omega t \right )$.
Choose the correct options from the following:
a) the associated magnetic field is given as $B=\frac{1}{c}\left ( E_1\hat{i}+E_2\hat{j} \right ) \cos \left ( kz-\omega t \right )$
b) the associated magnetic field is given as $B=\frac{1}{c}\left ( E_1\hat{i}-E_2\hat{j} \right ) \cos \left ( kz-\omega t \right )$
c) the given electromagnetic waves is plane polarised
d) the given electromagnetic field is circularly polarised
Answer:
The correct answers are the options a), and c).
In electromagnetic wave, the electric field vector is given as,
$
E=\left(E_1 \hat{i}+E_2 \hat{j}\right) \cos (k z-\omega t)
$
In electromagnetic wave, the associated magnetic field vector,
$
B=\frac{E}{c}=\frac{\left(E_1 \hat{i}+E_2 \hat{j}\right)}{c} \cos (k z-\omega t)
$
As $E$ and $B$ are perpendicular to each other and the propagation of electromagnetic wave is perpendicular to $E$ as well as $B$, so the given electromagnetic wave is plane polarised.
Question:8.9
An electromagnetic wave travelling along $z$-axis is given as: $\mathbf{E}=\mathbf{E}_0 \cos (k z-\omega t$.$) . \text{Choose the correct options from the following;}$
(a) The associated magnetic field is given as $\mathbf{B}=\frac{1}{c} \hat{\mathbf{k}} \times \mathbf{E}=\frac{1}{\omega}(\hat{\mathbf{k}} \times \mathbf{E})$.
(b) The electromagnetic field can be written in terms of the associated magnetic field as $\mathbf{E}=c(\mathbf{B} \times \hat{\mathbf{k}})$.
(c) $\hat{\mathbf{k}} \cdot \mathbf{E}=0, \hat{\mathbf{k}} \cdot \mathbf{B}=0$.
(d) $\hat{\mathbf{k}} \times \mathbf{E}=0, \hat{\mathbf{k}} \times \mathbf{B}=0$.
Answer: The correct answers are the options (a, b and c)
Suppose an electromagnetic wave is travelling along negative $z$-direction. Its electric field is given by
$
\mathrm{E}=E_0 \cos (k z-\omega t)
$
which is perpendicular to $z$-axis. It acts along negative $y$-direction.
The associated magnetic field $\mathbf{B}$ in electromagnetic wave is along $x$-axis i.e., along $\hat{\mathbf{k}} \times \mathbf{E}$.
As,
$
\begin{aligned}
& B_o=\frac{E_o}{c} \\
& \mathbf{B}=\frac{1}{c}(\hat{\mathbf{k}} \times \mathbf{E})
\end{aligned}
$
The associated electric field can be written in terms of magnetic field as
$
\mathbf{E}=c(\mathbf{B} \times \hat{\mathbf{k}})
$
Angle between $\hat{\mathbf{k}}$ and $\mathbf{E}$ is $90^{\circ}$ between $\hat{\mathbf{k}}$ and $\mathbf{B}$ is $90^{\circ}$. Therefore, $\mathbf{E}=1 E \cos 90^{\circ}=0$ and $\hat{\mathbf{k}} \cdot \mathbf{B}=1 E \cos 90^{\circ}=0$.
Question:8.10
A plane electromagnetic wave propagating along x-direction can have the following pairs of E and B
a) Bx, Ey
b) Ex, By
c) Ey, Bz
d) Ez, By
Answer: The correct answers are the options,
c) Ey, Bzd) Ez, By
As electric and magnetic field vectors $\mathbf{E}$ and $\mathbf{B}$ are perpendicular to each other as well as perpendicular to the direction of propagation of electromagnetic wave.
Here in the question electromagnetic wave is propagating along $x$-direction. So, electric and magnetic field vectors should have either $y$-direction or $z$-direction.
Question:8.11
A charged particle oscillates about its mean equilibrium position with a frequency of 109 Hz. The electromagnetic waves produced:
a) fall in the region of radio waves
b) will have a wavelength of 0.3 m
c) will have a frequency of 109 Hz
d) will have a frequency of 2 × 109 Hz
Answer: The correct answers are the options,
a. fall in the region of radio waves
b. will have a wavelength of 0.3 m
c. will have a frequency of 109 Hz
Given, frequency by which the charged particles oscillates about its mean equilibrium position $=10^9 \mathrm{~Hz}$.
So, frequency of electromagnetic waves produced by the charged particle is $v=10^9 \mathrm{~Hz}$.
Wavelength $\lambda=\frac{c}{v}=\frac{3 \times 10^8}{10^9}=0.3 \mathrm{~m}$
Also, frequency of $10^9 \mathrm{~Hz}$ fall in the region of radiowaves.
Question:8.12
The source of electromagnetic waves can be a charge
a) at rest
b) moving with a constant velocity
c) falling in an electric field
d) moving in a circular orbit
Answer: The correct answers are the options,
c) falling in an electric field
d) moving in a circular orbit
In circular motion, the direction of the motion of charge is changing continuously, thus it is an accelerated motion and this option is correct.
Also, we know that a charge starts accelerating when it falls in an electric field.
Question:8.13
An EM wave of intensity I falls on a surface kept in vacuum and exerts radiation pressure p on it. Which of the following are true?
a) radiation pressure is I/c if the wave is totally reflected
b) radiation pressure is I/c if the wave is totally absorbed
c) radiation pressure is in the range I/c < p < 2I/c for real surface
d) radiation pressure is 2I/c if the wave is totally reflected
Answer: The correct answers are the options,
a) radiation pressure is I/c if the wave is totally absorbed
c) radiation pressure is in the range I/c < p < 2I/c for real surface
d) radiation pressure is 2I/c if the wave is totally reflected
Radiation pressure $(p)$ is the force exerted by electromagnetic wave on unit area of the surface, i.e., rate of change of momentum per unit area of the surface.
Momentum per unit time per unit area
$
=\frac{\text { Intensity }}{\text { Speed of wave }}=\frac{I}{C}
$
Change in momentum per unit time per unit area $=\frac{\Delta I}{C}=$ radiation pressure $(p)$
i.e.,
$
p=\frac{\Delta I}{c}
$
Momentum of incident wave per unit time per unit area $=\frac{I}{C}$
When wave is fully absorbed by the surface, the momentum of the reflected wave per unit time per unit area $=0$.
Radiation pressure $(p)=$ change in momentum per unit time per unit area $=\frac{\Delta I}{c}=\frac{I}{c}-0=\frac{I}{c}$.
When wave is totally reflected, then momentum of the reflected wave per unit time per unit area $=-\frac{I}{\mathrm{C}}$, Radiation pressure $p=\frac{I}{\mathrm{C}}-\left(-\frac{I}{\mathrm{C}}\right)=\frac{2 I}{\mathrm{C}}$.
Here, $p$ lies between $\frac{I}{c}$ and $\frac{2 I}{c}$.
NCERT Exemplar Class 11 Physics Solutions Chapter 8: Very Short Answer
Question:8.14
Why is the orientation of the portable radio with respect to broadcasting stations important?
Answer:
We know that the electromagnetic waves are plane-polarized. Therefore, the antennas are to be placed in parallel to the vibration of the electric or magnetic field of the wave. That is why the orientation of the portable radio with respect to the broadcasting station is important.Question:8.15
Why does a microwave oven heat up a food item containing water molecules most efficiently?
Answer:
The frequency of the microwave is exactly the same as that of the resonant frequency of the water molecules in a food item. That is why, the microwave oven heats up a food item containing water molecules most efficiently.Question:8.16
Answer:
The displacement current through the capacitor is,
Here,
$
I_d=I_c=\frac{d q}{d t}
$
Putting this value in Eq (i), we get
$
\begin{aligned}
& I_d=I_c=-q_0 \sin 2 \pi v t \times 2 \pi v \\
& I_d=I_c=-2 \pi v q_0 \sin 2 \pi v t
\end{aligned}
$
Question:8.17
Answer:
Capacitive reactance,
$X_c= \frac{1}{2} \pi fc$
As the frequency is decreasing, therefore capacitive reactance $(X_c)$ will increase with time and the current that is flowing through will become inversely proportional to $X_c$.
Question:8.18
Answer:
Magnetic field $\mathbf{B}=B_0 \sin \omega t$
Given, equation $B=12 \times 10^{-8} \sin \left(1.20 \times 10^7 z-3.60 \times 10^{15} t\right) \mathrm{T}$.
On comparing this equation with standard equation, we get
$
B_0=12 \times 10^{-8}
$
The average intensity of the beam
$
\begin{aligned}
I_{\mathrm{av}} & =\frac{1}{2} \frac{B_0^2}{\mu_0} \cdot C=\frac{1}{2} \times \frac{\left(12 \times 10^{-8}\right)^2 \times 3 \times 10^8}{4 \pi \times 10^{-7}} \\
& =1.71 \mathrm{~W} / \mathrm{m}^2
\end{aligned}
$
Question:8.19
Answer:
In an electromagnetic waves, Let $\vec{E}$ be varying along y-axis, $\vec{B}$ is along z- axis and propagation of wave be along x-axis. Then $\vec{E} \times \vec{B}$ will tell the direction of propagation of energy flow in electromagnetic wave, along x-axis.
Let
$\\ \vec{E} =E_0 \sin\left ( \omega t -kx \right )\hat{j}\\$
$\vec{B} =B_0 \sin\left ( \omega t -kx \right )\hat{k}\\ $
$S=\frac{1}{\mu_0}\left ( \vec{E} \times \vec{B} \right )=\frac{1}{\mu_0}\;E_0B_0\sin^{2}\left ( \omega t- kx\right )\left ( \hat{j}\times \hat{k} \right )\\$
$\Rightarrow S=\frac{E_0B_0}{\mu_0}\sin^{2}\left ( \omega t-kx \right )\hat{i}\; \; \; \; \; \;$
Since $\sin^{2}\left ( \omega t-kx \right )$ is never negative, $\vec{S}\left ( x,t \right )$ always point in the positive X-direction, i.e, in the direction of wave propagation.
The variation of $\left | S \right |$ with time T will be as given in the figure below:

Question:8.20
Answer:
Like other waves, the electromagnetic wave has the same properties. Therefore, an electromagnetic wave has energy and momentum. It exerts pressure called radiation pressure due to momentum.NCERT Exemplar Class 11 Physics Solutions Chapter 8: Short Answer
Question:8.21
Answer:
Consider the figure ginen below to prove that the magneti field B at a point in between the plater of a paravel- plate copocior during charging is $\frac{\varepsilon_0 \mu_0 r}{2} \frac{d E}{d t}$
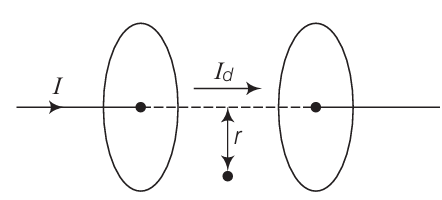
Let $I_d$ be the displacement current in the region between two plates of parallel plate capacitor, in the figure.
The magnetic field induction at a point in a region between two plates of capacitor at a perpendicular distance $r$ from the axis of plates is
$
\begin{array}{rlr}
B & =\frac{\mu_0 2 I_d}{4 \pi r}=\frac{\mu_0}{2 \pi r} I_d=\frac{\mu_0}{2 \pi r} \times \varepsilon_0 \frac{d \phi_E}{d t} & {\left[\because I_d=\frac{E_0 d \phi_E}{d t}\right]} \\
& =\frac{\mu_0 \varepsilon_0}{2 \pi r} \frac{d}{d t}\left(E \pi r^2\right)=\frac{\mu_0 \varepsilon_0}{2 \pi r} \pi r^2 \frac{d E}{d t} & {\left[\because \phi_E=E \pi r^2\right]} \\
B & =\frac{\mu_0 \varepsilon_0 r}{2} \frac{d E}{d t} &
\end{array}
$
Question:8.22
Electromagnetic waves with wavelength
i) $\lambda _{1}$ is used in satellite communication
ii) $\lambda _{2}$ is used to kill germs in water purifies
iii) $\lambda _{3}$ is used to detect leakage of oil in underground pipelines
iv) $\lambda _{4}$ is used to improve visibility in runaways during fog and mist conditions
a) identify and name the part of the electromagnetic spectrum to which these radiations belong
b) arrange these wavelengths in ascending order of their magnitude
c) write one more application of each
Answer:
a)
i) $\lambda _{1}$ is used in satellite communication : a microwave
ii) $\lambda _{2}$ is used to kill germs in water purifier for killing germs : a UV ray
iii) $\lambda _{3}$ is used in improving the visibility: a X-ray
iv) $\lambda _{4}$ is used to improve visibility in runaways during fog and mist conditions: an infrared ray
b) By arranging those wavelengths in ascending order: $\lambda _{3}<\lambda _{2}<\lambda _{4}<\lambda _{1}$
c)
i) Gamma rays: Those are used in nuclear structures.
ii) X rays: Those are used in medical diagnosis.
iii) UV rays: Those are used in the preservation of food.
iv) Infrared rays: Those are used to take photograph
Question:8.23
Show that the average value of radiant flux density S over a single period T is given by
$S= \frac{(\frac{1}{2}c\mu _{0})}{E{_{0}}^{2}}$
Answer:
Radiant flux density $S=\frac{1}{\mu_0}(\mathbf{E} \times \mathbf{B})=c^2 \varepsilon_0(\mathbf{E} \times \mathbf{B})$ $
\left[\because c=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\right]
$
Suppose electromagnetic waves be propagating along $x$-axis. The electric field vector of electromagnetic wave be along $y$-axis and magnetic field vector be along $z$-axis. Therefore,
and
$
\begin{aligned}
\mathbf{E}_0 & =\mathbf{E}_0 \cos (k x-\omega t) \\
\mathbf{B} & =\mathbf{B}_0 \cos (k x-\omega t) \\
\mathbf{E} \times \mathbf{B} & =\left(\mathbf{E}_0 \times \mathbf{B}_0\right) \cos ^2(k x-\omega t) \\
\mathbf{S} & =\mathbf{c}^2 \varepsilon_0(\mathbf{E} \times \mathbf{B}) \\
& =c^2 \varepsilon_0\left(\mathbf{E}_0 \times \mathbf{B}_0\right) \cos ^2(k x-\omega t)
\end{aligned}
$
Average value of the magnitude of radiant flux density over complete cycle is
$
\begin{aligned}
S_{\mathrm{av}} & =c^2 \varepsilon_0\left|\mathbf{E}_0 \times \mathbf{B}_0\right| \frac{1}{T} \int_0^T \cos ^2(k x-\omega t) d t \\
& =c^2 \varepsilon_0 E_0 B_0 \times \frac{1}{T} \times \frac{T}{2} \ \ \ \ {\left[\because \int_0^T \cos ^2(k x-\omega t) d t=\frac{T}{2}\right]} \\
\Rightarrow \quad S_{\mathrm{av}} & =\frac{c^2}{2} \varepsilon_0 E_0\left(\frac{E_0}{c}\right) \ \ {\left[\text { As, } c=\frac{E_0}{B_0}\right]}\\
& =\frac{c}{2} \varepsilon_0 E_0^2=\frac{c}{2} \times \frac{1}{c^2 \mu_0} E_0^2 \ \ \ {\left[c=\frac{1}{\sqrt{\mu_0 \varepsilon_0}} \text { or } \varepsilon_0=\frac{1}{c^2 \mu_0}\right]} \\
\Rightarrow \quad S_{\mathrm{av}} & =\frac{E_0^2}{2 \mu_0 c}
\end{aligned}
$
Hence proved.
Question:8.24
Answer:
The capacitor has a capacitance of $C=2\mu F$Displacement current $I_{d}=1\; mA$
Charge in the capacitor,
$q=CV$
or, $I_{d}dt =C\; dV \; \; \; \; \; \; \; \; \; \left [ as,q=it \right ]$
or, $I_{d} =C\; \frac{dV}{dt}$
or, $\frac{dV}{dt}= \frac{(1\times10^{-3})}{(2\times10^{-6})}$
or, $\frac{dV}{dt}= 500\frac{V}{s}$
Therefore, by applying a voltage of $500\frac{V}{s}$, we will get the mentioned displacement current.
Question:8.25
Answer:
Energy received by the surface per second, $E = IA$No.of photons received per second by the surface
$=N=\frac{E}{E_{photon}}=\frac{E\lambda }{hc}=\frac{IA\lambda }{hc}$
For a perfectly absorbing surface, is
$\Delta P=\frac{h}{\lambda }$
Force, $F=N.\Delta P=\left ( \frac{IA\lambda }{hc} \right )\left ( \frac{h}{\lambda } \right )=\left ( \frac{IA}{c} \right )$
Pressure,
$P=\frac{F}{A}=\frac{I}{c}$
Question:8.26
Answer:
When the distance is doubled, the intensity of light becomes one-fourth.Following are the geometrical characteristics of the LASER those missing in the case of normal light from the bulb:
a) unidirectional
b) monochromatic
c) coherent light
The above characteristics are missing in the case of light from the bulb
Question:8.27
Answer:
Even though an electric field E exerts a force qE on a charged particle yet the electric field of an EM wave does not contribute to the radiation pressure because radiation pressure is the result of the action of the magnetic field of the wave on the electric currents which is induced by the electric field.NCERT Exemplar Class 11 Physics Solutions Chapter 8: Long Answer
Question:8.28
Answer:
$\begin{aligned} \mathbf{E} & =\frac{\lambda \hat{\mathbf{e}}_s}{2 \pi \varepsilon_0 a} \hat{\mathbf{j}} \\ \mathbf{B} & =\frac{\mu_0 \mathrm{i}}{2 \pi a} \hat{\mathbf{i}}=\frac{\mu_0 \lambda v}{2 \pi a} \hat{\mathbf{i}} \\ \mathbf{S} & =\frac{1}{\mu_0}[\mathbf{E} \times \mathbf{B}]=\frac{1}{\mu_0}\left[\frac{\lambda_{\hat{\mathbf{j}}}}{2 \pi \varepsilon_0 a} \times \frac{\mu_0}{2 \pi a} \lambda \sqrt{\hat{\mathbf{i}}}\right] \\ & =\frac{\lambda^2 v}{4 \pi^2 \varepsilon_0 a^2}(\hat{\mathbf{j}} \times \hat{\mathbf{i}})=-\frac{\lambda^2 v}{4 \pi^2 \varepsilon_0 a^2} \hat{\mathbf{k}}\end{aligned}$Question:8.29
Answer:
Suppose distance between the parallel plates is $d$ and applied voltage $V(t)=V_o2\pi vt$ Thus, electric field
$
\begin{array}{ll}
\text { Now using Ohm's law, } & \begin{aligned}
E & =\frac{V_0}{d} \sin (2 \pi v t) \\
J_c & =\frac{1}{\rho} \frac{V_0}{d} \sin (2 \pi v t) \\
\Rightarrow &
\end{aligned}=\frac{V_0}{\rho d} \sin (2 \pi v t)=J_0^c \sin 2 \pi v t \\
\text { Here, } & J_0^c=\frac{V_0}{\rho d}
\end{array}
$
Now the displacement current density is given as
$
\begin{aligned}
J_d & =\varepsilon \frac{\delta E}{d t}=\frac{\varepsilon \delta}{d t} \\
& =\frac{\varepsilon 2 \pi V V_0}{d} \cos (2 \pi V t) \\
& =J_0^d \cos (2 \pi V t) \\
\text { where, } \quad & \quad J_0^d=\frac{2 \pi V \varepsilon V_0}{d} \\
\Rightarrow \quad \frac{J_0^d}{J_0^c} & =\frac{2 \pi V \varepsilon V_0}{d} \cdot \frac{\rho d}{V_0}=2 \pi v \varepsilon \rho \\
& =2 \pi \times 80 \varepsilon_0 V \times 0.25=4 \pi \varepsilon_0 V \times 10 \\
& =\frac{10 \mathrm{~V}}{9 \times 10^9}=\frac{4}{9}
\end{aligned}
$
Question:8.30
A long straight cable of length l is placed symmetrically along the z-axis and has radius a. The cable consists of a thin wire and a coaxial conducting tube. An alternating current $I(t)=I_{0}\; \sin \left ( 2\pi vt \right )$ flows down the central thin wire and returns along the coaxial conducting tube. The induced electric field at a distance s from the wire inside the cable is $E(s,t)=\mu _{0}I_{0}v\; coz\; \left ( 2\pi vt \right ).$In $\left ( \frac{s}{a} \right )\hat{k}$
a) calculate the displacement current density inside the cable
b) integrate the displacement current density across the cross-section of the cable to find the total displacement current I
c) compare the conduction current $I_{o}$ with the displacement current $I_{o}d$
Answer:
(a) Given, the induced electric field at a distance $r$ from the wire inside the cable is
$
\mathbf{E}(s, t)=\mu_0 I_0 v \cos (2 \pi v t) \ln \left(\frac{s}{a}\right) \hat{\mathbf{k}}
$
Now, displacement current density,
$
\mathbf{J}_d=\varepsilon_0 \frac{d \mathbf{E}}{d t}=\varepsilon_0 \frac{d}{d t}\left[\mu_0 I_0 v \cos (2 \pi v t) \ln \left(\frac{s}{a}\right) \hat{\mathbf{k}}\right]
$
$\begin{aligned} & =\varepsilon_0 \mu_0 I_0 v \frac{d}{d t}[\cos 2 \pi v t] \ln \left(\frac{s}{a}\right) \hat{\mathbf{k}} \\ & =\frac{1}{c^2} I_0 v^2 2 \pi[-\sin 2 \pi v t] \ln \left(\frac{s}{a}\right) \hat{\mathbf{k}} \\ & =\frac{v^2}{c^2} 2 \pi I_0 \sin 2 \pi v t \ln \left(\frac{a}{s}\right) \hat{\mathbf{k}} \\ & =\frac{1}{\lambda^2} 2 \pi I_0 \ln \left(\frac{a}{s}\right) \sin 2 \pi v t \hat{\mathbf{k}} \\ & =\frac{2 \pi I_0}{\lambda_2} \ln \frac{a}{s} \sin 2 \pi v t \hat{\mathbf{k}}\end{aligned}$
(b)
$\begin{aligned} I_d & =\int J_d s d s d \theta=\int_{s=0}^a J_d s d s \int_0^{2 \pi} d \theta=\int_{s=0}^a J_d s d s \times 2 \pi \\ & =\int_{s=0}^a\left[\frac{2 \pi}{\lambda^2} I_0 \log _e\left(\frac{a}{s}\right) s d s \sin 2 \pi v t\right] \times 2 \pi \\ & =\left(\frac{2 \pi}{\lambda}\right)^2 I_0 \int_{s=0}^a\left(\frac{a}{s}\right) s d s \sin 2 \pi v t \\ & =\left(\frac{2 \pi}{\lambda}\right)^2 I_0 \int_{s=0}^a \ln \left(\frac{a}{s}\right) \frac{1}{2} d\left(s^2\right) \cdot \sin 2 \pi v t \\ & =\frac{a^2}{2}\left(\frac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \int_{s=0}^a \ln \left(\frac{a}{s}\right) \cdot d\left(\frac{s}{a}\right)^2 \\ & =\frac{a^2}{4}\left(\frac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \int_{s=0}^a \ln \left(\frac{a}{s}\right)^2 \cdot d\left(\frac{s}{a}\right)^2 \\ & =-\frac{a^2}{4}\left(\frac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \int_{s=0}^a \ln \left(\frac{s}{a}\right)^2 \cdot d\left(\frac{s}{a}\right)^2\end{aligned}$
$\begin{aligned} & =-\frac{a^2}{4}\left(\frac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \times(-1) \\ \therefore & I_d =\frac{a^2}{4}\left(\frac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t =\left(\frac{2 \pi a}{2 \lambda}\right)^2 I_0 \sin 2 \pi v t\end{aligned}$
(c)
The displacement current,
$
\begin{aligned}
I_d =\left(\frac{2 \pi a}{2 \lambda}\right)^2 I_0 \sin 2 \pi v t=I_{0 d} \sin 2 \pi v t \\
\text { Here, } I_{0 d} =\left(\frac{2 \pi a}{2 \lambda}\right)^2 I_0=\left(\frac{a \pi}{\lambda}\right)^2 I_0 \\
\therefore \frac{I_{0 d}}{I_0} =\left(\frac{a \pi}{\lambda}\right)^2
\end{aligned}
$
Question:8.31
A plane EM wave travelling in vacuum along z-direction is given by
$E=E_{0}\sin (kz-\omega t)\hat{i}\; and \; B=B_{0}\sin (kz-\omega t)\hat{j}$
a) evaluate $\oint E.dl$ over the rectangular loop 1234 shown in the figure
b) evaluate $\int B.ds$ over the surface bounded by loop 1234
c) use equation $\oint E.dl=\frac{-d\phi _{B}}{dt}$ to prove $\frac{E_{0}}{B_{0}}=c$
d) by using a similar process and the equation
$\oint B.dl=\mu _{0}I\epsilon _{0}\frac{-d\phi _{E}}{dt}$ prove that $c=\frac{1}{\sqrt{\mu _{0}\epsilon _{0}}}$
Answer:
a)
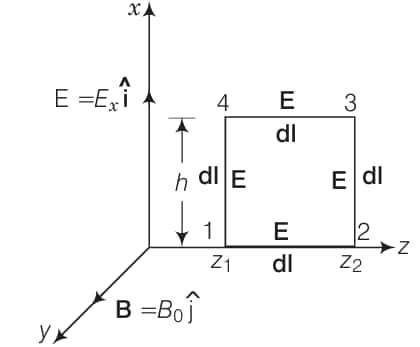
During the propagation of electromagnetic wave a long $z$-axis, let electric field vector (E) be along $x$-axis and magnetic field vector $\mathbf{B}$ along $y$-axis, i.e., $\mathbf{E}=E_0 \hat{\mathbf{i}}$ and $\mathbf{B}=B_0 \hat{\mathbf{j}}$.
Line integral of $E$ over the closed rectangular path 1234 in $x$ - $z$ plane of the figure
$
\begin{aligned}
\oint \mathbf{E} \cdot \mathbf{d} \mathbf{l} & =\int_1^2 \mathbf{E} \cdot \mathbf{d} \mathbf{l}+\int_2^3 \mathbf{E} \cdot \mathbf{d} \mathbf{l}+\int_3^4 \mathbf{E} \cdot \mathbf{d} \mathbf{l}+\int_4^1 \mathbf{E} \cdot \mathbf{d} \mathbf{l} \\
& =\int_1^2 \mathbf{E} \cdot \mathbf{d} \operatorname{los} 90+\int_2^3 \mathbf{E} \cdot \mathbf{d} \operatorname{lcos} 0+\int_3^4 \mathbf{E} \cdot \mathbf{d} \operatorname{lcos} 90+\int_4^1 \mathbf{E} \cdot \mathbf{d} \operatorname{lcos} 180^{\circ} \\
& =E_0 h\left[\sin \left(k z_2-\omega t\right)-\sin \left(k z_1-g \omega t\right)\right]
\end{aligned}
$
b)
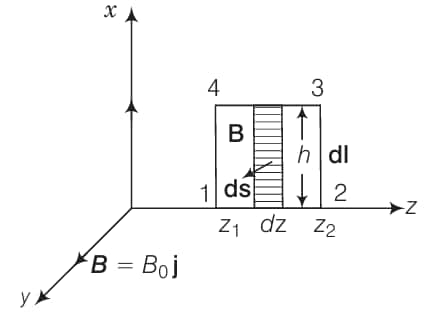
For evaluating $\int \mathbf{B} \cdot \mathbf{d s}$, let us consider the rectangle 1234 to be made of strips of are $d s=h d z$ each.
$
\begin{aligned}
\int \mathbf{B} \cdot \mathbf{d s}=\int \mathbf{B} \cdot \mathbf{d s} \cos 0 & =\int \mathbf{B} \cdot \mathbf{d s}=\int_{Z_1}^{Z_2} B_0 \sin (k z-\omega t) h d z \\
& =\frac{-B_0 h}{k}\left[\cos \left(k z_2-\omega t\right)-\cos \left(k z_1-\omega t\right)\right]
\end{aligned}
$
c)
Given, $\oint \mathbf{E} \cdot \mathbf{d l}=\frac{-d \phi_B}{d t}=-\frac{d}{d t} \oint \mathbf{B} \cdot \mathbf{d s}$
Putting the values from Eqs. (i) and (ii), we get
$
\begin{array}{ll}
& E_0 h\left[\sin \left(k z_2-\omega t\right)-\sin \left(k z_1-\omega t\right)\right] \\
= & \frac{-d}{d t}\left[\frac{B_y h}{k}\left\{\cos \left(k z_2-\omega t\right)-\cos \left(k z_1-\omega t\right)\right]\right. \\
= & \frac{B_y h}{k} \omega\left[\sin \left(k z_2-\omega t\right)-\sin \left(k z_1-\omega t\right)\right] \\
\Rightarrow & E_0=\frac{B_0 \omega}{k}=B_y c \\
\Rightarrow & \frac{E_0}{B_0}=c
\end{array}
$
d)
For evaluating $\oint \mathbf{B} \cdot \mathbf{d l}$, let us consider a loop 1234 in $y-z$ plane as shown in figure given below
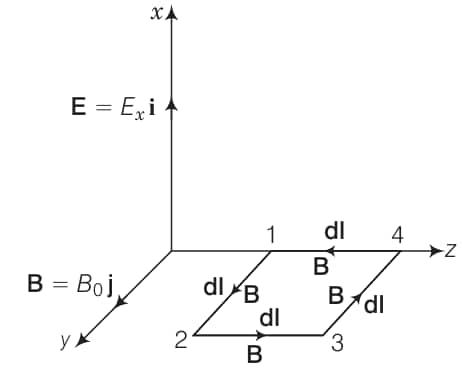
$
\begin{aligned}
\oint \mathbf{B} \cdot \mathbf{d l} & =\int_1^2 \mathbf{B} \cdot \mathbf{d l}+\int_2^3 \mathbf{B} \cdot \mathbf{d l}+\int_3^4 \mathbf{B} \cdot \mathbf{d l}+\int_4^1 \mathbf{B} \cdot \mathbf{d l} \\
& =\int_1^2 \mathbf{B} \cdot \mathbf{d l} \cos 0+\int_2^3 \mathbf{B} \cdot \mathbf{d l} \cos 90^{\circ}+\int_3^4 \mathbf{B} \cdot \mathbf{d l} \cos 180^{\circ}+\int_4^1 \mathbf{B} \cdot \mathbf{d l} \cos 90^{\circ} \\
& =B_0 h\left[\sin \left(k z_1-\omega t\right)-\sin \left(k z_2-\omega t\right)\right.
\end{aligned}
$
Question:8.32
A plane EM wave travelling along z-direction is described by $E=E_{0}\sin (kz-\omega t)\hat{i}\; and\; B=B_{0}\sin (kz-\omega t)\hat{j}$ show that,
i) the average energy density of the wave is given by
$u_{av}=\frac{(u_{E}+u_{B})}{2}=\frac{1}{4}.\varepsilon _{0}E^{2}+\frac{1}{4}.\frac{B^{2}}{\mu _{0}}$
ii) the time - averaged intensity of the wave is given by
$I_{av}=u_{av}c=\frac{1}{2} (\varepsilon _{0}E^{2})c$
Answer:
i) The energy density due to electric field E is$u_{\varepsilon }=\frac{1}{2}(\varepsilon _{0}E^{2})$
The energy density due to magnetic field B is
$u_{B}=\frac{1}{2}\left ( \frac{B^{2}}{\mu _{0}} \right )$
The average energy density of the wave is given by :
$u_{av}=\frac{\left ( u_{E}+u_{B} \right )}{2}=\frac{1}{4}.\varepsilon _{0}E^{2}+\frac{1}{4}.\frac{B^{2}}{\mu _{0}}$
ii) $u_{av}=\frac{\left ( u_{E}+u_{B} \right )}{2}=\frac{1}{4}.\varepsilon _{0}E^{2}+\frac{1}{4}.\frac{B^{2}}{\mu _{0}}$
Assuming $u_{E}=u_{B},$
$u_{av}=\frac{1}{2}\left ( \varepsilon _{0}E^{2} \right )=\frac{1}{2}\left ( \frac{B^{2}}{\mu _{0}} \right )$
We know that $c=\frac{1}{\sqrt{\mu _{0}\varepsilon _{0}}}=\left ( \frac{E_{0}}{B_{0}} \right )$
The time -averaged intensity of the wave is given as
$I_{av}=u_{av}c=\frac{1}{2}\left ( \varepsilon _{0}E^{2} \right )c$
Main Subtopics of NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves
- Introduction
- Displacement Current
- Electromagnetic Waves
- Sources of electromagnetic waves
- Nature Of Electromagnetic Waves
- Energy Density And Intensity Of EM Waves
- Electromagnetic Spectrum
- Radio waves
- Microwaves
- Infrared waves
- Visible rays
- Ultraviolet rays
- X-rays
- Gamma rays
NCERT Exemplar Class 12 Physics Solutions Chapter-Wise
|
Chapter 8 Electromagnetic Waves |
NCERT Exemplar Class 12 Solutions
- NCERT Exemplar Class for 12 Physics
- NCERT Exemplar Class 12 Chemistry Solutions
- NCERT Exemplar Class 12 Mathematics Solutions
- NCERT Exemplar Class 12 Biology Solutions
Check Class 12 Physics Chapter-wise Solutions
Also, Read NCERT Solution subject-wise
- NCERT Solution for Class 12 Physics
- NCERT Solution for Class 12 Chemistry
- NCERT Solution for Class 12 Maths
- NCERT Solution for Class 12 Biology
Must read NCERT Notes subject-wise
- NCERT Notes for Class 12 Physics
- NCERT Notes for Class 12 Chemistry
- NCERT Notes for Class 12 Maths
- NCERT Notes for Class 12 Biology
Also, Check NCERT Books and NCERT Syllabus
Frequently Asked Questions (FAQs)
One will learn all the basics of the electromagnetic waves and their properties like radio waves, microwaves, IR rays, UV rays, gamma rays etc.
Yes, these questions and NCERT Exemplar Class 12 Physics solutions chapter 8 are highly useful in preparation of the entrance exams of both engineering and medical science.
Yes, each and every question and Class 12 Physics NCERT Exemplar solutions chapter 8 is solved in a way that is deemed fit by CBSE involving each step and diagram that gets separate marks.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters


