NCERT Books and the NCERT Syllabus for Class 12 form the foundation of board exam preparation and competitive exam readiness. Easy access to these links helps students follow the latest curriculum, understand topic-wise weightage, and prepare systematically for CBSE board examinations.
NCERT solutions for class 12 physics chapter 8 Electromagnetic Waves
Have you ever wondered how your mobile phone can pick up signals over a long distance or how sunlight makes its way in space to reach the earth? The solution to this can be found in electromagnetic waves, which were discussed in Chapter 8 of Class 12 Physics - Electromagnetic Waves. This chapter describes the nature, properties, electromagnetic spectrum and their applications in the real world.
This Story also Contains
- NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves: Download PDF
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Exercise Questions
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Additional Questions
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Higher Order Thinking Skills (HOTS) Questions
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Topics
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Important Formulae
- How Can NCERT Solutions for Class 12 Physics Chapter 8 Help in Exam Preparation?
- Approach to Solve Questions of Class 12 Physics Chapter 8 - Electromagnetic Waves
- Importance of NCERT Solutions for Class 12 Physics Chapter 8: Electromagnetic Waves
- What Students Learn from NCERT Solutions for Class 11 Physics Chapter 8: Electromagnetic Waves?
- What Extra Should Students Study Beyond NCERT For JEE/NEET?
- NCERT Solutions for Class 12 Physics Chapter-Wise
- NCERT Books and NCERT Syllabus
- NCERT Solutions Subject-wise
- NCERT Exemplar Class 12 Solutions

NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves present these concepts in a clear, simple, and step-by-step manner for better understanding. These NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves are prepared by highly qualified experts in the subject according to the current CBSE Class 12 Physics syllabus and can enable the students to learn key topics very fast and at the same time understand them best. These NCERT Solutions for Class 12 Physics Chapter 8 provide detailed answers to NCERT questions in the form of exercises, other practice questions, and concept explanations, thus very practical in enhancing fundamentals and exam results. NCERT Solutions for Class 12 Physics Chapter 8 are an excellent resource for CBSE board exam preparation as well as competitive exams like JEE and NEET, where conceptual clarity is essential.
NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves: Download PDF
The Class 12 Physics Chapter 8 - Electromagnetic Waves question answers help students gain a clear understanding of the concepts and reinforce their knowledge by giving out detailed and stepwise answers to all the questions present in the chapter. The Class 12 physics chapter 8 Electromagnetic Waves question answers are crafted according to the new NCERT syllabus and are also very beneficial in preparation for the board exams and competitive exams like JEE and NEET. You may as well download the free PDF to read continuously and revise successfully.
Class 12 Physics Chapter 8 - Electromagnetic Waves: Exercise Questions
Electromagnetic Waves class 12 question answers of textbook exercises offer detailed and easy-to-understand answers to all in-text and exercise problems. These Electromagnetic Waves class 12 question answers help students grasp key concepts, practice effectively, and prepare confidently for board exams and competitive tests like JEE and NEET.
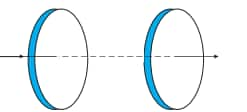
Calculate the capacitance and the rate of change of potential difference between the plates.
Answer:
Radius of the discs(r) = 12cm
Area of the discs(A) = $\pi r^{2}=\pi (0.12)^{2}=.045m^{2}$
Permittivity, $\epsilon _{0}$ = $8.85\times 10^{-12}C^{2}N^{-1}m^{2}$
Distance between the two discs = 5cm=0.05m
$Capacitance= \frac{\varepsilon _{0}A}{d}$
= $\frac{8.85\times 10^{-12}C^{2}N^{-1}m^{2}\times .045m^{2}}{0.05m}$
= $8.003\times 10^{-12}F$
=8.003 pF
$Rate\ of \ change\ of \ potential =\frac{dv}{dt}$
But
$V =\frac{Q}{C}$
Therefore,
$Rate\ of \ change\ of \ potential=\frac{d(\frac{Q}{C})}{dt}=\frac{dq}{Cdt}=\frac{i}{C}$
$=\frac{0.15A}{8.003pF}$
= $1.87\times 10^{10}Vs^{-1}$
1(b). Figure shows a capacitor made of two circular plates, each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A. Obtain the displacement current across the plates.

Answer:
The value of the displacement current will be the same as that of the conduction current, which is given to be 0.15A. Therefore, the displacement current is also 0.15A.
1.(c) Figure 8.5 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A. Is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor? Explain.

Answer:
Yes, Kirchhoff's First rule (junction rule) is valid at each plate of the capacitor. This might not seem like the case at first, but once we take into consideration both the conduction and displacement current, Kirchhoff's first rule will hold good.
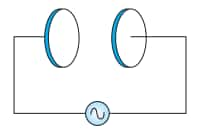
2.(a) A parallel plate capacitor made of circular plates, each of radius R = 6.0 cm, has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of $300 rad s ^{-1}$. What is the rms value of the conduction current?
Answer:
Capacitance(C) of the parallel plate capacitor = 100 pF
Voltage(V) = 230 V
Angular Frequency (ω) = $300\ rad\ s^{-1}$
$Rms\ Current(I) =\frac{Voltage}{Capacitive\ Reactance}$
$Capacitive \ Reactance(X_{c})= \frac{1}{C\omega }=\frac{1}{100\ pF\times 300\ rad\ s^{-1}}$
$X_{c}= 3.33\times 10^{7} \Omega$
$I=\frac{V}{X_{c}}=\frac{230V}{3.33\times 10^{7}\Omega }= 6.9\times 10^{-6}A$
RMS value of conduction current is $6.9\mu A$
2.(b) A parallel plate capacitor (Fig. 8.6) made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of $300 rad s ^{-1}$ Is the conduction current equal to the displacement current?

Answer:
Yes, conduction current is equal to the displacement current. This will be the case because otherwise, we will get different values of the magnetic field at the same point by taking two different surfaces and applying Ampere–Maxwell Law.
2.(c) A parallel plate capacitor (Fig. 8.6) made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of $300 rad\: \: s ^{-1}$. Determine the amplitude of B at a point 3.0 cm from the axis between the plates.

Answer:
We know Ampere-Maxwell's Law,
$\oint B\cdot \vec{dl} = \mu _{0}(i_{c}+\varepsilon _{0}\frac{d\phi _{E}}{dt})$
Between the plates conduction current $i_{c}=0$.
For a loop of radius r smaller than the radius of the discs,
$\mu _{0}\varepsilon _{0}\frac{\mathrm{d} \phi _{E}}{\mathrm{d} t}=\mu _{0}i_{d}\frac{\pi r^{2}}{\pi R^{2}}=\mu _{0}i_{d}\frac{ r^{2}}{ R^{2}}$
$B(2\pi r)=\mu _{0}i_{d}\frac{r^{2}}{R^{2}}$
$B=\mu _{0}i_{d}\frac{r}{2\pi R^{2}}$
Since we have to find the amplitude of the magnetic field, we won't use the RMS value but the maximum value of the current.
$\\i_{max}=\sqrt{2}\times i_{rms}\\$
$ i_{max}=\sqrt{2}\times6.9\mu A\\$
$ i_{max}=9.76\mu A$
$\\B_{amp}=\mu _{0}i_{max}\frac{r}{2\pi R^{2}}\\$
$ B_{amp}=\frac{4\pi\times 10^{-7}\times 9.33\times 10^{-6}\times (.03) }{2\pi\times (0.06)^{2} }\\$
$ B_{amp}=1.63\times 10^{-11}T$
The amplitude of B at a point 3.0 cm from the axis between the plates is $1.63\times 10^{-11}T$.
Answer:
The speed with which these electromagnetic waves travel in a vacuum will be the same and will be equal to $3\times 10^{8}ms^{-1}$ (speed of light in vacuum).
Answer:
Since the electromagnetic wave travels along the z-direction, its electric and magnetic field vectors are lying in the x-y plane as they are mutually perpendicular.
Frequency of wave = 30 MHz
Wavelength = $\frac{Speed\ of\ light}{Frequency}$
$=\frac{3\times 10^{8}}{30\times 10^{6}}$
$=10m$ .
Answer:
Frequency range = 7.5 MHz to 12 MHz
Speed of light = $3\times 10^{8}ms^{-1}$
Wavelength corresponding to the frequency of 7.5 MHz
=$\frac{3\times 10^{8}ms^{-1}}{7.5\times 10^{6}Hz}$
$=40m$
Wavelength corresponding to the frequency of 12 MHz =
$\frac{3\times 10^{8}ms^{-1}}{12\times 10^{6}Hz}$
$=25m$
The corresponding wavelength band is 25m to 40m.
Answer:
The frequency of the electromagnetic waves produced by the oscillation of a charged particle about a mean position is equal to the frequency of the oscillation of the charged particle. Therefore, electromagnetic waves produced will have a frequency of $10^9$ Hz.
Answer:
Magnetic Field ($B_0$ )=510 nT = 510 $\times$ $10^{-9}$ T
Speed of light(c) = 3 $\times$ $10^{8}$ $ms^{-1}$
Electric Field = $B_0$ $\times$ c
= 510 $\times$ $10^{-9}$ T $\times$ 3 $\times$ $10^{8}$ $ms^{-1}$
= 153 $NC^{-1}$
Answer:
$E_0$ = 120 NC -1
$\nu =50.0\ MHz
$Magnetic\ Field \ amplitude(B0) =\frac{E_{0}}{c}$
= $\frac{120}{3\times 10^{8}}$
$=400 nT$
Angular frequency ( $\omega$ ) = 2 $\pi \nu$
$=2$ $\times \pi \times 50$ $\times$ $10^{6}$
=3.14 $\times$ $10^{8}$ rad $s^{-1}$
Propagation constant(k)
= $\frac{2\pi }{\lambda }$
= $\frac{2\pi \nu }{\lambda\nu }$
= $\frac{\omega }{c}$
= $\frac{3.14\times 10^{8} }{3\times 10^{8}}$
=1.05 rad $m^{-1}$
Wavelength( $\lambda$ ) = $\frac{c}{\nu }$
= $\frac{3\times 10^{8}}{50\times 10^{6}}$ $= 6 m$
Assuming the electromagnetic wave propagates in the positive z-direction, the Electric field vector will be in the positive x-direction and the magnetic field vector will be in the positive y-direction, as they are mutually perpendicular and $E_{0}\times B_{0}$ gives the direction of propagation of the wave.
$\vec{E}=E_{0}sin(kx-\omega t)\hat{i}$
$= 120sin(1.05x-3.14\times 10^{8} t)NC^{-1}\hat{i}$
$\vec{B}=B_{0}sin(kx-\omega t)\hat{j}$
$= 400sin(1.05x-3.14\times 10^{8} t)\ nT\hat{j}$
Answer:
$E=h\nu=\frac{hc}{\lambda}$
$E=h\nu=\frac{6.6\times 10^{-34}\times3\times10^8}{\lambda \times1.6\times10^{-19}}eV=\frac{12.375\times 10^{-7}}{\lambda}eV$
Now substitute a different range of wavelengths in the electromagnetic spectrum to obtain the energy
| EM wave | One wavelength is taken from the range | Energy in eV |
| Radio | 1 m | $1.2375\times10^{-6}$ |
| Microwave | 1 mm | $1.2375\times10^{-3}$ |
| Infra-red | 1000 nm | 1.2375 |
| Light | 500 nm | 2.475 |
| Ultraviolet | 1nm | 1237.5 |
| X-rays | 0.01 nm | 123750 |
| Gamma rays | 0.0001 nm | 12375000 |
Answer:
Frequency( $\nu$ ) =20 $\times$ $10^{10}$ Hz
$E_0$ = 48 V$m^{-1}$
$Wavelength(\lambda) =\frac{Speed\ of\ light(c)}{Frequency (\nu )}$
= $\frac{3\times 10^{8}}{20\times 10^{10}}$
$=1.5 mm$
Answer:
The amplitude of the oscillating magnetic field(B 0 ) = $\frac{E_{0}}{c}$
$=$ $\frac{48}{3\times 10^{8}}$
$=160 nT$
Answer:
The average energy density of the Electric field(U E )
= $\frac{1}{2}\epsilon E^{2}$
= $\frac{1}{2}\epsilon (Bc)^{2}$ (as E=Bc)
= $\frac{1}{2}\epsilon \frac{B^{2}}{\mu \epsilon }$ $(c=\frac{1}{\sqrt{\mu \epsilon }})$
=$U_B$
Therefore, the average energy density of the electric field is equal to the average energy density of the Magnetic field.
Class 12 Physics Chapter 8 - Electromagnetic Waves: Additional Questions
Electromagnetic Waves NCERT Solutions of additional questions offer additional work beyond school textbook questions to learners to allow them to solidify their concept knowledge, such as the propagation of waves, energy transfer, and uses of electromagnetic waves. These are solutions which are capable of raising exam preparedness and problem-solving abilities, both on the board and competitive examinations.
Answer:
$E = \left \{ ( 3.1 N/C )\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t )] \right \} \hat i$
$E = \left \{ ( 3.1 N/C )\sin [ (\frac{\pi }{2}-(( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t ))] \right \} \hat i$
The electric field vector is in the negative x-direction, and the wave propagates in the negative y-direction.
1 (b) Suppose that the electric field part of an electromagnetic wave in vacuum is $E = \left \{ ( 3.1 N/C )\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t )] \right \} \hat i$. What is the wavelength?
Answer:
From the equation of the wave given we can infer k = 1.8 rad $m^{-1}$
$Wavelength(\lambda )=\frac{2\pi }{k}$
$=\frac{2\pi }{1.8}$
$=3.49 m$
1 (c) Suppose that the electric field part of an electromagnetic wave in vacuum is $E = \left \{ ( 3.1 N/C )\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t )] \right \} \hat i$. What is the frequency n?
Answer:
From the given equation of the electric field, we can infer angular frequency( $\omega$ ) = 5.4 $\ times$10^6 rad $s^{-1}$
$\begin{aligned} & \text { Frequency, } v=\frac{c}{\lambda}=\frac{3 \times 10^8}{3.5} \\ & \approx 85.7 \times 10^6 \mathrm{~Hz} \cong 86 \mathrm{MHz}\end{aligned}$
Answer:
From the given equation of the electric field, we can infer Electric field amplitude (E 0 ) =3.1$NC^{-1}$
$\text{Magnetic field amplitude}, (B_0) =\frac{E_{0}}{c}$
$=\frac{3.1}{3\times 10^{8}}$
=1.03 $\times$ $10^{-7}$ T
Answer:
As the electric field vector is directed along the negative x-direction and the electromagnetic wave propagates along the negative y-direction, the magnetic field vector must be directed along the negative z-direction. ( $-\hat{i}\times -\hat{k}=-\hat{j}$ )
Therefore, $\vec{B}= \left \{ B_{0}\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s )t] \right \} \hat k$
$\vec{B}= \left \{ 1.03\times 10^{-7}\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s )t] \right \}T \hat k$
Answer:
Total power which is converted into visible radiation = 5% of 100W = 5W
The above means 5J of energy is passing through the surface of a concentric sphere(with the bulb at its centre) per second.
Intensity for a sphere of radius 1m
$=\frac{5}{4\pi (1)^{2}}$
=0.398 $Wm^{-2}$
Answer:
Total power which is converted into visible radiation = 5% of 100W = 5W
The above means 5J of energy is passing through the surface of a concentric sphere(with the bulb at its centre) per second.
Intensity for a sphere of radius 10 m
$=\frac{5}{4\pi (10)^{2}}$
=3.98 $\times$ $10^{-3}$ $Wm^{-2}$
Answer:
| EM wave | One wavelength is taken from the range | Temperature $T=\frac{0.29}{\lambda}$ |
| Radio | 100 cm | $2.9\times 10^{-3}K$ |
| Microwave | 0.1cm | 2.9 K |
| Infra-red | 100000ncm | 2900K |
| Light | 50000 ncm | 5800K |
| Ultraviolet | 100ncm | $2.9\times10^{6}K$ |
| X-rays | 1 ncm | $2.9\times10^8K$ |
| Gamma rays | 0.01 nm | $2.9\times10^{10}K$ |
These numbers indicate the temperature ranges required for obtaining radiation in different parts of the spectrum
Answer:
Frequency( $\nu$ )=1057 MHz
Wavelength( $\lambda$ ) $=\frac{c}{\nu }$
$=\frac{3\times 10^{8}}{1057\times 10^{6} }$
=0.283 m
=28.3 cm
Radio waves
Answer:
Using formula, $\lambda _{m}T=0.29\ cmK$
$\lambda =\frac{0.29}{2.7}$
= 0.107cm
Microwaves.
Answer:
E=14.4 keV
Wavelength( $\lambda$ ) = $\frac{hc}{E}$
= $\frac{6.6\times 10^{-34}\times 3\times 10^{8}}{14.4\times 10^{3}\times 1.6\times 10^{-19}}$
= 0.85 $\dot{A}$
X-rays
Answer the following questions
5. (a) Long-distance radio broadcasts use short-wave bands. Why?
Answer:
Long-distance radio broadcasts use short-wave bands as these are refracted by the ionosphere.
Answer the following questions
5. (b) It is necessary to use satellites for long-distance TV transmission. Why?
Answer:
As TV signals are of high frequencies, they are not reflected by the ionosphere and therefore satellites are used to reflect them.
Answer the following questions
Answer:
X-rays are absorbed by the atmosphere, and therefore, the source of X-rays must lie outside the atmosphere to carry out X-ray astronomy. Therefore, satellites orbiting the earth are necessary, but radio waves and visible light can penetrate through the atmosphere, and therefore, optical and radio telescopes can be built on the ground.
Answer the following questions
5. (d) The small ozone layer on top of the stratosphere is crucial for human survival. Why?
Answer:
The small ozone layer on top of the stratosphere is crucial for human survival as it absorbs the ultraviolet radiation coming from the sun, which is very harmful to humans.
Answer the following questions
Answer:
If the Earth did not have an atmosphere, its average surface temperature would be lower than it is now, as in the absence of an atmosphere, there would be no greenhouse effect.
Answer the following questions
Answer:
The use of nuclear weapons would cause the formation of smoke clouds, preventing the light from the sun from reaching Earth's surface, and it would also deplete the atmosphere and therefore stop the greenhouse effect and thus doubling the cooling effect.
Class 12 Physics Chapter 8 - Electromagnetic Waves: Higher Order Thinking Skills (HOTS) Questions
Chapter 8 Higher Order Thinking Skills (HOTS) Questions provide students with an opportunity to think beyond ordinary exercises and think critically in understanding electromagnetic waves. These Electromagnetic Waves class 12 question answers also assist students to apply concepts in real life and prepare themselves well for both board exams as well as competitive ones like JEE and NEET.
Q1. A red LED emits light at 0.2 watts uniformly around it. The amplitude of the electric field of the light at a distance of 3 m from the diode is ___ V/m.
Answer:
$I=P / 4 \pi r^2$ and $p_{avg}=\frac{1}{2} \varepsilon_0 E_{o}^2$
$\therefore P / 4 \pi r^2=\left(\frac{1}{2}\right) \mathcal{E}_0 E_0^2 C$
Or $E_0=\sqrt{\frac{2 P}{4 \pi \varepsilon_0 r^2 C}}$
$\begin{aligned} & \text { Here } p=0.2 \mathrm{w}, r=3 \mathrm{~m}, c=3 \times 10^8 \mathrm{~ms}^{-2} \\ & \frac{1}{4} \pi \varepsilon_0=9 \times 10^9\end{aligned}$
$\begin{aligned} & E_0=\sqrt{\frac{2 \times 0.2 \times 9 \times 10^9}{9 \times 3 \times 10^8}} \\ & E_0=\sqrt{\frac{0.4 \times 9 \times 10^9}{27 \times 10^8}} \\ & E_0=\sqrt{\frac{36}{27}}\end{aligned}$
$E_0=1.15 \mathrm{~v} / \mathrm{m}$
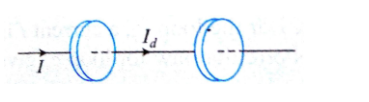
Q2. The following figure shows a capacitor made of two circular plates. The capacitor is being charged by an external source which supplies a constant current equal to 0.15 A. What is the displacement current (in amperes) across plates?
Answer:
As we know,
Displacement current
$I_d=\frac{\varepsilon_0 d \phi_c}{d t}$
But $\phi_E=E A=\frac{q}{A \varepsilon_0} A=\frac{q}{\varepsilon_0}$
$\therefore \quad I_d=\varepsilon_0 \frac{d}{d t}\left(\frac{q}{\varepsilon_0}\right)=\frac{\varepsilon_0}{\varepsilon_0} \frac{d q}{d t}=\frac{d q}{d t}=I$
Here $I=0.15 \mathrm{~A} \quad \therefore I_d=0.15 \mathrm{~A}$
Q3. A radiation of 200 W is incident on a surface which is 60% reflecting and 40% absorbing. The total force on the surface is
Answer:
Force exerted by incident radiation is $F=\frac{P}{C}$ where $P$ is the power of radiation and $C$ is the velocity of light. For absorbed radiations are $40 \%$ then exerted force is $F_{a b s}=\frac{0.4 P}{c}$ and $60 \%$ part of radiations is reflected by the surface, so force exerted by theses radiations is $ F_{r e f}=2 \times \frac{0.6 P}{C}=\frac{1.2 P}{C} $ Then total force exerted by radiations on the surface is $ \begin{aligned} & F_{\text {total }}=F_{\text {ref }}+F_{\text {abs }} \\ & =\frac{1.2 P}{c}+\frac{0.4 P}{c}=\frac{1.6 P}{c} \\ & =\frac{1.6 \times 200}{3 \times 10^8}=1.07 \times 10^{-6} \mathrm{~N} \end{aligned} $
Q4. The magnetic field of a plane electromagnetic wave is given by :
$
\vec{B}=B_0[\cos (k z-\omega t)] \hat{i}+B_1 \cos (k z+\omega t) \hat{j}
$
where $B_0=3 \times 10^{-5} T$ and $B_1=2 \times 10^{-6} \mathrm{~T}$.
The rms value of the force (in Newton) experienced by a stationary charge $Q=10^{-4} C$ at $Z=0$ is closest to (up to one decimal).
Answer:
$
\begin{aligned}
& B=B_0 \cos (k x-\omega t) \hat{i}+B_1 \cos (k z+\omega t) \hat{j} \\
& B_0=3 \times 10^{-5} T \\
& B_1=2 \times 10^{-6} T
\end{aligned}
$
Amplitude of resultant magnetic field $=B^{\prime}=\sqrt{B_o^2+B_1^2}$
$
\begin{aligned}
Q & =10^{-4} C \\
F_{r m s} & =Q E_{r m s}=Q\left(c B_{r m s}^{\prime}\right) \\
F_{r m s} & =Q \sqrt{\left(\frac{C B_0}{\sqrt{2}}\right)^2+\left(\frac{C B_1}{\sqrt{2}}\right)^2} \\
& =10^{-4} \times \frac{3 \times 10^8}{\sqrt{2}} \sqrt{\left(3 \times 10^{-5}\right)^2+\left(2 \times 10^{-6}\right)^2}
\end{aligned}
$
$
\begin{aligned}
& =10^{-4} \times \frac{3 \times 10^8}{\sqrt{2}} \sqrt{9 \times 10^{-10}+4 \times 10^{-12}} \\
& =10^{-4} \times \frac{3 \times 10^8}{\sqrt{2}} \sqrt{900 \times 10^{-12}+4 \times 10^{-12}} \\
& =\frac{3 \times 10^4}{\sqrt{2}} \sqrt{904} \times 10^{-6} \\
& =0.6 \mathrm{~N}
\end{aligned}
$
Q5. Two light waves are given by, $E_1=2 \sin (100 \pi t-k x+30)$ and $E_2=3 \cos (200 \pi t-k x+60)$. The ratio of the intensity of the first wave to that of the second wave is :
Answer:
As we learned
Intensity of EM wave -
$
I=\frac{1}{2} \epsilon_o E_o^2 c
$
where
$\epsilon_o=$ Permittivity of free space
$E_o=$ Electric field amplitude
$\mathrm{c}=$ Speed of light in vacuum
so
$
I \propto A^2 \therefore \frac{I_1}{I_2}=\frac{2^2}{3^2}=4 / 9
$
Also Read
- NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves
- NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF
Class 12 Physics Chapter 8 - Electromagnetic Waves: Topics
Class 12 Physics Chapter 8 - Electromagnetic Waves is to explain the oscillation of electric and magnetic fields in order to transmit the energy across space. The Class 12 Physics NCERT Chapter 8 Electromagnetic Waves identifies the source, characteristics and uses of electromagnetic waves, which are the backbone of modern communication systems. These topics are not just some good preparation for board exams, but also a good way of learning the concepts that are helpful in JEE and NEET.
8.1 Introduction
8.2 Displacement current
8.3 Electromagnetic waves
8.3.1 Sources of electromagnetic waves
8.3.2 Nature of electromagnetic waves
8.4 Electromagnetic spectrum
8.4.1 Radio waves
8.4.2 Microwaves
8.4.3 Infrared waves
8.4.4 Visible rays
8.4.5 Ultraviolet rays
8.4.6 X-rays
8.4.7 Gamma rays
Class 12 Physics Chapter 8 - Electromagnetic Waves: Important Formulae
Class 12 Physics Chapter 8 Electromagnetic Waves explains how electric and magnetic fields combine to form waves that travel through space without needing any medium. Class 12 Physics NCERT Chapter 8 Electromagnetic Waves introduces students to Maxwell’s equations, displacement current, and the nature of the electromagnetic spectrum. Learning the important formulas from this chapter helps students solve numerical problems quickly and understand the relationship between wavelength, frequency, and energy in different types of electromagnetic waves.
Displacement current:
$
I_d=\varepsilon_0 \frac{d \Phi_E}{d t}
$
Maxwell's equations (free space):
$
\begin{aligned}
& \nabla \cdot \vec{E}=\frac{\rho}{\varepsilon_0} \\
& \nabla \cdot \vec{B}=0 \\
& \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} \\
& \nabla \times \vec{B}=\mu_0 \vec{J}+\mu_0 \varepsilon_0 \frac{\partial \vec{E}}{\partial t}
\end{aligned}
$
Speed of light:
In vacuum: $c=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}$
In medium: $v=\frac{c}{n}$
Angular frequency: $\omega=2 \pi f$
Wave number: $k=\frac{2 \pi}{\lambda}$
Energy densities:
Electric: $u_E=\frac{1}{2} \varepsilon_0 E^2$
Magnetic: $u_B=\frac{1}{2} \frac{B^2}{\mu_0}$
Total: $u=u_E+u_B=\varepsilon_0 E^2=\frac{B^2}{\mu_0}$
How Can NCERT Solutions for Class 12 Physics Chapter 8 Help in Exam Preparation?
Electromagnetic Waves class 12 question answers can be of great help to the students who want to perform well in their board examinations. In this chapter, the connection between magnetic and electric fields is established, and how electromagnetic waves are generated by changing fields is explained, which is a fundamental concept in the field of physics in the modern world. These Class 12 physics Electromagnetic Waves question answers can help students to have a clear idea of major concepts like the electromagnetic spectrum, characteristics of various waves, as well as their applications in various technologies such as radio, television, and satellites.
Conceptual, numerical and application questions are included in these solutions as well, which intensify the problem-solving and analytical thinking. All NCERT Electromagnetic Waves Class 12 Solutions are presented in simple and exam-oriented language to assist students in writing accurate and comprehensive answers whenever undertaking exams. Moreover, revising by Electromagnetic Waves Class 12 NCERT Solutions provides total coverage of the syllabus and enables students to remember key points easily during the last-minute revision, hence one can be confident about answering questions in the board as well as in competitive exams more effectively.
Approach to Solve Questions of Class 12 Physics Chapter 8 - Electromagnetic Waves
The electromagnetic waves are the foundation of the modern world of communication, medical science and even the transfer of energy in nature. During the process of answering questions in this chapter, the students are required to concentrate on the properties of waves and their equations and their application in real life, rather than memorisation. The systematic approach will assist in addressing the conceptual as well as the numerical issues without any problems.
- Revise Basics of Maxwell's Equations - Learn how electric and magnetic fields that vary with time produce electromagnetic waves.
- Memorise Important Formulas -Speed of EM waves, relationship between electric field (E) and magnetic field (B), energy density.
- Know the Spectrum - Learn the frequency, wavelength ranges, and other uses of various components of the electromagnetic spectrum (radio, microwave, infrared, visible, UV, X-ray, gamma).
- Concentrate on Wave Properties: Polarisation, reflection, refraction, and interaction of EM waves with objects.
- Solve Conceptual Problems -Use reasoning to solve problems in the real world, such as communication devices, satellites, and medical imaging.
- Step-by-Step approach to solving Numerical Problems - It is always important to begin with the known quantities (E, B, c, f) and use relations in a systematic manner.
- Practice Past Year questions -Work on JEE/ NEET and CBSE board questions to be acquainted with concepts that are commonly asked.
- Make Short Notes - Summarise formulas, spectrum chart, and key concepts for quick revision.
Importance of NCERT Solutions for Class 12 Physics Chapter 8: Electromagnetic Waves
Electromagnetic Waves Class 12 Questions and Answers are significant since this chapter provides the nature, properties, and uses of electromagnetic radiation, which is commonly employed in modern technology and communications systems.
- Helps students have a clear understanding of what is meant by electromagnetic waves and the way in which they are generated when the electric and magnetic fields oscillate.
- Describes the electromagnetic spectrum in a systematic manner, which incorporates radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays.
- Constructs conceptual understanding regarding the concepts of Maxwell on electromagnetic waves and their propagation in free space.
- Relevant to the CBSE board exams since this chapter consists mostly of conceptual, short-answer, and application-based questions.
- Useful for competitive exams like JEE and NEET, where questions from the electromagnetic spectrum and wave properties are frequently asked.
- Helps students understand applications and risks of various electromagnetic waves, which are usually asked in examinations.
- Improves retention of definitions, characteristics, and comparisons through well-structured explanations.
- Relates concepts of physics to real-life observations like wireless communication, medical imaging, remote sensing and satellites.
What Students Learn from NCERT Solutions for Class 11 Physics Chapter 8: Electromagnetic Waves?
The chapter Electromagnetic Waves assists students in understanding the possibility of energy to move through space in the form of waves without having a material medium. Students can acquire a conceptual understanding of this chapter that uses a theory, along with exam-oriented knowledge of this chapter, with the assistance of the Electromagnetic Waves NCERT Solutions.
- Find out what electromagnetic waves are and how they are formed as a result of vibrating electric and magnetic fields.
- Know how the electric and magnetic mutual fields work with each other in an electromagnetic wave.
- Learn the characteristics of electromagnetic waves, including speed, wavelength, frequency and transverse nature.
- Learn about the electromagnetic spectrum and the correct order of different types of waves.
- Know the applications and the uses of radio waves, microwaves, infrared, visible light, ultraviolet, X-rays and gamma rays.
- Have a clear understanding of the fact that Maxwell predicted the existence of electromagnetic waves and their usefulness.
- Enhance the knowledge of how to solve theory-based and application-based questions, which are normally asked in examinations.
- Develop a good conceptual knowledge that can be applied in the board exams as well as competitive exams such as the JEE and NEET.
What Extra Should Students Study Beyond NCERT For JEE/NEET?
Beyond NCERT, students preparing for JEE/NEET should study additional concepts like Energy Density and Intensity of Electromagnetic Waves, which explain how energy is distributed in electric and magnetic fields and how it propagates through space. Understanding these topics enhances conceptual clarity and equips students to solve advanced numerical and application-based problems in competitive exams.
NCERT Solutions for Class 12 Physics Chapter-Wise
NCERT Class 12 Physics Solutions Chapter-wise links provide a complete guide to all chapters, making it easier for students to access solved exercises, important formulas, and key concepts in one place. These solutions are designed to help students prepare effectively for board exams, JEE, NEET, and other competitive tests.
NCERT Books and NCERT Syllabus
NCERT Solutions Subject-wise
NCERT Solutions subject-wise links provide easy access to chapter-wise answers for all major subjects in one place. These solutions help students understand concepts clearly, practise textbook questions effectively, and prepare confidently for exams
NCERT Exemplar Class 12 Solutions
NCERT Exemplar Solutions for Class 12 provide advanced and application-based questions to strengthen conceptual understanding. These subject-wise links help students practise higher-level problems and prepare effectively for board exams as well as competitive exams like JEE and NEET.
Frequently Asked Questions (FAQs)
Before starting the preparation of NCERT class 12 chapter 8 it is better to have an idea of chapters 1 to 7. Chapter 1 to 7 is interconnected.
One question from chapter 8 electromagnetic waves can be expected for the NEET exam. The questions can be theoretical or numerical.
From the chapter on electromagnetic waves, one question can be expected for JEE Main. More than one question can also be asked.
3 to 5 marks questions are asked from class 12 chapter electromagnetic waves for CBSE board exams.
Experts at Careers360 have created the chapter 8 physics class 12 ncert solutions after completing extensive research on each concept. To assist students perform well on class assignments and board exams, every small element is well addressed. Additionally, it enables students to successfully complete their tasks on time.
Light is produced by the acceleration of charged particles (photons); therefore, by the law of electromagnetism, light is an electromagnetic wave.
Electromagnetic waves have a vast range of practical everyday applications that includes such diverse uses as communication by cell phone and radio broadcasting, WiFi, cooking, vision, medical imaging, and treating cancer.
The radio waves and the microwaves are normally applied in communication such as radio broadcasting, television, mobile phones, and satellite communication.
The magnetic field and electric field are oscillating at right angles and in opposite directions to the direction of wave propagation.
Electromagnetic waves are produced whenever electric charges accelerate (change their speed or direction). Any moving charge that is vibrating or oscillating becomes a source of electromagnetic radiation.
Questions related to CBSE Class 12th
On Question asked by student community
Dear Student,
Please go through the link to check 12th CBSE Chemistry question paper: https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers-class-12-chemistry
The Second Language English paper for the 2025-26 academic session (Summative Assessment 2 or SA-2 phase) focused on comprehension, grammar, and literature.
Exam Pattern & Marking Scheme (Class 8 English)
The second language English paper is divided into four main sections, totalling 80 Marks (for most state boards like Karnataka)
The Class 9th Social Science (SST) annual exam 2025-26 follows a standardised structure across CBSE and most State Boards. The exams for most of the boards are being held in February- March 2026. Check the marking scheme here for the SST exams
|
Section |
Type of Questions |
Number of Questions |
Marks |
Dear Student,
You can check Class 12 Physics CBSE Hindi medium PYQs here:
CBSE Class 12 Previous Year Question Papers With Solutions PDF Download
I am assuming the CBSE Board Physics Exam 2026 question paper. Download it here .
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
