Aakash Repeater Courses
Take Aakash iACST and get instant scholarship on coaching programs.
NCERT Exemplar Class 10 Maths Solutions chapter 12 discusses the method to determine the surface area and volume of various three-dimensional objects. This chapter helps us to understand how to calculate the area related to covering a solid object and the space it occupies. The concepts we study in this chapter are crucial for solving practical problems related to geometry and real-life applications. These three-dimensional objects can be cones, spheres, or cylinders. In this article, we will deal with many questions such as, 'How do we calculate the surface area and volume of different solids like cubes, cylinders, cones, and spheres?', What are the formulas for surface area and volume?', and 'How do we apply these formulas in different scenarios?' These consist of detailed solutions to study and understand the NCERT class 10 Maths. These NCERT exemplar class 10 Maths chapter 12 solutions are prepared by our skilled subject matter experts.
Don't Miss: Best Courses after 10th | Competitive Exams after 10th
Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash
The NCERT Exemplar Class 10 Maths chapter 12 solutions are beneficial for understanding of concepts of surface area and volume due to their comprehensive nature. The CBSE Syllabus Class 10 Maths is the reference for NCERT Exemplar Class 10 Maths solutions chapter 12.
| Class 10 Maths Chapter 12 exemplar solutions Exercise: 12.1 Page number: 138-140 Total questions: 20 |
A cylindrical pencil sharpened at one edge is the combination of
(A) a cone and a cylinder (B) frustum of a cone and a cylinder
(C) a hemisphere and a cylinder (D), two cylinders.
A Surahi is the combination of
(A) a sphere and a cylinder (B) a hemisphere and a cylinder
(C) two hemispheres (D) a cylinder and a cone.
A plumbline (sahul) is the combination of
(A) a cone and a cylinder (B) a hemisphere and a cone
(C) frustum of a cone and a cylinder (D) sphere and cylinder
The shape of a glass (tumbler) (see figure) is usually in the form of
(A) a cone (B) frustum of a cone
(C) a cylinder (D) a sphere




The shape of a gilli, in the gilli-danda game (See figure), is a combination of
(A) two cylinders (B) a cone and a cylinder
(C) two cones and a cylinder (D) two cylinders and a cone
A shuttle cock used for playing badminton has the shape of the combination of
(A) a cylinder and a sphere
(B) a cylinder and a hemisphere
(C) a sphere and a cone
(D) frustum of a cone and a hemisphere

A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called
(A) a frustum of a cone (B) cone
(C) cylinder (D) sphere

A hollow cube of internal edge 22cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that
(A) 142296 (B) 142396 (C) 142496 (D) 142596
A solid piece of iron in the form of a cuboid of dimensions
(A) 21cm (B) 23cm (C) 25cm (D) 19cm
A mason constructs a wall of dimensions
(A) 11100 (B) 11200 (C) 11000 (D) 11300
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(A) 4 cm (B) 3 cm (C) 2 cm (D) 6 cm
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is
(A) 4950 cm2 (B) 4951 cm2 (C) 4952 cm2 (D) 4953 cm2
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is
(A) 0.36 cm3 (B) 0.35 cm3 (C) 0.34 cm3 (D) 0.33 cm3
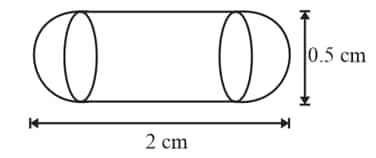
Diameter of hemisphere = 0.5 cm
Similarly radius of cylinder = 0.25
Height = 2- 0.25 -0.25
= 2- 0.5
=1.5 cm
The total volume of capsule = volume of two hemispheres + volume of the cylinder
= 0.359cm3
=0.36cm3 (approximate)
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is
(A)

A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter
(A) r cm (B) 2r cm (C) h cm (D) 2h cm

During conversion of a solid from one shape to another, the volume of the new shape will
(A) increase (B) decrease
(C) remain unaltered (D) be doubled
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is
(A) 32.7 litres (B) 33.7 litres (C) 34.7 litres (D) 31.7 litres
In a right circular cone, the cross-section made by a plane parallel to the base is a
(A) circle (B) frustum of a cone
(C) sphere (D) hemisphere

Volumes of two spheres are in the ratio 64:27. The ratio of their surface areas is
(A) 3 : 4 (B) 4 : 3 (C) 9 : 16 (D) 16 : 9
| Class 10 Maths chapter 12 exemplar solutions Exercise: 12.2 Page number: 142-143 Total questions: 8 |
Write ‘True’ or ‘False’ and justify your answer in the following:
Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is


Write ‘True’ or ‘False’ and justify your answer in the following :
A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is


Write ‘True’ or ‘False’ and justify your answer in the following :
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is


Write ‘True’ or ‘False’ and justify your answer in the following :
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is

Write ‘True’ or ‘False’ and justify your answer in the following:
The volume of the frustum of a cone is

Write ‘True’ or ‘False’ and justify your answer in the following:
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the Figure is
Write ‘True’ or ‘False’ and justify your answer in the following:
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surfacearea of cylinder

| Class 10 Maths Chapter 12 exemplar solutions Exercise: 12.3 Page number: 146-147 Total questions: 14 |
How many shots each having a diameter of 3 cm can be made from a cuboidal lead solid of dimensions

It is given that volume of cube = 64 cm3
So the side of the two cubes are 4 cm
The cuboid formed by joining two cubes.
The surface area of the cuboid


Answer 12960
Solution
Length of wall
Breadth of wall
Height of wall
The volume of wall = length × breadth × height
Remaining volume = 57600000 – 5760000 = 51840000 cm3
Length of brick = 25 cm
Breadth of brick = 16cm
Height of brick = 10cm
Volume of brick = length × breadth × height
= 25 × 16 × 10 = 4000 cm3
Hence, the number of bricks is 12960.
| Class 10 Maths Chapter 12 exemplar solutions Exercise: 12.4 Page number: 150-152 Total questions: 20 |
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used upon writing 3300 words on average. How many words can be written in a bottle of ink containing one-fifth of a litre?
3300 words can be written with 0.001375 L of ink
So with 1L of ink 3300/0.001375 words can be written=2400000
So with 1/5th of a litter 2400000/5 words can be written=48000
Given: Volume of building
Let total height above the floor = h
Hemisphere‘s diameter = h (given)
Height of cylinder = total height – the height of hemisphere
Volume
According to question
The volume of building = Volume of cylinder + volume of the hemisphere
NCERT exemplar Class 10 chapter 12 Maths solutions covers the following topics:
Take Aakash iACST and get instant scholarship on coaching programs.
NCERT exemplar Class 10 Maths solutions chapter 12 pdf download is a free-to-use feature that provides the students with the facility to study the NCERT exemplar Class 10 Maths chapter 12 in an offline environment.
Here, you can find solutions to NCERT class 10 Maths and Science.
Here, you can find notes of NCERT class 10 Maths and Science.
Here, you can find the syllabus and books of the NCERT class 10 Maths and Science.
Ice cream cones can be seen as a combination of a hemisphere and a cone in simplified form. We know the volume of cone and volume of the hemisphere, so we can find out its complete volume.
We can find out the volume of sharpened pencil by assuming it as a combination of cylinder and a cone.
The chapter Surface Areas and Volumes is vital for Board examinations as it holds around 8-10% weightage of the whole paper.
It is highly suggested that students practice and study every topic covered in NCERT exemplar Class 10 Maths solutions chapter 12 to score high in Surface Areas and Volumes.
Application Date:24 July,2025 - 23 August,2025
Application Date:24 July,2025 - 23 August,2025
Hello
Since you are a domicile of Karnataka and have studied under the Karnataka State Board for 11th and 12th , you are eligible for Karnataka State Quota for admission to various colleges in the state.
1. KCET (Karnataka Common Entrance Test): You must appear for the KCET exam, which is required for admission to undergraduate professional courses like engineering, medical, and other streams. Your exam score and rank will determine your eligibility for counseling.
2. Minority Income under 5 Lakh : If you are from a minority community and your family's income is below 5 lakh, you may be eligible for fee concessions or other benefits depending on the specific institution. Some colleges offer reservations or other advantages for students in this category.
3. Counseling and Seat Allocation:
After the KCET exam, you will need to participate in online counseling.
You need to select your preferred colleges and courses.
Seat allocation will be based on your rank , the availability of seats in your chosen colleges and your preferences.
4. Required Documents :
Domicile Certificate (proof that you are a resident of Karnataka).
Income Certificate (for minority category benefits).
Marksheets (11th and 12th from the Karnataka State Board).
KCET Admit Card and Scorecard.
This process will allow you to secure a seat based on your KCET performance and your category .
check link for more details
https://medicine.careers360.com/neet-college-predictor
Hope this helps you .
Hello Aspirant, Hope your doing great, your question was incomplete and regarding what exam your asking.
Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.
hello Zaid,
Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.
best of luck!
According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.
You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Take Aakash iACST and get instant scholarship on coaching programs.

This ebook serves as a valuable study guide for NEET 2025 exam.

This e-book offers NEET PYQ and serves as an indispensable NEET study material.

As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
As per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE