NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids

Edited By Vishal kumar | Updated on Sep 05, 2023 10:21 AM IST

NCERT Solutions Class 11 Physics Chapter 10 – Download Free PDF

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids: If you're a Class 11 student in search of NCERT solutions, you're in the right spot. Here, on the Careers360 page, you can find extensive class 11 physics chapter 10 exercise solutions available for free, complete with detailed step-by-step explanations. This collection covers a total of thirty questions, including those from 10.1 to 10.20 for exercise questions and 10.20 to 10.30 for additional exercises.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

NEET Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | ALLEN

This Story also Contains

NCERT Solutions Class 11 Physics Chapter 10 – Download Free PDF
NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids
Mechanical properties of fluids class 11 NCERT solutions - Exercise
NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids - Additional Exercise
NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids
Benefits of NCERT solutions for class 11 physics chapter 10 mechanical properties of fluids:
NCERT Solutions for Class 11 Subject wise

We all know that fluids do not have a particular shape. The shape of the fluid is decided by the shape of the container. In the solutions of NCERT Class 11 Physics Chapter 10 Mechanical Properties of Fluids, questions related to the properties of fluids (liquid and gas) and certain laws associated with the properties are discussed. Also, questions on all the topics of the chapter Mechanical Properties of Fluids Class 11 are covered in the CBSE NCERT solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids and are very important from the exam point of view.

We all have heard the term pressure; Pascal's law is related to pressure and this law states that pressure in a fluid at rest is the same at all points which are at the same height. A change in pressure applied to an enclosed fluid is transmitted to every point of the fluid and the walls of the containing vessel container. One of the applications of this law is a Hydraulic Lift. Let's try to find a few more examples in NCERT by yourself. The main aim of the mechanical properties of fluids NCERT solutions is to check the depth of understanding of the concepts and formulas studied in the chapter. Careers360 has made the mechanical properties of fluids class 11 NCERT solutions available in PDF format, which can be accessed by students anytime and anywhere, to aid in their understanding of the chapter and its associated questions.

NCERT Class 11 Physics Chapter 10 Exercise Solutions PDF download for free.

**According to the CBSE Syllabus for the academic year 2023-24, the chapter you previously referred to as Chapter 10, " Mechanical Properties of Fluids ," has been renumbered as Chapter 9.

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids

Download PDF

Mechanical properties of fluids class 11 NCERT solutions - Exercise

Q 10.1 (a) Explain why

The blood pressure in humans is greater at the fe et than at the brain

Answer:

The pressure in a fluid column increases with the height of the column, as the height of the blood column is more than that for the brain the blood pressure in feet is more than the blood pressure in the brain.

Q 10.1 (b) Explain why

Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km

Answer:

This is because the air density does not remain the same in the atmosphere. It decreases exponentially as height increases.

Q 10.1 (c) Explain why

Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.

Answer:

When a force is applied on fluid the pressure which gets generated gets uniformly transmitted to all directions and therefore has no particular direction and is a scalar quantity. We talk of division of force with area only while considering the magnitudes. The actual vector form of the relation is $\vec{F}=p\vec{A}$

Q 10.2 (a) Explain why

(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute.

Answer:

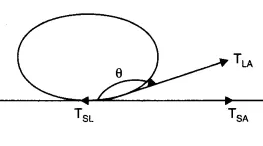
1650445487018

T _SL = Surface tension corresponding to the solid-liquid layer

T _LA = Surface tension corresponding to liquid-air layer

T _SA = Surface tension corresponding to solid-air layer

The angle of contact is $\Theta$

Since the liquid is not flowing over the solid surface the components of T _SL , T _LA and T _SA along the solid surface must cancel out each other.

$\\T_{SL}+T_{LA}cos\Theta =T_{SA}\\ cos\Theta =\frac{T_{SA}-T_{SL}}{T_{LA}}$

In case of mercury T _SA < T _SL and therefore $cos\Theta <0$ and therefore $\Theta >\frac{\pi }{2}$ i.e the angle of contact of mercury with glass is obtuse.

Q 10.2 (b) Explain why

(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)

Answer:

Cohesive forces between water molecules is much lesser than adhesive forces between water and glass molecules and that's why water tends to spread out on glass whereas cohesive forces within mercury is comparable to adhesive forces between mercury and glass and that's why mercury tends to form drops.

Q 10.2 (c) Explain why

Answer:

Surface tension is the force acting per unit length at the interface of a liquid and another surface. Since this force itself is independent of area, the surface tension is also independent of area.

Q 10.2 (d) Explain why

(d) Water with detergent dissolved in it should have small angles of contact.

Answer:

As we know detergent with water rises very fast in capillaries of clothes which is only possible when cosine of the angle of contact is the large i.e. angle of contact must be small.

Q 10.2 (e) Explain why

(e) A drop of liquid under no external forces is always spherical in shape

Answer:

While in a spherical shape the surface area of the drop of liquid will be minimum and thus the surface energy would be minimum. A system always tends to be in a state of minimum energy and that's why in the absence of external forces a drop of liquid is always spherical in shape.

Q 10.3 Fill in the blanks using the word(s) from the list appended with each statement:

(a) Surface tension of liquids generally ... with temperatures (increases / decreases)

(b) Viscosity of gases ... with temperature, whereas viscosity of liquids ... with temperature (increases / decreases)

(c) For solids with elastic modulus of rigidity, the shearing force is proportional to ... , while for fluids it is proportional to ... (shear strain / rate of shear strain)

(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle)

(e) For the model of a plane in a wind tunnel, turbulence occurs at a ... speed for turbulence for an actual plane (greater / smaller)

Answer:

(a) The surface tension of liquids generally decreases with temperatures.

(b) The viscosity of gases increases with temperature, whereas the viscosity of liquids decreases with temperature.

(c) For solids with elastic modulus of rigidity, the shearing force is proportional to shear strain , while for fluids it is proportional to the rate of shear strain .

(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows from conservation of mass while the decrease of pressure there follows from Bernoulli’s principle .

(e) For the model of a plane in a wind tunnel, turbulence occurs at a greater speed for turbulence for an actual plane.

Q 10.4 (a) Explain why

(a) To keep a piece of paper horizontal, you should blow over, not under, it

Answer:

As per Bernoulli's principle when we blow over a piece of paper the pressure there decreases while the pressure under the piece of the paper remains the same and that's why it remains horizontal.

Q 10.4 (b) Explain why

(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers

Answer:

This is because when we cover the tap there are very small gaps remaining for the water to escape and it comes out at very high velocity in accordance with the equation of continuity.

Q 10.4 (c) Explain why

(c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection

Answer:

Because of the extremely small size of the opening of a needle, its size can control the flow with more precision than the thumbs of a doctor.

According to the equation of continuity area * velocity= constant. if the area is very small the velocity must be large. Thus if the area is small flow becomes smooth

Q 10.4 (d) Explain why

(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel

Answer:

Through a small area, velocity will be large. A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel in accordance with the law of conservation of linear momentum.

Q 10.4 (e) Explain why

(e) A spinning cricket ball in air does not follow a parabolic trajectory

Answer:

The ball while travelling rotates about its axis as well causing a difference in air velocities at different points around it thus creating pressure difference which results in external forces. In the absence of air, a ball would have travelled along the expected parabolic path.

Q 10.5 A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?

Answer:

Mass of the girl m = 50 kg.

Gravitational acceleration g = 9.8 m s ^-2

Weight of the girl (W) , mg = 490 N

$\\Pressure=\frac{Force}{Area}\\ =\frac{490}{\pi \left ( \frac{1\times 10^{-2}}{2} \right )^{2}}\\ =6.24\times 10^{6}Pa$

Q 10.6 Torricelli's barometer used mercury. Pascal duplicated it using French wine of density 984 kg m ^-3 . Determine the height of the wine column for normal atmospheric pressure.

Answer:

Atmospheric pressure is $P=1.01\times 10^{5}Pa$

The density of French wine $\rho_{w}= 984\ kg\ m^{-3}$

Height of the wine column h _w would be

$\\h_{w}=\frac{P}{\rho _{w}g}\\h_{w}=\frac{1.01\times 10^{5}}{984\times 9.8}\\ h_{w}=10.474m$

Q 10.7 A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.

Answer:

The density of water is $\rho _{w}=1000\ kg\ m^{-3}$

Depth of the ocean is 3 km

The pressure at the bottom of the ocean would be

$\\P=\rho _{w}gh\\ P=1000\times 9.8\times 3\times 1000 \\P=2.94\times 10^{7}Pa$

The above value is much lesser than the maximum stress the structure can withstand and therefore it is suitable for putting up on top of an oil well in the ocean.

Q 10.8 A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm ² . What maximum pressure would the smaller piston have to bear?

Answer:

Maximum Pressure which the piston would have to bear is

$\\P_{max}=\frac{Maximum\ weight\ of\ a\ car}{Area\ of\ the\ piston}\\ =\frac{3000\times 9.8}{425\times 10^{-4}}\\ =6.917\times 10^{5} Pa$

Q 10.9 A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?

Answer:

Since the mercury columns in the two arms are equal the pressure exerted by the water and the spirit column must be the same.

$\\h_{w}\rho _{w}g=h_{s}\rho _{s}g\\ \frac{\rho _{s}}{\rho _{w}}=\frac{h_{w}}{h_{s}}\\ \frac{\rho _{s}}{\rho _{w}}=\frac{10}{12.5}\\ \frac{\rho _{s}}{\rho _{w}}=0.8$

Therefore the specific gravity of spirit is 0.8.

Q 10.10 In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6)

Answer:

Let the difference in the levels of mercury in the two arms be h _Hg

$\\(\rho _{w}-\rho _{s})gh=\rho _{Hg}gh_{Hg}\\ \left ( 1-\frac{\rho _{s}}{\rho _{w}} \right )h=\frac{\rho _{Hg}}{\rho _{w}}h_{Hg}\\ (1-0.8)\times 15=13.68h_{Hg}\\ h_{Hg}=\frac{0.2\times 15}{13.6}\\ h_{Hg}=0.22cm$

Q 10.11 Can Bernoulli’s equation be used to describe the flow of water through a rapid in a river? Explain.

Answer:

No. Bernoulli's equation can be used only to describe streamline flow and the flow of water in a river is turbulent.

Q 10.12 Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain

Answer:

No, unless the atmospheric pressures at the two points where Bernoulli’s equation is applied are significantly different.

Q 10.13 Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 × 10 ^-3 kg s ^-1 , what is the pressure difference between the two ends of the tube ? (Density of glycerine = 1.3 × 103 kg m ^-3 and viscosity of glycerine = 0.83 Pa s). [You may also like to check if the assumption of laminar flow in the tube is correct].

Answer:

The volumetric flow rate of glycerine flow would be given by

$\\V=\frac{Amount\ of\ glycerine\ flow\ per\ second\ }{Density\ of\ glycerine}\\ V=\frac{M}{\rho }\\ V=\frac{4\times 10^{-3}}{1.3\times 10^{3}}\\ V=3.08\times 10^{-6}ms^{-1}$

The viscosity of glycerine is $\eta =0.83\ Pa\ s$

Assuming Laminar flow for a tube of radius r, length l, having pressure difference P across its ends a fluid with viscosity $\eta$ would flow through it with a volumetric rate of

$\\V=\frac{\pi Pr^{4}}{8\eta l}\\ P=\frac{8V\eta l}{\pi r^{4}}\\ P=\frac{8\times 3.08\times 10^{-6}\times 0.83}{\pi \times (10^{-2})^{4}}\\ P=9.75\times 10^{2}\ Pa$

Reynolds number is given by

$\\R=\frac{4\rho V}{\pi d\eta }\\ R=\frac{2\rho V}{\pi r\eta }\\ R=\frac{2\times 1.3\times 10^{3}\times 3.08\times 10^{-6}}{\pi \times 0.01\times 0.83}\\ R\approx 0.3$

Since Reynolds Number is coming out to be 0.3 our Assumption of laminar flow was correct.

Q 10.14 In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s ^-1 and 63 ms ^-1 respectively. What is the lift on the wing if its area is 2.5 m ² ? Take the density of air to be 1.3 kg m ^-3

Answer:

The speed of air above and below the wings are given to be v ₁ = 70 m s ^-1 and v ₂ = 63 m s ^-1 respectively.

Let the pressure above and below the wings be p ₁ and p ₂ and let the model aeroplane be flying at a height h from the ground.

Applying Bernoulli's Principle on two points above and below the wings we get

$\\P_{1}+\rho gh+\frac{1}{2}\rho v_{1}^{2}=P_{2}+\rho gh+\frac{1}{2}\rho v_{2}^{2}\\ P_{2}-P_{1}=\frac{1}{2}\rho (v_{1}^{2}-v_{2}^{2})\\ \Delta P=\frac{1}{2}\times 1.3\times \left ( 70^{2}-63^{2} \right )\\ \Delta P=605.15\ Pa$

The pressure difference between the regions below and above the wing is 605.15 Pa

The lift on the wing is F

$\\F=\Delta P\times Area\ of\ wing\\ F=605.15\times 2.5\\ F=1512.875\ N$

Q 10.15 Figures (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect? Why?

1650445636061

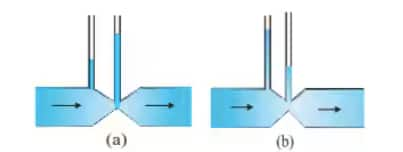
Answer:

By the continuity equation, the velocity of the non-viscous liquid will be large at the kink than at the rest of the tube and therefore pressure would be lesser here by Bernoulli's principle and the air column above it, therefore, should be of lesser height. Figure (a) is therefore incorrect.

Q 10.16 The cylindrical tube of a spray pump has a cross-section of 8.0 cm ² one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min ^-1 , what is the speed of ejection of the liquid through the holes?

Answer:

Cross-sectional area of cylindrical tube is a ₁ = 8.0 cm ²

The total area of the 40 fine holes is a ₂

$\\a_{2}=40\pi (\frac{d^{2}}{4})\\ a_{2}=40\times \pi \times \frac{(10^{-3})^{2}}{4}\\ a_{2}=3.143\times 10^{-5}m^{2}$

Speed of liquid inside the tube is v ₁ = 1.5 m min ^-1

Let the speed of ejection of fluid through the holes be v ₂

Using the continuity equation

$\\a_{1}v_{1}=a_{2}v_{2}\\ v_{2}=\frac{a_{1}v_{1}}{a_{2}}\\ v_{2}=\frac{8\times 10^{-4}\times 1.5}{60\times 3.143\times 10^{-5}}\\ v_{2}=0.636\ m\ s^{-1}$

Q 10.17 A U-shaped wire is dipped in a soap solution, and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10 ^-2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?

Answer:

Total weight supported by the film $W =1.5\times 10^{-2}\ N$

Since a soap film has two surfaces, the total length of the liquid film is 60 cm.

Surface Tension is T

$\\T=\frac{W}{l}\\ T=\frac{1.5\times 10^{-2}}{60\times 10^{-2}}\\ T=2.5\times 10^{-2}\ N\ m^{-1}$

Q 10.18 Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10 ^-2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c) ? Explain your answer physically.

1650445715115

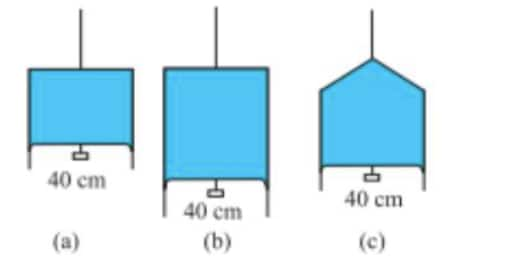
Answer:

As the liquid and the temperature is the same in all three the surface tension will also be the same. Since the length is also given to be equal (40 cm) in all three cases the weight being supported is also the same and equal to $4.5\times 10^{-2}\ N$ .

Q 10.19 What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature? Surface tension of mercury at that temperature (20 °C) is 4.65 × 10 ^-1 N m ^-1 . The atmospheric pressure is 1.01 × 10 ⁵ Pa. Also give the excess pressure inside the drop.

Answer:

Surface Tension of Mercury is $T=4.65\times 10^{-1}\ N\ m^{-1}$

The radius of the drop of Mercury is r = 3.00 mm

Excess pressure inside the Mercury drop is given by

$\\\Delta P=\frac{2T}{r}\\ \Delta P=\frac{2\times 4.65\times 10^{-1}}{3\times 10^{-3}}\\ \Delta P=310\ Pa$

Atmospheric Pressure is $P_{0}=1.01\times 10^{5}\ Pa$

Total Pressure inside the Mercury drop is given by

$\\P_{T}=\Delta P + P_{0}\\ P_{T}=310+1.01\times 10^{5}\\ P_{T}=1.0131\times 10^{5}$

Q 10.20 What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10 ^-2 N m ^-1 ? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 10 ⁵ Pa).

Answer:

Excess pressure inside a bubble is given by

$\Delta P=\frac{4T}{r}$ (It's double the usual value because of the presence of 2 layers in case of soap bubble)

where T is surface tension and r is the radius of the bubble

$\\\Delta P=\frac{4\times 2.5\times 10^{-2}}{5\times 10^{-3}}\\ \Delta P=20\ Pa$

Atmospheric Pressure is $P_{a}=1.01\times 10^{-5}\ Pa$

The density of soap solution is $\rho _{s}=1.2\times 10^{3}\ kg\ m^{-3}$

The pressure at a depth of 40 cm (h) in the soap solution is

$\\P_{s}=P_{a}+\rho _{s}gh\\ P_{s}=1.01\times 10^{5}+1.2\times 10^{3}\times 9.8\times 40\times 10^{-2}\\ P_{s}=1.01\times 10^{5}+4704\\ P_{s}=1.057\times 10^{5}\ Pa$

Total Pressure inside an air bubble at that depth

$\\P_{t}=P_{s}+\frac{2T}{r}\\ P_{t}=1.057\times 10^{5}+\frac{2\times 2.5\times 10^{-2}}{5\times 10^{-3}}\\ P_{t}=1.057\times 10^{5}+10\\ P_{t}=1.0571\times 10^{5}\ Pa$

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids - Additional Exercise

Q 10.21 A tank with a square base of area 1.0 m ² is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20 cm ² . The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to a height of 4.0 m. compute the force necessary to keep the door close

Answer:

Pressure in the waterside at the bottom is

$\\P_{w}=\rho _{w}gh\\ P_{w}=10^{3}\times 9.8\times 4\\ P_{w}=3.92\times 10^{4}$

Pressure in the acid side at the bottom is

$\\P_{a}=\rho _{a}gh\\ P_{w}=1.7\times 10^{3}\times 9.8\times 4\\ P_{w}=6.664\times 10^{4}$

The pressure difference across the door is

$\\\Delta P=P_{a}-P_{w}\\ \Delta P=6.664\times 10^{4}-3.92\times 10^{4}\\ \Delta P=2.774\times 10^{4}\ Pa$

Area of the door, a = 20 cm ²

The force necessary to keep the door closed is

$\\F=a\Delta P\\ F=20\times 10^{-4}\times 2.774\times 10^{4}\\ F=54.88\ N$

Note: The dimensions of the door are small enough to neglect pressure variations near it.

Q 10.22 (a) A manometer reads the pressure of a gas in an enclosure as shown in Figure (a) When a pump removes some of the gas, the manometer reads as in Figure (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.

(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.

Answer: 1650445769597

In figure (a)

Gauge Pressure = 20 cm of Mercury

Absolute Pressure = Atmospheric Pressure + Gauge Pressure

Absolute Pressure = 76 + 20= 96 cm of Mercury

In figure (b)

Gauge Pressure = -18 cm of Mercury

Absolute Pressure = Atmospheric Pressure + Gauge Pressure

Absolute Pressure = 76 + (-18)= 58 cm of Mercury

Q 10.22 (b) A manometer reads the pressure of a gas in an enclosure as shown in Figure (a) When a pump removes some of the gas, the manometer reads as in Figure (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.

(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer?

1650445862863

Answer:

As we know Specific Gravity of Mercury is 13.6 therefore 13.6 cm of water column would be equal to 1 cm of Mercury column.

The pressure at the Mercury Water interface in the right column = Atmospheric Pressure + 1 cm of Mercury = 77 cm of Mercury

The difference in Pressure due to the level of the Mercury column = Pressure at the Mercury Water interface - Absolute Pressure of the Glass enclosure

= 77 - 58 = 19 cm of Mercury.

The difference in the two limbs would, therefore, become 19 cm.

Q 10.23 Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill up to a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?

Answer:

Since the height of the water level in the vessels is the same the Pressure at the bottom would be equal. As the area of the bottom is also the same the Force exerted by the water on the bottom would be the same.

The difference in the reading arises due to the fact that the weight depends on the volume of the water inside the container which is more in the first vessel. The vertical component of the force exerted by the fluid on the sidewalls would be more in the first vessel and the difference in this vertical component is equal to the difference in the readings on a weighing scale.

Q 10.24 During blood transfusion the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein?

Answer:

The density of whole blood $\rho _{w}=1.06\times 10^{3}\ kg\ m^{-3}$

Gauge Pressure $\Delta P=2000\ Pa$

Height at which the blood container must be placed so that blood may just enter the vein

$\\h=\frac{\Delta P}{\rho _{w}g}\\ h=\frac{2000}{1.06\times 10^{3}\times 9.8}\\ h=0.1925\ m$

Q 10.25 (a) In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy.

(a) What is the largest average velocity of blood flow in an artery of diameter 2 × 10–3 m if the flow must remain laminar?

Answer:

The diameter of the artery is $d=2\times 10^{-3}m$

The viscosity of blood is $\eta =2.08\times 10^{-3}\ Pa\ s$

The density of blood is $\rho =1.06\times 10^{3}\ kg\ m^{-3}$

The average velocity is given by $v_{avg}=\frac{N_{Re}\eta }{\rho d}$

Taking the Maximum value of Reynold's Number ( N _Re = 2000) at which Laminar Flow takes place we have

$\\v_{avg,max}=\frac{2000\times 2.08\times 10^{-3}}{1.06\times 10^{3}\times 2\times 10^{-3}}\\ v_{avg,max}=1.97ms^{-1}$

Q 10.25 (b) In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy.

(b) Do the dissipative forces become more important as the fluid velocity increases? Discuss qualitatively.

Answer:

As the fluid velocity increases the dissipative forces become important as turbulence rises due to which drag due to friction forces increases.

Q 10.26 (a) What is the largest average velocity of blood flow in an artery of radius 2×10 ^-3 m if the flow must remain laminar?

Answer:

The diameter of the artery is d

$\\d=2r\\ d=2\times 2\times 10^{-3}\\ d=4\times 10^{-3}$

The viscosity of blood is $\eta =2.08\times 10^{-3}\ Pa\ s$

The density of blood is $\rho =1.06\times 10^{3}\ kg\ m^{-3}$

The average velocity is given by $v_{avg}=\frac{N_{Re}\eta }{\rho d}$

Taking the Maximum value of Reynold's Number ( N _Re = 2000) at which Laminar Flow takes place we have

$\\v_{avg,max}=\frac{2000\times 2.08\times 10^{-3}}{1.06\times 10^{3}\times 4\times 10^{-3}}\\ v_{avg,max}=0.98ms^{-1}$

Q 10.26 (b) What is the corresponding flow rate? (Take viscosity of blood to be 2.084 × 10 ^-3 Pa s).

Answer:

Volumetric flow rate is given as

$\\\frac{dV}{dt}=v_{avg}\pi r^{2}\\ =0.98\times \pi \times (0.02)^{2}\\ =1.235\times 10^{-5}\ m^{3}\ s^{-1}$

Q 10.27 A plane is in level flight at constant speed and each of its two wings has an area of 25 m ² . If the speed of the air is 180 km/h over the lower wing and 234 km/h over the upper wing surface, determine the plane’s mass.

Answer:

Speed of the wind above the upper wing surface is v ₁ = 234 km h ^-1

$\\v_{1}=234\times \frac{1000}{3600}\\v_{1}=65ms^{-1}$

Speed of the wind over the lower wing is v ₂ = 180 km h ^-1

$\\v_{2}=180\times \frac{1000}{3600}\\ v_{2}=50ms^{-1}$

Let the pressure over the upper and lower wing be P ₁ and P ₂

Let the plane be flying at a height of h

The density of air is $\rho =1\ kg\ m^{-3}$

Applying Bernoulli's Principle at two points over the upper and lower wing we get

$\\P_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho gh=P_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho gh\\ P_{2}-P_{1}=\frac{1}{2}\rho (v_{1}^{2}-v_{2}^{2})\\ \Delta P=\frac{1}{2}(65^{2}-50^{2})\\ \Delta P=862.5\ Pa$

Area of each wing is a = 25 m ²

The net upward force on the plane is F

$\\F=2a\Delta P\\ F=2\times 25\times 862.5\\ F=43125\ N$

This upward force is equal to the weight m of the plane.

$\\mg=F\\ m=\frac{F}{g}\\ m=\frac{43125}{9.8}\\ m=4400.51\ kg$

The mass of the plane is about 4400 kg

Q 10.28 In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 × 10 ^-5 m and density 1.2 × 10 ³ kg m ^-3 . Take the viscosity of air at the temperature of the experiment to be 1.8 × 10 ^-5 Pa s. How much is the viscous force on the drop at that speed? Neglect buoyancy of the drop due to air.

Answer:

Neglecting buoyancy due to air the terminal velocity is

$\\v_{T}=\frac{2}{9}\frac{r^{2}\rho g}{\eta }\\ v_{T}=\frac{2\times (2\times 10^{-5})^{2}\times 1.2\times 10^{3}\times 9.8}{9\times 1.8\times 10^{-5}}\\ v_{T}=5.807\times 10^{-2}\ m\ s^{-1}$

Viscous Force F _v at this speed is

$\\F_{v}=6\pi \eta rv_{T}\\ F_{v}=6\pi \times 1.8\times 10^{-5}\times 2\times 10^{-5}\times 5.807\times 10^{-2}\\ F_{v}=3.94\times 10^{-10}N$

Q 10.29 Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m ^-1 . Density of mercury = 13.6 × 10 ³ kg m ^-3 .

Answer:

Since the angle of contact is obtuse the Pressure will be more on the Mercury side.

This pressure difference is given as

$\\\Delta P=\frac{2Tcos(180-\theta )}{r}\\ \Delta P=\frac{2\times 0.465cos40^{o}}{10^{-3}}\\\Delta P=\frac{2\times 0.465\times 0.766}{10^{-3}}\\ \Delta P=712.38\ Pa$

The dip of mercury inside the narrow tube would be equal to this pressure difference

$\\\Delta P=\rho _{Hg}hg\\ h=\frac{\Delta P}{\rho _{Hg}g}\\ h=\frac{712.38}{13.6\times 10^{3}\times 9.8}\\ h=5.34\times 10^{-3}m$

The mercury dips down in the tube relative to the liquid surface outside by an amount of 5.34 mm.

Q 10.30 Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10 ^-2 N m ^-1 . Take the angle of contact to be zero and density of water to be 1.0 × 10 ³ kg m ^-3 (g = 9.8 m s ^-2 ).

Answer:

For the angle of contact $\theta$ , radius of the tube r, surface tension t, the density of fluid $\rho$ the rise in the column is given by

$h=\frac{2Tcos\theta }{r\rho g}$

The radii of the two limbs r ₁ and r ₂ are 3.0 mm and 1.5 mm respectively

The level in the limb of diameter 6.0 mm is

$\\h_{1}=\frac{2Tcos\theta }{r_{1}\rho g}\\ h_{1}=\frac{2\times 7.3\times 10^{-2}cos0^{o}}{3\times 10^{-3}\times 10^{3}\times 9.8}\\h_{1}=4.97\times 10^{-3}m$

The level in the limb of diameter 3.0 mm is

$\\h_{2}=\frac{2Tcos\theta }{r_{2}\rho g}\\ h_{2}=\frac{2\times 7.3\times 10^{-2}cos0^{o}}{1.5\times 10^{-3}\times 10^{3}\times 9.8}\\h_{2}=9.93\times 10^{-3}m$

The difference in the heights is h ₂ - h ₁ = 4.96 mm

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids

Providing class 11 physics chapter 10 exercise solutions is invaluable for Class 11 students, as it aids in their preparation. Additionally, understanding 'Mechanical Properties of Fluids' is crucial for competitive exams like JEE and NEET, where physics plays a significant role. This chapter of mechanical properties of fluids exercise equips students with essential knowledge about fluid behaviour under mechanical forces, helping them tackle complex questions in these exams with confidence.

NCERT Solutions for Class 11 Physics Chapter Wise

Chapter 1	Physical world
Chapter 2	Units and Measurement
Chapter 3	Motion in a straight line
Chapter 4	Motion in a Plane
Chapter 5	Laws of Motion
Chapter 6	Work, Energy and Power
Chapter 7	System of Particles and Rotational motion
Chapter 8	Gravitation
Chapter 9	Mechanical Properties of Solids
Chapter 10	Mechanical Properties of Fluids
Chapter 11	Thermal Properties of Matter
Chapter 12	Thermodynamics
Chapter 13	Kinetic Theory
Chapter 14	Oscillations
Chapter 15	Waves

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Class 11 Physics ch 10 NCERT Solutions: Important Formulas and Diagrams + eBook link

Modulus of rigidity

$Y=\frac{F / A}{\Delta l / l}, B=-V \frac{\Delta P}{\Delta V}, \eta=\frac{F}{A \theta}$

Poisson’s ratio

$\sigma=\frac{\text { lateral strain }}{\text { longitudinal strain }}=\frac{\Delta D / D}{\Delta l / l}$

Elastic energy

U = 1/2*strain*stress*volume

Heat Capacity

Where:

ΔQ is the amount of heat supplied to the substance and ΔT change in its temperature

Specific heat capacity

These formulas are essential because they play a crucial role in solving problems and understanding the concepts covered in Chapter ch 10 physics class 11 ncert solutions.

Mechanical Properties Of Fluids Class 11 NCERT Physics Topics

The problems discussed in the NCERT solutions for Class 11 Physics chapter 10 Mechanical Properties of Fluids are based on the following topics.

10.1 Introduction

10.2 Pressure

10.3 Streamline flow

10.4 Bernoulli’s principle

10.5 Viscosity

10.6 Surface tension

The CBSE is widely recognized as the leading educational board in India, and it follows the NCERT Syllabus to administer examinations for both Class 10 and 12 students. The class 11 physics ch 10 ncert solutions, which focuses on Mechanical Properties of Fluids, have been provided to allow students to gain a comprehensive understanding of the concepts discussed in this chapter.

Fluids possess the fundamental property of being able to flow, and they lack resistance to alterations in their shape. Consequently, the shape of a fluid is determined by the shape of its container. The following are some important points about the Mechanical Properties of Fluids of Matter.

Pressure is a scalar quantity, and although the definition of pressure as "force per unit area" might give the impression that it is a vector, the "force" in the numerator is the component of the force perpendicular to the area on which it is applied.
As the temperature increases, the atoms in a liquid become more mobile, causing the coefficient of viscosity η to decrease. In the case of a gas, the temperature increase results in an increase in the random motion of atoms, which increases η.

Key features of the mechanical properties of fluids exercise solution

Comprehensive Coverage: The ch 10 physics class 11 ncert solutions cover all the topics and concepts presented in the chapter, ensuring a thorough understanding of mechanical properties of fluids.

Step-by-Step Solutions: Detailed step-by-step chapter 10 physics class 11 solutions for each exercise question are provided, making it easy for students to follow and grasp the concepts.

Clarity and Simplicity: The solutions are explained in clear and simple language, making complex concepts easy to understand.

Diagrams and Graphs: Wherever necessary, diagrams and graphs are included to enhance visual understanding and clarify concepts related to fluid properties.

Concise Summaries: NCERT solutions often include concise summaries of the main points in each section, helping students revise and retain important information.

Examination-Oriented: The ch 10 physics class 11 are designed to help students prepare for exams, including CBSE board exams and various competitive exams that may include questions related to fluid mechanics.

Benefits of NCERT solutions for class 11 physics chapter 10 mechanical properties of fluids:

If we are familiar with the CBSE NCERT solutions for Class 11 Physics chapter 10 Mechanical Properties of Fluids then it is very easy to solve problems from other reference books too.
The solutions of NCERT solutions for Class 11 will help to score well in the Class 11 final exam and in competitive exams like JEE Main and NEET also.

NCERT Solutions for Class 11 Subject wise

NCERT solutions for Class 11 Biology

NCERT solutions for Class 11 Maths

NCERT solutions for Class 11 Chemistry

Also Check NCERT Books and NCERT Syllabus here

Subject wise NCERT Exemplar solutions

Frequently Asked Questions (FAQs)

1. Whether the Class 11 chapter Mechanical Properties of Fluids is useful for higher studies

Yes, the topics studied are the basics of fluid dynamics which is mainly studied in mechanical and civil related branches.

2. How many questions are asked from Mechanical Properties of Fluids for NEET and JEE Main

On an average one question is asked from the chapter Mechanical Properties of Fluids for both JEE Main and NEET exam. It can be morethan one also. All the formulas given in the NCERT book for Mechanical Properties of Fluids chapter are important. To get more problems related to the formulas students can use NCERT exemplar and JEE main and NEET previous year papers.

Also Read

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

Hydrogen Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 9 Notes - Download PDF

The S-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 10 Notes - Download PDF

The P-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 11 Notes - Download PDF

Environmental Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 14 Notes - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

NMMS Chhattisgarh Result 2024-25: Check Merit List, Cut Off Marks

Dec 28, 2024

CBSE Scholarship 2024-25: Check CBSE Scholarships for Class 10, 12

Dec 27, 2024

HOS 12th Date Sheet 2025 - Haryana Open School Class 12 Exam Schedule

Dec 27, 2024

AMU School Admission 2025 - Know Application Process, Eligibility & Important Dates

Dec 27, 2024

Jamia Millia Islamia School Application Form 2025 - How to Apply, Eligibility & Important Dates

Dec 27, 2024

TOSS Admission 2024-25: Apply for SSC & Inter TS Open School Admission @telanganaopenschool.org

Dec 27, 2024

DBSE 10th Result 2025 - Check Delhi Board Class 10 Result

Dec 26, 2024

IAPT Cut Off 2024-25 Out, Qualifying Marks for NSEP, NSEC, NSEB, NSEA

Dec 26, 2024

Upcoming School Exams

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Admit Card

Result

National Level Science Talent Search Examination

Answer Key Date:20 December,2024 - 29 December,2024

Exam Pattern

Admit Card

Result

National Institute of Open Schooling 10th examination

Late Fee Application Date:21 December,2024 - 31 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Late Fee Application Date:21 December,2024 - 31 December,2024

Application Process

Exam Pattern

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids

NCERT Solutions Class 11 Physics Chapter 10 – Download Free PDF

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids

Mechanical properties of fluids class 11 NCERT solutions - Exercise

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids - Additional Exercise

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids

Class 11 Physics ch 10 NCERT Solutions: Important Formulas and Diagrams + eBook link

Modulus of rigidity

Poisson’s ratio

Elastic energy

Heat Capacity

Specific heat capacity

Key features of the mechanical properties of fluids exercise solution

Benefits of NCERT solutions for class 11 physics chapter 10 mechanical properties of fluids:

NCERT Solutions for Class 11 Subject wise

Also Check NCERT Books and NCERT Syllabus here

Subject wise NCERT Exemplar solutions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Madhya Pradesh State Open School 10th Examination

Madhya Pradesh State Open School 12th Examination

National Level Science Talent Search Examination

National Institute of Open Schooling 10th examination

National Institute of Open Schooling 12th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app