NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

Edited By Team Careers360 | Updated on Nov 08, 2024 03:34 PM IST

NCERT solutions for class 11 chemistry chapter 5 States of Matter- The matter is existing in 3 physical states which are solid, liquid and gas. In NCERT solutions for class 11 chemistry chapter 5 States of matter, you will deal with the two states of matter namely liquid state and gaseous state, the laws governing the behaviour of ideal gases and properties associated with liquids. In NCERT syllabus class 11 chemistry chapter 5 States of Matter, there are 23 questions in the exercise.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

NEET Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | ALLEN

Also Read :

The NCERT solutions for class 11 chemistry chapter 5 States of Matter are prepared and solved by subject experts. These NCERT solutions will help you in class 11 exam preparation as well as in the preparation of various competitive exams like NEET, JEE, BITSAT etc. By referring to the NCERT solutions for class 11, students can understand all the important concepts and practice questions well enough before their examination.

Some common characteristics of three forms of matter solid liquid and gas are summarised below-

S.No.	Gases	Liquids	Solids
1	No definite shape	No definite shape	Definite shape
2	Indefinite volume	Definite volume	Definite volume
3	Compressible	Slightly compressible	Nearly compressible
4	Low density	Intermediate density	High density

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter- Exercise Questions

Question 5.1 What will be the minimum pressure required to compress $500\; dm^{3}$ of air at 1 bar to $200\; dm^{3}$ at $30^{o}C$ ?

Answer :

Given the volume of air to be compressed is $500dm^3$ at $1 bar$ pressure to $200dm^3$ at $30^{\circ}C$ .

So, as the temperature remains constant at $30^{\circ}C$ .

We have Boyle's law where, $P_{1}V_{1} = P_{2}V_{2}$

To calculate the final pressure $P_{2}$ .

We have,

$P_{1}V_{1} = P_{2}V_{2}$

$P_{2} = \frac{P_{1}V_{1}}{V_{2}}$

$= \frac{1\times 500}{200} bar = 2.5\ bar$

Therefore, the minimum pressure required is $2.5\ bar$ .

Question 5.2 A vessel of $120 \; mL$ capacity contains a certain amount of gas at $35^{o}C$ and 1.2 bar pressure. The gas is transferred to another vessel of volume $180 \; mL$ at $35^{o}C$ . What would be its pressure?

Answer :

Given volume of air to be transferred from the capacity of $120 \; mL$ vessel at $1.2\ bar$ pressure to $180 \; mL$ vessel at 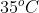$35^{o}C$

So, as the temperature remains constant at 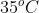$35^{o}C$ .

We have Boyle's law where, $P_{1}V_{1} = P_{2}V_{2}$

To calculate the final pressure $P_{2}$ .

We have,

$P_{1}V_{1} = P_{2}V_{2}$

$P_{2} = \frac{P_{1}V_{1}}{V_{2}}$

$= \frac{1.2\times 120}{180} bar = 0.8\ bar$

Therefore, the pressure required is $0.8\ bar$ .

Question 5.3 Using the equation of state $pV=nRT;$ show that at a given temperature density of a gas is proportional to gas pressure p.

Answer :

Given ideal gas equation ;

$PV = nRT$

So, at given fixed temperature T. we have the

$Density\ of\ gas (\rho ) = \frac{mass(m)}{Volume(V)}$

And we know $n = \frac{Mass\ of\ gas}{Molar\ mass\ of\ gas}$

so, we get $P = \frac{mRT}{MV}$

$P = \frac{\rho RT}{M}$

But at constant Temperature, we have $P \propto \rho$ .

Question 5.4 At $0^{o}\; C$ , the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?

Answer :

Given the condition :

Temperature $= 0^{\circ}C$ ,

$Pressure = 2\ bar$ for oxide gas and $Pressure = 5\ bar$ for dinitrogen.

As Density of gas is represented by, $d = \frac{PM}{RT}$

And given that density is the same for both the gases at the same temperature condition.

So, we have $M_{1}P_{1} = M_{2}P_{2}$ (as R is constant}

or, $M_{1}\times 2 =28\times 5$ $(\because Molecular\ mass\ of\ N_2 = 28\ u)$

or, $M_{1} = 70\ u$

Question 5.5 Pressure of 1 g of an ideal gas A at $27^{o}C$ is found to be 2 bar. When 2 g of another ideal gas B is introduced in the same flask at the same temperature the pressure becomes 3 bar. Find a relationship between their molecular masses.

Answer :

Given Pressure of 1g of an ideal gas A at $27^{\circ}C$ is $P_{A} = 2\ bar$ .

When 2g of another ideal gas B is introduced in the same flask at the same temperature,

The pressure becomes $P_{A}+P_{B}= 3\ bar$ .

$\implies P_{B }= 1\ bar$ .

We can assume the molecular masses of A and B be $M_{A}\ and\ M_{B}$ respectively.

The ideal gas equation, $PV=nRT$

So, we have $P_{A}V=n_{A}RT$ and $P_{B}V=n_{B}RT$

Therefore, $\frac{P_{A}}{P_{B}} = \frac{n_{A}}{n_{B}} = \frac{1M_{B}}{2M_{A}} = \frac{M_{B}}{2M_{A}}$

or, $\frac{M_{B}}{M_{A}} = 2\times\frac{P_{A}}{P_{B}} = 2\times \frac{2}{1} =4$

Hence the relation between the two gases is $M_{B} =4M_{A}$ .

Question 5.6 The drain cleaner, Drainex contains small bits of aluminum which react with caustic soda to produce dihydrogen. What volume of dihydrogen at 20 °C and one bar will be released when 0.15g of aluminum reacts?

Answer :

We have the chemical reaction:

$2 Al +2NaOH +H_2O \rightarrow 2NaAlO_2+3H_{2}$

(Where dihydrogen is being produced.)

So, at $20^{\circ}C$ and $1\ bar$ pressure, the volume of gas that will be released when $0.15g$ of aluminium reacts.

As we can see from the reaction equation that 2 moles of aluminium produce 3 moles of dihydrogen.

i.e., $2\times 27g$ reacts to give $3\times 22.4Litres$

At STP condition

$273.15K$ and $1atm$ ,

$54g(2\times 27g)$ of Al gives $3\times 22400mL$ of $H_{2}$ .

Therefore $0.15g$ of Al will give $= \frac{3\times22400\times0.15}{54}mL$ of $H_{2}$

i.e., $186.67mL$ of $H_{2}$ .

At STP condition:

$273.15K$ and $1atm$ ,

Now, $P_{1} =1atm$ , $V_{1} = 186.67mL$ , $T_{1} = 273.15K$

Then we assume the volume of dihydrogen be $V_{2}$ at the pressure $P_{2} = 0.987atm$

(Since 1 bar = 0.987atm) and temperature $T_{2} = 20^{\circ}C$

$\implies (273.15+20)K = 293.15K$

$\frac{P_{1}V_{1}}{T_{1}} = \frac{P_{2}V_{2}}{T_{2}}$

$V_{2}= \frac{P_{1}V_{1}T_{2}}{P_{2}T_{1}}$

$= \frac{1\times186.67\times293.15}{0.987\times273.15}$

$= 202.98mL\approx 203mL$

Therefore, 203mL of dihydrogen will be released.

Question 5.7 What will be the pressure exerted by a mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a $9\; dm^{3}$ flask at $27 ^{o}C$ ?

Answer :

Given a mixture of 3.2g of methane and 4.4g of carbon dioxide contained a $9dm^3$ flask at $27 ^{o}C$ .

So, the pressure exerted by the mixture will be

$P =\frac{n}{V}RT = \frac{m}{M}\frac{RT}{V}$

The pressure exerted by the Methane gas, $P_{CH_{4}} =(\frac{3.2mol}{16}) \frac{0.0821 dm^3 atm K^{-1}mol^{-1}\times300K}{9 dm^3} = 0.55\ atm$

The pressure exerted by the Carbon dioxide gas,

$P_{CO_{2}} =(\frac{4.4mol}{44}) \frac{0.0821 dm^3 atm K^{-1}mol^{-1}\times300K}{9 dm^3} = 0.27\ atm$

So, the total pressure exerted $= 0.55+0.27 = 0.82\ atm$

And in terms of SI units, we get,

$R = 8.314p\ m^3\ K^{-1}mol^{-1},\ V= 9\times 10^{-3}\ m^3$

$P = 5.543\times10^4 Pa +2.771\times 10^4Pa = 8.314\times10^4 Pa.$

Question 5.8 What will be the pressure of the gaseous mixture when $0.5\: L$ of $H_{2}$ at $0.8$ bar and $2.0\: L$ of dioxygen at $0.7$ bar are introduced in a 1L vessel at $27^{o}C$ ?

Answer :

Pressure of the gas mixture will be the sum of partial pressure of $H_{2}$ gas and partial pressure of $O_{2}$ gas.

So, calculating the partial pressures of each gas.

Partial pressure of $H_{2}$ in a 1L volume vessel.

$P_{1} = 0.8\ bar$ , $P_{2},\ V_{1} = 0.5L,\ V_{2} =1L$

As the temperature remains constant, $P_{1}V_{1} =P_{2}V_{2}$

$\implies (0.8\ bar)(0.5L) = P_{2}(1L)$

or $P_{2} = 0.4\ bar$ or $P_{H_{2}} = 0.4\ bar$

Now, calculating the partial pressure of $O_{2}$ gas in 1L vessel.

$P'_{1}V_{1} = P'_{2} V'_{2}$

$\implies (0.7\ bar)(2L) = P_{2}(1L)$

$\implies P'_{2} = 1.4\ bar$ or $P_{O_{2}} = 1.4\ bar$

Therefore the total pressure $= P_{H_{2}} +P_{O_{2}} = 0.4\ bar+1.4\ bar = 1.8\ bar$

Question 5.9 Density of a gas is found to be $5.46 \: g/dm^{3}$ at $27^{o}C$ at 2 bar pressure. What will be its density at STP ?

Answer :

Given the density of a gas is equal to $5.46g/dm^3$ at $27^{\circ}C$ and at 2bar pressure.

Density $d = \frac{PM}{RT}$ , for the same gas at different temperatures and pressures we can apply,

$\frac{d_{1}}{d_{2}} = \frac{P_{1}}{T_{1}}\times\frac{T_{2}}{P_{2}}.$

Here, 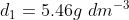$d_{1} =5.46g\ dm^{-3}$ , $T_{1} =27^{\circ}C =300K$ , $P_{1} =2bar.$

then at STP, we have $d_{2},\ T_{2} = 0^{\circ}C =273K,\ P_{2} =1bar.$

$\therefore \frac{5.46g\ dm^{-3}}{d_{2}} = \frac{2bar}{300K}\times\frac{273K}{1bar}$ or $d_{2} = 3g\ dm^{-3}$

Question 5.10 $34.05 \; mL$ of phosphorus vapour weighs 0.0625 g at $546 ^{o}C$ and 0.1 bar pressure. What is the molar mass of phosphorus?

Answer :

Given,

The volume of phosphorus vapour $= 34.05mL$ which weights about $0.0625g$ .

Temperature $= 546^{\circ}C = 273+546 = 819K$

Pressure $=0.1 bar$

Hence we apply the ideal gas equation,

$PV=nRT$ , where the number of moles will be $n =\frac{PV}{RT}$

$= \frac{1bar\times (34.05\times 10^{-3} dm^3)}{0.083 bar\ dm^3\ K^{-1}Mol^{-1}\times 819K}$

$= 5\times 10^{-4} mol$

$\therefore Mass\ of\ 1\ mole = \frac{0.0625}{5\times 10^{-4}}g = 125g$

Therefore the molar mass is $125g\ mol^{-1}$

Question 5.11 A student forgot to add the reaction mixture to the round bottomed flask at 27 °C but instead he/she placed the flask on the flame. After a lapse of time, he realized his mistake, and using a pyrometer he found the temperature of the flask was 477 °C. What fraction of air would have been expelled out?

Answer :

Assume the round-bottomed flask has volume $= V\ cm^3$

so, the volume of air in the flask at $27^{\circ}C$ $= V\ cm^3$ .

To find out how much air has been expelled out, we use Charle's Law:

$\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}$

Therefore $Volume\ expelled = 2.5V-V =1.5V$

Or, Fraction of air expelled $=\frac{1.5V}{2.5V} =\frac{3}{5}$

Question 5.12 Calculate the temperature of $4.0 \: mol$ of a gas occupying $5\: \: dm^{3}$ at 3.32 bar.
$(R = 0.083 \: bar\: dm^{3} K^{-1} mol^{-1}).$

Answer :

We have the ideal gas equation,

$PV=nRT$

Pressure, p=3.32bar

Volume, V=5 $dm^3$

Number of moles, n=4 mol

Gas constant R= 0.083

Temperature, T=?

$T = \frac{PV}{nR} = \frac{3.32bar\times 5\ dm^3}{4\ mol\times 0.083 bar\ dm^3\ K^{-1}mol^{-1}} = 50K$

so, temperature, T=50K

Question 5.13 Calculate the total number of electrons present in 1.4 g of dinitrogen gas.

Answer :

Dinitrogen $N_{2}$ has a molar mass $= 28g\ mol^{-1}$ .

Given 1.4g of $N_{2}$ gas.

That means $\frac{1.4}{28} = 0.05\ mol$

$= 0.05\times6.02\times10^{23} = 3.01\times 10^{23}$ number of molecules.

And as 1 molecule of $N_{2}$ has 14 electrons.

So, $3.01\times 10^{23}$ molecules of $N_{2}$ has $14\times 3.01\times 1023 = 4.214\times 10^{23}$ electrons.

Question 5.14 How much time would it take to distribute one Avogadro number of wheat grains, if 1010 grains are distributed each second ?

Answer :

Given that $10^{10}$ grains are distributed each second.

Time taken to distribute $10^{10}$ grains = 1second.

Time taken to distribute one Avogadro number of wheat grains.

$=\frac{1s\times 6.022\times 10^{23}grains}{10^{10}grains}$

$= \frac{6.022\times10^{23}}{60\times 60\times 24\times 365} = 1.9\times 10^{6}\ years.$

Question 5.15 Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of $1\: dm^{3}$ at 27°C. $R = 0.083\: bar \: dm^{3} K^{-1} mol^{-1}$ .

Answer :

Given the mass of oxygen gas and mass of hydrogen gas.

Molar mass of $O_{2} =32g\ mol^{-1}$

Therefore $8g\ O_{2} = \frac{8}{32}mol = 0.25\ mol$

Molar mass of $H_{2} = 2g\ mol^{-1}$

Therefore $4g H_{2} =\frac{4}{2} =2\ mol$

$\Rightarrow$ Total number of moles of mixture $n = 2+0.25 =2.25$

and $V = 1\ dm^3,\ T = 27^{\circ }C = 300K,\ R=0.083\ bar\ dm^{3}K^{-1}\ mol^{-1}$

So, Ideal gas equation; $PV = nRT$

or $P = \frac{nRT}{V} = \frac{(2.25mol\times) (0.083 bar\ dm^3K^{-1}mol^{-1})(300K)}{1 dm^3}$

Therefore Total pressure is $= 56.025\ bar$

Question 5.16 Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius 10 m, mass 100 kg is filled with helium at 1.66 bar at 27°C.

(Density of $air = 1.2 \: kg\: m^{-3}$ and $R = 0.083 \: bar \: dm^{3} K^{-1} mol^{-1}$ ).

Answer :

The payload can be defined as:

(Mass of the displaced air - Mass of the balloon)

Given the radius of the balloon, r = 10 m.

Mass of the balloon, m = 100 kg.

Therefore, the volume of the balloon will be:

$V = \frac{4}{3}\pi r^3 = \frac{4}{3}\times\frac{22}{7}\times10^3 = 4190.5\ m^3$

Now, the volume of the air displaced:

$V_{d} = 4190.5\ m^3$

The mass of the air displaced :

$m_{d} = density \times V_{d} = 1.2kgm^{-3}\times 4190.5\ m^3$

$= 5028.6kg$

Let $W$ be the mass of helium gas filled into the balloon, then

$PV=(\frac{W}{m})rt$

Or, $W = \frac{PVM}{RT}$

$= \frac{1.66\times4190.5\times10^3\times4}{0.083\times300} = 1117\ kg$ approximately.

The balloon is filled with He with total mass of $= 1117+100= 1217kg$

$\therefore$ The payload of the balloon will be:

$= 5028.6 -1217 = 3811.6kg$

Question 5.17 Calculate the volume occupied by 8.8 g of $CO_{2}$ at 31.1°C and 1 bar pressure. $R = 0.083 \: bar \: L\: K^{-1} mol^{-1}$ .

Answer :

Given the mass of carbon dioxide is 8.8grams at $31.1^{\circ}C$ and at 1 bar pressure.

So, the number of moles of

$CO_{2} (n) = \frac{Mass\ of\ CO_{2}}{Molar\ Mass}$

$= \frac{8.8g}{44g\ mol^{-1}} = 0.2\ mol$

Now, the pressure of $CO_{2} (P) = 1\ bar$

Given $R = 0.083 \: bar \: L\: K^{-1} mol^{-1}$

also, the $Temperature (T) = 273+31.1 = 304.1K$

The Ideal gas equation; $PV=nRT$

$V=\frac{nRT}{P} = \frac{0.2\times 0.083\times304.1}{1\ bar} = 5.048L$

So volume occupied by 8.8 g of carbon dioxide is 5.048L

Question 5.18 2.9 g of a gas at 95 °C occupied the same volume as 0.184 g of dihydrogen at 17 °C, at the same pressure. What is the molar mass of the gas?

Answer :

Let the molar mass of the gas be $M_{gas}$ ,

Then, given that $2.9g$ of a gas at $95^{\circ}C$ occupied the same volume as

$0.184g$ of $H_{2}$ at $17^{\circ }C$

So, we have the relation, $P_{1}=P_{2}$ and $V_{1} = V_{2}$

Therefore $P_{1}V_{2} = P_{2} V_{2}$

wihch gives, $n_{1}RT_{1} =n_{2}RT_{2}$

$\implies n_{1}T_{1} =n_{2}T_{2}$

Or, $\frac{2.9}{M_{gas}}\times (95+273) = \frac{0.184}{2}\times(17+273)$

Or, $M_{gas} = \frac{2.9\times368\times 2 }{0.184\times 290} = 40g\ mol^{-1}$

Question 5.19 A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrogen.

Answer :

A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen.

So, let us assume the weight of dihydrogen in a total mixture weight of $W$ be $20Wgrams$ and dioxygen be $80Wgrams$ .

Then, the number of moles of $H_{2}$ will be, $n_{H_{2}} = \frac{20W}{2} = 10W\ moles$ and the number of moles of $O_{2}$ , $n_{O_{2}} = \frac{80W}{32} = 2.5W\ moles$ .

And given that the total pressure of the mixture is $P_{Total} = 1\ bar$ .

Then we have a partial pressure of $H_{2}$ ,

$P_{H_{2}}=(Mol.\ fraction)_{H_{2}}\times P_{Total}$

$= \frac{n_{H_{2}}}{n_{H_{2}}+n_{O_{2}}}\times P_{Total}$

$= \frac{10W}{10W+2.5W}\times 1\ bar$

$=0.8\ bar$

Therefore, the partial pressure of $H_{2}$ is $0.8\ bar$ .

Question 5.20 What would be the $SI$ unit for the quantity $pV^{2}T^{2}/n$ ?

Answer :

Given quantity, $pV^{2}T^{2}/n$ ,

The SI units of each factors are,

For pressure p is $Nm^{-2}$ .

For Volume V is $m^3$ .

For Temperaute T is $K$ .

For number of moles, n is mol.

Therefore we have for the quantity

The SI unit is $=\frac{(Nm^{-2})(m^3)^2)(K)^2}{mol}$

$= Nm^4K^2 mol^{-1}$

Question 5.21 In terms of Charles’ law explain why –273 °C is the lowest possible temperature.

Answer :

Charles' Law states that pressure remaining constant, the volume of a fixed mass of a gas is directly proportional to its absolute temperature.

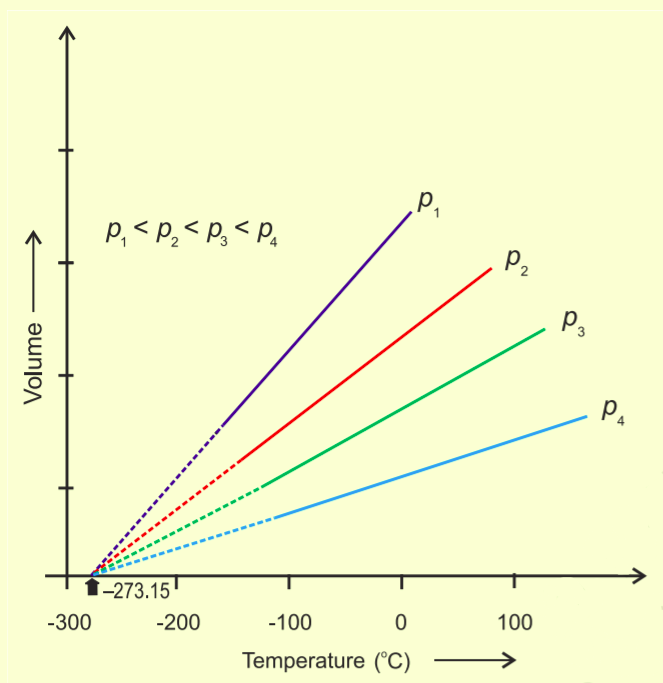
1650521155405

Charles found that for all gases, at any given pressure, the graph of volume vs temperature (in Celsius) is a straight line and on extending to zero volume, each line intercepts the temperature axis at – 273.15 ° C.

We can see that the volume of the gas at – 273.15 ° C will be zero. This means that gas will not exist. In fact, all the gases get liquified before this temperature is reached.

Question 5.22 Critical temperature for carbon dioxide and methane are 31.1 °C and –81.9 °C respectively. Which of these has stronger intermolecular forces and why?

Answer :

The critical temperature we know is the highest temperature at which liquid exists above it is gas.

Given that the critical temperature of Carbon dioxide and Methane are. $31.1 ^{\circ}C\ and\ -81.9^{\circ}C$

Higher is the critical temperature of a gas, easier is its liquefaction.

So, as the critical temperature increases the gas is now easier to liquefaction.

That means the intermolecular forces of attraction between the molecules of a gas are directly proportional to its Critical temperature.

Hence, Carbon dioxide has stronger intermolecular forces than Methane.

Question 5.23 Explain the physical significance of van der Waals parameters.

Answer :

The equation of van der Waals after taking into account the corrections for pressure and volume,

$\left ( p+\frac{an^2}{V^2} \right )\left ( V-nb \right ) =nRT$

Where a and b are called van der Waals constants or parameters.

Here the significance of a and b is important:

Value of ' a' is a measure of the magnitude of intermolecular attractive forces within the gas and is independent of temperature and pressure.

And the value of 'b' is the volume occupied by the molecule and 'nb' is the total volume occupied by the molecules.

More About NCERT Solutions For States Of Matter Class 11 Chemistry

NCERT solutions for class 11 chemistry chapter 5 States of Matter is an important chapter for class 11 students because the topics of this chapter are the basics to the topics to be studied in class 12 NCERT book. The important topics of this chapter are intermolecular forces, thermal energy, the gaseous state, ideal gas equation, kinetic molecular theory of gases, liquid State and more. After completing the NCERT solutions for class 11 chemistry chapter 5 states of matter students will be able to explain the existence of different states of matter, explain the laws governing the behaviour of ideal gases; able to apply gas laws in real life situations; describe the conditions required for liquefaction of gases and also able to differentiate between vapours and gaseous state.

NCERT Solutions for Class 11 Chemistry

Chapter 1	Some Basic Concepts of Chemistry
Chapter-2	Structure of Atom
Chapter-3	Classification of Elements and Periodicity in Properties
Chapter-4	Chemical Bonding and Molecular Structure
Chapter-5	States of Matter
Chapter-6	Thermodynamics
Chapter-7	Equilibrium
Chapter-8	Redox Reaction
Chapter-9	Hydrogen
Chapter-10	The S-Block Elements
Chapter-11	The P-Block Elements
Chapter-12	Organic chemistry- some basic principles and techniques
Chapter-13	Hydrocarbons
Chapter-14	Environmental Chemistry

NCERT Solutions for Class 11 Subject Wise

NCERT solutions for Class 11 Biology

NCERT Solutions for Class 11 Maths

NCERT solutions for Class 11 Chemistry

NCERT solutions for Class 11 Physics

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Benefits of NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

The solutions are written in a comprehensive manner in the NCERT solutions for class 11 chemistry chapter 5 States of Matter will help you writing answers in your exam.
Revision will be easy because the detailed solutions will help you to remember the concepts and get you good marks.
Homework problems will be easier for you, all you need to do is check the detailed NCERT solutions for class 11 chemistry and you are ready to go.

If you have a doubt or question that is not available here or in any of the chapters, contact us. You will get all the answers that will help you score well in your exams.

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Questions (FAQs)

1. What is the weightage of states of matter in JEE Mains

This chapter holds weightage of 7 marks in JEE mains

2. Where can I find complete solutions of NCERT class 11 Chemistry

Refer to this link: https://school.careers360.com/ncert/ncert-solutions-class-11-chemistry

3. How are the ncert solutions beneficial for board exam

Most of the questions are asked directly from NCERT, hence it is must to do ncert solutions

4. Whether the unit states of matter is helpful in higher studies?

Yes, it is helpful to a large extent

5. What is the weightage of the chapter states of matter for CBSE board exam

5 marks

6. What is the weightage of NCERT chapter states of matter for NEET exam

This chapter holds weightage of 2%

Also Read

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

Hydrogen Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 9 Notes - Download PDF

The S-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 10 Notes - Download PDF

The P-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 11 Notes - Download PDF

Environmental Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 14 Notes - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 16, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter- Exercise Questions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Means Cum-Merit Scholarship

Gujarat Board Higher Secondary School Certificate

Madhya Pradesh State Open School 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app