NCERT Exemplar Class 12 Physics Solutions Chapter 1 Electric Charges and Fields
Have you ever heard a crackling sound, or a little spark, as you pull a wool sweater off in dark room? That is static electricity at work. It is that type of real life activity which is an ideal introduction to the notions in Chapter 1 of Physics in Class 12 Electric Charges and Fields. The chapter develops your knowledge in introduction to such basic concepts as static electric charges, electric fields, electric forces, and others.To enable the students to explore these concepts further, NCERT Exemplar Solutions Class 12 Physics Chapter 1 acts as a one-stop solution in creating a clearer understanding of the concepts and better solution ability towards problems.
A score of 87.5 in JEE Main is considered above average, but whether it is “good” depends on the context. In percentile terms, 87.5 marks usually correspond to a high percentile, but it may not be enough for admission to top NITs or IITs, which generally require higher scores. For admission to state-level colleges, private engineering colleges, or less competitive NIT branches, it is likely to be sufficient.
This Story also Contains
- NCERT Exemplar Class 12 Physics Solutions Chapter 1 MCQI
- NCERT Exemplar Class 12 Physics Solutions Chapter 1 MCQII
- NCERT Exemplar Class 12 Physics Solutions Chapter 1 Very Short Answer
- NCERT Exemplar Class 12 Physics Solutions Chapter 1 Short Answer
- NCERT Exemplar Class 12 Physics Solutions Chapter 1 Long Answer
- NCERT Exemplar Class 12 Physics Chapter Wise Links

The solutions are carefully developed by the experts in the subject who have analyzed the textbook and exemplar problems thoroughly. The various types of questions provided by the NCERT Exemplar are multiple choice questions (MCQs), short answer question, long answer question, and very long answer question and thus provides students with a lot of practice and preparation regarding the board exams and also the competitive exams like JEE and NEET. These solutions act as reliable source of reference to revise even better and a source of knowledge as to comprehend the practical uses of electrostatics.
NCERT Exemplar Class 12 Physics Solutions Chapter 1 MCQI
Question:1.1
In Fig.1.1, two positive charges q2 and q3 fixed along the y axis, exert a net electric force in the + x direction on a charge q1 fixed along the x axis. If a positive charge Q is added at (x, 0), the force on q1
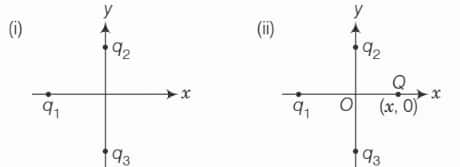
A. shall increase along the positive x-axis.
B. shall decrease along the positive x-axis.
C. shall point along the negative x-axis.
D. shall increase but the direction changes because of the intersection of Q with q2 and q3.
Answer:
The answer is the option (a)The net force on $q_1$ by $q_2$ and $q_3$ is along the $+x$-direction, so nature of force between $q_1, q_2$ and $q_1, q_3$ is attractive. This can be represent by the figure given below
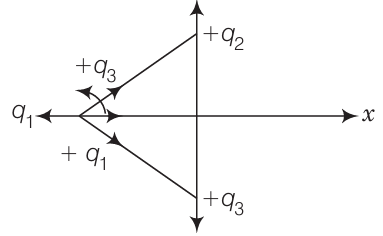
The attractive force between these charges states that $q_1$ is a negative charge (since, $q_2$ and $q_3$ are positive).
Thus, nature of force between $q_1$ and newly introduced charge $Q$ (positive) is attractive and net force on $q_1$ by $q_2, q_3$ and $Q$ are along the same direction as given in the diagram below
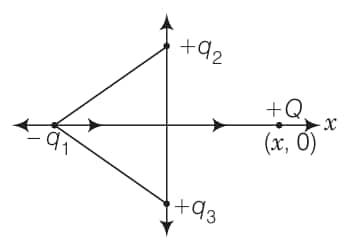
The figure given above clearly shows that the force on $q_1$ shall increase along the positive $x$-axis due to the positive charge $Q$.
Question:1.2
A point positive charge is brought near an isolated conducting sphere (Fig. 1.2). The electric field is best given by
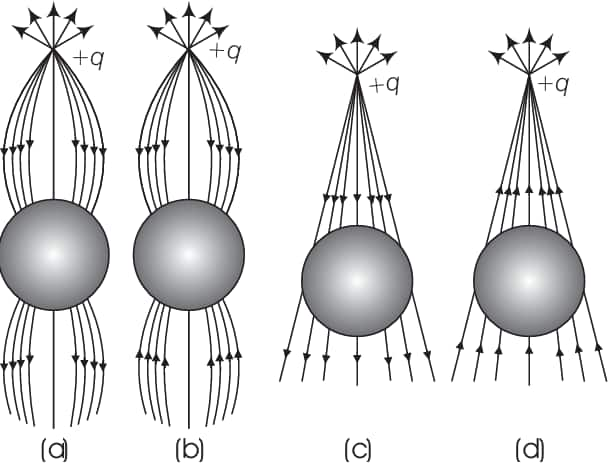
A. Fig (a)
B. Fig (b)
C. Fig (c)
D. Fig (d)
Answer:
The answer is the option (a)Explanation: The electric field lines are always perpendicular to the conducting surface. There are no lines inside the conducting surface, and the electric field lines are always coming out of positive charge and goes into a negative charge. Therefore (a) is the correct answer.
Question:1.3
The electric flux through the surface
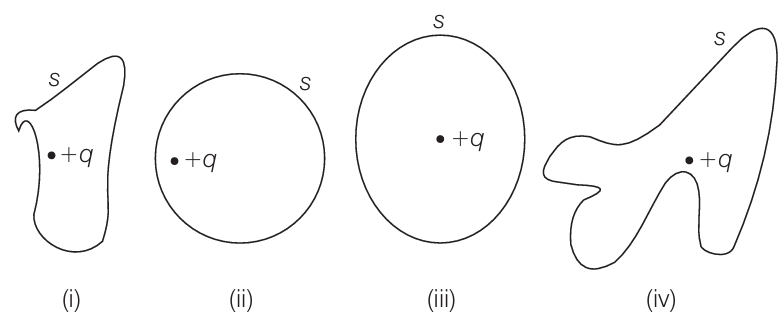
A. in fig. (iv) is the largest
B. in fig. (iii) the least
C. in fig (ii) is same as (iii) but samaller han (iv)
D. is same for all figure
Answer:
Answer: The answer is the option (d)Explanation: According to Gauss' theorem, the total electric flux out of an enclosed area is equal to charge enclosed divided by permittivity.
Here all the areas are equal; therefore, the equal flux will pass through all of them. Hence, (d) is correct.
Question:1.4
Five charges q1, q2, q3, q4, and q5 are fixed at their positions, as shown in Fig. 1.4. S is a Gaussian surface. Gauss's law is given by
$\oint_{s} E.ds=\frac{q}{\varepsilon _0}$ Which of the following statements is correct?

A. E on the LHS of the above equation will have a contribution from q1, q5 and q3 while q on the RHS will have a contribution from q2 and q4 only.
B. E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only.
C. E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q1, q3 and q5 only.
D. Both E on the LHS and q on the RHS will have contributions from q2 and q4 only..
Answer:
The answer is the option (b)
According to Gauss' law, the term $q$ on the right side of the equation $\int_S E . d S=\frac{q}{\varepsilon_0}$ includes the sum of all charges enclosed by the surface.
The charges may be located anywhere inside the surface, if the surface is so chosen that there are some charges inside and some outside, the electric field on the left side of equation is due to all the charges, both inside and outside $S$.
So, $E$ on LHS of the above equation will have a contribution from all charges while $q$ on the RHS will have a contribution from $q_2$ and $q_4$ only.
Question:1.5
Figure 1.5 shows electric field lines in which an electric dipole p is placed as shown. Which of the following statements is correct ?

A. The dipole will not experience any force.
B.The dipole will experience a force towards right.
C.The dipole will experience a force towards left.
D.The dipole will experience a force upwards.
Answer:
The answer is the option (c)Explanation: Here, the electric field lines are non-uniform, and their strength decreases from left to right. Therefore, the force on -q is more than +q. So, the dipole will experience a force towards the left.
Question:1.6
A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
A. directed perpendicular to the plane and away from the plane.
B. directed perpendicular to the plane but towards the plane.
C. directed radially away from the point charge.
D. directed radially towards the point charge.
Answer:
The answer is the option (a)Explanation: The electric field lines are always parallel to the conducting plane; therefore, the lines here will be and directing away from the plane. There are no conducting lines inside the conductor. Hence, (a) is correct.
Question:1.7
A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed.
A. perpendicular to the diameter
B. parallel to diameter
C. at an angle tilted towards the diameter
D. at an angle tilted away towards the diameter
Answer:
The answer is the option (a)
Explanation: In a uniformly positively charged hemisphere, the electric field should be perpendicular on a point away from the center towards the diameter.NCERT Exemplar Class 12 Physics Solutions Chapter 1 MCQII
Question:1.8
If $\oint _{s} Eds =0$ over a surface, then
A. The electric field inside the surface and on it is zero.
B. The electric field inside the surface is necessarily uniform.
C. The number of flux lines entering the surface must be equal to the number of flux lines leaving it
D. All charge must necessarily be outside the surface.
Answer:
The correct answers are the options (c,d)Explanation: $\phi _{s}= 0$ represents that number of electric field lines entering an area is equal to the number of electric field lines leaving. And also, here $q=0$; therefore the charge must be outside the enclosed area.
Question:1.9
The Electric field at a point is
A. always continuous.
B. continuous if there is no charge at that point.
C. discontinuous only if there is negative charge at that point.
D. discontinuous if there is a charge at that point.
Answer:
The correct answers are the options (b,d)Explanation: Electric field lines cannot be defined at a point where a charge is present. While at any point electric field will be continuous if only one charge is present in the medium.
Question:1.10
If there were only one type of charge in the universe, then
A. $\oint_{s}E.ds\neq 0$ on any surface
B. $\oint_{s}E.ds= 0$ if the charge is outside the surface.
C. $\oint_{s}E.ds$could not be defined.
D.$\oint_{s}E.ds= \frac{q}{\varepsilon _0}$ if charge of magnitude q were inside the surface.
Answer:
The correct answers are the options (b,d)Explanation:$\phi _{s}= \oint_{s}E . dS= \frac{q}{\varepsilon _0}$ from Gauss' law. Therefore, if $\phi _{s}=\oint_{s}E . dS= 0$ then $q=0$, therefore the net enclosed charge should be 0. And if the charge is outside the surface then also $q=0$. Therefore, (b,d) are correct.
Question:1.11
Consider a region inside which there are various types of charges, but the total charge is zero. At points outside the region
A. The electric field is necessarily zero.
B. The electric field is due to the dipole moment of the charge distribution only.
C. The dominant electric field is $\alpha \frac{1}{r^3}$, for large r, where r is the distance from an origin in this region.
D. The work done to move a charged particle along a closed path, away from the region, will be zero.
Answer:
The correct answers are the options (c,d)Explanation: There are charges present inside the surface, and their sum is zero. In equation
$\phi = \oint_{s} E.dS=\frac{q}{\varepsilon _0}$
E is the electric field due to all the charges present in and out of the gaussian surface. Therefore, there must be dipoles present inside the surface.
So, at any point outside the region w.r.t the dipoles inside the region the dominant electric field $\alpha \frac{1}{r^3}$ for large r.
Also, the electric field is conservative, and work done to move a charge on a closed path away from the region will be zero. Here c and d are correct.
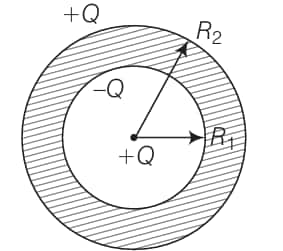
Question:1.12
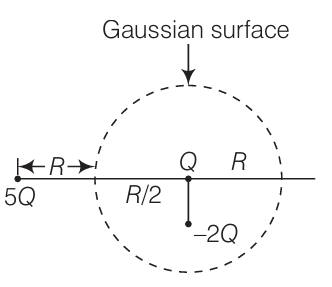
Fig 1.6
A. total flux through the surface of the sphere is $\frac{-Q}{\varepsilon _0}$
B. field on the surface of the sphere is $\frac{-Q}{4\pi \varepsilon _0R^{2}}$.
C. flux through the surface of sphere due to 5Q is zero.
D. field on the surface of sphere due to –2Q is same everywhere.
Answer:
The correct answers are the options (a,c)Explanation: 5Q charge lies outside the Gaussian surface, hence making no contribution to the electric flux. So, a and c are correct options.
Question:1.13
Fig 1.7
A. If q > 0 and is displaced away from the centre in the plane of the ring, it will be pushed back towards the centre.
B. If q < 0 and is displaced away from the centre in the plane of the ring, it will never return to the centre and will continue moving till it hits the ring.
C. If q < 0, it will perform SHM for small displacement along the axis.
D. q at the centre of the ring is in an unstable equilibrium within the plane of the ring for q > 0.
Answer:
Answer: The correct answers are the options (a, b, d)Explanation: As the positive charge is uniformly distributed over the ring, the charge at the centre will be zero. So, no force is exerted on charge at the centre. If the charge is pushed away from the centre, it will experience a force pushing back towards the centre, and if the charge is negative, then it will experience a force towards the ring circumference. Also, the negative charge will be in an unstable equilibrium. So, options a, b, and d are correct.
NCERT Exemplar Class 12 Physics Solutions Chapter 1 Very Short Answer
Question:1.14
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
Answer:
According to Gauss' law
$\phi _s=\int E . dS =\frac{q}{\varepsilon _0}$
where q= enclosed charge. So, +q and -q will cancel each other in a dipole and the sum of the charges will be zero.
Question:1.15
Answer:
Here, the charge placed at the centre of the spherical cavity is positively charged. So, the charge created at the inner surface of the sphere, due to induction will be $-Q$ and due to this charge created at outer surface of the sphere is $+Q$.
The surface density is denoted by σ.
a) The surface charge density on the inner surface is σ1= charge/ Area = $\frac{-Q}{4\pi R_{2}^{1}}$
b) The surface charge density on the other surface is σ2= $\frac{+Q}{4\pi R_{2}^{2}}$
Question:1.16
Answer:
Answer: The protons and electrons are bound into a atom with distinct and independent existence and neutral in charge. Electrostatic fields are caused by the presence of excess charges. But there can be no excess charge on the inter surface of an isolated conductor. So, the electrostatic fields inside a conductor is zero despite the fact that the dimensions of an atom are of the order of an Angstrom.Question:1.17
Answer:
If the total charge is zero enclosed by a surface, it does not necessarily mean that the electric field is also zero enclosed by the surface. The electric field can be perpendicular to the surface. While conversely, it does imply that the electric field is zero on the surface.Question:1.18
Sketch the electric field lines for a uniformly charged hollow cylinder shown in Fig 1.8.
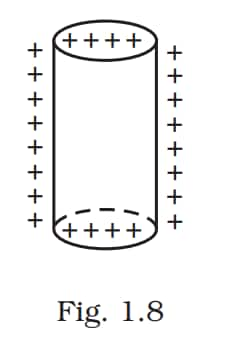
Answer:
The side view and the top view of the electric field lines for a uniformly charged hollow cylinder are given below: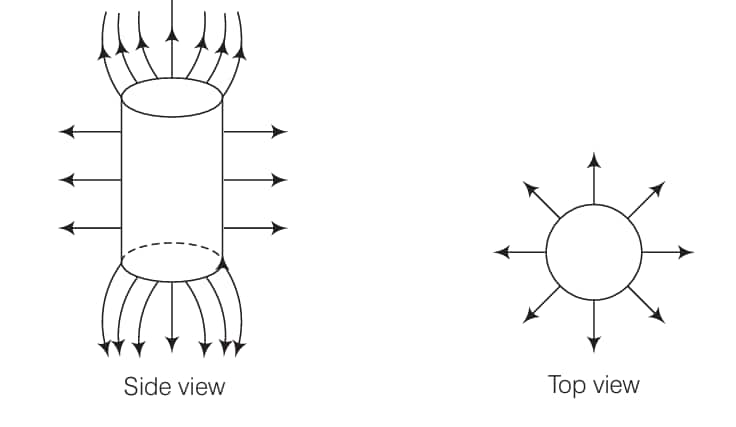
Question:1.19

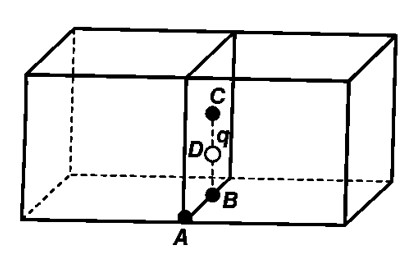
(a) A: a corner of the cube.
(b) B: mid-point of an edge of the cube.
(c) C: centre of a face of the cube.
(d) D: mid-point of B and C.
Answer:
a) The charge is equally distributed amongst the 8 cubes of a divided cube with sides 2a when the charge is placed at the center of the large cube. Therefore, the total flux through the faces of the cube$= \frac{q}{8\varepsilon _0}$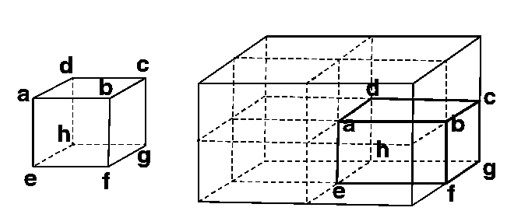
b) If the charge is placed at B, it is equally distributed amongst the 4 cubes. Hence, the total flux through the four faces is $= \frac{q}{4\varepsilon _0}$
c) If the charge is placed at C, then the charge is share by 2 cubes equally, therefore the total flux will be$= \frac{q}{2\varepsilon _0}$
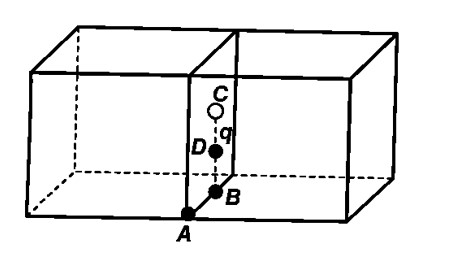
d) If the charge is placed at D, it is distributed amongst two cubes and therefore, the flux through them will be$= \frac{q}{2\varepsilon _0}$
NCERT Exemplar Class 12 Physics Solutions Chapter 1 Short Answer
Question:1.20
Answer:
Here, given quantities are
Mass of a paisa coin $=0.75 \mathrm{~g}$
Atomic mass of aluminium $=26.9815 \mathrm{~g}$
Avogadro's number $=6.023 \times 10^{23}$
$\therefore \quad$ Number of aluminium atoms in one paisa coin,
$
N=\frac{6.023 \times 10^{23}}{26.9815} \times 0.75=1.6742 \times 10^{22}
$
As charge number of Al is 13 , each atom of Al contains 13 protons and 13 electrons.
$\therefore \quad$ Magnitude of positive and negative charges in one paisa coin $=NZe$
$
\begin{aligned}
& =1.6742 \times 10^{22} \times 13 \times 1.60 \times 10^{-19} \mathrm{C} \\
& =3.48 \times 10^4 \mathrm{C}=34.8 \mathrm{kC}
\end{aligned}
$
This is a very large amount of charge. Thus, we can conclude that ordinary neutral matter contains enormous amount of $\pm$ charges.
Question:1.21
Answer:
$\begin{aligned} & q= \pm 34.8 \mathrm{RC}= \pm 3.48 \times 10^4 \mathrm{C} \\ & r_1=1 \mathrm{~cm}=10^{-2} \mathrm{~m}, r_2=100 \mathrm{~m}, r_3=10^6 \mathrm{~m} \text { and } \frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \\ & F_1=\frac{|q|^2}{4 \pi \varepsilon_0 r_1^2}=\frac{9 \times 10^9\left(3.48 \times 10^4\right)^2}{\left(10^{-2}\right)^2}=1.09 \times 10^{23} \mathrm{~N} \\ & F_2=\frac{|q|^2}{4 \pi \varepsilon_0 r_2^2}=\frac{9 \times 10^9\left(3.48 \times 10^4\right)^2}{(100)^2}=1.09 \times 10^{15} \mathrm{~N} \\ & F_3=\frac{|q|^2}{4 \pi \varepsilon_0 r_3^2}=\frac{9 \times 10^9\left(3.48 \times 10^4\right)^2}{\left(10^6\right)^2}=1.09 \times 10^7 \mathrm{~N}\end{aligned}$
Conclusion from this result We observe that when $\pm$ charges in ordinary neutral matter are separated as point charges, they exert an enormous force. Hence, it is very difficult to disturb electrical neutrality of matter.
Question:1.22
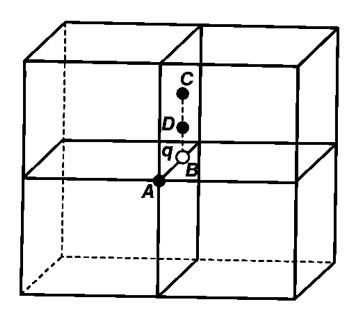
Fig. 1.10 represents a crystal unit of cesium chloride, CsCl. The cesium atoms, represented by open circles are situated at the corners of a cube of side 0.40nm, whereas a Cl atom is situated at the centre of the cube. The Cs atoms are deficient in one electron while the Cl atom carries an excess electron.

(i) What is the net electric field on the Cl atom due to eight Cs atoms?
(ii) Suppose that the Cs atom at the corner A is missing. What is the net force now on the Cl atom due to seven remaining Cs atoms?
Answer:
(i) From the given figure, we can analyse that the chlorine atom is at the centre of the cube i.e., at equal distance from all the eight corners of cube where cesium atoms are placed. Thus, due to symmetry the forces due to all Cs tons, on Cl atom will cancel out.
Hence,
$
\begin{aligned}
& E=\frac{F}{q} \text { where } F=0 \\
& E=0
\end{aligned}
$
(ii) Thus, net force on Cl atom at $A$ would be,
$
F=\frac{e^2}{4 \pi \varepsilon_0 r^2}
$
where, $\quad r=$ distance between Cl ion and Cs ion.
Applying Pythagorous theorem, we get
Now,
$
\begin{aligned}
r & =\sqrt{(0.20)^2+(0.20)^2+(0.20)^2} \times 10^{-9} \mathrm{~m} \\
& =0.346 \times 10^{-9} \mathrm{~m} \\
F & =\frac{q^2}{4 \pi \varepsilon_0 r^2}=\frac{e^2}{4 \pi \varepsilon_0 r_2} \\
& =\frac{9 \times 10^9\left(1.6 \times 10^{-19}\right)^2}{\left(0.346 \times 10^{-9}\right)^2}=1.92 \times 10^{-9} \mathrm{~N}
\end{aligned}
$
Question:1.23
Answer:
\text { Here, let us keep the charge } 2 q \text { at a distance } r \text { from } A \text {. }

Thus, charge $2 q$ will not experience any force.
When, force of repulsion on it due to $q$ is balanced by force of attraction on it due to $-3 q$, at $B$, where $A B=d$.
Thus, force of attraction by $-3 q=$ Force of repulsion by $q$
$
\begin{aligned}
& \Rightarrow & \frac{2 q \times q}{4 \pi \varepsilon_0 x^2} & =\frac{2 q \times 3 q}{4 \pi \varepsilon_0(x+d)^2} \\
& \Rightarrow & (x+d)^2 & =3 x^2 \\
& \Rightarrow & x^2+d^2+2 x d & =3 x^2 \\
\end{aligned}
$
$
\therefore \quad \begin{aligned}
2 x^2-2 d x-d^2 & =0 \\
x & =\frac{d}{2} \pm \frac{\sqrt{3} d}{2}
\end{aligned}
$
(Negative sign be between $q$ and $-3 q$ and hence is unadaptable.)
$
\begin{aligned}
x & =-\frac{d}{2}+\frac{\sqrt{3} d}{2} \\
& =\frac{d}{2}(1+\sqrt{3}) \text { to the left of } q .
\end{aligned}
$
Question:1.24
Fig. 1.11 shows the electric field lines around three-point charges A, B and C.
(a) Which charges are positive?
(b) Which charge has the largest magnitude? Why?
(c) In which region or regions of the picture could the electric field be zero? Justify your answer.
(i) near A, (ii) near B, (iii) near C, (iv) nowhere.

Answer:
i) A and C are positive charges as the electric field lines are protruding out of these two charges.ii) Charge C has the largest magnitude as it has the greatest number of electric field lines coming out.
iii) The neutral region is in between the charges A and C. Charges C is a stronger charge; therefore the neutral point naturally lies near to A (charge A is a weak charge).
Question:1.25
Five charges, q each are placed at the corners of a regular pentagon of side 'a' (Fig. 1.12).

(a)
(i) What will be the electric field at O, the center of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
Answer:
i) The net charge at the centre will be zero as all the charges are equidistant from the centre and they will cancel out each other.ii) It can be written as that the electric field at O due to A and all other charges is zero. The equation would be as follows:
$\vec{E}_A+\vec{E}_{f\! our\: charges}=0$
Hence $\vec{E}_{f\! our\: charges}=-\vec{E}_A\: \: or \left | \vec{E}_{f\! our\: charges} \right |= \left |\vec{E}_A \right |$
When charge q is removed from A, net electric field at the centre due to
remaining charges $\left | \vec{E}_{f\! our\: charges} \right |= \left |\vec{E}_A \right |=\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\: \: along\: \: OA$
(iii) If charge q at A is replaced by -q, then electric field due to this negative charge
$\vec{E_{-q}}=\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\: along \: OA$
Hence net electric field at the centre
$\vec{E_{net}}=\vec{E_{-q}}+\vec{E}_{force \: charge}=\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\: +\frac{1}{4\pi \varepsilon _0}\frac{q}{r^{2}}\:$
$\vec{E}_{net}=\frac{1}{4\pi \varepsilon _0}\frac{2q}{r^{2}}\: \: along \: OA$
b) If pentagon is replaced by a polygon and charge Q at each corner, then also they all will cancel out each other, and the net electric field at O will be zero.
NCERT Exemplar Class 12 Physics Solutions Chapter 1 Long Answer
Question:1.26
In 1959, Lyttleton and Bondi suggested that the expansion of the universe could be explained if matter carried a net charge. Suppose that the universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
(a) Find the critical value of y such that expansion may start.
(b) Show that the velocity of expansion is proportional to the distance from the centre.
Answer:
(a) Let us suppose that universe is a perfect sphere of radius $R$ and its constituent hydrogen atoms are distributed uniformly in the sphere.
As hydrogen atom contains one proton and one electron, charge on each hydrogen atom.
$
e_H=e_P+e=-(1+Y) e+e=-Y e=(Y e)
$
If $E$ is electric field intensity at distance $R$, on the surface of the sphere, then according to Gauss' theorem,
$
\begin{aligned}
\oint \text { E.ds } & =\frac{q}{\varepsilon_0} \text { i.e., } E\left(4 \pi R^2\right)=\frac{4}{3} \frac{\pi R^3 N|Y e|}{\varepsilon_0} \\
E & =\frac{1}{3} \frac{N|Y e| R}{\varepsilon_0} --------(i)
\end{aligned}
$
Now, suppose, mass of each hydrogen atom $\simeq m_P=$ Mass of a proton, $G_R=$ gravitational field at distance $R$ on the sphere.
Then
$
\begin{aligned}
-4 \pi R^2 G_R & =4 \pi G m_P\left(\frac{4}{3} \pi R^3\right) N \\
G_R & =\frac{-4}{3} \pi G m_P N R ---------(ii)
\end{aligned}
$
$\therefore$ Gravitational force on this atom is:
$F_G=m_P \times G_R=\frac{-4 \pi}{3} G m_P^2 N R$-----------(iii)
Coulomb force on hydrogen atom at $R$ is:
$F_C=(Y e) E=\frac{1}{3} \frac{N Y^2 e^2 R}{\varepsilon_0}$ ------------[from Eq. (i)]
Now, to start expansion $F_C>F_G$ and critical value of $Y$ to start expansion would be when
$
\begin{array}{rlrl}
\Rightarrow& F_C =F_G \\
\Rightarrow & \frac{1}{3} \frac{N Y^2 e^2 R}{\varepsilon_0} =\frac{4 \pi}{3} G m_P^2 N R \\
\Rightarrow & Y^2 =\left(4 \pi \varepsilon_0\right) G\left(\frac{m_P}{e}\right)^2 \\
\Rightarrow & Y^2 =\frac{1}{9 \times 10^9} \times\left(6.67 \times 10^{-11}\right)\left(\frac{\left(1.66 \times 10^{-27}\right)^2}{\left(1.6 \times 10^{-19}\right)^2}\right)\\
\Rightarrow & Y^2=79.8 \times 10^{-38} \\
\Rightarrow & Y =\sqrt{79.8 \times 10^{-38}}=8.9 \times 10^{-19} \simeq 10^{-18}
\end{array}
$
Thus, $10^{-18}$ is the required critical value of $Y$ corresponding to which expansion of universe would start.
(b) Net force experience by the hydrogen atom is given by
$
F=F_C-F_G=\frac{1}{3} \frac{N Y^2 e^2 R}{\varepsilon_0}-\frac{4 \pi}{3} G m_P^2 N R
$
If acceleration of hydrogen atom is represent by $d^2 R / d t^2$, then
$
\begin{aligned}
& m_p \frac{d^2 R}{d t^2}=F=\frac{1}{3} \frac{N Y^2 e^2 R}{\varepsilon_0}-\frac{4 \pi}{3} G m_p^2 N R \\
& =\left(\frac{1}{3} \frac{N Y^2 e^2}{\varepsilon_0}-\frac{4 \pi}{3} G m_p^2 N\right) R \\
& \therefore \quad \frac{d^2 R}{d t^2}=\frac{1}{m_p}\left[\frac{1}{3} \frac{N Y^2 e^2}{\varepsilon_0}-\frac{4 \pi}{3} G m_p^2 N\right] R=\alpha^2 R \\
& \text { where, } \\
& \alpha^2=\frac{1}{m_p}\left[\frac{1}{3} \frac{N Y^2 e^2}{\varepsilon_0}-\frac{4 \pi}{3} G m_P^2 N\right]
\end{aligned}
$
The general solution of Eq. (iv) is given by $R=A e^{\alpha t}+B e^{-\alpha t}$.
We are looking for expansion, here, so $B=0$ and $R=A e^{\alpha t}$.
$\Rightarrow \quad$ Velocity of expansion, $v=\frac{d R}{d t}=A e^{\alpha t}(\alpha)=\alpha A e^{\alpha t}=\alpha R$
Hence, $v \propto R$ i.e., velocity of expansion is proportional to the distance from the centre.
Question:1.27
Consider a sphere of radius R with charge density distributed as
\begin{aligned}
\rho(r) & =k r \quad \text { for } r \leq R \\
& =0 \quad \text { for } r>R .
\end{aligned}
(a) Find the electric field at all points r.
(b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero? Assume that the introduction of the proton does not alter the negative charge distribution.
Answer:
a) The charge density distribution expression in the sphere tells that the electric field is radial.
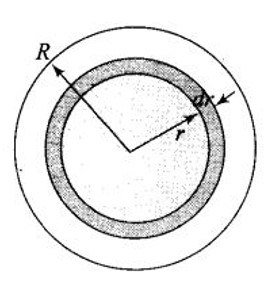
Let us consider a sphere S of radius R and two hypothetic spheres of radius $r< R$ and $r> R$.
Let us first consider for point $r< R$, electric field intensity will be given by,
$\oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}\int \rho \: dV$
Here $dV =4\pi r^2\:dr$
$\Rightarrow \oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}4 \pi K \int_{0}^{r}r^3dr\left ( \because \rho \left ( r \right )=Kr \right )$
$\Rightarrow \left ( E \right )4 \pi r^2= \frac{4 \pi K}{\varepsilon _0}\frac{r^4}{4}$
We get
$E= \frac{1}{4\varepsilon _0}Kr^2$
As charge density is positive, it means the direction of E is radially outwards.
Now consider points $r>R$ , electric field intensity will be given by
$\oint \vec{E}.d\vec{S}= \frac{1}{\varepsilon _0}\int \rho dV$
$\Rightarrow E(4 \pi r^2)= \frac{4 \pi K}{\varepsilon _0}\int_{0}^{R}r^3dr=\frac{4 \pi K}{\varepsilon _0}\frac{R^4}{4}$
Which gives $E=\frac{K}{4 \varepsilon _0}\frac{R^4}{r^2}$
Here also the charge density is again positive. So, the direction of E is radially outward.
(b) The two proton must be placed symmetrically on the opposite sides of the centre along a diameter. This can be shown by
the figure given below. Charge on the sphere,
$\\q=\int_{0}^{R}\rho dV= \int_{0}^{R}\left ( Kr \right )4 \pi r^2dr\\$
$\\ q=4 \pi K\frac{R^4}{4}2e\\ \quad \\$
$\because K=\frac{2e}{\pi R^4}$

The proton 1 and 2 are embedded at distance r from the centre of the sphere as shown, then attractive force on proton 1 due to charge distribution is
$F_1=eE=\frac{-eKr^2}{4\varepsilon _0}$
and repulsive force on proton 1 due to proton 2 is
$F_2=\frac{e^2}{4 \pi\varepsilon _0 (2r)^2}$
Net force on proton 1, $F=F_1+F_2$
$F=\frac{-eKr^2}{4\varepsilon _0}+\frac{e^2}{16 \pi \varepsilon _0r^2}$
Thus, net force on proton 1 will be zero, when
$\frac{er^22e}{4\varepsilon _0 \pi R^4}= \frac{e^2}{16 \pi \varepsilon _0r^2}$
$\Rightarrow r^4= \frac{R^4}{8}$
Hence the protons must be at a distance $r=\frac{R}{(8)^{1/4}}$ from the centre.
Question:1.28
Two fixed, identical conducting plates $(\alpha and \beta )$, each of surface area S are charged to –Q and q, respectively, where $Q > q > 0$. A third identical plate ($\gamma$), free to move is located on the other side of the plate with charge q at a distance d (Fig 1.13). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst $(\beta \: and\: \gamma )$
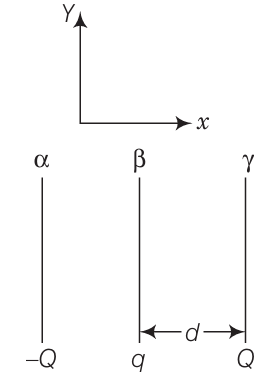
(a) Find the electric field acting on the plate $\gamma$ before the collision.
(b) Find the charges on β and $\gamma$ after the collision.
(c) Find the velocity of the plate $\gamma$ after the collision and at a distance d from the plate β.
Answer:
(a) Net electric field field at plate $\gamma$ before collision is vector sum of electric field at plate $\gamma$due to plate $\alpha\: and\: \beta$.
The electric field at plate $\gamma$ due to plate $\alpha$ is $\vec{E}_1= \frac{Q}{S(2\varepsilon _0)}(-\hat{i}),$
The electric field at plate $\gamma$ due to plate $\beta$ is $\vec{E}_2= \frac{q}{S(2\varepsilon _0)}(\hat{i}),$
Hence the net electric field at plate $\gamma$ before collision is
$\\ \vec{E}=\vec{E}_1+\vec{E}_2= \frac{q-Q}{S(2\varepsilon _0)}(\hat{i}),\\ \\ \vec{E}=\vec{E}_1+\vec{E}_2= \frac{Q-q}{S(2\varepsilon _0)}(\hat{i}),$
Or $\frac{Q-q}{S(2\varepsilon _0)}$ to the left, if $Q>q$
(b) During collision, plates $\alpha\: and\: \beta$ are in contact with each other, hence their potential becomes the same.
Suppose charge on plate $\beta \: is\: q_1\:$ and charge on plate $\gamma \: is\: q_2\:$. at any point O , in between the two plates, the electric field must be zero.
Electric field at O due to $\alpha$,
$\vec{E}_\alpha = \frac{Q}{S(2\varepsilon _0)}\left (- \hat{i} \right )$
Electric field at O due to $\beta$,
$\vec{E}_\beta = \frac{q_1}{S(2\varepsilon _0)}\left ( \hat{i} \right )$
Electric field at O due to $\gamma$,
$\vec{E}_\gamma = \frac{q_2}{S(2\varepsilon _0)}\left (- \hat{i} \right )$
As the electric field at O is zero, therefore
$\frac{Q+q_2}{S(2\varepsilon _0)}=\frac{q_1}{S(2\varepsilon _0)}\\ \\ \because Q+q_2=q_1$
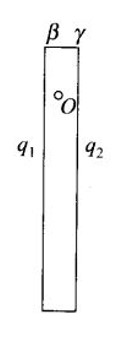
As there is no loss of charge on collision,
$Q+q=q_1+q_2$
On solving Equ. (1) and (2) We get
$q_1=(Q+q/2)=$Charge on plate $\beta$
$q_1=(q/2)=$Charge on plate $\gamma$
(c) Let the velocity be $\nu$ at the distance d from plate $\beta$ after the collision.
If m is the mass of the plate $\gamma$, then the gain in K.E. over the round trip must be equal to the work done by the electric field.
After the collision, electric field at plate $\gamma$ is
$\vec{E}_2= \frac{Q}{2\varepsilon _0S}(-\hat{i}),+\frac{\left ( Q+q/2 \right )}{2\varepsilon _0S}\hat{i}=\frac{\left ( q/2 \right )}{2\varepsilon _0S}\hat{i}$
Just before collision, electric field at plate $\gamma$ is
$\vec{E}_1= \frac{Q-q}{2\varepsilon _0S}\: \hat{i}.$
If F1 is force on plate before collision., then
$F_1=\vec{E}_1Q= \frac{\left ( Q-q \right )Q}{2\varepsilon _0S}\: \hat{i}\: and\: F_2=\vec{E}_2\frac{q}{2}= \frac{\left ( \frac{q}{2} \right )^{2}}{2\varepsilon _0S}\: \hat{i}$
Total work done by the electric field is the round trip movement of plate $\gamma$,
$W=(F_1+F_2)d=\frac{\left [ \left ( Q-q \right )Q+\left ( q/2 \right )^{2} \right ]d}{2\varepsilon _0S}=\frac{\left ( Q-q/2 \right )^{2}d}{2\varepsilon _0S}$
If m is the mass of plate $\gamma$, the KE gained by the plate = $\frac{1}{2}m\nu ^2$
According to work energy principle,
$\frac{1}{2}m\nu ^2=W $
$\Rightarrow \frac{1}{2}m\nu ^2=\frac{\left ( Q-q/2 \right )^{2}d}{2\varepsilon _0S}$
$\Rightarrow \nu =\left ( Q-q/2 \right )\left ( \frac{d}{m\varepsilon _0S} \right )^{1/2}$
Question:29
There is another useful system of units, besides the SI/mks system, called the cgs (centimetre-gram-second) system. In this system, Columb's law is given by
$F=\frac{Qq}{r^2}$
where the distance r is measured in $cm (= 10^{-2} m)$, F in dynes $(=10^{-5} N)$ and the charges in electrostatic units (es units), where 1es unit of charge $\frac{1}{3}\times10^{-9}C$
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by $c = 2.99792458 \times 10^8 \: m/s$. An approximate value of c then is $c = [3] \times 10^8 m/s.$
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge $= x\: C,$ where x is a dimensionless number. Show that this gives
$\frac{1}{4\pi\epsilon_0}=[3]^2\times10^{9}\frac{Nm^2}{C^2}$
Answer:
$(i)$ Acording to relation,
$F =\frac{Qq}{r^2}= 1dyne= \frac{\left [ esu\; of\: charge \right ]^2}{\left [ 1cm \right ]^{2}}$
So, 1 esu of charge $=\left ( 1dyne \right )^{1/2}\times 1 cm$
$F^{1/2}.L=\left [ MLT^{2} \right ]^{1/2}\left [ L \right ]= \left [ M^{1/2}L^{3/2}T^{1} \right ]$
$\Rightarrow$ Hence, [1 esu of charge] =$M^{1/2}L^{3/2}T^{1}$
Thus the charge in C.G.S. unit (in esu) is represented in terms of fractional power 1/2 of M and 3/2 of L.
$(ii)$ If two charge each of magnitude 1 esu separated by 1 cm, Coulomb force on the charge is 1 dyne = $10^{-5}N.$
Let 1 esu of charge =x C, where x is a dimensionless number. We can consider a situation, two charges of magnitude x C separated by $10^{-2}m.$
The force between the charge
$F=\frac{1}{4 \pi \varepsilon _0}\frac{x^{2}}{\left ( 10^{-2} \right )^{2}}= 1dyne=10^{-5}N$
$\therefore \frac{1}{4 \pi \varepsilon _0}= \frac{10^{-9}}{x^{2}}\frac{Nm^{2}}{C^{2}}$
Taking, $\\x=\frac{1}{\left | 3 \right |\times 10 ^{9}},\\$
$We \: get\: \: \frac{1}{4\pi \varepsilon _0}=10^{-9}\times \left | 3 \right |^{2}\times 10^{18} \\ \frac{1}{4\pi \varepsilon _0}=9\times 10^{9}\frac{Nm^{2}}{C^{2}}$
Question:30
Answer:
Let the charge q is displaced slightly by $x(x<<d)$perpendicular to the line joining the two fixed charges. The net force on the charge q will be towards O.The motion of charge -q to be simple harmonic if the force on charge q must be proportional to its distance from the centre O and is directed towards O.The net force on the charge $F_{net}= 2F \cos\theta$
Here $F=\frac{1}{4\pi \varepsilon _0}\frac{q(q)}{r^2}= \frac{1}{4\pi \varepsilon _0}\frac{q^2}{\left ( d^2+x^2 \right )}$
And$\cos \theta =\frac{x}{\sqrt{x^2+d^2}}$
Hence, $F_{net}=2 \left [ \frac{1}{4\pi \varepsilon _0}\frac{q^2}{\left ( d^2+x^2 \right )} \right ]\left [ \frac{x}{\sqrt{x^2+d^2}} \right ]$
$= \frac{1}{2\pi \varepsilon _0}\frac{q^2x}{\left ( d^2+x^2 \right )^{3/2}}=\frac{1}{2\pi \varepsilon _0}\frac{q^2x}{d^3\left ( 1+\frac{x^2}{d^2} \right )^{3/2}}$
As $x<<d, then F_{net}=\frac{1}{2 \pi \varepsilon _0}\frac{q^2x}{d^3}\: or \: F_{net}=Kx$
i.e. force on charge q is proportional to its displacement from the centre O and it is directed towards O.
Hence, the motion of charge q would be simple harmonic, where
$\omega = \sqrt{\frac{K}{m}}\\ and \: T=\frac{2 \pi }{\omega}=2 \pi\sqrt{\frac{m}{K}}$
$\Rightarrow T= 2 \pi \sqrt{\frac{m.4 \pi \varepsilon _0d^3}{2q^2}}=\left [ \frac{8 \pi^3 \varepsilon _0md^3}{q^2} \right ]^{1/2}$
Question:31
Total charge –Q is uniformly spread along the length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.
(a) Show that the particle executes a simple harmonic oscillation.
(b) Obtain its time period.
Answer:
Let the charge q is displaced slightly by $z\left ( z< < R \right )$ along the axis of ring. Let force on the charge q will be towards O. The motion of charge q will be simple harmonic, it the force on charge q must be proportion to z and is directed towards O.
Electric field at axis of the ring at a distance z from the centre of ring
$E=\frac{1}{4\pi \varepsilon _0}\frac{Q_z}{\left ( R^2+Z^2 \right )^{3/2}};$towords O
the net force on the charge $F_{net}=qE$
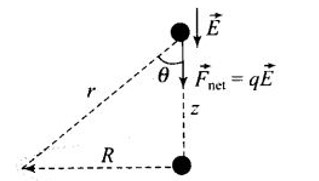
$F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{\left ( R^2+Z^2 \right )^{3/2}};$
$\Rightarrow$ $F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{R^3\left ( \frac{1+z^2}{R^2} \right )^{3/2}}$
As $z<<R\: then,$
$\Rightarrow$ $F_{net}=\frac{1}{4\pi \varepsilon _0}\frac{qQz}{R^3\left ( \frac{1+z^2}{R^2} \right )^{3/2}}$ or $\vec{F}_{net}=-K\vec{z}$
Where $K=\frac{Qq}{4\pi \varepsilon _{0}R^{3}}=constant$
Clearly, the force on q is proportional to the negative of its displacement. Therefore the motion of q is simple harmonic.
$\begin{aligned} & \omega \sqrt{\frac{K}{m}} \text { and } T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m}{K}} \\ & T=2 \pi \sqrt{\frac{m 4 \pi \varepsilon_0 R^3}{Q q}} \\ & T=2 \pi \sqrt{\frac{4 \pi \varepsilon_0 m R^3}{Q q}}\end{aligned}$
NCERT Exemplar Class 12 Physics Chapter Wise Links
NCERT Exemplar Class 12 Solutions
Also, check the NCERT solutions of questions given in the book
Also, read NCERT Solution subject wise
- NCERT Solution for Class 12 Physics
- NCERT Solution for Class 12 Chemistry
- NCERT Solution for Class 12 Maths
- NCERT Solution for Class 12 Biology
Must read NCERT Notes subject-wise
- NCERT Notes for Class 12 Physics
- NCERT Notes for Class 12 Chemistry
- NCERT Notes for Class 12 Maths
- NCERT Notes for Class 12 Biology
Also, check the NCERT Books and NCERT Syllabus here:
Frequently Asked Questions (FAQs)
Exemplar questions will be more practical and will be framed to test your understanding clarity as opposed to textbook questions which will be easy to understand.
Absolutely. Exemplar questions are correlated in a manner that enhances your knowledge since they engage critical thinking, analytical reasoning, and application of theories in the real life.
The exemplar answers enable the student to grasp the difficult topics dealing with electric charge, electric field, and Coulomb law, using a tremendous variety of problems, reinforcing conceptual and problem-solving abilities at both the board and competitive examination levels.
These solutions are MCQs, short answer questions, long answer questions, and very long answer questions, aimed at diffident levels of knowledge.
Yes, every question is answered in a step-by-step detail in order that students get a clear sense of how and why the answer(s) were obtained.
Questions related to CBSE Class 12th
On Question asked by student community
Hello
You will be able to download the CBSE Previous Year Board Question Papers from our official website, careers360, by using the link given below.
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers
I hope this information helps you.
Thank you.
Hello
You will be able to download the CBSE Pre-Board Class 12 Question Paper 2025-26 from our official website by using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-pre-board-class-12-question-paper-2025-26
I hope this information helps you.
Thank you.
Hello,
Yes, it's completely fine to skip this year's 12th board exams and give them next year as a reporter or private candidate, allowing you to prepare better; the process involves contacting your current school or board to register as a private candidate or for improvement exams during the specified
HELLO,
Yes i am giving you the link below through which you will be able to download the Class 12th Maths Book PDF
Here is the link :- https://school.careers360.com/ncert/ncert-book-for-class-12-maths
Hope this will help you!
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters