NCERT Class 11 Chemistry Chapter 6 Notes Thermodynamics - Download PDF

Thermodynamics is an important branch of chemistry that deals with the change in energy in any Physical and Chemical process. It examines how energy moves between different systems and their surroundings, with an emphasis on important ideas like work and heat, along with the basic rules that control these changes. Thermodynamics explains the reason for the occurrence of any reaction, transfer of energy, etc. It helps us understand how chemical processes function, how materials change states, and how reactions balance. It also allows us to determine whether a reaction can occur on its own by calculating the amount of energy required.

Thermodynamics is something we deal with every day. Consider how automobile engines convert fuel into action or how refrigerators keep food fresh. These concepts are vital for using energy effectively. Our bodies use the same ideas- metabolism turns chemical energy from food into the energy needed to live. NCERT Notes of class 11 are according to Class 11 CBSE Chemistry Syllabus, giving students valuable knowledge about how energy changes and how to use that understanding in real-world situations. For other chapters, the NCERT notes are designed by experts for an excellent overview of the subject for the pre

Also, students can refer,

NCERT Notes for Class 11 Chemistry Chapter 5 Download PDF

These concise NCERT notes cover all the key concept of chapter 5 to help students in quick revision before exam. You can download NCERT notes pdf from the button given below:

Download PDF

NCERT Notes for Class 12 Chapter 5 Thermodynamics

The NCERT Notes of thermodynamics contain a concise overview of the chapter, including all the important topics and formulas. It can be used for a quick revision during exam time. It includes types of systems, work, and calculation of internal energy and enthalpy. Each topic is discussed in detail below.

System and Surroundings

A system can be defined as where the observations were made, it is the part of the universe.

Surrounding can be defined as the part other than the system is, surrounding.

The system and surroundings can be differentiated by a wall called a boundary.

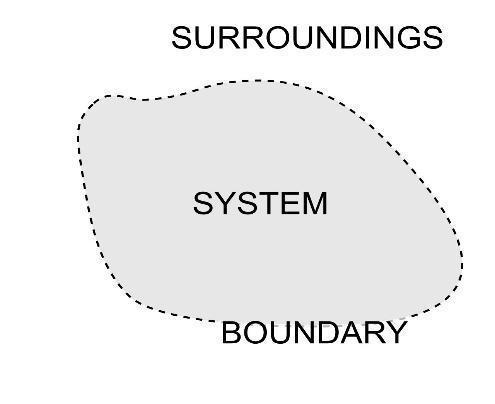
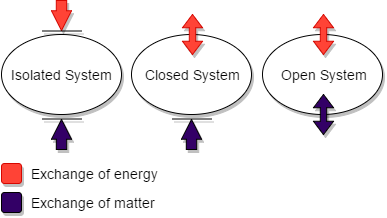
Types of the system:

The system can be further divided into three categories such as-

1. Open system- Boundary is imaginary in this system and exchange of mass or matter and energy both can be possible between system and surroundings. Example: Open beaker.

2. Closed system- No exchange of matter occurs, but the exchange of energy is possible between the system and its surroundings. Example: closed container of steel or copper.

3. Isolated system- No exchange of matter or energy can be possible. Example: Closed container like a thermos flask.

The State of the System

In general concern when we have to make any calculations we require measurable quantities or properties.

Those quantities are temperature, pressure, and the volume combined to form the composition of the system. But in order to deal with these quantities, we must have average conclusions of such measurements so we introduce a term called state functions or state variables. These quantities like pressure(p), volume(V), temperature(T), and amount(n).such variables like p, V, T, n are stated as state variables or state functions.

Internal Energy as a State Function:

The combined energy or sum of energies, such as mechanical, electrical or chemical are so-called internal energy of the system. This can be denoted in thermodynamics by the letter ‘U’. This can be affected by a change in any of the following:

• Heat goes into and out of the system

• Work can be done on the system or by the system.

• Matter; Exchange of matter( entering or leaving)

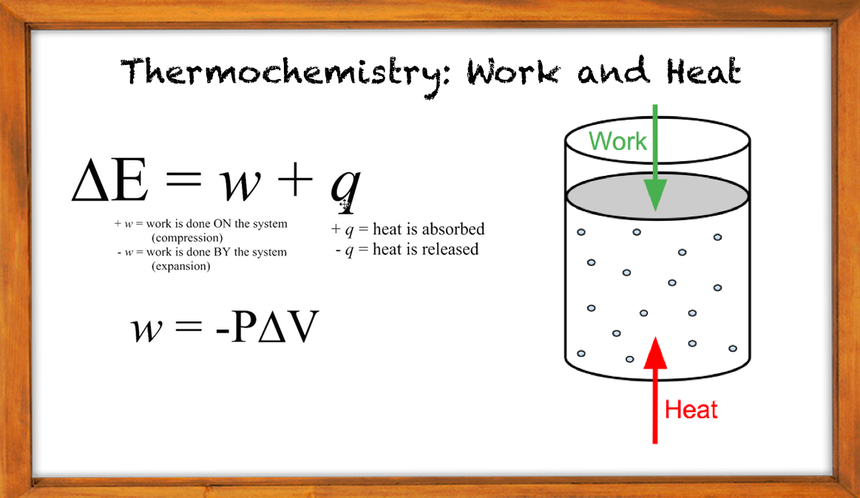
General case: This can be shown using an equation.

∆U=q+w

Here the change in internal energy is the sum of heat passing in and out and the work done. It is independent of the change and also depends on the initial and final state of the system. The equation that we get for change in internal energy is the mathematical form of the First law of thermodynamics.

Adiabatic system: It is the system in which the system and surroundings are separated by a wall, where no transfer or exchange of matter or energy occurs.

Applications

Work: Here we take an example of a cylinder or piston, which is fitted perfectly and is filled with a frictionless container with one mole of gas.

Let us first discuss the variables to calculate the work done.

The pressure of the gas=p

The volume of the gas=V

The external pressure of the gas=pext

Area of cross section=A

The piston is moved to a certain distance, taken as length=l

Change in volume$\mathrm{\Delta }\mathrm{V}=\mathrm{A}\times \mathrm{I}=({\mathrm{V}}_{\mathrm{f}}-{\mathrm{V}}_{\mathrm{I}})$

So here, the pressure inside the piston becomes

p=FA

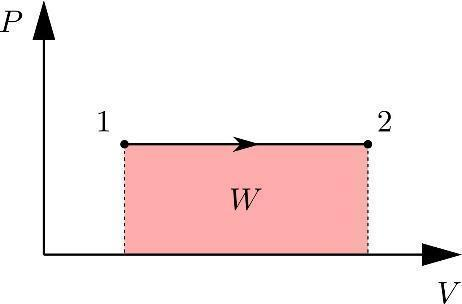
Case1: Expansion process

In the case of this process, work is done by the system, by expanding the volume of the system. When the work is done by the system then the negative sign convention will be used in it. so the value of work done will be

W=-p∆V

Now consider the two cases of expansion of ideal gas.

1. Work is to be done in isothermal and reversible condition, where the expansion of ideal gas occur.

Reversible work is taken from the initial volume to the final volume.

${\mathrm{w}}_{\text{rev }}=-{\int }_{V_i}^{V_f}{p}_{\text{ex }}dV=-{\int }_{V_i}^{V_f}(p_{\text{in }}\pm dp)dV$

Since $dp\times dV$ is very small, we can write

${\mathrm{w}}_{rev}=-{\int }_{V_i}^{V_f}{p}_{in}dV$

Now, the pressure of the gas ( $p_{\text{in }}$, which we can write as $p$ now) can be expressed in terms of its volume through the gas equation. For $n$ mol of an ideal gas i.e., $pV=nRT$

$\Rightarrow p=\frac{n\mathrm{R}T}{V}$

Therefore, at constant temperature (isothermal process),

$\begin{array}{rl}& {\mathrm{w}}_{\mathrm{rev}}=-{\int }_{V_i}^{V_f}n\mathrm{R}T\frac{dV}{V}=-n\mathrm{R}T\ln \frac{V_f}{V_i}\\ & =-2.303n\mathrm{R}T\log \frac{V_f}{V_i}\end{array}$

B. Isothermal condition, where the expansion of an ideal gas occurs.

• For irreversible change:

$q=-\mathrm{w}=p_{ex}(V_f-V_i)$

• For reversible change

$\begin{array}{rl}& q=-\mathrm{w}=n\mathrm{R}T\ln \frac{V_f}{V_i}\\ & =2.303n\mathrm{R}T\log \frac{V_f}{V_i}\end{array}$

• For adiabatic change, q=0,

$\mathrm{\Delta }U={\mathrm{w}}_{\mathrm{ad}}$

Enthalpy

Enthalpy can be denoted by the letter ‘H’.

Enthalpy is defined as the sum of pressure-volume and internal energy.

Change in enthalpy can be defined as the heat being evolved or absorbed at constant pressure conditions in a given system.

For finite changes at constant pressure, we can write the equation as,

$\mathrm{\Delta }H=\mathrm{\Delta }U+\mathrm{\Delta }pV$
Since $p$ is constant, we can write

$\mathrm{\Delta }H=\mathrm{\Delta }U+p\mathrm{\Delta }V$

For the Exothermic process, Heat is given out of the system, whereas for the Endothermic process, heat is given to the system from the surroundings.

Relationship between Change in enthalpy and change in internal energy of the system

$\mathrm{p}\mathrm{\Delta }\mathrm{V}=\mathrm{\Delta }{\mathrm{n}}_{\mathrm{g}}\mathrm{RT}$

$\mathrm{\Delta }\mathrm{H}=\mathrm{\Delta }\mathrm{U}+\mathrm{\Delta }{\mathrm{n}}_{\mathrm{g}}\mathrm{RT}$

1. Extensive property:

Extensive property can be defined as that property in which the value depends on the quantity or the size that is present in the system.

Examples of extensive properties are mass, enthalpy, volume, etc.

2. Intensive property:

Intensive property can be defined as that property in which the value does not depend on the quantity or the size that is present in the system.

Examples of intensive properties are temperature, density, etc.

3. Heat capacity:

Heat capacity may be defined increase in temperature that is directly proportional to heat transferred.

The increase in temperature is proportional to the heat transferred

$q=\text{ coeff }\times \mathrm{\Delta }T$
The magnitude of the coefficient depends on the size, composition and nature of the system. We can also write it as $q=C\mathrm{\Delta }T$.

To find out the heat, q, required to raise the temperature of a sample, we multiply the specific heat of the substance, c, by the mass m, and temperature change, ∆T, as

$q=c\times m\times \mathrm{\Delta }T=C\mathrm{\Delta }T$

4. Relationship between the value of C_p and C_v.

Constant volume value of heat capacity; C_v.

Constant pressure value of heat capacity; C_p.

We can write an equation for heat, $q$
at constant volume as $q_V=C_V\mathrm{\Delta }T=\mathrm{\Delta }U$
at constant pressure as $q_p=C_p\mathrm{\Delta }T=\mathrm{\Delta }H$
The difference between $C_p$ and $C_V$ can be derived for an ideal gas as:

For a mole of an ideal gas

$\begin{array}{rl}& \mathrm{\Delta }H=\mathrm{\Delta }U+\mathrm{\Delta }(pV)\\ & =\mathrm{\Delta }U+\mathrm{\Delta }(\mathrm{R}T)\\ & =\mathrm{\Delta }U+\mathrm{R}\mathrm{\Delta }T\\ & \therefore \mathrm{\Delta }H=\mathrm{\Delta }U+\mathrm{R}\mathrm{\Delta }T\end{array}$
On putting the values of $\mathrm{\Delta }H$ and $\mathrm{\Delta }U$, we have

$\begin{array}{rl}& C_p\mathrm{\Delta }T=C_V\mathrm{\Delta }T+\mathrm{R}\mathrm{\Delta }T\\ & C_p=C_V+\mathrm{R}\end{array}$

$C_p-C_v=R$

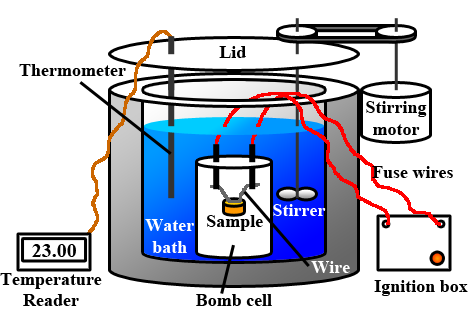
Measurement of ∆U and ∆H: Calorimetry

Measurement of the value of change in internal energy and change in enthalpy with Bomb calorimeter.

Enthalpy changes occur during the process of phase transformation.

• Enthalpy of Fusion: Enthalpy of fusion can be defined as the conversion of one mole of a solid is accompanied to change it in liquid. The condition of fusion is governed at its melting point

• Enthalpy of Vaporisation: Enthalpy of vaporization can be defined as the conversion of one mole of a solid accompanied to change it in liquid, the condition of fusion is governed by its boiling point.

• Enthalpy of Sublimation: Enthalpy of sublimation is defined as the change in when one mole of a solid is converted to a gaseous state at its melting point. But the temperature is below its melting range.

• Enthalpy of Combustion: Enthalpy of fusion is defined as the change in when one mole of substance burns in excess amount of air.

• Standard enthalpy of formation: It is defined as inthe standard condition of temperature at 273K and pressure at 1 atm formation of one mole of substance occurs with the help of their constituent elements.

• Thermochemical equations: It is defined as in chemical reaction when the products and reactants are present with their physical value and value of∆rH present such reaction equation is known asa Thermochemical equation.

Enthalpy change, ∆_rH of a Reaction – Reaction Enthalpy

In a chemical reaction, reactants are converted into products and is represented by,

Reactants $\to$ Products
The enthalpy change accompanying a reaction is called the reaction enthalpy. The enthalpy change of a chemical reaction, is given by the symbol ${\mathrm{\Delta }}_{r}H$
${\mathrm{\Delta }}_{r}H=$ (sum of enthalpies of products) - (sum of enthalpies of reactants)

$=\sum _i{\mathrm{a}}_i{H}_{\text{products }}-\sum _i{b}_i{H}_{\text{reactants }}$
Here symbol $\sum$ (sigma) is used for summation and ${\mathrm{a}}_i$ and ${\mathrm{b}}_i$ are the stoichiometric coefficients of the products and reactants respectively in the balanced chemical equation. For example, for the reaction

$\begin{array}{rl}& {\mathrm{CH}}_4(\mathrm{g})+2{\mathrm{O}}_2(\mathrm{g})\to {\mathrm{CO}}_2(\mathrm{g})+2{\mathrm{H}}_2\mathrm{O}(l)\\ & \begin{array}{rl}{\mathrm{\Delta }}_{r}H& =\sum a_i{H}_{\text{Products }}-\sum b_i{H}_{\text{reactants }}\\ =[H_{\mathrm{m}}^i({\mathrm{CO}}_2,\mathrm{g})+2H_{\mathrm{m}}^i({\mathrm{H}}_2\mathrm{O},t)]& -[H_{\mathrm{m}}({\mathrm{CH}}_4,\mathrm{g})\\ & +2H_{\mathrm{m}}({\mathrm{O}}_2,\mathrm{g})]\end{array}\end{array}$

where $H_{\mathrm{m}}$ is the molar enthalpy.

Standard Enthalpy of Reactions

The standard enthalpy of reaction is the enthalpy change for a reaction when all the participating substances are in their standard states. The standard state of a substance at a specified temperature is its pure form at 1 bar. Standard conditions are denoted by adding the superscript $\ominus$ to the symbol $\mathrm{\Delta }H$, e.g., $\mathrm{\Delta }{H}^{\ominus }$.

Enthalpy Changes During Phase Transformations

Phase transformations also involve energy changes. Ice, for example, requires heat for melting. Normally, this melting takes place at constant pressure (atmospheric pressure), and during phase change, temperature remains constant (at 273 K ).

${\mathrm{H}}_2\mathrm{O}(\mathrm{s})\to {\mathrm{H}}_2\mathrm{O}(t);{\mathrm{\Delta }}_{fus}{H}^{\ominus }=6.00\mathrm{kJ}{\mathrm{mol}}^{-1}$
Here ${\mathrm{\Delta }}_{\text{fus }}{H}^{\ominus }$ is the enthalpy of fusion in standard state. If water freezes, then the process is reversed and an equal amount of heat is given off to the surroundings.

The enthalpies of different processes are-

• The enthalpy change that accompanies the melting of one mole of a solid substance in standard state is called the standard enthalpy of fusion or molar enthalpy of fusion, ${\mathrm{\Delta }}_{fus}{\mathit{H}}^{\ominus }$.
• The amount of heat required to vaporise one mole of a liquid at constant temperature and under standard pressure (1bar) is called its standard enthalpy of vaporisation or molar enthalpy of vaporisation, ${\mathrm{\Delta }}_{vap}{H}^{\ominus }$.
• Standard enthalpy of sublimation, ${\mathrm{\Delta }}_{\text{sub }}{H}^{\ominus }$ is the change in enthalpy when one mole of a solid substance sublimes at a constant temperature and under standard pressure (1bar).

Standard Enthalpy of Formation: The standard enthalpy change for the formation of one mole of a compound from its elements in their most stable states of aggregation (also known as reference
states) is called Standard Molar Enthalpy of Formation. Its symbol is ${\mathrm{\Delta }}_f{\mathit{H}}^{\ominus }$, where the subscript ‘ f ’ indicates that one mole of the compound in question has been formed in its standard state from its elements in their most
stable states of aggregation.

Some reactions with standard molar enthalpies of formation are as follows.

$\begin{array}{rl}& {\mathrm{H}}_2(\mathrm{g})+1/2{\mathrm{O}}_2(\mathrm{g})\to {\mathrm{H}}_2\mathrm{O}(1);\\ & {\mathrm{\Delta }}_f{H}^{\ominus }=-285.8\mathrm{kJ}{\mathrm{mol}}^{-1}\\ & \mathrm{C}(\text{ graphite, }\mathrm{s})+2{\mathrm{H}}_2(\mathrm{g})\to {\mathrm{Ch}}_4(\mathrm{g});\\ & {\mathrm{\Delta }}_f{H}^{\ominus }=-74.81\mathrm{kJ}{\mathrm{mol}}^{-1}\\ & 2\mathrm{C}(\text{ graphite, }\mathrm{s})+3{\mathrm{H}}_2(\mathrm{g})+1/2{\mathrm{O}}_2(\mathrm{g})\to {\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}(1);\\ & {\mathrm{\Delta }}_f{H}^{\ominus }=-277.7\mathrm{kJ}{\mathrm{mol}}^{-1}\end{array}$

The following general equation can be used for the enthalpy change calculation.

${\mathrm{\Delta }}_r{H}^{\ominus }=\sum _i{\mathrm{a}}_i{\mathrm{\Delta }}_f{H}^{\ominus }$ (products) $-\sum _i{\mathrm{b}}_i{\mathrm{\Delta }}_f{H}^{\ominus }$ (reactants)

where a and b represent the coefficients of the products and reactants in the balanced equation.

Thermochemical Equations:

It would be necessary to remember the following conventions regarding thermochemical equations.
1. The coefficients in a balanced thermochemical equation refer to the number of moles (never molecules) of reactants and products involved in the reaction.
2. The numerical value of $Delt{a}_r{H}^{\ominus }$ refers to the number of moles of substances specified by an equation. Standard enthalpy change ${\mathrm{\Delta }}_r{H}^{\ominus }$ will have units as $\mathrm{kJ}{\mathrm{mol}}^{-1}$.

3. When a chemical equation is reversed, the value of $Delt{a}_r{H}^{\ominus }$ is reversed in sign.

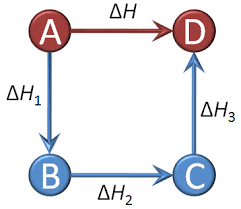
Hess’s Law

It is defined as Hess’s law for constant heat summation.

In general, to solve the questions we can write the equation as follows:

• On combining the two reactions we get the final result as shown above.

• The constant heat summation law suggests that whether the heat is absorbed or evolved in one or many steps, the total amount of heat is the same.

Enthalpies for Different Types of Reactions

1. Standard Enthalpy of Combustion (symbol: ${\mathrm{\Delta }}_c{\mathbf{H}}^{\ominus }$ ): Standard enthalpy of combustion is defined as the enthalpy change per mole (or per unit amount) of a substance, when it undergoes combustion and all the reactants and products being in their standard states at the specified temperature. The thermochemical reaction for the combustion of one mole of butane can be given as: $\begin{array}{r}{\mathrm{C}}_4{\mathrm{H}}_{10}(\mathrm{g})+\frac{13}{2}{\mathrm{O}}_2(\mathrm{g})\to 4{\mathrm{CO}}_2(\mathrm{g})+5{\mathrm{H}}_2\mathrm{O}(1)\\ {\mathrm{\Delta }}_C{H}^{\ominus }=-2658.0\mathrm{kJ}{\mathrm{mol}}^{-1}\end{array}$
2. Enthalpy of Atomization (symbol: ${\mathrm{\Delta }}_a{H}^{\ominus }$ ): It is the enthalpy change on breaking one mole of bonds completely to obtain atoms in the gas phase.
3. Bond Enthalpy (symbol: ${\mathrm{\Delta }}_{\text{bond }}{\mathbf{H}}^{\ominus }$ ): Bond enthalpy refers to the energy involved in breaking or forming chemical bonds. It helps estimate the enthalpy change of a reaction based on the bonds broken and formed. It is the enthalpy change when one mole of a specific bond in a gaseous molecule is broken into atoms.
   For example:
   ${\mathrm{H}}_2(\mathrm{g})\to 2\mathrm{H}(\mathrm{g});\mathrm{\Delta }{\mathrm{H}}^{\circ }=435\mathrm{kJ}/\mathrm{mol}$
   ${\mathrm{Cl}}_2(\mathrm{g})\to 2\mathrm{Cl}(\mathrm{g});\mathrm{\Delta }{\mathrm{H}}^{\circ }=242\mathrm{kJ}/\mathrm{mol}$

   In polyatomic molecules like ${\mathrm{CH}}_4$, individual bond energies vary with each successive bond breaking. So, an average (mean bond enthalpy) is used:

   ${\mathrm{CH}}_4(\mathrm{g})\to \mathrm{C}(\mathrm{g})+4\mathrm{H}(\mathrm{g});\mathrm{\Delta }{\mathrm{aH}}^{\circ }=1665\mathrm{kJ}/\mathrm{mol}$

   Mean C-H bond enthalpy $=1/4\times 1665=416\mathrm{kJ}/\mathrm{mol}$
   Though it may slightly vary across compounds, this average is widely used in thermochemical calculations. Bond enthalpy helps estimate the standard enthalpy of a reaction in the gas phase:

   $\mathrm{\Delta }\mathbf{r}{\mathbf{H}}^{\circ }=\mathbf{\Sigma }(\text{ bond enthalpies of bonds broken })-\mathbf{\Sigma }(\text{ bond enthalpies of bonds formed })$

4. Lattice Enthalpy: The lattice enthalpy of an ionic compound is the enthalpy change which occurs when one mole of an ionic compound dissociates into its ions in gaseous state. We use BOrn-Haber Cycle for this enthalpy.

Born-Haber Cycle

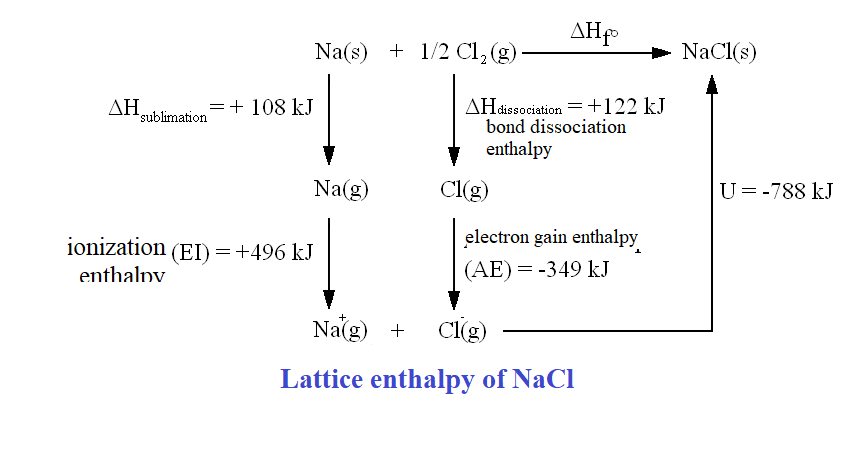
To calculate the lattice enthalpy of NaCl , we apply Hess's Law using the following steps:
Stepwise Enthalpy Changes:
1. Sublimation of $\mathrm{Na}(\mathrm{s})$

$\mathrm{Na}(\mathrm{s})\to \mathrm{Na}(\mathrm{g});\mathrm{\Delta }{\mathrm{subH}}^{\circ }=+108.4\mathrm{kJ}/\mathrm{mol}$

2. Ionization of $\mathrm{Na}(\mathrm{g})$

$\mathrm{Na}(\mathrm{g})\to {\mathrm{Na}}^{+}(\mathrm{g})+{\mathrm{e}}^{-};\mathrm{\Delta }{\mathrm{iH}}^{\circ }=+496\mathrm{kJ}/\mathrm{mol}$

3. Dissociation of ${\mathrm{Cl}}_2(\mathrm{g})$

$1/2{\mathrm{Cl}}_2(\mathrm{g})\to \mathrm{Cl}(\mathrm{g});1/2\mathrm{\Delta }\text{ bondH }{}^{\circ }=+121\mathrm{kJ}/\mathrm{mol}$

4. Electron Gain by Cl(g)

$\mathrm{Cl}(\mathrm{g})+{\mathrm{e}}^{-}\to {\mathrm{Cl}}^{-}(\mathrm{g});\mathrm{\Delta }{\mathrm{egH}}^{\circ }=-348.6\mathrm{kJ}/\mathrm{mol}$

5. Formation of $\mathrm{NaCl}(\mathrm{s})$

${\mathrm{Na}}^{+}(\mathrm{g})+{\mathrm{Cl}}^{-}(\mathrm{g})\to \mathrm{NaCl}(\mathrm{s});\mathrm{\Delta }{\mathrm{fH}}^{\circ }=-411.2\mathrm{kJ}/\mathrm{mol}$
Applying Hess's Law:

$\begin{array}{c}{\mathrm{\Delta }}_{\text{lattice }}{H}^{\circ }={\mathrm{\Delta }}_{\mathrm{f}}{H}^{\circ }+{\mathrm{\Delta }}_{\text{sub }}{H}^{\circ }+{\mathrm{\Delta }}_{\text{bond }}{H}^{\circ }+{\mathrm{\Delta }}_{\mathrm{i}}{H}^{\circ }-{\mathrm{\Delta }}_{\mathrm{eg}}{H}^{\circ }\\ {\mathrm{\Delta }}_{\text{lattice }}{H}^{\circ }=-411.2+108.4+121+496-(-348.6)\\ {\mathrm{\Delta }}_{\text{lattice }}{H}^{\circ }=+788\mathrm{kJ}/\mathrm{mol}\end{array}$
This value corresponds to the process:

$\mathrm{NaCl}(\mathrm{s})\to {\mathrm{Na}}^{+}(\mathrm{g})+{\mathrm{Cl}}^{-}(\mathrm{g})$

The internal energy is slightly less (+783 kJ/mol) due to Δng = 2 (2RT correction).

Using:

${\mathrm{\Delta }}_{\text{sol }}{H}^{\circ }={\mathrm{\Delta }}_{\text{lattice }}{H}^{\circ }+{\mathrm{\Delta }}_{\text{hyd }}{H}^{\circ }$
Given:
Lattice enthalpy = +788 kJ/mol
Hydration enthalpy $=-\mathbf{7}\mathbf{8}\mathbf{4}\mathbf{k}\mathbf{J}/\mathbf{m}\mathbf{o}\mathbf{l}$

${\mathrm{\Delta }}_{\mathrm{sol}}{H}^{\circ }=+788-784=+4\mathrm{kJ}/\mathrm{mol}$

Thus, NaCl dissolves with very little heat change.

5. Enthalpy of Solution (symbol: ${\mathrm{\Delta }}_{\text{sol }}{H}^{\oplus }$ ): Enthalpy of solution of a substance is the enthalpy change when one mole of it dissolves in a specified amount of solvent.

The enthalpy of solution of $\mathrm{AB}(\mathrm{s}),{\mathrm{\Delta }}_{\text{sol }}{H}^{\ominus }$, in water is, therefore, determined by the selective values of the lattice enthalpy, ${\mathrm{\Delta }}_{\text{lattice }}{H}^{\ominus }$ and enthalpy of hydration of ions, ${\mathrm{\Delta }}_{\text{hyd }}{H}^{\ominus }$ as

${\mathrm{\Delta }}_{\text{sol }}{H}^{\ominus }={\mathrm{\Delta }}_{\text{lattice }}{H}^{\ominus }+{\mathrm{\Delta }}_{\text{hyd }}{H}^{\ominus }$

6. Enthalpy of Dilution: The enthalpy of dilution is the heat change that occurs when a solution is diluted, i.e., when more solvent (usually water) is added to a solution. It is usually expressed per mole of solute.

Spontaneity

Spontaneous process: It is the process that has been taken by itself or tends to occur on its own.

The process is not instantaneous in nature. Speed can vary from slow to fast.

Examples of such processes: Common salt dissolves in water on its own.

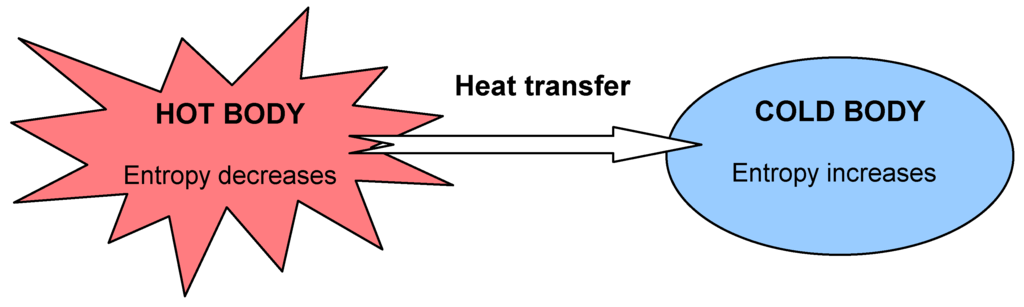
Entropy

Entropy is defined as the degree of disorders and randomness in a system.

The entropy of the gaseous system is found to be more than in the solid state.

Change in entropy∆S=q_revT=∆HT;

Change is entropy can be denoted as ∆S, and is zero for equilibrium condition.

Gibb’s Energy and Spontaneity

It is defined as mathematically ∆G=∆H-T∆S

The above reaction is at constant temperature and pressure.

1. If the value of ∆G is negative or less than zero, the process would be spontaneous.

2. If the value of ∆G is positive or more than zero, the process would be non-spontaneous.

Condition of equilibrium, when all reactants and products are in standard condition, value of ∆G will be:

$0={\mathrm{\Delta }}_{\mathrm{r}}\mathrm{G}-\mathrm{RT}$ InK

$\mathrm{\Delta }\mathrm{rG}={\mathrm{\Delta }}_{\mathrm{r}}\mathrm{H}-\mathrm{T}{\mathrm{\Delta }}_{\mathrm{r}}\mathrm{S}$

=-RTInK

Entropy and Second Law of Thermodynamics

We know that for an isolated system, the change in energy remains constant. Therefore, an increase in entropy in such systems is the natural direction of a spontaneous change. This, in fact is the second law of thermodynamics. Like first law of thermodynamics, second law can also be stated in several ways. The second law of thermodynamics explains why spontaneous exothermic reactions are so common. In exothermic reactions heat released by the reaction increases the disorder of the surroundings and overall entropy change is positive which makes the reaction spontaneous.

Absolute Entropy and the Third Law of Thermodynamics

The entropy of any pure crystalline substance approaches zero as the temperature approaches absolute zero. This is called third law of thermodynamics. This is so because there is perfect order in a crystal at absolute zero. The statement is confined to pure crystalline solids because theoretical arguments and practical evidence have shown that the entropy of solutions and supercooled liquids is not zero at 0 K.

Gibbs Energy Change and Equilibrium

Gibbs energy for a reaction in which all reactants and products are in standard state, ${\mathrm{\Delta }}_r{G}^{\ominus }$ is related to the equilibrium constant of the reaction as follows:

$\begin{array}{rl}0& ={\mathrm{\Delta }}_r{G}^{\ominus }+\mathrm{R}T\ln K\\ \text{ or }{\mathrm{\Delta }}_r{G}^{\ominus }& =-\mathrm{R}T\ln K\\ \text{ or }{\mathrm{\Delta }}_r{G}^{\ominus }& =-2.303\mathrm{R}T\log K\end{array}$
We also know that

${\mathrm{\Delta }}_r{G}^{\ominus }={\mathrm{\Delta }}_r{H}^{\ominus }-T{\mathrm{\Delta }}_r{S}^{\ominus }=-\mathrm{R}T\ln K$

Using the above equation,

1. It is possible to obtain an estimate of $Delta{G}^{\ominus }$ from the measurement of $Delta{H}^{\ominus }$ and $Delta{S}^{\ominus }$, and then calculate $K$ at any temperature for economic yields of the products.
2. If K is measured directly in the laboratory, the value of $Delta{G}^{\ominus }$ at any other temperature can be calculated.

Effect of Temperature on Spontaneity of Reactions is given in the table below-

Thermodynamics Previous Years Questions and Answers

Question: The hydration energies of ${\mathrm{K}}^{+}$and ${\mathrm{Cl}}^{-}$are -x and -y $\mathrm{kJ}/\mathrm{mol}$ respectively. If lattice energy of KCl is -z $\mathrm{kJ}/\mathrm{mol}$, then the heat of solution of KCl is :

(1) $+x-y-z$

(2) $x+y+z$

(3) $z-(x+y)$

(4) $-z-(x+y)$

Answer: $\begin{array}{rl}& \mathrm{\Delta }{\mathrm{H}}_{\text{solution }}=(-\mathrm{\Delta }{\mathrm{H}}_{\text{L.E. }})+\mathrm{\Delta }{\mathrm{H}}_{\text{hydration }}\\ & =-(-z)+(-\mathrm{x}-\mathrm{y})\\ & =\mathrm{z}-(\mathrm{x}+\mathrm{y})\end{array}$

Hence, the correct answer is option (3).

Question: Total enthalpy change for freezing of 1 mol of water at ${10}^{\circ }\mathrm{C}$ to ice at $-{10}^{\circ }\mathrm{C}$ is $$
(Given : ${\mathrm{\Delta }}_{\mathrm{fus}}\mathrm{H}=\mathrm{x}\mathrm{kJ}/\mathrm{mol}$

$\begin{array}{rl}& {\mathrm{C}}_{\mathrm{p}}[{\mathrm{H}}_2\mathrm{O}(\mathrm{l})]=\mathrm{y}\mathrm{J}{\mathrm{mol}}^{-1}{\mathrm{K}}^{-1}\\ & {\mathrm{C}}_{\mathrm{p}}[{\mathrm{H}}_2\mathrm{O}(\mathrm{s})]=\mathrm{z}\mathrm{J}{\mathrm{mol}}^{-1}{\mathrm{K}}^{-1}\end{array}$

(1) $-x-10y-10z$

(2) $-10(100x+y+z)$

(3) $10(100x+y+z)$

(4) $x-10y-10z$

Answer:

$\mathrm{\Delta }H=1\times y(0-10)-x\times 1000+1\times z(-{10}^{\circ }-0^{\circ })$

$\mathrm{\Delta }H=-(10y+10z-1000x)\mathrm{J}$

$\mathrm{\Delta }H=-10(100x+y+z)$ Joule.

Hence, the correct answer is option (2).

Question: The enthalpies of elements in their standard states are taken as zero. The enthalpy of the formation of a compound

1. is always negative
2. is always positive
3. maybe positive or negative
4. is never negative

Answer: It can be positive or negative, as the reaction could be exothermic or endothermic.

Hence, the answer is option (3).

Approach to Solve Questions of Class 11 Chemistry Chapter 5 Thermodynamics

Thermodynamics comes under physical chemistry. This chapter is about learning the concepts and then applying them to solve the numerical.

Here are a few tips that help students to solve the questions with a good approach:

(1) Firstly, understand the key concepts:

• system
• surrounding
• internal energy
• work
• heat
• enthalpy
• Laws of Thermodynamics

2). Before solving any question, first give it a thorough reading and note down all the information given in the question.

• Identify given data like pressure, volume, temperature, etc.
• What needs to be found.

3). Use the appropriate formula based on the concept like:

$$\begin{array}{rl}& \mathrm{\Delta }U=q+W\\ & W=-P\mathrm{\Delta }V\text{ (work done at constant pressure) }\\ & \mathrm{\Delta }H=\mathrm{\Delta }U+P\mathrm{\Delta }V\\ & q=mc\mathrm{\Delta }T\text{ (in calorimetry) }\\ & \mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S\end{array}$$

4). Be careful while dealing with units and convert them if necessary to ensure consistency.

• temperature in Kelvin
• volume in litres

5). Practice again and again as it will helps in mastering thermodynamics numerically.

• Start with simpler problems
• Then gradually move to ones involving concepts like enthalpy change, work in isothermal or adiabatic processes, and heat capacity.

6). Solve NCERT textbook and NCERT exampler questions.

7). Questions from the NCERT books are asked directly in the NCERT boards and other competitive exams. Do previous year questions from NEET and JEE to get used to question patterns.

NCERT Class 11 Notes Chapter-Wise

NCERT notes for each chapter of class 11 are given below

Subject Wise NCERT Exemplar Solutions

Subject Wise NCERT Solutions