Class 11 Chemistry Chapter 2 notes on Structure of Atom cover key topics such as historical atomic models (Dalton, Thomson, Rutherford, Bohr), the quantum mechanical model, quantum numbers (n, l, m, s), electron configuration rules, orbital shapes, atomic spectra, and energy levels.
NCERT Class 11 Chemistry Chapter 2 Notes Structure of Atom - Download PDF
Everything in the universe is made up of atoms, from the tiniest drop of water to the vast universe. But can you imagine what an atom looks like? Can you see beyond that tiny structure? Well, some scientists did. This chapter Structure of Atom takes us on a trip to see the structure of that tiny atom which some brilliant scientists have already discovered, and some have even looked beyond the atoms, into the electrons, protons and neutrons.
This Story also Contains
- NCERT Notes for Class 11 Chemistry Chapter 2 Download PDF
- NCERT Notes for Class 11 Chemistry Chapter 2 Structure of Atom
- Structure of Atoms Previous Year Questions with Answers
- How to Master Class 11 Chemistry Chapter 2 Structure of Atom
- Advantages of Using Class 11 Chemistry Chapter 2 Structure of Atom Notes
- NCERT Class 11 Notes Chapter-Wise
- NCERT Solutions for Class 11 Chemistry
- NCERT Exemplar Class 11 Solutions Subject-wise
- NCERT Solution subject-wise
NCERT Class 11 Chemistry Chapter 2 Notes Structure of Atom contains concepts like atomic theories, quantum numbers, photoelectric effect etc., that are too crucial to understand. The NCERT notes for Class 11 Chemistry acts as a key guide to grasp these concepts effectively. These notes offer a structured approach to help you excel in your exams. The atomic models like the Thomson model of atom, the Rutherford model, and the Bohr model of atom are well explained in the notes. We have also included formulas and diagrams to provide you a clear picture. Follow these notes for feasible learning!
NCERT Notes for Class 11 Chemistry Chapter 2 Download PDF
These class 11 chemistry chapter 2 structure of atom notes cover all the key concept of this chapter to help students in quick revision before exam. You can download NCERT notes of this chapter from the button given below:
Also read
NCERT Notes for Class 11 Chemistry Chapter 2 Structure of Atom
The notes of this chapter contain all the concepts in detail that will be enough for you to attempt the questions. The structure of atom class 11 chemistry chapter 2 CBSE notes discussed here will help you visualise the concepts and the formulas will help you tackle the numericals.
2.1 Discovery of sub-atomic particles
The structure of the atom was obtained from the experiments on electrical discharge through gases.
2.1.1 Discovery of electron
The discovery of the electron began with Michael Faraday's work in the 1830s, where he found that electricity passing through solutions caused chemical changes, suggesting that electricity has tiny particles.
Later, in the 1850s, scientists studied electrical discharges in partially evacuated cathode ray tubes. These glass tubes had metal plates (electrodes) inside, and when high voltage was applied at low pressure, a stream of particles moved from the negative electrode (cathode) to the positive electrode (anode) - these were called cathode rays. When these rays passed through a hole in the anode and hit a zinc sulphide screen, they created a glowing spot, showing the presence of particles, which were later identified as electrons. Students can also follow NCERT Solutions for Class 11 Chemistry Chapter 2 to understand these concepts better through a series of solved questions.
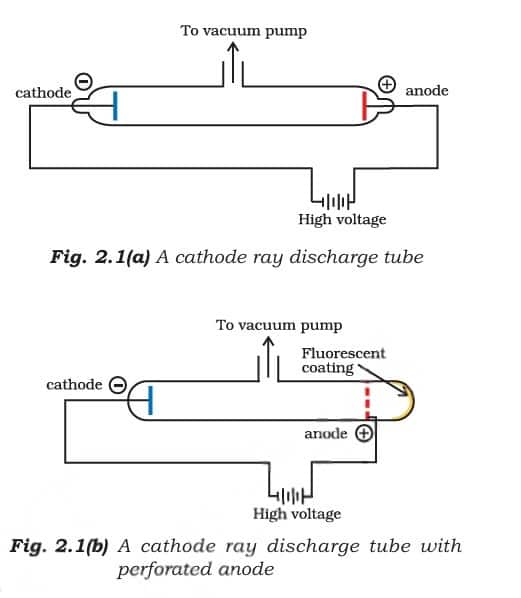
Properties of Cathode Rays
-
They travel in a straight line.
-
Cathode rays begin from the cathode and then move towards the anode.
-
They are invisible but can be made visible with the help of materials like fluorescent or Phosphorescent.
-
Since under the supply of electric charge, they are moved to the positive charge, which indicates that cathode rays consist of negatively charged particles.
-
The properties of cathode rays do not depend upon the material of the electrode in which it is used and the nature of gases that are present in the cathode ray tube.
2.1.2 Charge-to-mass ratio of an electron
Experimentally, J.J. Thomson determined the charge-to-mass ratio of the electrons. According to Thomson’s experiment, the amount of deviation for a particle from its path under the presence of an electric and a magnetic field depends upon
-
Deflection tends to be higher when the magnitude of the charge is higher for the particles.
-
When the mass of a particle is lighter, the deflection will be greater.
-
With the increase of voltage across the electrodes for with the increase of the strength of the magnetic field the deflection of electrons will also rise.
Thomson determined the value,
$\frac{e}{m_e}=1.758820 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1}$
Where the me is the mass of the electron and e is the magnitude of charge.
2.1.3 Charge on the electron
The oil drop experiment conducted by R.A. Millikan found the charge on the electron.
Charge of an electron=-1.6022×10-19C
Mass of electron = 9.1094×10-31kg
2.1.4 Discovery of Protons and Neutrons
Goldstein conducted another experiment with the help of a perforated cathode ray tube. A new type of eraser passes through the perforation of the card order by reducing the pressure, and it moves in just the opposite direction to that of the cathode rays. These are named canal rays or anode rays.
Properties of anode rays
-
The magnitude of the positive charge of anode rays depends upon the nature of the gas that is present in the tube.
-
It also depends on the gas for the value of the charge-to-mass ratio.
-
The behavior of anode rays is just the opposite of cathode rays and the magnetic and electric fields.
The smallest and lightest positive ion was obtained from hydrogen and was called a proton. This positively charged particle was characterised in 1919.
Later, the neutral particles were discovered by Chadwick (1932) by bombarding a thin sheet of beryllium with α-particles. When electrically neutral particles having a mass slightly greater than that of protons were emitted. He named these particles as neutrons.
2.2 Atomic Models
A series of atomic models were introduced that led to the discovery of atoms and their subatomic particles. You can also download the structure of atom ncert notes pdf for this topic to study anytime and anywhere.
|
Name |
Symbol |
Absolute Charge (C) |
Relative Charge |
Mass (kg) |
Mass (u) |
Approx. Mass (u) |
|
Electron |
e |
–1.602176 × 10⁻¹⁹ |
–1 |
9.109382 × 10⁻³¹ |
0.00054 |
0 |
|
Proton |
p |
+1.602176 × 10⁻¹⁹ |
+1 |
1.6726216 × 10⁻²⁷ |
1.00727 |
1 |
|
Neutron |
n |
0 |
0 |
1.674927 × 10⁻²⁷ |
1.00867 |
1 |
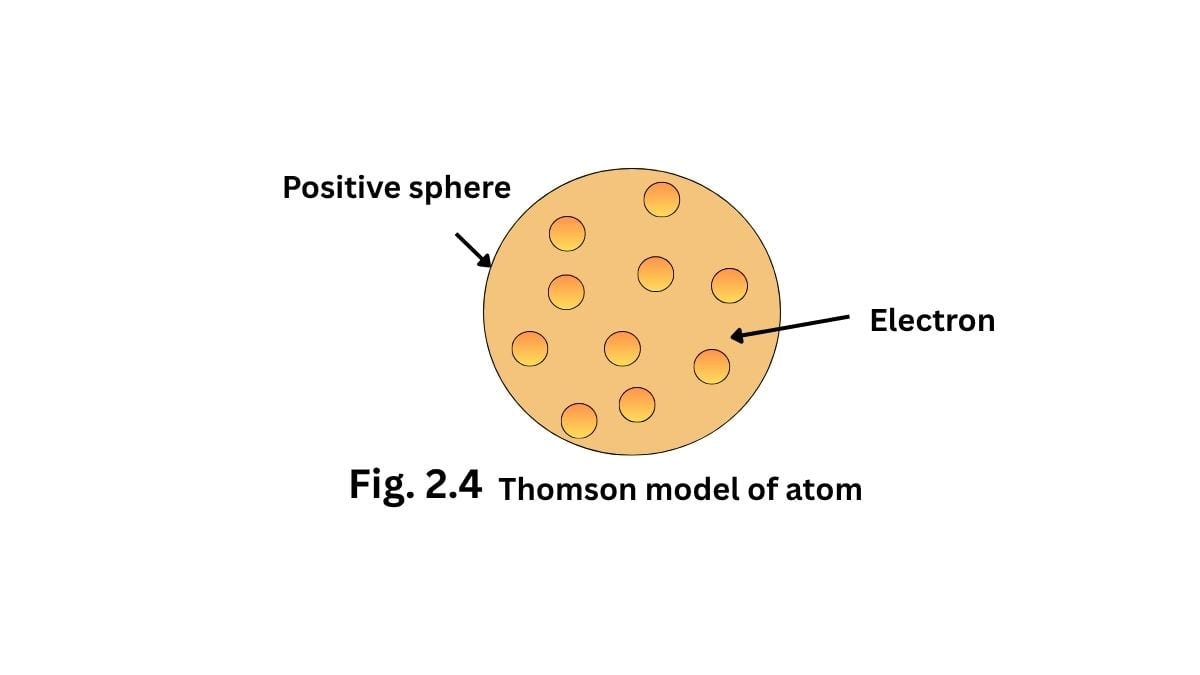
2.2.1 Thomson model of atom
J.J. Thomson proposed a structure for an atom that can be regarded as a sphere of an approximate radius carrying a positive charge due to protons, and in which the negatively charged electrons are embedded. Thereby, the atom can be visualized as a pudding for a cake of positively charged protons with electrons in it. And the mass of atoms is evenly spread over the atom.
2.2.2 Rutherford’s nuclear model of atom
Rutherford's $\alpha$-scattering experiment
A stream of high energy α–particles from a radioactive source was directed at a thin foil (thickness ∼ 100 nm) of gold metal. The thin gold foil had a circular fluorescent zinc sulphide screen around it. Whenever α–particles struck the screen, a tiny flash of light was produced at that point

Observations of Rutherford's experiment:
- Most of the α-particles passed through the gold foil undeflected indicating that most of the atom is empty space.
- A small fraction of the α–particles was deflected by small angles indicating that the postive charge is concentrated in a very small volume.
- Very few α–particles (∼1 in 20,000) bounced back, that is, were deflected by nearly 180°, thus confirming the size of the nucleus to be very small.
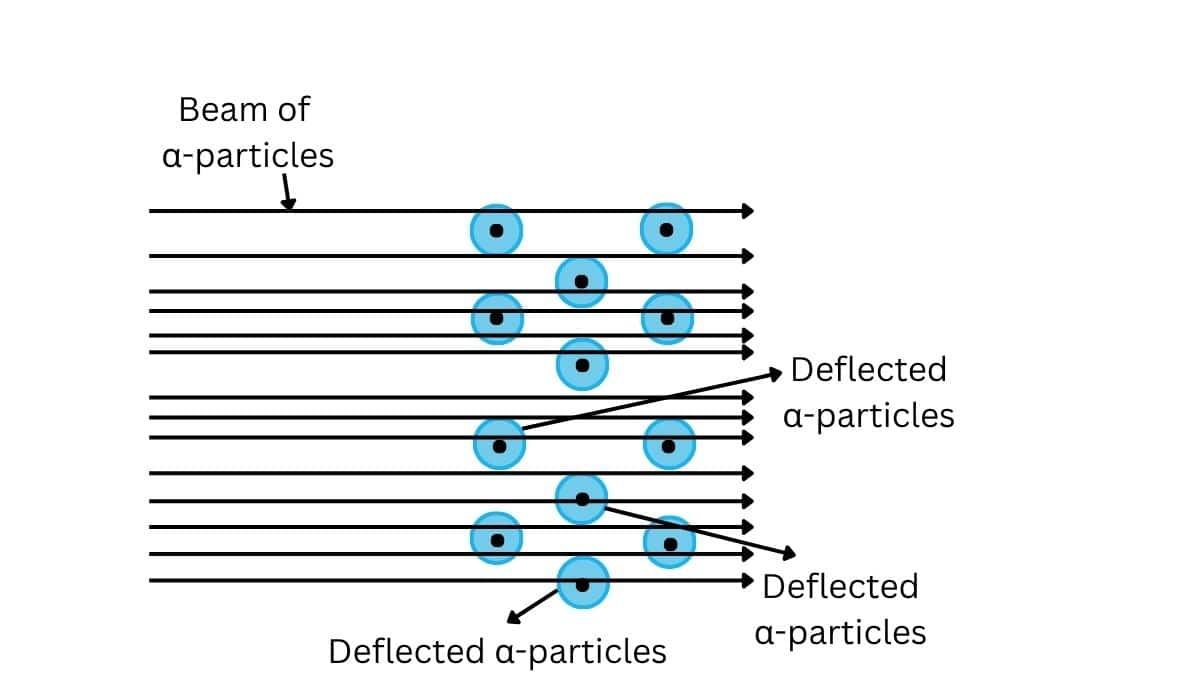
The observations of the Rutherford Alpha scattering experiment are
-
Most of the part of the atom is empty and atom is spherical in shape.
-
Each atom consists of a small, heavy, positively charged portion located at the centre, known as nucleus.
-
All positive charges of an atom (i.e protons) are present in the nucleus and electrons move around the nucleus in circular orbits.
-
Electrons and the nucleus are held together by electrostatic forces of attraction.
2.2.3 Atomic number and mass number
Atomic Number
The number of protons present in the nucleus is referred to as the atomic number. For example, the number of protons in a sodium atom is 11 and also the atomic number of sodium is 11. For maintaining electrical neutrality the number of electrons in an atom is equal to the number of protons.
Mass Number
The sum of the number of protons and neutrons present in a nucleus together is called the mass number.
2.2.4 Isobars and isotopes
The element that has the same atomic number but a different mass number is an isotope. 1H1, 1H2, 1H3.
And the element that is processing the same mass number but a different atomic number is an isobar. 6C14, 7N14.
2.2.5 Drawbacks of Rutherford model
- According to Maxwell's theory, a moving charged particle under acceleration radiates energy and thus the electron must spiral into the nucleus, but that does not occur. The stability of the atom was not explained by the Rutherford's model.
- Rutherford's model does not provide any information about the position of the electron or its energy.
2.3 Developments leading to Bohr’s model of atom
Historically, results obtained from studies of radiation interactions with matter have yielded enormous information about the structure of atoms and molecules. Niels Bohr used these findings to refine the model presented by Rutherford. Two developments played a major role in the formulation of Bohr’s model of atom.
-
Radiation causes wavelike and particle-like properties, which means that it has a dual character
-
The atomic spectra can be explained only by assuming the quantum state electronic energy levels in atoms.
2.3.1 Wave nature of electromagnetic radiation
Electromagnetic radiation -
According to electromagnetic wave theory, energy is emitted continuously from a source in the form of radiation (or waves), known as electromagnetic radiation. Electromagnetic radiations have both magnetic field as well as electric field components which oscillate in the phase perpendicular to each other as well as perpendicular to the direction of wave propagation. These waves do not require any medium for propagation and can propagate through a vacuum. There are many types of electromagnetic radiations which constitute what is known as the electromagnetic spectrum. There are several parameters required to characterise or define a wave. These parameters are defined below:
1. Wavelength ($\lambda$): It is the distance traveled by the wave during one complete oscillation
The maxima are called as Crests and the minima are called as Troughs. Alternatively, the distance between two consecutive crests or two consecutive troughs is also called as the wavelength.
2. Time Period (T): It is the time required for one complete oscillation or one complete cycle by a wave.
3. Frequency ($\nu$): It is number of waves produced by the source in one second. It is the inverse of the time period. Its SI unit is Hertz (Hz).
$\nu=\frac{1}{\mathrm{~T}}$
4. Speed (c): It is the distance travelled by the wave in one second. In one time period, the wave travels a distance equal to its wavelength.
$\mathrm{c}=\frac{\text { distance }}{\text { time }}=\frac{\text { Wavelength }}{\text { Time Period }}=\frac{\lambda}{\mathrm{T}}$
$\because \nu=\frac{1}{\mathrm{~T}}$
$\therefore c=\nu \times \lambda$
The speed of all the different components of light is the same i.e. they travel with the speed of 3 $\times$ 108 m/s. Their frequency and wavelength are different
5. Wave number ($\bar{\nu}$) : It is the inverse of the wavelength. It can also be defined as the number of wavelengths present in unit length.
$\bar{\nu}=\frac{1}{\lambda}$

The rays present on the left extreme of the spectrum have the greatest frequency, the least wavelength, and the greatest energy. As the frequency increases, wavelength decreases and the energy increases.
2.3.2 Particle nature of electromagnetic radiation: Planck’s Quantum theory
-
Max Planck put forward a theory for explaining the phenomenon of blackbody radiation and the photoelectric effect. The theory focuses on
-
The radiant energy absorbed or emitted is in the form of small pockets of energy and these small pockets of energy are quantum.
-
The energy of each Quantum is directly proportional to the frequency of the radiation emitted.
The ideal body that has the ability to emit and absorb all frequencies is a black body. And the corresponding radiation emitted by a black body is black body radiation.
$E=h \nu=\frac{h c}{\lambda}$
where h is Planck's constant and it has a value equal to 6.63 $\times$ 10-34 J-s
Photoelectric Effect
When a beam of light passes on the surface of some metals, electrons are emitted from the metal surface. This phenomenon is the photoelectric effect. And it has been observed that only photons of light of a particular frequency, that is the threshold frequency, can cause the photoelectric effect. The kinetic energy of the electron emitted from the surface of the metal is directly proportional to the frequency of the striking photons. And also when the intensity of the photon of the light is increasing, more electrons are ejected.
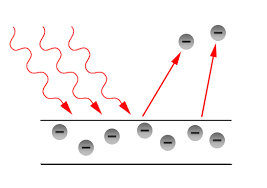
There were certain observations in the photoelectric effect experiment.
(1) There was a requirement of a minimum energy for each metal for the photoelectric effect to occur. This minimum energy is known as work function (W0) and it can be closely associated with the ionisation energy of the metal.
- Corresponding to the work function, there is a minimum frequency of light required for the photoelectric effect. This minimum frequency is called as Threshold frequency.
- Corresponding to the work function, there is a maximum wavelength of incident light above which the photovoltaic effect cannot occur. This maximum wavelength is called Threshold wavelength.

Mathematically, the work function, threshold frequency and threshold wavelength can be associated as
$\mathrm{W}_0=\mathrm{h} \nu_0=\frac{\mathrm{hc}}{\lambda_0}$
Note: hc is approximately equal to 2 x 10-25 J-m or 12400 eV-nm. (eV is the energy in electron volts)
(2) The number of electrons ejected is proportional to the intensity (brightness) of light striking the metal, but does not depend upon the frequency of light.
(3) There was almost no time lag between the striking of light and ejection of photo electrons
(4) The kinetic energy of the ejected electrons (photoelectrons) depends upon the frequency of the light used.
Einstein's photoelectric equation
From conservation of energy
$\begin{gathered}E_p=W_0+K E \\ \therefore h \nu=h \nu_0+\frac{1}{2} m v^2\end{gathered}$
where m is the mass of the electron and v is the velocity associated with the ejected electron. Also, h is Planck’s constant and v0 is threshold frequency of metal.
(5) The Kinetic energy of ejected photoelectron is also sometimes associated with Stopping Potential. It is defined as the minimum opposing potential applied due to which the kinetic energy of electron becomes zero.
$\frac{1}{2} m v^2=e V_s$
where,
Vs = Stopping potential
e = Charge on electron
Dual behavior of Electromagnetic Radiation
Light and other electromagnetic radiation consist of a dual nature. That is, they have particle and wave-like properties. Radiations emitted by the matter show the properties of a particle by exhibiting propagation. Electrons also exhibit wave-particle duality.
2.3.3 Evidence for the quantized* electronic energy levels: Atomic spectra
When a light ray passes through a prism the wave which is having a short wavelength forms a colored band more than the one that has a longer wavelength. These bands then spread to form a series of colored bands and are called the spectrum. The one that is deviated least is the one which is having the longest wavelength, that is, their red color.
Continuous spectrum
When white light is passed through a prism, it will split into seven different colored bands, just like a rainbow and these colors are continuous and it is called the continuous spectrum.
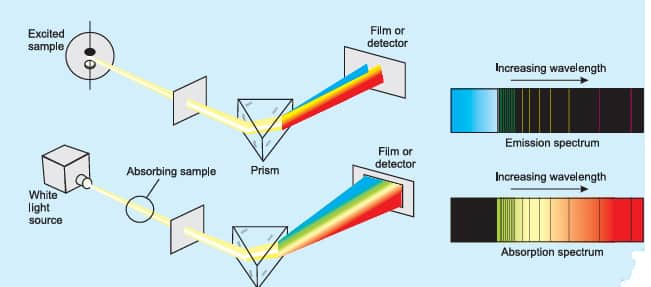
Emission spectra
When radiation is emitted from a source and is then passed to a prism, which is then received on a photographic plate it is called the emission spectrum. The emission spectrum can be observed by heating a substance to a high temperature.
Line spectra
The emission spectra of atoms in the gas phase do not show a continuous spread of wavelength from red to violet, rather they emit light only at specific wavelengths with dark spaces between them. Such spectra are called line spectra or atomic spectra because the emitted radiation is identified by the appearance of bright lines in the spectra. Sodium emits yellow light while potassium emits violet light.
Absorption spectra
A ray of light, when allowed to pass through the vapors of a substance and the transmitted light is then allowed to strike a prism, dark lines appear. The dark line represents that the radiations corresponding to them are absorbed by the substance. The spectrum is called the absorption spectrum.
The figure below is showing absorption and emission spectra.
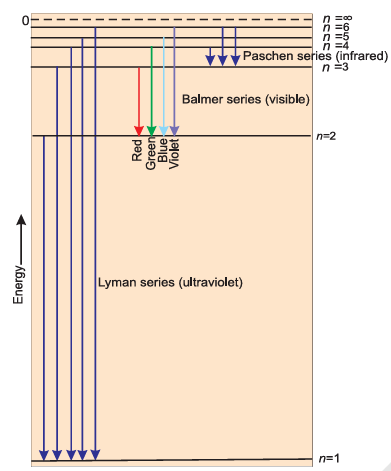
Line Spectrum of Hydrogen
When an electric discharge is passed through gaseous hydrogen, the H2 molecules dissociate, and the energetically excited hydrogen atoms produced emit electromagnetic radiation of discrete frequencies. The spectrum, consisting of a large number of lines, is obtained and the spectrum is called the hydrogen spectrum. The series of lines is named as the Lyman series, Balmer series, Paschen series, Brackett series, and Pfund series.
2.4 Bohr’s Model for Hydrogen atom
1. The electron in the hydrogen atom can move around the nucleus in a circular path of fixed radius and energy. These paths are called orbits, stationary states, or allowed energy states and are arranged concentrically around the nucleus. The force of attraction between the nucleus and an electron provides the centripetal force required by the electron to carry out the circular motion.
2. The energy of an electron in the orbit does not change with time. However, the electron will move from a lower stationary state to a higher stationary state when a required amount of energy is absorbed by the electron or energy is emitted when the electron moves from a higher stationary state to a lower stationary state
3. Energy can be absorbed or emitted when electron transitions between two different orbits and the frequency of the photon involved can be calculated using the formula:
$\left|E_1-E_2\right|=h \nu$
4. The angular momentum of an electron is quantised. In a given stationary state, it can be expressed as
L= mvr= nh/2$\pi$, n = orbit number
So, only those energy states (or orbits) are allowed in which the above equation holds true for the angular momentum.
Note: Bohr's model is only valid for hydrogen-like species or unielectronic species that contain only a single electron
2.4.1 Explanation of line spectrum of Hydrogen
The line spectrum of the hydrogen atom can be explained using Bohr's model, which says that electrons absorb or emit energy when they jump between orbits (energy levels). When an electron moves from a lower orbit (ni) to a higher one (nf), energy is absorbed. When it moves from a higher orbit to a lower one, energy is emitted as light. The energy difference between two levels is given by:
$
\Delta E=E_f-E_i=-R_H\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)
$
Where $R_H=2.18 \times 10^{-18} \mathrm{~J}$ is the Rydberg constant. The frequency of light emitted or absorbed is:
$
\nu=\frac{\Delta E}{h}
$
And the wavenumber (lines in the spectrum) is
$
\bar{v}=R\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right)
$
This formula matches the one given by Rydberg earlier using experimental data. Each spectral line in hydrogen corresponds to a specific electron transition. In a large sample of hydrogen atoms, many such transitions occur, producing multiple lines. The brightness of a line depends on how many photons of the same energy are emitted or absorbed.
2.4.2 Limitations of Bohr’s model
It fails to account for the finer details (doublet, that is, two closely spaced lines) of the hydrogen atom spectrum observed by using spectroscopic techniques.
This model is also unable to explain the spectrum of atoms other than hydrogen, for example, He.
Further, Bohr’s theory was also unable to explain the splitting of spectral lines in the presence of a magnetic field (Zeeman effect) or an electric field (Stark effect). It could not explain the ability of atoms to form molecules by chemical bonds.
2.5 Towards Quantum mechanical model of atom
Two important developments that contributed significantly to the formulation of such a model are
- Dual behaviour of matter.
- Heisenberg uncertainty principle
2.5.1 Dual behaviour of matter
The scientist de-Broglie proposed that just like light, matter should exhibit both particle and wave-like properties. This means that just as the photon has momentum as well as wavelength, electrons should also have momentum as well as wavelength, and he proposed the following mathematical relationship
$\lambda=\frac{h}{m v}=\frac{h}{p}=\frac{h}{\sqrt{2 m K E}}=\frac{h}{\sqrt{2 m q V}}$
where m is the mass of the particle, v is its velocity, p is the momentum, and K.E. is the Kinetic Energy of the particle.
V is the voltage across which the charged particle having charge q is accelerated.
(2) de Broglie’s prediction was confirmed experimentally when it was found that an electron beam undergoes diffraction, a phenomenon characteristic of waves.
(3) It needs to be noted that, according to de Broglie, every object in motion has a wave character. This wavelength is quite significant for the subatomic particles, which have very small masses. The wavelengths associated with ordinary objects are however so short that their wave properties cannot be detected as they have large masses.
2.5.2 Heisenberg’s Uncertainty Principle
It states that it is impossible to determine simultaneously the exact position and exact momentum (or velocity) of an electron.
If an attempt is made to ensure that any one of these two quantities is measured with a higher accuracy, then the other quantity becomes less accurate.
Mathematically, the product of uncertainty in position(Δx) and uncertainty in momentum(ΔP) is equal to or greater than h/4π
$\Delta x . \Delta P \geq \frac{h}{4 \pi}$
It can be proved mathematically that the uncertainty principle is only significant for subatomic particles but not for large-sized objects.
2.6 Quantum mechanical model of atom
-
Theoretical science that deals with the study of the motion of microscopic objects that have both particle-like and wave-like properties.
-
The energy of an electron in an atom is in a quantized state.
-
The existence of quantised electronic energy levels is a direct result of the wave-like properties of electrons and are allowed solutions of the Schrödinger wave equation.
-
The exact position and exact velocity of an electron in an atom cannot be found out simultaneously.
-
An atomic orbital is the wave function ψ for an electron in an atom.
-
The square of the orbital wave function |ψ|2 is the probability of finding an electron.
For a system (such as an atom or a molecule whose energy does not change with time), the Schrödinger equation is written as $\hat{H} \Psi=E \Psi$, where $\hat{H}$ is a mathematical operator called the Hamiltonian.
2.6.1 Orbitals and Quantum Numbers
As the atomic energy levels or the orbits are quantized, they can be expressed in terms of quantum numbers. Quantum numbers are;
- Principal
- Azimuthal
- Magnetic
- Spin
Principal quantum number(n)
It represents the principal shell of an atom. It can have integral values except zero, like 1,2,3,.... Also denoted as K, L, M, etc.
The maximum number of electrons in a principal shell can be 2n2, where n is the principal quantum number.
This quantum number gives information about :
- Distance of electron from nucleus i.e., size of electron cloud.
- Energy of an electron in any shell
$\mathrm{E}_{\mathrm{n}}=-\frac{1312 \times \mathrm{Z}^2}{\mathrm{n}^2} \mathrm{~kJ} / \mathrm{mol}$
Where Z is the atomic number and n is the principal quantum number.
Azimuthal quantum number(l):
The azimuthal quantum number represents the subshell or subenergy shell in an atom.
l has values from 0 to (n-1).
For eg: for n = 2 ; l = 0, 1
Subshell notation for 0, 1 is s and p.
No. of electrons [2(2l+1)]: for s subshell l = 2; for p subshell, l = 6.
Magnetic quantum number(m):
It represents the number of orbitals present in a subshell.
m has values ranging from -l to +l, including zero.
For eg, for ‘s’ subshell :
-
The value of l is 0
-
m has value = 0
For ‘p’ subshell :
-
The value of l is 1
-
m has value -1, 0, +1
Spin quantum number(s):
Electrons in an orbital can spin either clockwise or anticlockwise.
Thus, an electron can have only two possible values of this quantum number, either $+\frac{1}{2}$ or $-\frac{1}{2}$ respectively.
2.6.2 Shapes of atomic orbitals
According to the German physicist, Max Born, the square of the wave function (i.e.,ψ 2) at a point gives the probability density of the electron at that point.
The region where this probability density function reduces to zero is called nodal surfaces or simply nodes.
Shape of s orbital: spherical
In general, it has been found that the ns-orbital has (n – 1) nodes, that is, the number of nodes increases with the increase of principal quantum number n.

Shape of p orbital: Dumb-bell

Shape of d orbital: Double Dumb-bell

The total number of nodes are given by (n–1), i.e., sum of l angular nodes and (n – l – 1) radial nodes.
2.6.3 Energies of orbitals
The orbitals having the same energy are called degenerate. The 1s orbital in a hydrogen atom, as said earlier, corresponds to the most stable condition and is called the ground state and an electron residing in this orbital is most strongly held by the nucleus.
An electron in the 2s, 2p or higher orbitals in a hydrogen atom is in an excited state.
Within a given principal quantum number, the energy of orbitals increases in the order $s<p<d<f$. For higher energy levels, these differences are sufficiently pronounced and staggering of orbital energy may result, e.g., $4 s<3 d$ and $6 s<5d ; 4 f<6 p$.
2.6.4 Filling of orbitals in atom
Aufbau Principle -
According to this rule, “orbitals are filled in the increasing order of their energies starting with the orbital of lowest energy”. Energy of various orbitals are compared with (n+l) rule.
The orbitals having a lower value of (n+l), has lower energy.
If the value of (n+l) is the same for two orbitals, then the orbital with the lower value of ‘n’ would have lower energy and be filled first.
For eg: 3p and 3d.
For 3p : n=3, l=1 so n+l= 4
For 3d : n=3, l=2 so n+l=5. Thus energy of 3p is lower than that of 3d.

Pauli Exclusion Principle -
“No two electrons in an atom can have the same set of four quantum numbers".
Hund’s Rule of Maximum Multiplicity -
The pairing of electrons in the orbitals belonging to the same subshell ( p,d, or f ) does not take place until each orbital belonging to that subshell has got one electron each i.e. it is singly occupied.
2.6.5 Electronic Configuration of Atoms
Writing of electronic configuration of any element is based on three rules. They are:
-
Aufbau principle
-
Pauli’s exclusion principle
-
Hund’s rule of maximum multiplicity
The distribution of electrons into orbitals of an atom is called its electronic configuration.
The electronic configuration of the different elements can be represented in two ways:
-
Subshell notation
-
Orbital diagram
Let’s understand with the help of examples:
The hydrogen atom has only one electron, which goes in the orbital with lowest energy, namely 1s. The E.C. of hydrogen is 1s1 (subshell notation)

The electronic configuration of lithium is 1s2 2s1. Lithium has 3 electrons as its atomic number is 3. 2 electrons are filled in the 1s orbital, and 1 electron is filled in the 2s orbital.
let us consider fluorine (Z = 9) :
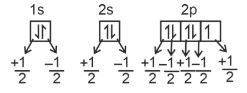
F(Z = 9) = 1s2, 2s2, 2px2, 2py2, 2pz1 or

The importance of knowing the exact electronic configuration of an element lies in the fact that the chemical properties of an element are dependent on the behavior and relative arrangement of its electrons.
2.6.6 Stability of completely filled and half-filled subshells
The completely filled or half-filled subshells have a symmetrical distribution of electrons in them and are therefore more stable.
Symmetrical distribution of electrons: It is well known that symmetry leads to stability. The completely filled or half-filled subshells have a symmetrical distribution of electrons in them and are therefore more stable.
Exchange Energy: The stabilizing effect arises whenever two or more electrons with the same spin are present in the degenerate orbitals of a subshell. These electrons tend to exchange their positions and the energy released due to this exchange is called exchange energy. The number of exchanges that can take place is maximum when the subshell is either half-filled or completely filled. As a result, the exchange energy is maximum and so is the stability.
For example, the valence electronic configurations of Cr and Cu are $3 d^5 4 s^1$ and $3 d^{10} 4 s^1$ respectively and not $3 d^4 4 s^2$ and $3 d^9 4 s^2$.
Structure of Atoms Previous Year Questions with Answers
Here, you will find previous year questions with answers from the chapter 2, covering important concepts, exam-focused topics, and key chemistry keywords. The concepts used to solve these questions are explained in structure of atom class 11 chemistry chapter 2 CBSE notes.
Question 1: The extra stability of a half-filled subshell is due to
(A) Symmetrical distribution of electrons
(B) Smaller coulombic repulsion energy
(C) The presence of electrons with the same spin in non-degenerate orbitals
(D) Larger exchange energy
(E) Relatively smaller shielding of electrons by one another
Identify the correct statements
(1) (B), (D) and (E) only
(2) (A), (B), (D) and (E) only
(3) (B), (C) and (D) only
(4) (A), (B) and (D) only
Answer: The extra stability of a half-filled subshell is due to the symmetrical distribution of electrons, smaller coulombic repulsion, larger exchange energy, and smaller shielding of electrons.
Hence, the correct answer is option (2).
Question 2: Which one of the following about an electron occupying the 1s orbital in a hydrogen atom is incorrect? (Bohr's radius is represented by $\mathrm{a}_0$ )
(1). The probability density of finding the electron is maximum at the nucleus
(2) The electron can be found at a distance $2a_0$ from the nucleus
(3) The 1s orbital is spherically symmetrical
(4) The total energy of the electron is maximum when it is at a distance $\mathrm{a}_0$ from the nucleus
Answer:
1. $\Psi^2=$ Probability density is maximum at the nucleus. Hence, statement 1 is true
2. Electrons can exist up to infinity from the nucleus. Hence, statement 2 is true.
3. The 1s orbital is spherically symmetrical- it is true
4. The energy of an electron is maximum at an infinite distance from the nucleus.
More further the electron is from the nucleus, the more is its energy. The total energy of an electron is given by $-\frac{13.6 z^2}{n^2}$.
So as $n \uparrow \Rightarrow$ energy $\uparrow$
Hence, statement 4 is false.
Hence, the correct answer is option (4).
Question 3: Which of the following sets of quantum numbers are correct?
n l m1
(i) 1, 1, +2
(ii) 2, 1, +1
(iii) 3, 2, -2
(iv) 3, 4, -2
Choose from the options given below
1) (i) and (ii)
2) (ii) and (iii)
3) (ii) and (iii)
4) (i) and (iv)
Answer:
As in the case n = 1, then I ≠ 1, therefore option (i) is incorrect.
In case n = 3, I ≠ 4, therefore option (iv) is also incorrect.
In case n = 2, I = 0, 1. When l = 1, then m = -1, 0, +1. Therefore, option (ii) is correct.
In case n = 3, l = 0, 1, 2. When l = 2, m = -2, -1, 0, +1, +2. Therefore, option (iii) is also correct.
Hence, the correct answer is option (2).
Question 4: The energy of an electron in first Bohr orbit of H -atom is -13.6 eV . The magnitude of energy value of electron in the first excited state of $\mathrm{Be}^{3+}$ is _______eV . (nearest integer value)
(1) 96
(2) 54
(3) 55
(4) 65
Answer:
$\begin{aligned} & \mathrm{E}_1 \text { of } \mathrm{H} \text {-atom }=-13.6 \mathrm{eV} \\ & \begin{aligned} \mathrm{E}_2 \text { of } \mathrm{Be}^{3+} & =\frac{-13.6 \times \mathrm{Z}^2}{\mathrm{n}^2} \\ = & \frac{-13.6 \times(4)^2}{(2)^2} \\ = & -54.4 \mathrm{eV} \\ \left|\mathrm{E}_2\right| \text { of } \mathrm{Be}^{3+} & =54 \mathrm{eV}\end{aligned}\end{aligned}$
Hence, the answer is option (2).
Question 5: Correct statements for an element with atomic number 9 are
A. There can be 5 electrons for which $\mathrm{m}_{\mathrm{s}}=+\frac{1}{2}$ and 4 electrons for which $\mathrm{m}_{\mathrm{s}}=-\frac{1}{2}$
B. There is only one electron in $p_z$ orbital
C. The last electron goes to orbital with $\mathrm{n}=2$ and $l=1$
D. The sum of angular nodes of all the atomic orbitals is 1 .
Choose the correct answer from the options given below:
(1) C and D Only
(2) A and C Only
(3) A, C and D Only
(4) A and B Only
Answer:
$Z=9$
Electronic configuration $\Rightarrow$
- There can be $5 \mathrm{e}^{-}$for which $\mathrm{m}_{\mathrm{s}}=+\frac{1}{2}$
and $4 \mathrm{e}^{-}$for which $\mathrm{m}_{\mathrm{s}}=-\frac{1}{2}$
- There can be $2 \mathrm{e}^{-}$in $\mathrm{p}_{\mathrm{z}}$ orbital
- Last $e^{-}$enters $2 p(n=2, l=1)$
- Angular nodes $=1$
Sum of angular nodes
- $1 \mathrm{~s}(\mathrm{l}=0) \rightarrow 0$
- $2 \mathrm{~s}(\mathrm{l}=0) \rightarrow 0$
$2 \mathrm{p}(\mathrm{l}=1) \rightarrow$ each has 1 angular node $\times 3$ orbitals $\rightarrow 3$ angular nodes
$\therefore$ Sum of angular nodes $=0+0+3=3$
Hence, the correct answer is option (2).
How to Master Class 11 Chemistry Chapter 2 Structure of Atom
In order to master this chapter a clear understanding of atomic models and electron arrangements is must. These class 11 chemistry chapter 2 structure of atom notes help to understand the basic concepts from your NCERT textbook.
- Students need to understand the basic atomic models like with Dalton’s, Thomson’s, Rutherford’s, and Bohr’s models and their postulates, limitations, and contributions.
- After that learn about the basics of quantum mechanics like quantum numbers, orbitals, and the significance of each number (n, l, m, s).
- Questions related to electronic configurations for elements and their exceptions are often asked in exams. Students can refer to the structure of atom class 11 chemistry chapter 2 CBSE notes for better understanding of these concepts.
- Topics like line spectra, hydrogen spectrum, and energy transitions play an important role in this chapter, understand them carefully.
- Solve maximum questions on energy levels, wavelengths, and frequencies of radiation, Bohr’s radius, energy of electron, and Rydberg equation.
- At last students can solve previous year questions from this chapter.
Advantages of Using Class 11 Chemistry Chapter 2 Structure of Atom Notes
The structure of atom ncert notes cover all important concepts from the NCERT book in a simple and organised manner. The advantages of using these notes are given below:
- Students can refer to these notes to understand the topics like atomic models, quantum numbers, and electron configurations.
- These notes are very helpful for revision before exams or understanding the concepts.
- The ncert class 11 chemistry chapter 2 structure of atom notes include all important topics like Bohr’s model, dual nature of matter, and Heisenberg’s uncertainty principle.
- These notes provide explanations and solved examples that help students to understand the concepts easily.
- They are prepared by subject experts in a very clear and comprehensive manner and are helpful in both CBSE boards and competitive exams.
NCERT Class 11 Notes Chapter-Wise
Along with ncert class 11 chemistry chapter 2 structure of atom notes. Follow the links below and get access to the NCERT notes for Class 11 of other chapters.
NCERT Solutions for Class 11 Chemistry
Along with class 11 chemistry chapter 2 structure of atom notes, follow the links below to get chapter-wise solutions of NCERT and make your learning better.
NCERT Exemplar Class 11 Solutions Subject-wise
Students can refer to the links given below for the NCERT exemplar subject-wise solutions
NCERT Solution subject-wise
Students can also follow NCERT solutions for other subjects to ace their exam preparations. Click on the link below
| NCERT Solutions for Class 11 Maths |
| NCERT Solutions for Class 11 Physics |
| NCERT Solutions for Class 11 Chemistry |
| NCERT Solutions for Class 11 Biology |
Frequently Asked Questions (FAQs)
Electrons occupy energy levels, or shells, around the nucleus based on their energy. These levels are quantized, meaning electrons can only exist in these specific orbits. Each shell can hold a certain maximum number of electrons, and as electrons fill these levels, they follow the Aufbau principle, Hund's rule, and Pauli's exclusion principle.
Valence electrons are the electrons present in the outermost shell of an atom. They are crucial because they determine the chemical properties of an element and how it will react with other elements.
The main subatomic particles in an atom are protons, neutrons, and electrons. Protons are positively charged and located in the nucleus, while neutrons have no charge and also reside in the nucleus.
Yes, Class 11 Chemistry students should have free access to notes, as it helps them understand concepts clearly, revise efficiently, and prepare for exams without financial barriers.
The principal quantum number (n) describes the energy level or shell of an electron in an atom, with higher values of 'n' indicating higher energy levels and larger distances from the nucleus.
Heisenberg's Uncertainty Principle states that it is fundamentally impossible to determine simultaneously, and with absolute precision, both the position and the momentum (or velocity) of a subatomic particle like an electron. If you know the position very accurately, your knowledge of its momentum becomes uncertain, and vice versa. Mathematically: Δx ⋅ Δp ≥ h/4π.
Hund's Rule states that for a given subshell (orbitals of equal energy or degenerate orbitals, like the three p-orbitals or five d-orbitals), electrons will first occupy all the orbitals individually with parallel spins (same spin direction) before any orbital is doubly occupied (paired up). This maximizes the total spin multiplicity and leads to a more stable configuration.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters