NCERT Solutions for Class 11 Physics Chapter 14 Oscillations

Edited By Vishal kumar | Updated on Sep 07, 2023 12:02 PM IST

NCERT Solutions Class 11 Physics Oscillations – Download Pdf

NCERT Solutions for Class 11 Physics Chapter 14 Oscillations hold great significance in the Class 11 curriculum. On this Careers360 page of NCERT solutions , you'll find comprehensive ch 14 physics class 11 ncert solutions crafted by experts, presented in a clear and straightforward manner. This resource covers a total of 25 questions, encompassing exercises from 14.1 to 14.19, and 14.20 to 14.25 in the additional exercise section. The oscillation exercise class 12 solutions are conveniently available in PDF format, allowing students to access and download them for free whenever they require assistance.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

NEET Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | ALLEN

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

This Story also Contains

NCERT Solutions Class 11 Physics Oscillations – Download Pdf
NCERT Solutions for Class 11 Physics Chapter 14: Oscillations
NCERT Solutions For Class 11 Physics Chapter 14 Oscillations: Exercise Solution
NCERT solutions for class 11 physics chapter 14 oscillations: Additional Exercise Solution
oscillation class 11 physics
NCERT solutions for class 11 physics chapter-wise
Oscillations Class 11 NCERT Topics
Importance of NCERT Solutions for Class 11 Physics Chapter 14 Oscillations:
Key features of NCERT Solutions for Class 11 Physics Chapter 14
Subject wise NCERT Exemplar solutions

Problems with motion along a straight line, motion in a plane, projectile motion, etc. were discussed in the previous chapters. NCERT Physics chapter 14 Oscillations Class 11 solutions explains problems on periodic and oscillatory motions. The motion which repeats after a certain interval of time is called periodic motion. For example, the motion of a planet around the sun, the motion of pendulum of a wall clock etc are periodic. To and fro periodic motion about a mean position is known as oscillatory motion.

CBSE NCERT solutions for Class 11 Physics chapter 14 Oscillations have questions on simple harmonic motion (SHM). SHM is the simplest form of oscillatory motion. In SHM the force on the oscillating body is directly proportional to the displacement about the mean position and is directed towards the mean position. Oscillation chapter class 11 solution are an important tool to score well in the exams and also they are useful if you want to study other subjects of other classes as well. The concept studied in NCERT becomes easy to understand with the help of NCERT solutions for class 11.

This chapter has been renumbered as Chapter 13 in accordance with the CBSE Syllabus 2023–24.

Free download ch 14 physics class 11 ncert solutions PDF for CBSE exam.

NCERT Solutions for Class 11 Physics Chapter 14: Oscillations

Download PDF

NCERT Solutions For Class 11 Physics Chapter 14 Oscillations: Exercise Solution

Q. 14.1 Which of the following examples represent periodic motion?

(a) A swimmer completing one (return) trip from one bank of a river to the other and bank.

(b) A freely suspended bar magnet displaced from its N-S direction and released.

(d) An arrow released from a bow

Answer:

(a) The motion is not periodic though it is to and fro.

(b) The motion is periodic.

(d) The motion is not periodic.

Q. 14.2 Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?

(a) the rotation of earth about its axis.

(b) motion of an oscillating mercury column in a U-tube.

(c) motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most point.

(d) general vibrations of a polyatomic molecule about its equilibrium position.

Answer:

(a) Periodic but not S.H.M.

(b) S.H.M.

(d) Periodic but not S.H.M.M [A polyatomic molecule has a number of natural frequencies, so its vibration is a superposition of SHM’s of a number of different frequencies. This is periodic but not SHM]

Q .14.3 Fig. 14.23 depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?

1650449930218

Answer:

The x-t plots for linear motion of a particle in Fig. 14.23 (b) and (d) represent periodic motion with both having a period of motion of two seconds.

Q. 14.4 (a) Which of the following functions of time represent

(a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion ( $\omega$ is any positive constant):

(a) $sin\; \omega t-cos\; \omega t$

Answer:

$\\sin\omega t-cos\omega t\\ =\sqrt{2}\left ( \frac{1}{\sqrt{2}}sin\omega t-\frac{1}{\sqrt{2}}cos\omega t \right )\\ =\sqrt{2}(cos\frac{\pi }{4}sin\omega t-sin\frac{\pi }{4}cos\omega t)\\ =\sqrt{2}sin(\omega t-\frac{\pi }{4})$

Since the above function is of form $Asin(\omega t+\phi )$ it represents SHM with a time period of $\frac{2\pi }{\omega }$

Q. 14.4 (b) Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion ( $\omega$ is any positive constant):

(b) $sin^{3}\omega t$

Answer:

$\\sin3\omega t =3sin\omega t -4sin^{3}\omega t \\sin^{3}\omega t=\frac{1}{4}\left ( 3sin\omega t - sin3\omega t \right )\\$

The two functions individually represent SHM but their superposition does not give rise to SHM but the motion will definitely be periodic with a period of $\frac{2\pi }{\omega }$

Q. 14.4 (c) Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion ( $\omega$ is any positive constant):

Answer:

The function represents SHM with a period of $\frac{\pi }{\omega }$

Q. 14.4 (c)Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion ( is any positive constant): (c)

Q.14.4 (d) Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):

(d) $cos\; \omega t+cos\; 3\omega t+cos\; 5\omega t$

Answer:

Here each individual functions are SHM. But superposition is not SHM. The function represents periodic motion but not SHM.

$period=LCM(\frac{2\pi}{\omega},\frac{2\pi}{3\omega},\frac{2\pi}{5\omega})=\frac{2\pi}{\omega}$

Q. 14.4 (e) Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):

(e) $exp(-\omega ^{2}t^{2})$

Answer:

The given function is exponential and therefore does not represent periodic motion.

Q. 14.4 (f) Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):

(f) $1+\omega t+\omega^{2}t^{2}$

Answer:

The given function does not represent periodic motion.

Q. 14.5 (a) A particle is in linear simple harmonic motion between two points, A and B, $10cm$ apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is

(a) at the end A,

Answer:

Velocity is zero. Force and acceleration are in the positive direction.

Q. 14.5 (b) A particle is in linear simple harmonic motion between two points, $A$ and $B$ , $10cm$ apart. Take the direction from A to $B$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is

(b) at the end $B$ ,

Answer:

Velocity is zero. Acceleration and force are negative.

Q. 14.5 (c) A particle is in linear simple harmonic motion between two points, $A$ and $B$ , $10 \; cm$ apart. Take the direction from $A$ to $B$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is

Answer:

Velocity is negative that is towards A and its magnitude is maximum. Acceleration and force are zero.

Q. 14.5 (d) A particle is in linear simple harmonic motion between two points, $A$ and $B$ , $10cm$ apart. Take the direction from $A$ to $B$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is

(d) at $2cm$ away from $B$ going towards $A$ ,

Answer:

Velocity is negative. Acceleration and force are also negative.

Q.14.5 (e) A particle is in linear simple harmonic motion between two points, $A$ and $B$ , $10cm$ apart. Take the direction from $A$ to $B$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is

(e) at $3cm$ away from $A$ going towards $B$ , and

Answer:

Velocity is positive. Acceleration and force are also positive.

Q. 14.5 (f) A particle is in linear simple harmonic motion between two points, $A$ and $B$ , $10cm$ apart. Take the direction from $A$ to $B$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is

(f) at $4cm$ away from $B$ going towards $A.$

Answer:

Velocity, acceleration and force all are negative

Q. 14.6 Which of the following relationships between the acceleration a and the displacement $x$ of a particle involve simple harmonic motion?

(a) $a=0.7x$

(b) $a=-200x^2$

(d) $a=100x^3$

Answer:

Only the relation given in (c) represents simple harmonic motion as the acceleration is proportional in magnitude to the displacement from the midpoint and its direction is opposite to that of the displacement from the mean position.

Q. 14.7 The motion of a particle executing simple harmonic motion is described by the displacement function, $x(t)=A \; cos(\omega t+\phi ).$

If the initial $(t=0)$ position of the particle is $1\; cm$ and its initial velocity is $\omega \; cm/s,$ what are its amplitude and initial phase angle ? The angular frequency of the particle is $\pi s^{-1}.$ If instead of the cosine function, we choose the sine function to describe the SHM : $x=B\; sin(\omega t+\alpha ),$ what are the amplitude and initial phase of the particle with the above initial conditions.

Answer:

$\omega =\pi\ rad\ s^{-1}$

$x(t)=Acos(\pi t+\phi )$

at t = 0

$\\x(0)=Acos(\pi \times 0+\phi )\\ 1=Acos\phi\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (i)$

$\\v=\frac{\mathrm{d}x(t) }{\mathrm{d} t}\\ v(t)=-A\pi sin(\pi t+ \phi )$

at t = 0

$\\v(0) =-A\pi sin(\pi \times 0+ \phi ) \\ \omega =-A\pi sin\phi\\\ 1 =-A sin\phi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (ii)$

Squaring and adding equation (i) and (ii) we get

$\\1^{2}+1^{2}=(Acos\phi )^{2}+(-Asin\phi )^{2} \\2=A^{2}cos^{2}\phi +A^{2}sin^{2}\phi \\ 2=A^{2}\\ A=\sqrt{2}$

Dividing equation (ii) by (i) we get

$\\tan\phi =-1\\ \phi =\frac{3\pi }{4},\frac{7\pi }{4},\frac{11\pi }{4}......$

$x(t)=Bsin(\pi t+\alpha )$

at t = 0

$\\x(0)=Bsin(\pi \times 0+\alpha )\\ 1=Bsin\alpha \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (iii)$

$\\v=\frac{\mathrm{d}x(t) }{\mathrm{d} t}\\ v(t)=B\pi cos(\pi t+ \alpha )$

at t = 0

$\\v(0) =B\pi cos(\pi \times 0+ \alpha ) \\ \omega =B\pi cos\alpha \\\ 1 =B cos\alpha \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (iv)$

Squaring and adding equation (iii) and (iv) we get

$\\1^{2}+1^{2}=(Bsin\alpha )^{2}+(Bcos\alpha )^{2} \\2=B^{2}sin^{2}\alpha +B^{2}cos^{2}\alpha \\ 2=B^{2}\\ B=\sqrt{2}$

Dividing equation (iii) by (iv) we get

$\\tan\alpha =1\\ \alpha =\frac{\pi }{4},\frac{5\pi }{4},\frac{9\pi }{4}......$

Q. 14.8 A spring balance has a scale that reads from $0$ to $50\; kg.$ The length of the scale is $20 cm,$ A body suspended from this balance, when displaced and released, oscillates with a period of $0.6\; s.$ What is the weight of the body?

Answer:

Spring constant of the spring is given by

$\\k=\frac{Weight\ of\ Maximum\ mass\ the\ scale\ can\ read}{Maximum\ displacement\ of\ the\ scale}\\ k=\frac{50\times 9.8}{20\times 10^{-2}}\\ k=2450\ Nm^{-1}$

The time period of a spring attached to a body of mass m is given by

$\\T=2\pi \sqrt{\frac{m}{k}}\\ m=\frac{T^{2}k}{4\pi ^{2}}\\ m=\frac{(0.6)^{2}\times 2450}{4\pi ^{2}}\\ m=22.34\ kg\\ w=mg\\ w=22.34\times 9.8\\ w=218.95\ N$

Q. 14.9 (i) A spring having with a spring constant $1200\; N\; m^{-1}$ is mounted on a horizontal table as shown in Fig. 14.24. A mass of $3\; kg$ is attached to the free end of the spring. The mass is then pulled sideways to a distance of $2.0\; cm$ and released.

Determine

(i) the frequency of oscillations,

Answer:

The frequency of oscillation of an object of mass m attached to a spring of spring constant k is given by

$\\\nu =\frac{1}{2\pi }\sqrt{\frac{k}{m}}\\ \nu =\frac{1}{2\pi }\times \sqrt{\frac{1200}{3}}\\ \nu =3.183\ Hz$

Q. 14.9 (ii) A spring having with a spring constant $1200\; N\; m^{-1}$ is mounted on a horizontal table as shown in Fig. 14.24. A mass of $3\; kg$ is attached to the free end of the spring. The mass is then pulled sideways to a distance of $2.0\; cm$ and released.

Determine

(ii) maximum acceleration of the mass, and

Answer:

A body executing S.H.M experiences maximum acceleration at the extreme points

$\\a_{max}=\frac{F_{A}}{m}\\ a_{max}=\frac{kA}{m}\\ a_{max}=\frac{1200\times 0.2}{3} \\a_{max}=8ms^{-2}$ (F _A = Force experienced by body at displacement A from mean position)

Q. 14.9 (iii) A spring having with a spring constant $1200\; N\; m^{-1}$ is mounted on a horizontal table as shown in Fig. 14.24. A mass of $3\; kg$ is attached to the free end of the spring. The mass is then pulled sideways to a distance of $2.0 \; cm$ and released.

Determine

(iii) the maximum speed of the mass.

Answer:

Maximum speed occurs at the mean position and is given by

$\\v_{max}=A\omega \\ v_{max}=0.02\times 2\pi \times 3.18\\ v_{max}=0.4ms^{-1}$

Q. 14.10 (a) In Exercise 14.9, let us take the position of mass when the spring is unstreched as $x=0,$ and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch $(t=0),$ the mass is

(a) at the mean position,

In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?

Answer:

Amplitude is A = 0.02 m

Time period is $\\\omega$

$\\\omega =\sqrt{\frac{k}{m}}\\ \omega =\sqrt{\frac{1200}{3}}\\ \omega =20\ rad/s$

(a) At t = 0 the mass is at mean position i.e. at t = 0, x = 0

$\\x(t)=0.02sin\left ( 20t \right )$

Here x is in metres and t is in seconds.

Q. 14.10 (b) In Exercise 14.9, let us take the position of mass when the spring is unstreched as $x=0,$ and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch $(t=0),$ the mass is

(b) at the maximum stretched position,

In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?

Answer:

Amplitude is A = 0.02 m

Time period is $\\\omega$

$\\\omega =\sqrt{\frac{k}{m}}\\ \omega =\sqrt{\frac{1200}{3}}\\ \omega =20\ rad/s$

(b) At t = 0 the mass is at the maximum stretched position.

x(0) = A

$\phi =\frac{\pi }{2}$

$\\x(t)=0.02sin\left ( 20t + \frac{\pi }{2}\right )\\ x(t)=0.02cos(20t)$

Here x is in metres and t is in seconds.

Q. 14.10 (c) In Exercise 14.9, let us take the position of mass when the spring is unstreched as $x=0,$ and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch $(t=0),$ the mass is

In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?

Answer:

Amplitude is A = 0.02 m

Time period is $\\\omega$

$\\\omega =\sqrt{\frac{k}{m}}\\ \omega =\sqrt{\frac{1200}{3}}\\ \omega =20\ rad/s$

x(0) = -A

$\phi =\frac{3\pi }{2}$

$\\x(t)=0.02sin\left ( 20t + \frac{3\pi }{2}\right )\\ x(t)=-0.02cos(20t)$

Here x is in metres and t is in seconds.

The above functions differ only in the initial phase and not in amplitude or frequency.

Q. 14.11 Figures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

1650450107919

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.

Answer:

(a) Let the required function be $x(t)=asin(\pm \omega t+\phi )$

Amplitude = 3 cm = 0.03 m

T = 2 s

$\\\omega =\frac{2\pi }{T}\\ \omega =\pi rad\ s$

Since initial position x(t) = 0, $\phi =0$

As the sense of revolution is clock wise

$\\x(t)=0.03sin(-\omega t)\\ x(t)=-0.03sin(\pi t)$

Here x is in metres and t is in seconds.

(b)Let the required function be $x(t)=asin(\pm \omega t+\phi )$

Amplitude = 2 m

T = 4 s

$\\\omega =\frac{2\pi }{T}\\ \omega =\frac{\pi }{2} rad\ s$

Since initial position x(t) = -A, $\phi =\frac{3\pi }{2}$

As the sense of revolution is anti-clock wise

$\\x(t)=2sin(\omega t+\frac{3\pi }{2})\\ x(t)=-2cos(\frac{\pi }{2} t)$

Here x is in metres and t is in seconds.

Q. 14.12 (a) Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial $(t=0)$ position of the particle, the radius of the circle and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).

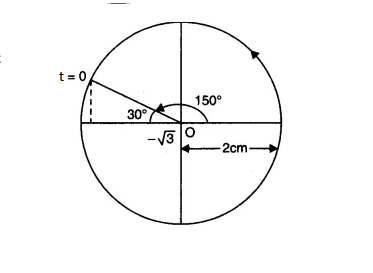
(a) $x=-2\; sin(3t+\pi /3)$

Answer:

$\\x=-2\sin(3t+\pi /3)\\ x=2cos(3t+\frac{\pi }{3}+\frac{\pi }{2})\\ x=2cos(3t+\frac{5\pi }{6})$

The initial position of the particle is x(0)

$\\x(0)=2cos(0+\frac{5\pi }{6})\\ x(0)=2cos(\frac{5\pi }{6})\\ x(0)=-\sqrt{3}cm$

The radius of the circle i.e. the amplitude is 2 cm

The angular speed of the rotating particle is $\omega =3rad\ s^{-1}$

Initial phase is

$\\\phi =\frac{5\pi }{6}\\ \phi =150^{o}$

The reference circle for the given simple Harmonic motion is

1650450164265

Q. 14.12 (b) Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial $(t=0)$ position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).

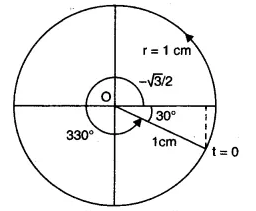
(b) $x=cos(\pi /6-t)$

Answer:

$\\x(t)=cos(\frac{\pi }{6}-t)\\ x(t)=cos(t-\frac{\pi }{6})$

The initial position of the particle is x(0)

$\\x(0)=cos(0-\frac{\pi }{6})\\ x(0)=cos(\frac{\pi }{6})\\ x(0)=\frac{\sqrt{3}}{2}cm$

The radius of the circle i.e. the amplitude is 1 cm

The angular speed of the rotating particle is $\omega =1rad\ s^{-1}$

Initial phase is

$\\\phi =-\frac{\pi }{6}\\ \phi =-30^{o}$

The reference circle for the given simple Harmonic motion is

1650450237789

Q. 14.12 (c) Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial $(t=0)$ position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).

Answer:

$x=3\; sin(2\pi t+\pi /4)$

$\\x=-3cos(2\pi t+\frac{\pi}{4}+\frac{\pi}{2})\\ \ =3cos(2\pi t+\pi+\frac{\pi}{4}+\frac{\pi}{2})\\=3cos(2\pi t+\frac{3\pi}{2}+\frac{\pi}{4})\\=3cos(2\pi t+\frac{7\pi}{4})$

At t= 0

$phase=\frac{7\pi}{4}$

Reference circle is as follows

osccc12c

Oscillations Excercise:

Question:

Q. 14.12 (d) Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial $(t=0)$ position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).

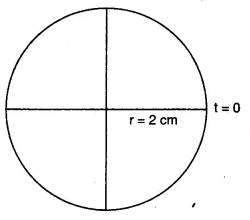
(d) $x=2\; cos\; \pi t$

Answer:

$\\x(t)=2cos(\pi t)\\$

The initial position of the particle is x(0)

$\\x(0)=2cos(0)\\ x(0)=2cm$

The radius of the circle i.e. the amplitude is 2 cm

The angular speed of the rotating particle is $\omega =\pi rad\ s^{-1}$

Initial phase is

$\\\phi =0^{o}$

The reference circle for the given simple Harmonic motion is

1650450280990

Q. 14.13 (a) Figure 14.30

(a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. $A$ force $F$ applied at the free end stretches the spring. Figure 14.30 (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Fig. 14.30

(b) is stretched by the same force F.

1650450344807

(a) What is the maximum extension of the spring in the two cases?

Answer:

(a) Let us assume the maximum extension produced in the spring is x.

At maximum extension

$\\F=Kx\\ x=\frac{F}{k}$

(b) Let us assume the maximum extension produced in the spring is x. That is x/2 due to force towards left and x/2 due to force towards right

$\\F=k\frac{x}{2}+k\frac{x}{2}\\\Rightarrow x=\frac{F}{k}$

Oscillations Excercise:

Question:

Q. 14.13 (b) Figure 14.26 (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. $A$ force $F$ applied at the free end stretches the spring. Figure 14.26 (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Fig. 14.26 (b) is stretched by the same force $F$ .

1650450400570

(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the period of oscillation in each case?

Answer:

(b).(a) In Fig, (a) we have

F=-kx

ma=-kx

$a=-\frac{k}{m}x$

$\\\omega ^{2}=\frac{k}{m}\\ T=\frac{2\pi }{\omega }\\ T=2\pi \sqrt{\frac{m}{k}}$

(b) In fig (b) the two equal masses will be executing SHM about their centre of mass. The time period of the system would be equal to a single object of same mass m attached to a spring of half the length of the given spring (or undergoing half the extension of the given spring while applied with the same force)

Spring constant of such a spring would be 2k

F=-2kx

ma=-2kx

$\\a=-\frac{2k}{m}x\\ \omega ^{2}=\frac{2k}{m}\\ T=\frac{2\pi }{\omega }\\ T=2\pi \sqrt{\frac{m}{2k}}\\ T=\pi \sqrt{\frac{2m}{k}}$

Q. 14.14 The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of $1.0 m$ If the piston moves with simple harmonic motion with an angular frequency of $200\; rad/min,$ what is its maximum speed ?

Answer:

Amplitude of SHM = 0.5 m

angular frequency is

$\\\omega =200\ rad/min \\\omega =3.33\ rad/s$

If the equation of SHM is given by

$\\x(t)=Asin(\omega t+\phi )\\$

The velocity would be given by

$\\v(t)=\frac{\mathrm{d} x(t)}{\mathrm{d} t}\\ v(t)=\frac{\mathrm{d} (Asin(\omega t+\phi ))}{\mathrm{d} t}\\ v(t)=A\omega cos(\omega t+\phi )$

The maximum speed is therefore

$\\v_{max}=A\omega \\ v_{max}=0.5\times 3.33 \\v_{max}=1.67ms^{-1}$

Q. 14.15 The acceleration due to gravity on the surface of moon is $1.7m\; s^{-2}$ What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is $3.5\; s$ ? (g on the surface of earth is 9.8 m s–2)

Answer:

The time period of a simple pendulum of length l executing S.H.M is given by

$T=2\pi \sqrt{\frac{l}{g}}$

g _e = 9.8 m s ^-2

g _m = 1.7 m s ^-2

The time period of the pendulum on the surface of Earth is T _e = 3.5 s

The time period of the pendulum on the surface of the moon is T _m

$\\\frac{T_{m}}{T_{e}}=\sqrt{\frac{g_{e}}{g_{m}}}\\ T_{m}=T_{e}\times \sqrt{\frac{g_{e}}{g_{m}}}\\ T_{m}=3.5\times \sqrt{\frac{9.8}{1.7}} \\T_{m}=8.4s$

Q. 14.16 (a) Answer the following questions :

(a) Time period of a particle in SHM depends on the force constant k and mass m of the particle:

$T=2\pi \sqrt{\frac{m}{k}}.$ A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum?

Answer:

In case of spring, the spring constant is independent of the mass attached whereas in case of a pendulum k is proportional to m making k/m constant and thus the time period comes out to be independent of the mass of the body attached.

Q. 14.16 (b) Answer the following questions :

(b) The motion of a simple pendulum is approximately simple harmonic for small angle oscillations: For larger angles of oscillation, a more involved analysis shows that T is greater than $2\pi \sqrt{\frac{l}{g}}.$ Think of a qualitative argument to appreciate this result.

Answer:

In reaching the result $T=2\pi \sqrt{\frac{l}{g}}$ we have assumed sin(x/l)=x/l. This assumption is only true for very small values of x $(or\ \theta )$ . Therefore it is obvious that once x takes larger values we will have deviations from the above-mentioned value.

Q. 14.16 (c) Answer the following questions :

(c) A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?

Answer:

The watch must be using an electrical circuit or a spring system to tell the time and therefore free falling would not affect the time his watch predicts.

Q. 14.16 (d) Answer the following questions :

(d) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?

Answer:

While free falling the effective value of g inside the cabin will be zero and therefore the frequency of oscillation of a simple pendulum would be zero i.e. it would not vibrate at all because of the absence of a restoring force.

Q .14.17 A simple pendulum of length l and having a bob of mass $M$ is suspended in a car.The car is moving on a circular track of radius $R$ with a uniform speed $V$ . If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?

Answer:

Acceleration due to gravity = g (in downwards direction)

Centripetal acceleration due to the circular movement of the car = a _c

$a_{c}=\frac{v^{2}}{R}$ (in the horizontal direction)

Effective acceleration is

$\\g'=\sqrt{g^{2}+a_{c}^{2}}\\ g'=\sqrt{g^{2}+\frac{v^{4}}{R^{2}}}$

The time period is T'

$\\T'=2\pi \sqrt{\frac{l}{g'}}\\ T'=2\pi \sqrt{\frac{l}{\sqrt{g^{2}+\frac{v^{4}}{R^{2}}}}}$

Q. 14.18 A cylindrical piece of cork of density of base area A and height h floats in a liquid of density $\rho _{\imath }$ . The cork is depressed slightly and then released

Show that the cork oscillates up and down simple harmonically with a period $T=2\pi \sqrt{\frac{h\rho }{\rho _{ 1}g}}$ where $\rho$ is the density of cork. (Ignore damping due to viscosity of the liquid).

Answer:

Let the cork be displaced by a small distance x in downwards direction from its equilibrium position where it is floating.

The extra volume of fluid displaced by the cork is Ax

Taking the downwards direction as positive we have

$\\ma=-\rho _{1}gAx\\ \rho Aha=-\rho _{1}gAx\\ \frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}=-\frac{\rho _{1}g}{\rho h}x$

Comparing with a=-kx we have

$\\k=\frac{\rho _{1}g}{\rho h}\\ T=\frac{2\pi }{\sqrt{k}}\\ T=2\pi \sqrt{\frac{\rho h}{\rho_{1}g }}$

Q. 14.19 One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.

Answer:

Let the height of each mercury column be h.

The total length of mercury in both the columns = 2h.

Let the cross-sectional area of the mercury column be A.

Let the density of mercury be $\rho$

When either of the mercury columns dips by a distance x, the total difference between the two columns becomes 2x.

Weight of this difference is $2Ax\rho g$

This weight drives the rest of the entire column to the original mean position.

Let the acceleration of the column be a Since the force is restoring

$\\2hA\rho (-a)=2xA\rho g\\ a=-\frac{g}{h}x$

$\frac{\mathrm{d}^{2}x }{\mathrm{d} t^{2}}=-\frac{g}{h}x$ which is the equation of a body executing S.H.M

The time period of the oscillation would be

$T=2\pi \sqrt{\frac{h}{g}}$

NCERT solutions for class 11 physics chapter 14 oscillations: Additional Exercise Solution

Q. 14.20 An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.33). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.33].

1650450479295

Answer:

Let the initial volume and pressure of the chamber be V and P.

Let the ball be pressed by a distance x.

This will change the volume by an amount ax.

Let the change in pressure be $\Delta P$

Let the Bulk's modulus of air be K.

$\\K=\frac{\Delta P}{\Delta V/V}\\ \Delta P=\frac{Kax}{V}$

This pressure variation would try to restore the position of the ball.

Since force is restoring in nature displacement and acceleration due to the force would be in different directions.

$\\F=a\Delta P\\ -m\frac{\mathrm{d^{2}}x }{\mathrm{d}t^{2}}=a\Delta p\\ \frac{\mathrm{d^{2}}x }{\mathrm{d}t^{2}}=-\frac{ka^{2}}{mV}x$

The above is the equation of a body executing S.H.M.

The time period of the oscillation would be

$T=\frac{2\pi }{a}\sqrt{\frac{mV}{k}}$

Q. 14.21 (a) You are riding in an automobile of mass $3000\; kg.$ . Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags $15\; cm$ when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by $50^{o}/_{o}$ during one complete oscillation. Estimate the values of

(a) the spring constant $K$

Answer:

Mass of automobile (m) = 3000 kg

There are a total of four springs.

Compression in each spring, x = 15 cm = 0.15 m

Let the spring constant of each spring be k

$\\4kx=mg\\ k=\frac{3000\times 9.8}{4\times 0.15}\\ k=4.9\times 10^{4}\ N$

Q. 14.21 (b) You are riding in an automobile of mass $3000kg\;$ . Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags $15\; cm$ when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by $50^{o}/_{o}$ during one complete oscillation. Estimate the values of

(b) the damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports $750 \; kg.$ .

Answer:

The amplitude of oscillation decreases by 50 % in one oscillation i.e. in one time period.

$\\T=2\pi \sqrt{\frac{m}{k}}\\ T=2\pi \times \sqrt{\frac{3000}{4\times 4.9\times 10^{4}}}\\ T=0.77\ s$

For damping factor b we have

$x=x_{0}e^{\left ( -\frac{bt}{2m} \right )}$

x=x ₀ /2

t=0.77s

m=750 kg

$\\e^{-\frac{0.77b}{2\times 750}}=0.5\\ ln(e^{-\frac{0.77b}{2\times 750}})=ln0.5\\ \frac{0.77b}{1500}=ln2\\ b=\frac{0.693\times 1500}{0.77}\\ b=1350.2287\ kg\ s^{-1}$

14.22 Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.

Answer:

Let the equation of oscillation be given by $x=Asin(\omega t)$

Velocity would be given as

$\\v=\frac{dx}{dt}\\ v=A\omega cost(\omega t)$

Kinetic energy at an instant is given by

$\\K(t)=\frac{1}{2}m(v(t))^{2}\\ K(t)=\frac{1}{2}m(A\omega cos(\omega t))^{2}\\ K(t)=\frac{1}{2}mA^{2}\omega ^{2}cos^{2}\omega t$

Time Period is given by

$T=\frac{2\pi }{\omega }$

The Average Kinetic Energy would be given as follows

$\\K_{av}=\frac{\int _{0}^{T}K(t)dt}{\int _{0}^{T}dt}\\ K_{av}=\frac{1}{T}\int _{0}^{T}K(t)dt\\ K_{av}=\frac{1}{T}\int_{0}^{T}\frac{1}{2}mA^{2}\omega ^{2}cos^{2}\omega t\ dt\\K_{av}=\frac{mA^{2}\omega ^{2}}{2T}\int_{0}^{T}cos^{2}\omega t\ dt\\ K_{av}=\frac{mA^{2}\omega ^{2}}{2T}\int_{0}^{T}\left ( \frac{1+cos2\omega t}{2} \right )dt$

$\\K_{av}=\frac{mA^{2}\omega ^{2}}{2T}\left [ \frac{t}{2} +\frac{sin2\omega t}{4\omega }\right ]_{0}^{T}\\ K_{av}=\frac{mA^{2}\omega ^{2}}{2T}\left [ \left ( \frac{T}{2}+\frac{sin2\omega T}{4\omega } \right )-\left ( 0+sin(0) \right ) \right ]\\ K_{av}=\frac{mA^{2}\omega ^{2}}{2T}\times \frac{T}{2}\\ K_{av}=\frac{mA^{2}\omega ^{2}}{4}$

The potential energy at an instant T is given by

$\\U(t)=\frac{1}{2}kx^{2}\\ U(t)=\frac{1}{2}m\omega ^{2}(Asin(\omega t))^{2}\\ U(t)=\frac{1}{2}m\omega ^{2}A^{2}sin^{2}\omega t$

The Average Potential Energy would be given by

$\\U_{av}=\frac{\int_{0}^{T}U(t)dt}{\int_{0}^{T}dt}\\ \\U_{av}=\frac{1}{T}\int_{0}^{T}\frac{1}{2}m\omega ^{2}A^{2}sin^{2}\omega t\ dt\\ \\U_{av}=\frac{m\omega ^{2}A^{2}}{2T}\int_{0}^{T}sin^{2}\omega t\ dt\\\\ \\U_{av}=\frac{m\omega ^{2}A^{2}}{2T}\int_{0}^{T}\frac{(1-cos2\omega t)}{2}dt$

$\\U_{av}=\frac{m\omega ^{2}A^{2}}{2T}\left [ \frac{t}{2} -\frac{sin2\omega t}{4\omega }\right ]_{0}^{T}\\ \\U_{av}=\frac{m\omega ^{2}A^{2}}{2T}\left [ \left ( \frac{T}{2}-\frac{sin2\omega T}{4\omega } \right )-\left ( 0-sin0 \right ) \right ]\\ U_{av}=\frac{m\omega ^{2}A^{2}}{2T}\times \frac{T}{2}\\ U_{av}=\frac{m\omega ^{2}A^{2}}{4}$

We can see K _av = U _av

Q .14.23 A circular disc of mass $10\; kg$ is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be $1.5 \; s.$ The radius of the disc is $15 \; cm$ . Determine the torsional spring constant of the wire. (Torsional spring constant $a$ is defined by the relation $J=-a\; \theta$ , where J is the restoring couple and θ the angle of twist).

Answer:

$J=-a\; \theta$

Moment of Inertia of the disc about the axis passing through its centre and perpendicular to it is

$I=\frac{MR^{2}}{2}$

$\\J=I\frac{\mathrm{d}^{2}\theta }{\mathrm{d} t^{2}}\\ -a\theta =\frac{MR^{2}}{2}\frac{\mathrm{d}^{2}\theta }{\mathrm{d} t^{2}}\\ \frac{\mathrm{d}^{2}\theta }{\mathrm{d} t^{2}}=-\frac{2a}{MR^{2}}\theta$

The period of Torsional oscillations would be

$\\T=2\pi \sqrt{\frac{MR^{2}}{2a}}\\ a=\frac{2\pi ^{2}MR^{2}}{T^{2}}\\ a=\frac{2\pi ^{2}\times 10\times (0.15)^{2}}{(1.5)^{2}}\\ a=1.97\ N\ m\ rad^{-1}$

Q. 14.24 (a) A body describes simple harmonic motion with an amplitude of $5\; cm$ and a period of $0.2\; s.$ Find the acceleration and velocity of the body when the displacement is

(a) $5\; cm$

Answer:

A = 5 cm = 0.05 m

T = 0.2 s

$\\\omega =\frac{2\pi }{T}\\ \omega =\frac{2\pi }{0.2}\\ \omega =10\pi\ rad\ s^{-1}$

At displacement x acceleration is $a=-\omega ^{2}x$

At displacement x velocity is $v=\omega \sqrt{A^{2}-x^{2}}$

(a)At displacement 5 cm

$\\v=10\pi \sqrt{(0.05)^{2}-(0.05)^{2}}\\ v=0$

$\\a=-(10\pi )^{2}\times 0.05\\a=-49.35ms^{-2}$

Q. 14.24 (b) A body describes simple harmonic motion with an amplitude of $5\; cm$ and a period of $0.2 \; s.$ Find the acceleration and velocity of the body when the displacement is

(b) $3\; cm$

Answer:

A = 5 cm = 0.05 m

T = 0.2 s

$\\\omega =\frac{2\pi }{T}\\ \omega =\frac{2\pi }{0.2}\\ \omega =10\pi\ rad\ s^{-1}$

At displacement x acceleration is $a=-\omega ^{2}x$

At displacement x velocity is $v=\omega \sqrt{A^{2}-x^{2}}$

(a)At displacement 3 cm

$\\v=10\pi \sqrt{(0.05)^{2}-(0.03)^{2}}\\ v=10\pi \sqrt{0.0016}\\v=10\pi \times 0.04\\v=1.257ms^{-1}$

$\\a=-(10\pi )^{2}\times 0.03\\a=-29.61ms^{-2}$

Q. 14.24 (c) A body describes simple harmonic motion with an amplitude of $5\; cm$ and a period of $0.2\; s.$ Find the acceleration and velocity of the body when the displacement is

Answer:

A = 5 cm = 0.05 m

T = 0.2 s

$\\\omega =\frac{2\pi }{T}\\ \omega =\frac{2\pi }{0.2}\\ \omega =10\pi\ rad\ s^{-1}$

At displacement x acceleration is $a=-\omega ^{2}x$

At displacement x velocity is $v=\omega \sqrt{A^{2}-x^{2}}$

(a)At displacement 0 cm

$\\v=10\pi \sqrt{(0.05)^{2}-(0)^{2}}\\ v=10\pi \times 0.05\\v=1.57ms^{-1}$

$\\a=-(10\pi )^{2}\times0\\a=0$

Q. 14.25 A mass attached to a spring is free to oscillate, with angular velocity $\omega$ , in a horizontal plane without friction or damping. It is pulled to distance $x_{0}$ and pushed towards the centre with a velocity $v_{0}$ at time $t=0$ Determine the amplitude of the resulting oscillations in terms of the parameters $\omega$ , $x_{0}$ and $v_{0}$ . [Hint : Start with the equation $x=a\; cos(\omega t+\theta )$ and note that the initial velocity is negative.]

Answer:

At the maximum extension of spring, the entire energy of the system would be stored as the potential energy of the spring.

Let the amplitude be A

$\\\frac{1}{2}kA^{2}=\frac{1}{2}mv_{0}^{2}+\frac{1}{2}kx_{0}^{2}\\ A=\sqrt{x_{0}^{2}+\frac{m}{k}v_{0}^{2}}$

The angular frequency of a spring-mass system is always equal to $\sqrt{\frac{k}{m}}$

Therefore

$A=\sqrt{x_{0}^{2}+\frac{v_{0}^{2}}{\omega ^{2}}}$

oscillation class 11 physics

oscillations class 11 ncert solutions cover the theory and applications of the concept that any material medium can be represented as a collection of many interconnected oscillators, forming a medium of waves. The chapter explains this concept in detail.

When using the oscillations ncert solutions, students will gain an understanding of the various factors that impact the movement of an object. These factors include period, frequency, harmonic motion, and uniform circular motion.class 11 physics chapter 14 ncert solutions offers a comprehensive study of these important topics, including details such as systems that execute harmonic motion, like springs, forced oscillations, force laws, velocity, and more. The solutions have been prepared with careful attention to even the smallest details, in order to provide students with a thorough understanding of the subject matter.

NCERT solutions for class 11 physics chapter-wise

Chapter 1	Physical world
Chapter 2	Units and Measurement
Chapter 3	Motion in a straight line
Chapter 4	Motion in a Plane
Chapter 5	Laws of Motion
Chapter 6	Work, Energy and Power
Chapter 7	System of Particles and Rotational motion
Chapter 8	Gravitation
Chapter 9	Mechanical Properties of Solids
Chapter 10	Mechanical Properties of Fluids
Chapter 11	Thermal Properties of Matter
Chapter 12	Thermodynamics
Chapter 13	Kinetic Theory
Chapter 14	Oscillations
Chapter 15	Waves

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Oscillations Class 11 NCERT Topics

14.1 Introduction

14.2 Periodic and oscillatory motions

14.3 Simple harmonic motion

14.4 Simple harmonic motion and uniform circular motion

14.5 Velocity and acceleration in simple harmonic motion

14.6 Force law for simple harmonic motion

14.7 Energy in simple harmonic motion

14.8 Some systems executing simple harmonic motion

14.9 Damped simple harmonic motion

14.10 Forced oscillations and resonance

Other types of oscillatory motions that are discussed in the Oscillations Class 11 Chapter 14 are damped oscillations and forced oscillations. In damped oscillation, as the name indicates the oscillation gets damped after an interval of time.

We have seen the oscillation of a pendulum, this oscillation will be damped unless an external force is applied to maintain the oscillation. Such maintained oscillation due to an external agency is called forced or driven oscillations.

Importance of NCERT Solutions for Class 11 Physics Chapter 14 Oscillations:

On an average 6.67 % of questions from oscillation and waves are asked for JEE Mains. Most of the previous JEE mains questions from oscillation asked are from topics SHM and simple pendulum. For NEET exam 2 questions are expected from oscillation. The CBSE NCERT solutions for Class 11 Physics chapter 14 Oscillations will help to score well in Class 11 and competitive exams.

Key features of NCERT Solutions for Class 11 Physics Chapter 14

Comprehensive Coverage: These ch 14 physics class 11 ncert solutions cover all the important topics and questions presented in the chapter, ensuring a thorough understanding of oscillatory motion.
Exercise and Additional Exercise Solutions: Detailed solutions for oscillation exercise class 12 questions (14.1 to 14.19) and additional exercise questions (14.20 to 14.25) are provided, facilitating practice and self-assessment.
Clarity and Simplicity: The oscillation chapter class 11 solutions are explained in clear and simple language, making complex concepts more accessible to students.
Problem-Solving Skills: By practising with these solutions, students develop strong problem-solving skills, which are essential in physics and other subjects.
Exam Preparation: These solutions are designed to help students prepare effectively for their exams, including board exams and competitive exams like JEE and NEET.

NCERT solutions for class 11 Subject wise

NCERT solutions for Class 11 Biology

NCERT solutions for Class 11 Maths

NCERT solutions for Class 11 Chemistry

Also Check NCERT Books and NCERT Syllabus here

Subject wise NCERT Exemplar solutions

Frequently Asked Question (FAQs)

1. What is the weightage of Oscillations Class 11 for NEET

From the NCERT chapter oscillations, two questions can be expected for NEET exam. For more questions solve NEET previous year papers.

2. Is the chapter oscillation important for JEE Main

Yes, oscillation is important for JEE Main. One or two question can be expected from oscillations for JEE Main. It is one of the important chapter for scholarship exams like KVPY and NSEP. To solve more problems on Oscillations refer to NCERT book, NCERT exemplar and JEE main previous year papers.

3. What is SHM in ch 14 physics class 11?

In Chapter 14 of Physics Class 11, SHM refers to Simple Harmonic Motion, which is a type of periodic motion where an object oscillates back and forth around an equilibrium point, following a sinusoidal or circular path.

4. What is the Doppler effect?

The Doppler effect is a change in the frequency of a wave perceived by an observer due to relative motion between the wave source and the observer. It is observed in sound and other types of waves and has important applications in various fields.

5. Where can I find precise solutions forclass 11 physics chapter 14 ncert solutions?

Careers360 provides precise oscillation questions and answers pdf , designed by Physics experts considering the new CBSE exam pattern. These solutions offer comprehensive knowledge for students to excel in their exams.

Also Read

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Class 11 Biology Chapter 19 Notes Excretory Products And Their Elimination- Download PDF Notes

NCERT Class 11 Biology Chapter 22 Notes Chemical Coordination And Integration- Download PDF Notes

Some basic concepts of Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 1 Notes - Download PDF

NCERT Class 11 Biology Chapter 21 Notes Neural Control And Coordination- Download PDF Notes

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Solutions for Miscellaneous Exercise Chapter 13 Class 11 - Limits and Derivatives

NCERT Solutions for Miscellaneous Exercise Chapter 11 Class 11 - Conic Section

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

High Salary Courses After Class 12 Science

Jul 26, 2024

Ophthalmology Courses After 12th - Eligibility, Duration, Institutes

Jul 26, 2024

BiPC Courses After 12th - Fees, Duration & Top Institutes

Jul 25, 2024

ICSO Sample Papers 2024-25 with Answers For Classes 1 to 10

Jul 25, 2024

NMMS Chhattisgarh Result 2024-25: Check Merit List, Cut Off Marks

Jul 25, 2024

UPTAC Counselling 2024 (Started): Document Verification, Date, Registration, Seat Allotment, Rules, Guidelines

Jul 25, 2024

Essay on Diwali for Students: Short Paragraph, 10 Lines on Deepavali

Jul 24, 2024

How to Study at Home? - Check 10 Tips to Study at Home

Jul 23, 2024

IIM Courses After 12th - Eligibility, Exams, Top Colleges

Jul 19, 2024

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:15 July,2024 - 14 August,2024

Eligibility Criteria

Application Process

Exam Pattern

National Institute of Open Schooling 12th Examination

Late Fee Application Date:22 July,2024 - 31 July,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Late Fee Application Date:22 July,2024 - 31 July,2024

Application Process

Exam Pattern

Mock Test

Chhattisgarh Board of Secondary Education 12th Examination

Exam Date:23 July,2024 - 12 August,2024

Exam Pattern

Admit Card

Result

Chhattisgarh Board of Secondary Education 10th Examination

Exam Date:24 July,2024 - 08 August,2024

Exam Pattern

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Top Schools

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 11 Physics Chapter 14 Oscillations

NCERT Solutions Class 11 Physics Oscillations – Download Pdf

NCERT Solutions for Class 11 Physics Chapter 14: Oscillations

NCERT Solutions For Class 11 Physics Chapter 14 Oscillations: Exercise Solution

NCERT solutions for class 11 physics chapter 14 oscillations: Additional Exercise Solution

oscillation class 11 physics

NCERT solutions for class 11 physics chapter-wise

Oscillations Class 11 NCERT Topics

Importance of NCERT Solutions for Class 11 Physics Chapter 14 Oscillations:

Key features of NCERT Solutions for Class 11 Physics Chapter 14

Also Check NCERT Books and NCERT Syllabus here

Subject wise NCERT Exemplar solutions

Frequently Asked Question (FAQs)

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

National Institute of Open Schooling 12th Examination