• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry

Edited By Saumya.Srivastava | Updated on Sep 06, 2023 07:23 PM IST | #CBSE Class 10th

Coordinate Geometry Class 10 NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry, created by experts at Careers360, provide comprehensive study material for students preparing for the CBSE Class 10 board exam. Class 10 maths ncert solutions chapter 7 cover all exercises in the NCERT textbook and are easily accessible for download. The step-by-step answers for various types of questions in the NCERT textbook can help students achieve mastery of the topics in the coordinate geometry chapter. The Class 10 maths chapter 7 NCERT solutions can be of great help for the students. If students want NCERT solutions for other classes and subjects, they can get the solutions by clicking on the above link. Students must refer to the NCERT Class 10 Maths books and read all the topics without fail.

This Story also Contains
  1. Coordinate Geometry Class 10 NCERT Solutions
  2. NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry FDF Free Download
  3. Coordinate Geometry Class 10 - Important Formulae
  4. NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry (Intext Questions and Exercise)
  5. Summary Of Class 10 maths NCERT solutions chapter 7
  6. Key Features of class 10 maths ncert solutions chapter 7
  7. NCERT Solutions for Class 10 Maths - Chapter Wise
  8. NCERT Books and NCERT Syllabus
  9. Benefits of NCERT Solutions for Class 10 maths chapter 7 Coordinate Geometry
  10. NCERT solutions of class 10 subject wise
  11. NCERT Exemplar solutions - Subject wise
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry

Also Read,

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry FDF Free Download

Download PDF

Coordinate Geometry Class 10 - Important Formulae

Distance Formulae:

  • For a line defined by two points A(x1, y1) and B(x2, y2), the distance between these points can be calculated using the formula:

  • Distance AB = √[(x2 − x1)2 + (y2 − y1)2]

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

Apply

Section Formula:

  • When a point P divides a line AB, with A(x1, y1) and B(x2, y2) as endpoints, in a ratio of m:n, the coordinates of point P can be found using the formula:

  • Point P = {(mx2 + nx1)/(m + n) ,(my2 + ny1)/(m + n)}

Midpoint Formula:

  • The midpoint of a line AB, defined by A(x1, y1) and B(x2, y2), can be determined using the following formula:

  • Midpoint P = {(x1+ x2)/2, (y1+ y2)/2}

Area of a Triangle:

  • Consider a triangle formed by points A(x1, y1), B(x2, y2), and C(x3, y3). The area of this triangle can be calculated using the formula:

Area ∆ABC = (1/2)|x1(y2 − y3) + x2(y3 – y1) + x3(y1 – y2)|

Free download NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry PDF for CBSE Exam.

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry (Intext Questions and Exercise)

Class 10 maths ch 7 solutions Exercise: 7.1

Q1 (i) Find the distance between the following pairs of points : (2, 3), (4, 1)

Answer:

Given points: (2, 3), (4, 1)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(4-2)^2+(1-3)^2} = \sqrt{4+4} = 2\sqrt{2}

Q1 (ii) Find the distance between the following pairs of points : (– 5, 7), (– 1, 3)

Answer:

Given points: (– 5, 7), (– 1, 3)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(-1+5)^2+(3-7)^2} = \sqrt{16+16} = 4\sqrt{2}

Q1 (iii) Find the distance between the following pairs of points :(a, b), (– a, – b)

Answer:

Given points: (a, b), (– a, – b)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(-a-a)^2+(-b-b)^2} = \sqrt{4(a^2+b^2)} = 2\sqrt{a^2+b^2}

Q2 Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.

Answer:

Given points: (0, 0) and (36, 15)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(36-0)^2+(15-0)^2} =\sqrt{1296+225} = \sqrt{1521} = 39

The distance between the two towns A and B is, thus 39 km for given towns location

(0,0) and (36,15) .

Q3 Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.

Answer:

Let the points (1, 5), (2, 3) and (– 2, – 11) be representing the vertices A, B, and C of the given triangle respectively.

A = (1,5),\ B = (2,3),\ C = (-2,-11)

Therefore,

AB = \sqrt{(1-2)^2+(5-3)^2} = \sqrt{5}

BC = \sqrt{(2-(-2))^2+(3-(-11))^2} = \sqrt{4^2+14^2} = \sqrt{16+196} = \sqrt{212} CA = \sqrt{(1-(-2))^2+(5-(-11))^2} = \sqrt{3^2+16^2} = \sqrt{9+256} = \sqrt{265} Since these are not satisfied.

AB+BC \neq CA

BA+AC \neq BC

BC+CA \neq BA

As these cases are not satisfied.

Hence the points are not collinear.

Q4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Answer:

The distance between two points A(x_{1},y_{1})\ and\ B(x_{2},y_{2}) is given by:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

So, we have the following points: (5, – 2), (6, 4) and (7, – 2) assuming it to be the vertices of triangle A, B, and C respectively.

AB = \sqrt{(5-6)^2+(-2-4)^2} = \sqrt{1+36} = \sqrt{37}

BC = \sqrt{(6-7)^2+(4+2)^2} = \sqrt{1+36} = \sqrt{37}

CA = \sqrt{(5-7)^2+(-2+2)^2} = \sqrt{4+0} = 2

Therefore, AB = BC

Here two sides are equal in length.

Therefore, ABC is an isosceles triangle.

Q5 In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

1638427088941

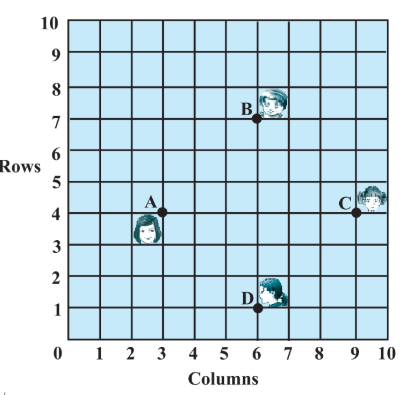
Answer:

The coordinates of the points:

A(3,4),\ B(6,7),\ C(9,4),\ and\ D(6,1) are the positions of 4 friends.

The distance between two points A(x_{1},y_{1}), \ and\ B(x_{2},y_{2}) is given by:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

Hence,

AB = \sqrt{(3-6)^2+(4-7)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

BC = \sqrt{(6-9)^2+(7-4)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

CD = \sqrt{(9-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

AD= \sqrt{(3-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

And the lengths of diagonals:

AC = \sqrt{(3-9)^2+(4-4)^2} =\sqrt{36+0} = 6

BD = \sqrt{(6-6)^2+(7-1)^2} =\sqrt{36+0} = 6

So, here it can be seen that all sides of quadrilateral ABCD are of the same lengths and diagonals are also having the same length.

Therefore, quadrilateral ABCD is a square and Champa is saying right.

Q6 (i) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)

Answer:

Let the given points (-1,-2),\ (1,0),\ (-1,2),\ and\ (-3,0) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

AB= \sqrt{(-1-1)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

BC= \sqrt{(1+1)^2+(0-2)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

CD= \sqrt{(-1+3)^2+(2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

AD= \sqrt{(-1+3)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

Finding the length of the diagonals:

AC= \sqrt{(-1+1)^2+(-2-2)^2} =\sqrt{0+16} = 4

BD= \sqrt{(1+3)^2+(0-0)^2} =\sqrt{16+0} = 4

It is clear that all sides are of the same lengths and also the diagonals have the same lengths.

Hence, the given quadrilateral is a square.

Q6 (ii) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (–3, 5), (3, 1), (0, 3), (–1, – 4)

Answer:

Let the given points (-3,5),\ (3,1),\ (0,3),\ and\ (-1,-4) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

AB= \sqrt{(-3-3)^2+(5-1)^2} =\sqrt{36+16} = \sqrt{52} = 2\sqrt{13}

BC= \sqrt{(3-0)^2+(1-3)^2} =\sqrt{9+4} = \sqrt{13}

CD= \sqrt{(0+1)^2+(3+4)^2} =\sqrt{1+49} = \sqrt{50} = 5\sqrt2

AD= \sqrt{(-3+1)^2+(5+4)^2} =\sqrt{4+81} = \sqrt{85}

All the sides of the given quadrilateral have different lengths.

Therefore, it is only a general quadrilateral and not a specific one like square, rectangle, etc.

Q6 (iii) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (4, 5), (7, 6), (4, 3), (1, 2)

Answer:

Let the given points (4,5),\ (7,6),\ (4,3),\ (1,2) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

AB= \sqrt{(4-7)^2+(5-6)^2} =\sqrt{9+1} = \sqrt{10}

BC= \sqrt{(7-4)^2+(6-3)^2} =\sqrt{9+9} = \sqrt{18}

CD= \sqrt{(4-1)^2+(3-2)^2} =\sqrt{9+1} = \sqrt{10}

AD= \sqrt{(4-1)^2+(5-2)^2} =\sqrt{9+9} = \sqrt{18}

And the diagonals:

AC =\sqrt{(4-4)^2+(5-3)^2} = \sqrt{0+4} = 2

BD =\sqrt{(7-1)^2+(6-2)^2} = \sqrt{36+16} = \sqrt{52} = 2\sqrt{13}

Here we can observe that the opposite sides of this quadrilateral are of the same length.

However, the diagonals are of different lengths.

Therefore, the given points are the vertices of a parallelogram.

Q7 Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).

Answer:

Let the point which is equidistant from A(2,-5)\ and \ B(-2,9) be X(x,0) as it lies on X-axis.

Then, we have

Distance AX: = \sqrt{(x-2)^2+(0+5)^2}

and Distance BX = \sqrt{(x+2)^2+(0+9)^2}

According to the question, these distances are equal length.

Hence we have,

\sqrt{(x-2)^2+(0+5)^2} = \sqrt{(x+2)^2+(0+9)^2}

Solving this to get the required coordinates.

Squaring both sides we get,

(x-2)^2+25 = (x+2)^2+81

\Rightarrow (x-2+x+2)(x-2-x-2)= 81 - 25 = 56

\Rightarrow (-8x)= 56

Or, \Rightarrow x = -7

Hence the point is X(-7,0) .

Q8 Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.

Answer:

Given the distance between the points P(2,-3) and Q(10,y) is 10 units.

The distance formula :

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

So, given PQ = 10\ units

PQ= \sqrt{(10-2)^2+(y-(-3))^2} = 10

After squaring both sides

\Rightarrow (10-2)^2+(y-(-3))^2 = 100

\Rightarrow (y+3)^2 = 100 - 64

\Rightarrow y+3 = \pm 6

\Rightarrow y = 6 - 3\ or\ y = -6-3

Therefore, the values are y = 3\ or -9 .

Q9 If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also, find the distances QR and PR.

Answer:

Given Q(0,1) is equidistant from P(5,-3) and R(x,6) .

Then, the distances PQ = RQ .

Distance PQ = \sqrt{(5-0)^2+(-3-1)^2} = \sqrt{25+16} = \sqrt{41}

Distance RQ = \sqrt{(x-0)^2+(6-1)^2} = \sqrt{x^2+25}

\Rightarrow \sqrt{x^2+25} = \sqrt{41}

Squaring both sides, we get

\Rightarrow x^2 = 16

\Rightarrow x = \pm 4

The points are: R(4,6)\ or\ R(-4,6.)

CASE I: when R is (4,6)

The distances QR and PR.

QR = \sqrt{(0-4)^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}

PR = \sqrt{(5-4)^2+(-3-6)^2} = \sqrt{1^2+(-9)^2} = \sqrt{1+81} = \sqrt{82}

CASE II: when R is (-4,6)

The distances QR and PR.

QR = \sqrt{(0-(-4))^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}

PR = \sqrt{(5-(-4))^2+(-3-6)^2} = \sqrt{9^2+(-9)^2} = \sqrt{81+81} = 9\sqrt{2}

Q10 Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).

Answer:

Let the point P(x,y ) is equidistant from A(3,6) and B(-3,4) .

Then, the distances AP =BP

AP = \sqrt{(x-3)^2+(y-6)^2} and BP = \sqrt{(x-(-3))^2+(y-4)^2}

\Rightarrow \sqrt{(x-3)^2+(y-6)^2} = \sqrt{(x-(-3))^2+(y-4)^2}

Squaring both sides: we obtain

\Rightarrow (x-3)^2+(y-6)^2= (x+3)^2+(y-4)^2

\Rightarrow (2x)(-6)+(2y-10)(-2)= 0 \left [\because a^2-b^2 = (a+b)(a-b) \right ]

\Rightarrow -12x-4y+20 = 0

\Rightarrow 3x+y-5 = 0

Thus, the relation is 3x+y-5 = 0 between x and y.


Class 10 maths ch 7 solutions Exercise: 7.2

Q1 Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.

Answer:

Let the coordinates of point P(x,y) which divides the line segment joining the points A(-1,7) and B(4,-3) , internally, in the ratio m_{1}:m_{2} then,

Section formula: \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Substituting the values in the formula:

Here, m_{1}:m_{2} = 2:3

\Rightarrow \left (\frac{2(4)+3(-1)}{2+3} , \frac{2(-3)+3(7)}{2+3} \right )

\Rightarrow \left (\frac{5}{5} , \frac{15}{5} \right )

Hence the coordinate is P \left (1 , 3 \right ) .

Q2 Find the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3).

Answer:

Let the trisection of the line segment A(4,-1) and B(-2,-3) have the points P(x_{1},y_{1}) and Q(x_{2},y_{2})

Then,

Section formula: \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

By observation point, P divides AB internally in the ratio 1:2 .

Hence, m:n = 1:2

Substituting the values in the equation we get;

\Rightarrow P\left (\frac{1(-2)+2(4)}{1+2} , \frac{1(-3)+2(-1)}{1+2} \right )

\Rightarrow P \left (\frac{-2+8}{3} , \frac{-3-2}{3} \right )

\Rightarrow P \left (2 , \frac{-5}{3} \right )

And by observation point Q, divides AB internally in the ratio 2:1

Hence, m:n = 2:1

Substituting the values in the equation above, we get

\Rightarrow Q\left (\frac{2(-2)+1(4)}{2+1} , \frac{2(-3)+1(-1)}{2+1} \right )

\Rightarrow Q \left (\frac{-4+4}{3} , \frac{-6-1}{3} \right )

\Rightarrow Q\left (0 , \frac{-7}{3} \right )

Hence, the points of trisections are P \left (2 , \frac{-5}{3} \right ) and Q\left (0 , \frac{-7}{3} \right )

Q3 To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. 7.12. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag

1638427152215

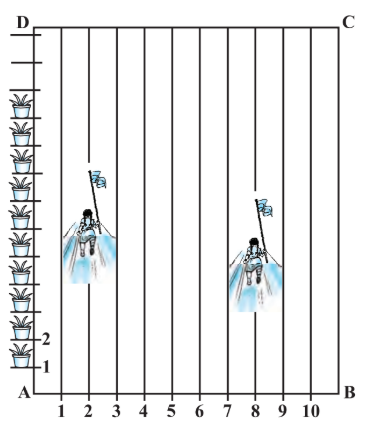
Answer:

Niharika posted the green flag at the distance P, i.e.,

\frac{1}{4}\times100\ m = 25\ m from the starting point of 2^{nd} line.

Therefore, the coordinates of this point P are (2,25).

Similarly, Preet posted red flag at \frac{1}{5} of the distance Q i.e.,

\frac{1}{5}\times100\ m = 20\ m from the starting point of 8^{th} line.

Therefore, the coordinates of this point Q are (8,20) .

The distance PQ is given by,

PQ = \sqrt{(8-2)^2+(25-20)^2} = \sqrt{36+25} = \sqrt{61} m

and the point at which Rashmi should post her Blue Flag is the mid-point of the line joining these points. Let this point be R(x,y) .

Then, by Section Formula,

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

x = \frac{2+8}{2},\ y = \frac{25+20}{2}

x = 5,\ y = 22.5

Therefore, Rashmi should post her Blue Flag at 22.5 m on the 5th line.

Q4 Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).

Answer:

Let the ratio be : k:1

Then, By section formula:

P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )

Given point P(x,y) = (-1,6)

-1 = \frac{6k-3}{k+1}

\Rightarrow -k-1 = 6k-3

\Rightarrow k = \frac{7}{2}

Hence, the point P divides the line AB in the ratio 2:7 .

Q5 Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.

Answer:

Let the point on the x-axis be P(x,0) and it divides it in the ratio k:1 .

Then, we have

Section formula:

P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )

\implies \frac{ky_{2}+y_{1}}{k+1} = 0

k =-\frac{y_{1}}{y_{2}}

Hence, the value of k will be: k =-\frac{-5}{5}= 1

Therefore, the x-axis divides the line in the ratio 1:1 and the point will be,

Putting the value of k=1 in section formula.

P(x,0) = \left ( \frac{x_{2}+x_{1}}{2}, 0 \right )

P(x,0) = \left ( \frac{1-4}{2}, 0 \right ) = \left ( \frac{-3}{2}, 0 \right )

Q6 If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.

Answer:

Let the given points A(1,2),\ B(4,y),\ C(x,6),\ D(3,5) .

Since the diagonals of a parallelogram bisect each other. Intersection point O of diagonal AC and BD also divides these diagonals.

Therefore, O is the mid-point of AC and BD.

The coordinates of the point O when it is mid-point of AC.

\left ( \frac{1+x}{2}, \frac{2+6}{2} \right ) \Rightarrow \left ( \frac{x+1}{2}, 4 \right )

The coordinates of the point O when it is mid-point of BD.

\left ( \frac{4+3}{2}, \frac{5+y}{2} \right ) \Rightarrow \left ( \frac{7}{2}, \frac{5+y}{2} \right )

Since both coordinates are of same point O.

Therefore,

\frac{x+1}{2} =\frac{7}{2} and 4 = \frac{5+y}{2}

Or,

x = 6\ and\ y = 3

Q7 Find the coordinates of point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).

Answer:

As the centre point C(2,-3) will be the mid-point of the diameter AB.

Then, the coordinates of point A will be A(x,y) .

Given point B(1,4) .

Therefore,

(2,-3) = \left ( \frac{x+1}{2}, \frac{y+4}{2} \right )

\frac{x+1}{2} = 2\ and\ \frac{y+4}{2} = -3

\Rightarrow x = 3\ and\ y = -10 .

Therefore, the coordinates of A are (3,-10).

Q8 If A and B are (- 2, - 2) and (2, - 4), respectively, find the coordinates of P such that AP = 3 AB 7 and P lies on the line segment AB.

Answer:

From the figure:

1638427203509

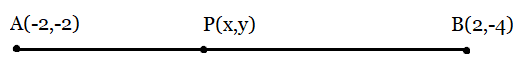
As AP = \frac{3}{7}AB

\Rightarrow PB = \frac{4}{7}AB hence the ratio is 3:4,

Now, from the section formula, we can find the coordinates of Point P.

Section Formula:

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

P(x,y)= \left (\frac{3(2)+4(-2)}{3+4} , \frac{3(-4)+4(-2)}{3+4} \right )

P(x,y)= \left (\frac{6-8}{7} , \frac{-12-8}{7} \right )

P(x,y)= \left (\frac{-2}{7} , \frac{-20}{7} \right )

Q9 Find the coordinates of the points which divide the line segment joining A (– 2, 2) and B(2, 8) into four equal parts.

Answer:

From the figure:

1638427222556

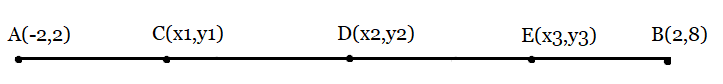
Points C, D, and E divide the line segment AB into four equal parts.

Now, from the section formula, we can find the coordinates of Point C, D, and E.

Section Formula:

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Here point D divides the line segment AB into two equal parts hence

D(x_{2},y_{2})= \left (\frac{-2+2}{2} , \frac{2+8}{2} \right )

D(x_{2},y_{2})= \left (0 , 5 \right )

Now, point C divides the line segment AD into two equal parts hence

C(x_{1},y_{1})= \left (\frac{-2+0}{2} , \frac{2+5}{2} \right )

C(x_{2},y_{2})= \left (-1 , \frac{7}{2} \right )

Also, point E divides the line segment DB into two equal parts hence

E(x_{1},y_{1})= \left (\frac{2+0}{2} , \frac{8+5}{2} \right )

E(x_{2},y_{2})= \left (1 , \frac{13}{2} \right )

Q10 Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order.

Answer:

From the figure:

1638427243029

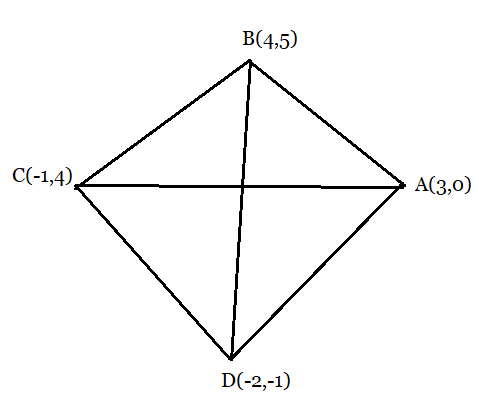
Let the vertices of the rhombus are:

A(3,0),\ B(4,5),\ C(-1,4),\ D(-2,-1)

Area of the rhombus ABCD is given by;

= \frac{1}{2}\times(Product\ of\ lengths\ of\ diagonals)

Hence we have to find the lengths of the diagonals AC and BD of the rhombus.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

Length of the diagonal AC:

AC = \sqrt{(3-(-1))^2+(0-4)^2} = \sqrt{16+16} = 4\sqrt{2}

Length of the diagonal BD:

BD = \sqrt{(4-(-2))^2+(5-(-1))^2} = \sqrt{36+36} = 6\sqrt{2}

Thus, the area will be,

= \frac{1}{2}\times (AC)\times(BD)

= \frac{1}{2}\times (4\sqrt{2})\times(6\sqrt{2}) = 24\ square\ units.


Class 10 maths ch 7 solutions Exercise: 7.3

Q 1 (i) Find the area of the triangle whose vertices are : (2, 3), (–1, 0), (2, – 4)

Answer:

As we know, the area of a triangle with vertices (x1,x2) ,(y1, y2) and (z1 z2 ) is given by :

A= \frac{1}{2}(x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2))

So Area of a triangle whose vertices are(2, 3), (–1, 0)and (2, – 4) is

A= \frac{1}{2}[2(0-(-4))+(-1)(-4-3)+2(3-0)]

A= \frac{1}{2}[8+7+6]

A= \frac{1}{2}[21]

A= \frac{21}{2}

A= 10.5\:unit^2

Hence, the area of the triangle is 10.5 per unit square.

Q1 (ii) Find the area of the triangle whose vertices are (–5, –1), (3, –5), (5, 2)

Answer:

From the figure:

1638427297678

Area of the triangle is given by:

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

Substituting the values in the above equation, we obtain

Area = \frac{1}{2}\left [ (-5)((-5)-(-2))+3(2-(1))+5(-1-(-5)) \right ]

= \frac{1}{2}\left [ 35+9+20 \right ] = 32 \ square\ units.

Q2 (i) In each of the following find the value of ‘k’, for which the points are collinear. (7, –2), (5, 1), (3, k)

Answer:

The points (7, –2), (5, 1), (3, k) are collinear if the area of the triangle formed by the points will be zero.

Area of the triangle is given by:

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ] = 0

Substituting the values in the above equation, we obtain

\frac{1}{2}\left [ 7(1-k)+5(k-(-2))+3(-2-1) \right ] = 0

\left [ 7-7k+5k+10-9 \right ] = 0

\Rightarrow -2k+8 = 0

\Rightarrow k = 4

Hence, the points are collinear for k=4 .

Q2 (ii) In each of the following find the value of ‘k’, for which the points are collinear. (8, 1), (k, – 4), (2, –5)

Answer:

The points (8,1), (k, -4), (2,-5) are collinear if the area of the triangle formed by these points will be zero.

Area of the triangle is given by:

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ] = 0

Substituting the values in the above equation, we obtain

\frac{1}{2}\left [ 8(-4-(-5))+k((-5)-1)+2(1-(-4)) \right ] = 0

\Rightarrow 8-6k+10 = 0

\Rightarrow 6k = 18

\Rightarrow k = 3

Hence, the points are collinear for k = 3 .

Q3 Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Answer:

From the figure:

1638427329430

The coordinates of the point P, Q, and R are:

Point P is the midpoint of side AB, hence the coordinates of P are :

P(x_{1},y_{1}) = \left (\frac{0+2}{2}, \frac{3+1}{2} \right ) = \left (1, 2 \right )

Point Q is the midpoint of side AC, hence the coordinates of Q are :

Q(x_{2},y_{2}) = \left (\frac{2+0}{2}, \frac{1-1}{2} \right ) = \left (1, 0 \right )

Point R is the midpoint of side BC, hence the coordinates of R are :

R(x_{3},y_{3}) = \left (\frac{0+0}{2}, \frac{-1+3}{2} \right ) = \left (0, 1 \right )

Hence, the area of the triangle formed by the midpoints PQR will be,

Area_{(PQR)} = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

= \frac{1}{2}\left [ (2-1)+1(1-0)+0(0-2) \right ]

=\frac{1}{2}(1+1) = 1\ square\ units.

And the area formed by the triangle ABC will be:

Area_{(ABC)} = \frac{1}{2}\left [ 0(1-3)+2(3-(-1))+0(-1-1) \right ]

= \frac{1}{2}\left [ 8 \right ] = 4\ square\ units.

Thus, the ratio of Area of \triangle PQR to the Area of \triangle ABC will be 1:4 .

Q4 Find the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5), (3, – 2) and (2, 3).

Answer:

From the figure:

1638427363305

The coordinates are A(-4,-2),\ B(-3,-5),\ C(3,-2)\ and\ D(2,3)

Divide the quadrilateral into 2 parts of triangles.

Then the area will be, ABC + ADC

Area of the triangle formed by ABC will be,

Area_{(ABC)} = \frac{1}{2}\left [ (-4)((-5)-(-2))+(-3)((-2)-(-2))+3((-2)-(-2)) \right ] = \frac{1}{2}\left [ 12+0+9 \right ] = \frac{21}{2}\ Square\ units.

Area of the triangle formed by ADC will be,

Area_{(ADC)} = \frac{1}{2}\left [ (-4)((-2)-(-3))+3(3-(-2))+2((-2)-(-2)) \right ] = \frac{1}{2}\left [ 20+15+0 \right ] = \frac{35}{2}\ Square\ units.

Therefore, the area of the quadrilateral will be:

= \frac{21}{2}+\frac{35}{2} = 28\ square\ units.

Alternatively,

The points A and C are in the same ordinates.

Hence, the length of base AC will be (3-(-4)) = 7\ units.

Therefore,

Area of triangle ABC:

= \frac{1}{2} \times (Base) \times (Height) = \frac{1}{2}\times(7)(3)

Area of triangle ADC:

= \frac{1}{2} \times (Base) \times (Height) = \frac{1}{2}\times(7)(5)

Therefore, the area will be, \frac{1}{2}\times(7)\times(5+3) =28\ square\ units.

Q5 You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for D ABC whose vertices are A(4, – 6), B(3, –2) and C(5, 2).

Answer:

From the figure:

1638427386798

The coordinates of midpoint M of side BC is:

M = \left ( \frac{3+5}{2}, \frac{-2+2}{2} \right ) = \left ( 4,0 \right )

Now, calculating the areas of the triangle ABM and ACM :

Area of triangle, ABM:

Area_{(ABM)} = \frac{1}{2}\left [ 4((-2)-0)+3(0-(-6))+4((-6)-(-2)) \right ]

= \frac{1}{2}\left [ -8+18-16 \right ] = 3\ Square\ units.

Area of triangle, ACM:

Area_{(ACM)} = \frac{1}{2}\left [ 4(0-(-2))+4(2-(-6))+5((-6)-0) \right ]

= \frac{1}{2}\left [ -8+32-30 \right ] = -3\ Square\ units.

However, the area cannot be negative, Therefore, area of \triangle ACM is 3 square units.

Clearly, the median AM divided the \triangle ABC in two equal areas.


Chapter 7 maths class 10 ncert solutions Exercise: 7.4

Q1 Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).

Answer:

Let the line divide the line segment AB in the ratio k:1 at point C.

Then, the coordinates of point C will be:

C(x,y) = \left ( \frac{3k+2}{k+1},\frac{7k-2}{k+1} \right )

Point C will also satisfy the given line equation 2x + y - 4 = 0 , hence we have

\Rightarrow 2\left ( \frac{3k+2}{k+1} \right )+\left (\frac{7k-2}{k+1} \right ) - 4 = 0

\Rightarrow \frac{6k+4+7k-2-4k-4}{k+1} = 0

\Rightarrow 9k-2 = 0

\Rightarrow k=\frac{2}{9}

Therefore, the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points A(2,-2) and B(3,7) is 2:9 internally.

Q2 Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.

Answer:

If the points (x, y), (1, 2)\ and\ (7, 0) are collinear then, the area formed by these points will be zero.

The area of the triangle is given by,

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ] = 0

Substituting the values in the above equation, we have

Area = \frac{1}{2}\left [ x(2-0)+1(0-y)+7(y-2) \right ]= 0

\Rightarrow 2x-y+7y-14= 0

Or,

\Rightarrow x+3y-7= 0

Hence, the required relation between x and y is x+3y-7= 0 .

Q3 Find the center of a circle passing through the points (6, – 6), (3, – 7) and (3, 3).

Answer:

From the figure:

1638427419480

Let the center point be O(x,y) .

Then the radii of the circle OA,\ OB,\ and\ OC are equal.

The distance OA:

OA = \sqrt{(x-6)^2+(y+6)^2}

The distance OB:

OB = \sqrt{(x-3)^2+(y+7)^2}

The distance OC:

OC = \sqrt{(x-3)^2+(y-3)^2}

Equating the radii of the same circle.

When equating, OA = OB

\sqrt{(x-6)^2+(y+6)^2}= \sqrt{(x-3)^2+(y+7)^2}

Squaring both sides and applying a^2-b^2 = (a+b)(a-b)

\Rightarrow (x-6+x-3)(x-6-x+3)+(y+6+y+7)(y+6-y-7) = 0

\Rightarrow (2x-9)(-3) + (2y+13)(-1) = 0

\Rightarrow -6x+27-2y-13 = 0 or

\Rightarrow 3x+y -7= 0 ...................................(1)

When equating, OA = OC

\sqrt{(x-6)^2+(y+6)^2}= \sqrt{(x-3)^2+(y-3)^2}

Squaring both sides and applying a^2-b^2 = (a+b)(a-b)

\Rightarrow (x-6+x-3)(x-6-x+3)+(y+6+y-3)(y+6-y+3) = 0

\Rightarrow (2x-9)(-3) + (2y+3)(9) = 0

\Rightarrow -3x+9y+27 = 0 ...................................(2)

Now, adding the equations (1) and (2), we get

\Rightarrow 10y = -20

\Rightarrow y = -2 .

From equation (1), we get

\Rightarrow 3x-2 = 7

\Rightarrow 3x =9

\Rightarrow x =3

Therefore, the centre of the circle is (3,-2) .

Q4 The two opposite vertices of a square are (–1, 2) and (3, 2). Find the coordinates of the other two vertices.

Answer:

From the figure:

1638427461655

We know that the sides of a square are equal to each other.

Therefore, AB = BC

So,

\sqrt{(x-1)^2+(y-2)^2} = \sqrt{(x-3)^2+(y-2)^2}

Squaring both sides, we obtain

\implies (x-1)^2+(y-2)^2 = (x-3)^2+(y-2)^2

Now, doing \left ( a^2-b^2 = (a+b)(a-b) \right )

We get

\implies (x-1+x-3)(x-1-x+3) = 0

Hence x = 2 .

Applying the Pythagoras theorem to find out the value of y.

AB^2+BC^2 = AC^2

(\sqrt{(2-1)^2+(y-2)^2})^2 + (\sqrt{(2-3)^2+(y-2)^2})^2 = (\sqrt{(3+1)^2+(2-2)^2})^2

\Rightarrow \left (\sqrt{1+(y-2)^2} \right )^2 + \left (\sqrt{1+(y-2)^2} \right )^2 = \left (\sqrt{16} \right )^2

\Rightarrow (y-2)^2 = 7

Q5 (i) The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar is planted on the boundary at a distance of 1m from each other. There is a triangular grassy lawn in the plot as shown in Fig. 7.14. The students are to sow seeds of flowering plants on the remaining area of the plot. (i) Taking A as origin, find the coordinates of the vertices of the triangle.

1638427489636

Answer:

Taking A as origin then, the coordinates of P, Q, and R can be found by observation:

Coordinates of point P is (4,6).

Coordinates of point Q is (3,2).

Coordinates of point R is (6,5).

The area of the triangle, in this case, will be:

Area =\frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

=\frac{1}{2}\left [ 4(2-5)+3(5-6)+6(6-2) \right ]

=\frac{1}{2}\left [ -12-3+24\right ] = \frac{9}{2}\ Square\ units.

Q5 (ii) The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar is planted on the boundary at a distance of 1m from each other. There is a triangular grassy lawn in the plot as shown in Fig. 7.14. The students are to sow seeds of flowering plants on the remaining area of the plot. (ii) What will be the coordinates of the vertices of D PQR if C is the origin? Also, calculate the areas of the triangles in these cases. What do you observe?


1638427504689

Answer:

Taking C as origin, then CB will be x-axis and CD be y-axis.

The coordinates fo the vertices P, Q, and R are: (12,2),\ (13,6),\ (10,3). respectively.

The area of the triangle, in this case, will be:

Area =\frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

=\frac{1}{2}\left [ 12(6-3)+13(3-2)+10(2-6) \right ]

=\frac{1}{2}\left [ 36-13+40 \right ] = \frac{9}{2}\ Square\ units.

It can be observed that in both cases the area is the same so, it means that the area of any figure does not depend on the reference which you have taken.

Q6 The vertices of a \Delta ABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that \frac{AD }{AB} = \frac{AE }{AC } = \frac{1}{4} Calculate the area of the \Delta ADE and compare it with the area of \Delta ABC .

Answer:

From the figure:

1638427528989

Given ratio:

\frac{AD }{AB} = \frac{AE }{AC } = \frac{1}{4}

Therefore, D and E are two points on side AB and AC respectively, such that they divide side AB an AC in the ratio of 1:3 .

Section formula:

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Then, coordinates of point D:

D(x_{1},y_{1})= \left (\frac{1\times1+3\times 4}{1+3} , \frac{1\times 5+3\times 6}{1+3} \right )

Coordinates of point E:

E(x_{2},y_{2})= \left (\frac{1\times7+3\times 4}{1+3} , \frac{1\times 2+3\times 6}{1+3} \right )

= \left ( \frac{19}{4}, \frac{20}{4} \right )

Then, the area of a triangle:

= \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

Substituting the values in the above equation,

Area\ of\ \triangle ADE = \frac{1}{2}\left [ 4\left ( \frac{23}{4} - \frac{20}{4}\right )+\frac{13}{4}\left ( \frac{20}{4} - 6 \right )+\frac{19}{4}\left (6-\frac{23}{4} \right )\right ] = \frac{1}{2}\left [ 3-\frac{13}{4} +\frac{19}{16}\right ] = \frac{1}{2}\left [ \frac{48-52+19}{16} \right ] = \frac{15}{32}\ square\ units.

Area\ of\ \triangle ABC = \frac{1}{2}\left [ 4(5-2)+1(2-6)+7(6-5) \right ]

= \frac{1}{2}\left [ 12-4+7 \right ] = \frac{15}{2}\ Square\ units.

Hence the ratio between the areas of \triangle ADE and \triangle ABC is 1:16.

Q7 (1) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of \triangle ABC . The median from A meets BC at D. Find the coordinates of the point D.

Answer:

From the figure:

1638427550821

Let AD be the median of the triangle

Then, D is the mid-point of BC

Coordinates of Point D:

\left ( \frac{6+1}{2},\frac{5+4}{2} \right ) = \left ( \frac{7}{2}, \frac{9}{2} \right )

Q7 (ii) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of D ABC. Find the coordinates of the point P on AD such that AP: PD = 2: 1

Answer:

From the figure,

1638427579264

The point P divides the median AD in the ratio, AP: PD = 2: 1

Hence using the section formula,

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

P(x,y)= \left (\frac{2\times\frac{7}{2}+1\times4}{2+1} , \frac{2\times\frac{9}{2}+1\times2}{2+1} \right ) = \left ( \frac{11}{3}, \frac{11}{3} \right )

Q7 (iii) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of D ABC. Find the coordinates of points Q and R on medians BE and CF respectively such that BQ: QE = 2: 1 and CR: RF = 2: 1

Answer:

From the figure,

1638427609335

\Rightarrow The point Q divides the median BE in the ratio, BQ : QE = 2 : 1

Hence using the section formula,

Q(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Q(x,y)= \left (\frac{2\times\frac{5}{2}+1\times6}{2+1} , \frac{2\times3+1\times5}{2+1} \right ) = \left ( \frac{11}{3}, \frac{11}{3} \right )

\Rightarrow The point R divides the median CF in the ratio, CR: RF = 2: 1

Hence using the section formula,

R(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

R(x,y)= \left (\frac{2\times 5+1\times1}{2+1} , \frac{2\times\frac{7}{2}+1\times4}{2+1} \right ) = \left ( \frac{11}{3}, \frac{11}{3} \right )

Q7 (iv) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of D ABC. What do you observe?

Answer:

We observed that the coordinates of P, Q, and R are the same. Therefore, all these are representing the same point on the plane. i.e., the centroid of the triangle.

Q7 (v) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of \triangle ABC . If A(x_1, y_1), B(x_2, y_2)\ and\ C(x_3, y_3) are the vertices of \triangle ABC , find the coordinates of the centroid of the triangle.

Answer:

From the figure, triangle-median-d

Let the median be AD which divides the side BC into two equal parts.

Therefore, D is the mid-point of side BC.

Coordinates of D:

= \left ( \frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2} \right )

Let the centroid of this triangle be O.

Then, point O divides the side AD in a ratio 2:1.

Coordinates of O:

= \left ( \frac{2\times\frac{x_{2}+x_{3}}{2}+1\times x_{1}}{2+1}, \frac{2\times\frac{y_{2}+y_{3}}{2}+1\times y_{1} }{2+1} \right )

= \left ( \frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3} \right )

Q8 ABCD is a rectangle formed by the points A(–1, –1), B(– 1, 4), C(5, 4) and D(5, – 1). P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.

Answer:

From the figure:

1638427884180

P is the mid-point of side AB.

Therefore, the coordinates of P are, \left ( \frac{-1-1}{2}, \frac{-1+4}{2} \right ) = \left ( -1, \frac{3}{2} \right )

Similarly, the coordinates of Q, R and S are: \left ( 2,4 \right ),\ \left ( 5, \frac{3}{2} \right ),\ and\ \left ( 2,-1 \right ) respectively.

The distance between the points P and Q:

PQ = \sqrt{(-1-2)^2+\left ( \frac{3}{2} -4 \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

and the distance between the points Q and R:

QR = \sqrt{(2-5)^2+\left ( 4-\frac{3}{2} \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

Distance between points R and S:

RS = \sqrt{(5-2)^2+\left ( \frac{3}{2}+1 \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

Distance between points S and P:

SP = \sqrt{(2+1)^2+\left ( -1-\frac{3}{2} \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

Distance between points P and R the diagonal length:

PR = \sqrt{(-1-5)^2+\left ( \frac{3}{2}-\frac{3}{2} \right )^2} = 6

Distance between points Q and S the diagonal length:

QS = \sqrt{(2-2)^2+\left ( 4+1 \right )^2} = 5

Hence, it can be observed that all sides have equal lengths. However, the diagonals are of different lengths.

Therefore, PQRS is a rhombus.

Summary Of Class 10 maths NCERT solutions chapter 7

Coordinate Geometry is one of the important chapters for higher mathematics in upcoming classes. You will use at least some part of coordinate geometry in the field whether you are going to study commerce, engineering, maths, medical, arts, etc. Class 10 NCERT solutions Maths chapter 7 is designed to give you a step by step solution for a particular question. In Coordinate Geometry, you will study the algebraic forms of geometric figures. There are four exercises to solve from the NCERT book chapter 7 Maths Class 10. The exercises are listed below

Key Features of class 10 maths ncert solutions chapter 7

The NCERT class 10 Coordinate Geometry includes several key features to aid students in their understanding and practice of the material.

  • Class 10 maths chapter 7 example 9 provide answers to all exercise questions in the NCERT textbook.

  • Class 10 maths ch 7 solutions include diagrams and alternate methods to help students understand the concepts.

  • Chapter 7 maths class 10 pdf solutions help to familiarise students with important formulas and standards.

  • Class 10 chapter 7 ncert solutions include a variety of examples to help students connect the geometry and numerical concepts to real-life scenarios.

  • Memorise the formula to find out some directly asked questions.

NCERT Solutions for Class 10 Maths - Chapter Wise

How to use NCERT Solutions for Class 10 maths chapter 7 Coordinate Geometry?

Students can follow the steps provided below to use the class 10 maths ncert solutions chapter 7 in the best way possible.

  • Go through the concepts and examples given in the textbook to understand the basics of the chapter.

  • Memorize the formula to find out some directly asked questions.

  • During the practice of exercises, you can take the help of NCERT solutions for class 10 Maths chapter 7.

  • Now, students can practice the previous year's question to boost your preparation.

Benefits of NCERT Solutions for Class 10 maths chapter 7 Coordinate Geometry

  • Students will be able to study in a strategic way after accessing Class 10 Maths NCERT solutions chapter 7.

  • Class 10 Maths chapter 7 NCERT solutions are solved by the subject-matter experts and are very reliable at the same time.

  • NCERT solutions for class 10 maths chapter 7 Coordinate Geometry is designed to give the students step by step solution for a particular question.

  • In Coordinate Geometry, students will study the algebraic forms of geometric figures.

NCERT solutions of class 10 subject wise

NCERT Exemplar solutions - Subject wise

Frequently Asked Questions (FAQs)

1. How are coordinate geometry class 10 solutions helpful for CBSE exams?

The chapter 7 maths class 10 ncert solutions are designed to align with the current CBSE syllabus and include detailed explanations for each question. Practising these NCERT solutions for Class 10 Maths will help students improve their exam skills and time management, making them more likely to score well on the exam. Additionally, working through these solutions of maths chapter 7 class 10 can help students become more familiar with the exam format, giving them more confidence when taking the test.

2. Mention the topics that are covered in NCERT Solutions for Class 10 Maths Chapter 7.

NCERT coordinate geometry class 10 ncert solutions covers several key topics, including Introduction to Coordinate Geometry, Distance Formula, Section Formula, and Area of the Triangle. Through a thorough study of these solutions of class 10 chapter 7 maths, students will gain the skills necessary to easily solve complex problems related to these topics.

3. Is it necessary to practise all the exercises presented in class 10 maths chapter 7 solutions?

Yes, It is essential to practise all the exercises in coordinate geometry class 10 chapter 7 Maths because they include a variety of questions that may appear in the CBSE board examination. By solving these exercises of chapter 7 class 10 maths, students will increase their chances of success on the final exams and feel more confident when taking the test. You can also study NCERT solutions for class 10 maths chapter 7 in hindi medium if you are facing issue with english medium. 

4. How to master the CBSE class 10 Maths?

First, you should try to solve every problem on your own including examples given in the NCERT textbook. Once you complete the entice syllabus, you must solve CBSE previous years paper in order to get familiar with the exam. For ease students can download chapter 7 Maths class 10 pdf solutions and study both online and offline mode.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 812 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
IBM
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST
CBSE conducts surprise inspections at 27 schools in Rajasthan, Delhi to curb menace of dummy schools
September 03, 2024 - 03:02 PM IST

Stay up-to date with CBSE Class 10th News

Back to top