How To Prepare Work And Energy For NSEJS

Tips To Prepare Work And Energy For NSEJS

• Be thorough with NCERT Class 9 Work And Energy concepts.

• Solve NCERT exemplar problems and previous year's NSEJS question paper

NSEJS: Important Points For Work Energy And Power

Let's discuss important concepts as well as work power and energy formulas.

Work

What do you understand about the term “work”? The term work is different from how it is used in daily life and we use it in science. Let's take an example, you are pushing a heavy rock but it does not move despite making all efforts and you get exhausted. In day to day life, you are working hard but in science, you haven't done any work on the rock as there is no displacement in the heavy rock. The term work is defined and used differently in science. Let's discuss it in detail.

Scientific Conception Of Work

Consider an example to understand the term work in view of science. A child is pulling a cart. s/he is applying a force and the cart is moving. Therefore work is done by the child on the cart.

In another example, a person is lifting a wooden block. S/he is lifting the block against the gravitational force of the earth. Here in this example force is applied by the person as well as by gravity. Block is lifting up so therefore the work is done by both the person and by the gravitational force of Earth.

Thus if there is any work then the following conditions must be followed.

• Force should not be zero.

• Displacement should not be zero.

If force or displacement is zero then work must be zero.

Work Done By A Constant Force

Work is a scalar quantity so it does not have direction, it only has magnitude. The following are three cases. Let's discuss them one by one.

Case 1: Force acting in the direction of displacement.

A constant force is acting on an object in the direction of displacement. Here, in this case, work done by the force is calculated by the multiplication of force and displacement.

Work = force x Displacement.

W = F x S

Here W = work, F = force, S = displacement.

If the magnitude of the force is 2 newtons and the displacement is 5 meters. Then work done by the force is 2 x 5 = 10 Joule.

Case 2: Force acting in the opposite direction of displacement.

A person is lifting an object. The earth's gravitational force is acting in the opposite direction of displacement. In this case, work done by the force is calculated by the negative multiplication of force and displacement.

Work = - Force x Displacement

W = - F x S

If the force applied by the gravitational force of the earth is 10 Newton and the lifting height is 1 meter then work done by the gravitational force is - 10 x 1 = -10 Joule.

Case 3: the angle between force and displacement is θ degree.

In this case, work done by the force is calculated by

Work = Force x Displacement in direction of force

W = F. S Cosθ

Thus, work is considered positive if the direction of displacement and force are the same. If the displacement is in the opposite direction of force then it is considered negative.

Energy

The term energy is very often used in our life. It is so essential that without it there will be no life on earth. The biggest source of energy is the Sun. The energy is nothing but the ability to do work. There are different forms of energy like kinetic energy, potential energy, light energy, heat energy, sound energy, etc. we can neither create energy nor we can destroy only we can convert it from one form of energy to another form of energy. It means the energy of an isolated system is always conserved. Now let's discuss the different forms of energy.

Kinetic Energy

A moving object like a rotating wheel, moving bullet, or blowing wind can do work. Kinetic energy is energy stored in a moving body. In other words, it is an ability to do work by a moving body. A rolling stone, a falling apple, a speeding bike, flowing water, a flying aircraft blowing wind, a running athlete, etc. possess kinetic energy. A body moving faster can do more work comparatively than a body moving slowly.

We know that

F = Ma, where a is acceleration.

And v² = u² + 2aS

S = (v² - u²) / (2a)

Work = F x S

Work = (Ma) x (v² - u²) / (2a)

If an object starts from rest then u = 0

Work = ½ M v²

Hence, the kinetic energy of an object of mass M moving with velocity V is given by ½ M (V)^2

K.E = ½ M(v)²

K.E = P² / (2M), Here Momentum of body P = Mv

Potential Energy

A stretched rubber, an extended or compressed spring, a lifted object, etc can do work because they have energy. When the work is done by an external force on an object then it is stored in the object if it is not used to cause a change in the velocity. This stored form of energy is known as potential energy. It is always defined respectively. We can only calculate the change in potential energy.

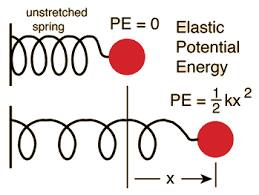
Elastic Potential Energy

Suppose the potential energy of an un stretched spring is 0 and a spring is stretched or compressed by x, then the potential energy stored in the spring is given by P.E = ½ k. (x)^2 where k is spring constant.

Potential Energy Of An Object At A Height

When an object is lifted up, the work is done against gravity and it is stored as potential energy known as gravitational potential energy. Just take potential energy at the ground as zero. If a mass m is lifted at height h then potential energy stored in the mass is given by

P.E = potential energy at height h - potential energy at ground

P.E = mgh - 0

P.E = mgh

Work done by the gravitational force is negative of potential energy stored in the object. Gravitational force is a conservative force which means work done by the gravitational force does not depend on the path followed by the object. It only depends on the initial and final position of the object. Potential energy for following both path is same and equal to mgh

Thus, it can be said that potential energy is negative of work done by conservative force.

Power:

Power is defined as the rate of doing work. It can be calculated as

Power = work / time

P = w / t

Unit of power is joule per second or watt.

1 watt = 1 joule per second.

1 kw = 1000 watt

1 kw = 1000 J / s

In daily life a high amount of energy is used and Joule per second is too small. Thus we have Commercial Unit Of Energy know as “Unit”

1 Unit = 1kwh

1 Unit = 1000 x 3600 seconds

1 Unit = 3.6 x 10⁶ Joule

Practice Previous Year Questions

Q-1

The kinetic energy of a particle moving along a circle of radius R depends upon the distance 2 covered 's' as KE = where a is a constant. The magnitude of the force acting on the particle as a function of 's' is ( NSEJS 2020-21)

Solution:

We know that in a circular path both centripetal acceleration and tangential acceleration are acting therefore

Net acceleration is equal to

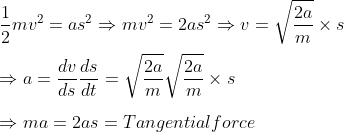
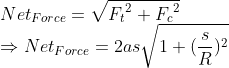
Hence, Option D is correct

Q-2

Two small masses m and M lie on a large horizontal frictionless circular track of radius R. The two masses are free to slide on the track but constrained to move along a circle. Initially the two masses are tied by a thread with a compressed spring between them (spring of negligible length being attached with none of the two masses). The compressed spring stores a potential energy U0. At a certain time t = 0 the thread is burnt and the two masses are released to run opposite to each other leaving the spring behind. The total mechanical energy remains conserved. On the circular track the two masses make a head on perfectly elastic collision. Take M = 2m for all calculations. Which of the following option(s) is / are correct? ( NSEJS 2021-22 )

Solution:

Reference Materials

• NCERT Class 9 Science Book

• NCERT Exemplar Problems From Work And Energy

• NSEJS Previous Year Question Papers