NCERT Solutions for Class 12 Physics Chapter 13 - Nuclei

Answer:

The atomic mass of boron is 10.811 u

Mass of the two stable isotopes are $10.01294 u$ and $11.00931 u$ respectively
Let the two isotopes have abundances $\mathrm{x} \%$ and $(100-\mathrm{x}) \%$

$
\begin{aligned}
& 10.811=\frac{10.01294 \times x+11.00931 \times(100-x)}{100} \\
& x=19.89 \\
& 100-x=80.11
\end{aligned}
$

Therefore the abundance of ${ }_5^{10} \mathrm{~B}$ is $19.89 \%$ and that of ${ }_5^{11} \mathrm{~B}$ is $80.11 \%$

2. The three stable isotopes of neon: $_{10}^{20}\textrm{Ne},$ $_{10}^{21}\textrm{Ne}$ and $_{10}^{22}\textrm{Ne}$ have respective abundances of $90.51\; ^{o}/_{o}$ , $0.27\; ^{o}/_{o}$ and $9.22\; ^{o}/_{o}$ . The atomic masses of the three isotopes are $19.99\; u, 20.99\; u \; \; and\; \; 21.99 \; u,$ respectively. Obtain the average atomic mass of neon.

Answer:

The atomic masses of the three isotopes are $19.99 u\left(m_1\right), 20.99 u\left(m_2\right)$ and $21.99 u\left(m_3\right)$
Their respective abundances are $90.51 \%\left(p_1\right), 0.27 \%\left(p_2\right)$ and $9.22 \%\left(p_3\right)$

$
\begin{aligned}
& m=\frac{19.99 \times 90.51+20.99 \times 0.27+21.99 \times 9.22}{100} \\
& m=20.1771 u
\end{aligned}
$

The average atomic mass of neon is 20.1771 u .

3. (i) Write nuclear reaction equations for

$\; \alpha -decay\; of\; _{88}^{226}\textrm{Ra}$

Answer:

The nuclear reaction equations for the given alpha decay

$_{88}^{226}\textrm{Ra}\rightarrow _{86}^{222}\textrm{Rn}+_{2}^{4}\textrm{He}$

3. (ii) Write nuclear reaction equations for

$\; \alpha -decay\; of\; _{94}^{242}\textrm{Pu}$

Answer:

The nuclear reaction equations for the given alpha decay is

$_{94}^{242}\textrm{Pu}\rightarrow _{92}^{238}\textrm{U}+_{2}^{4}\textrm{He}$

3. (iii) Write nuclear reaction equations for

$\; \beta ^{-} -\: decay\; of\; _{15}^{32}\textrm{P}$

Answer:

The nuclear reaction equations for the given beta minus decay is

$_{15}^{32}\textrm{P}\rightarrow _{16}^{32}\textrm{S}+e^{-}+\bar{\nu }$

3.(iv) Write nuclear reaction equations for

$\; \beta ^{-} -\: decay\; of\; _{83}^{210}\textrm{Bi}$

Answer:

The nuclear reaction equation for the given beta minus decay is

$_{83}^{210}\textrm{Bi}\rightarrow _{84}^{210}\textrm{Po}+e^{-}+\bar{\nu }$

3.(v) Write nuclear reaction equations for

$\; \beta ^{+} -\: decay\; of\; _{6}^{11}\textrm{C}$

Answer:

The nuclear reaction for the given beta plus decay will be

$_{6}^{11}\textrm{C}\rightarrow _{5}^{11}\textrm{P}+e^{+}+\nu$

13.6 (vi) Write nuclear reaction equations for

$\; \beta ^{+} -\: decay\; of\; _{43}^{97}\textrm{Tc}$

Answer:

nuclear reaction equations for

$\beta ^{+} -\: decay\; of\; _{43}^{97}\textrm{Tc}\ is$

$_{43}^{97}\textrm{Tc}\rightarrow _{42}^{97}\textrm{Mo}+e^{+}+\nu$

3.(vii) Write nuclear reaction equations for

Electron capture of $_{54}^{120}\textrm{Xe}$

Answer:

The nuclear reaction for electron capture of $_{54}^{120}\textrm{Xe}$ is

$_{54}^{120}\textrm{Xe}+e^{-}\rightarrow _{53}^{120}\textrm{I}+\nu$

4. A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, and b) 1% of its original value?

Answer:

(a) The activity is proportional to the number of radioactive isotopes present

The number of half years in which the number of radioactive isotopes reduces to x% of its original value is n.

$n=log_{2}(\frac{100}{x})$

In this case

$n=log_{2}(\frac{100}{3.125})=log_{2}32=5$

It will take 5T years to reach 3.125% of the original activity.

(b) In this case

$n=log_{2}(\frac{100}{1})=log_{2}100=6.64$

It will take 6.64T years to reach 1% of the original activity.

5. The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive $_{6}^{14}\textrm{C}$ present with the stable carbon isotope $_{6}^{12}\textrm{C}$ . When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of $_{6}^{14}\textrm{C}$, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of $_{6}^{14}\textrm{C}$ dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilization.

Answer:

Since we know that activity is proportional to the number of radioactive isotopes present in the sample.

$
\frac{R}{R_0}=\frac{N}{N_0}=\frac{9}{15}=0.6
$

Also

$
\begin{aligned}
& N=N_0 e^{-\lambda t} \\
& t=-\frac{1}{\lambda} \ln \frac{N}{N_0} \\
& t=-\frac{1}{\lambda} \ln 0.6 \\
& t=\frac{0.51}{\lambda}
\end{aligned}
$

but $\lambda=\frac{0.693}{T_{1 / 2}}$
Therefore

$
\begin{aligned}
& t=0.51 \times \frac{T_{1 / 2}}{0.693} \\
& t=0.735 T_{1 / 2} \\
& t \approx 4217
\end{aligned}
$

The age of the Indus-Valley civilisation, calculated using the given specimen, is approximately 4217 years.

6. Obtain the amount of $_{27}^{60}\textrm{Co}$ necessary to provide a radioactive source of 8.0 mCi strength. The half-life of $_{27}^{60}\textrm{Co}$ is 5.3 years.

Answer:

Required activity $=8.0 \mathrm{mCi}$
$1 \mathrm{Ci}=3.7 \times 10^{10}$ decay s $\mathrm{s}^{-1}$
$8.0 \mathrm{mCi}=8 \times 10^{-3} \times 3.7 \times 10^{10}=2.96 \times 10^8$ decay s ${ }^{-1}$
$T_{1 / 2}=5.3$ years

$
\lambda=\frac{0.693}{T_{1 / 2}}
$

$
\lambda=\frac{0.693}{5.3 \times 365 \times 24 \times 3600}
$

$
\lambda=4.14 \times 10^{-9} s^{-1}
$

$
\frac{\mathrm{d} N}{\mathrm{~d} t}=-N \lambda
$

$
N=-\frac{\mathrm{d} N}{\mathrm{~d} t} \times \frac{1}{\lambda}
$

$
N=-\left(-2.96 \times 10^8\right) \times \frac{1}{4.14 \times 10^{-9}}
$

$
N=7.15 \times 10^{16} \text { atoms }
$

Mass of those many atoms of Cu will be

$
\begin{aligned}
& w=\frac{7.15 \times 10^{16} \times 60}{6.023 \times 10^{23}} \\
& w=7.12 \times 10^{-6} g
\end{aligned}
$

$7.12 \times 10^{-6} \mathrm{~g}$ of ${ }_{27}^{60} \mathrm{Co}$ is necessary to provide a radioactive source of 8.0 mCi strength.

7. The half-life of $_{38}^{90}\textrm{Sr}$ is 28 years. What is the disintegration rate of 15 mg of this isotope?

Answer:

$T_{1 / 2}=28$ years

$
\begin{aligned}
\lambda & =\frac{0.693}{28 \times 365 \times 24 \times 3600} \\
\lambda & =7.85 \times 10^{-10} \text { decay } \mathrm{s}^{-1}
\end{aligned}
$

The number of atoms in 15 mg of ${ }_{38}^{90} \mathrm{Sr}$ is

$
\begin{aligned}
& N=\frac{15 \times 10^{-3} \times 6.023 \times 10^{23}}{90} \\
& N=1.0038 \times 10^{20}
\end{aligned}
$

The disintegration rate will be

$
\begin{aligned}
& \frac{\mathrm{d} N}{\mathrm{~d} t}=-N \lambda \\
& =-1.0038 \times 10^{20} \times 7.85 \times 10^{-10} \\
& =-7.88 \times 10^{10} \mathrm{~s}^{-1}
\end{aligned}
$

The disintegration rate is therefore $7.88 \times 10^{10}$ decay $\mathrm{s}^{-1}$.

8.(a) Find the Q-value and the kinetic energy of the emitted $\alpha$ -particle in the $\alpha$ -decay of

9. The radionuclide $^{11}C$ decays according to

$_{6}^{11}\textrm{C}\rightarrow B+e^{+}+v:T_{1/2}=20.3\; min$
The maximum energy of the emitted positron is $0.960\; MeV.$ .

Given the mass values:

$m(_{6}^{11}\textrm{C})=11.011434\; u$ and $m(_{6}^{11}\textrm{B})=11.009305\; u$
calculate Q and compare it with the maximum energy of the positron emitted.

Answer:

If we use atomic masses

$\\\Delta m=m(_{6}^{11}\textrm{C})-m(_{5}^{11}\textrm{B})-2m_{e}\\ $
$\Delta m=11.011434-11.009305-2\times 0.000548\\ $
$\Delta m=0.001033u$

Q-value= 0.001033 $\times$ 931.5=0.9622 MeV, which is comparable with the maximum energy of the emitted positron.

10. The nucleus $_{10}^{23}\textrm{Ne}$ decays by $\beta ^{-}$ emission. Write down the $\beta$ -decay equation and determine the maximum kinetic energy of the electrons emitted. Given that:

$(i) m (_{10}^{23}\textrm{Ne} ) = 22.994466 \; u$

$(ii) m (_{11}^{23}\textrm{Na} ) = 22.089770 \; u$

Answer:

The $\beta$ decay equation is

$_{10}^{23}\textrm{Ne}\rightarrow _{11}^{23}\textrm{Na}+e^{-}+\bar{\nu }+Q$

$\\\Delta m=m(_{10}^{23}\textrm{Ne})-_{11}^{23}\textrm{Na}-m_{e}\\ $
$\Delta m=22.994466-22.989770\\ $
$\Delta m=0.004696u$

(we did not subtract the mass of the electron, as it is cancelled because of the presence of one more electron in the sodium atom)

Q=0.004696 $\times$ 931.5

Q=4.3743 eV

The emitted nucleus is way heavier than the $\beta$ particle and the energy of the antineutrino is also negligible therefore, the maximum energy of the emitted electron is equal to the Q value.

11. A $1000\; MW$ fission reactor consumes half of its fuel in $5.00 \; y$ . How much $_{92}^{235}\textrm{U}$ did it contain initially? Assume that the reactor operates $80\; ^{}o/_{0}$ of the time, that all the energy generated arises from the fission of $_{92}^{235}\textrm{U}$ and that this nuclide is consumed only by the fission process.

Answer:

The amount of energy liberated on fission of 1 $_{92}^{235}\textrm{U}$ atom is 200 MeV.

The amount of energy liberated on fission of 1g $_{92}^{235}\textrm{U}$

$\\=\frac{200\times 10^{6} \times 1.6\times 10^{-19}\times 6.023\times 10^{23}}{235}\\=8.2\times 10^{10}\ Jg^{-1}$

Total Energy produced in the reactor in 5 years

$\\=1000\times 10^{6}\times 0.8\times 5\times 365\times 24\times 3600\\ =1.261\times 10^{17}\ J$

Mass of $_{92}^{235}\textrm{U}$ which underwent fission, m

$=\frac{1.261\times 10^{17}}{8.2\times 10^{10}}$

=1537.8 kg

The amount present initially in the reactor = 2m

=2 $\times$ 1537.8

=3075.6 kg

12. For the $\beta ^{+}$ (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K–shell, is captured by the nucleus and a neutrino is emitted).

$e^{+}+_{z}^{A}\textrm{X}\rightarrow _{Z-1}^{A}\textrm{Y}+v$

Show that if $\beta ^{+}$ emission is energetically allowed, electron capture is necessarily allowed but not vice–versa.

Answer:

For the electron capture, the reaction would be

$_{Z}^{A}\textrm{X}+e^{-}\rightarrow _{Z-1}^{A}\textrm{Y}+\nu +Q_{1}$

The mass defect and q value of the above reaction would be

$\\\Delta m_{1}=m(_{Z}^{A}\textrm{X})+m_{e}-m(_{Z-1}^{A}\textrm{Y})\\ Q_{1}=([m(_{Z}^{A}\textrm{X})-m(_{Z-1}^{A}\textrm{Y})]+m_{e})c^{2}$

where m N $(_{Z}^{A}\textrm{X})$ and m N $(_{Z-1}^{A}\textrm{Y})$ are the nuclear masses of elements X and Y respectively

For positron emission, the reaction would be

$_{Z}^{A}\textrm{X}\rightarrow _{Z-1}^{A}\textrm{Y}+e^{+}+\bar{\nu }+Q_{2}$

The mass defect and q value for the above reaction would be

$\\\Delta m_{2}=m(_{Z}^{A}\textrm{X})-m(_{Z-1}^{A}\textrm{Y})-m_{e}\\ Q_{2}=([m(_{Z}^{A}\textrm{X})-m(_{Z-1}^{A}\textrm{Y})]-m_{e})c^{2}$

From the above values, we can see that if Q 2 is positive, Q 1 will also be positive but Q 1 being positive does not imply that Q 2 will also be positive.

14. (i) The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei $_{20}^{41}\textrm{Ca}$ from the following data:

$m(_{20}^{40}\textrm{Ca})=39.962591\; u$

$m(_{20}^{41}\textrm{Ca})=40.962278 \; u$

$m(_{13}^{26}\textrm{Al})=25.986895 \; u$

$m(_{13}^{27}\textrm{Al})=26.981541 \; u$

Answer:

The reaction showing the neutron separation is

$_{20}^{41}\textrm{Ca}+E\rightarrow _{20}^{40}\textrm{Ca}+_{0}^{1}\textrm{n}$

$\\E=(m(_{20}^{40}\textrm{Ca})+m(_{0}^{1}\textrm{n})-m(_{20}^{41}\textrm{Ca}))c^{2}\\ $
$E=(39.962591+1.008665-40.962278)c^{2}\\ $
$E=(0.008978)u\times c^{2}$

But 1u=931.5 MeV/$c^{2}$

Therefore E=(0.008978) $\times$ 931.5

E=8.363007 MeV

Therefore to remove a neutron from the $_{20}^{41}\textrm{Ca}$ nucleus 8.363007 MeV of energy is required

14. (ii) The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei $_{13}^{27}\textrm{Al}$ from the following data:

$m(_{20}^{40}\textrm{Ca})=39.962591\; u$

$m(_{20}^{41}\textrm{Ca})=40.962278 \; u$

$m(_{13}^{26}\textrm{Al})=25.986895 \; u$

$m(_{13}^{27}\textrm{Al})=26.981541 \; u$

Answer:

The reaction showing the neutron separation is

$_{13}^{27}\textrm{Al}+E\rightarrow _{13}^{26}\textrm{Al}+_{0}^{1}\textrm{n}$

$\\E=(m(_{13}^{26}\textrm{Ca})+m(_{0}^{1}\textrm{n})-m(_{13}^{27}\textrm{Ca}))c^{2}\\ $

$\\E=(25.986895+1.008665-26.981541)c^{2} \\$
$\\E=(0.014019)u\times c^{2}$

But 1u=931.5 MeV/$c^{2}$

Therefore E=(0.014019) $\times$ 931.5

E=13.059 MeV

Therefore to remove a neutron from the $_{13}^{27}\textrm{Al}$ nucleus 13.059 MeV of energy is required

15. A source contains two phosphorous radio nuclides $_{15}^{32}\textrm{P}(T_{1/2}=14.3d)$ and $_{15}^{33}\textrm{P}(T_{1/2}=25.3d)$ . Initially, 10% of the decays come from $_{15}^{33}\textrm{P}$ . How long one must wait until 90% do so?

Answer:

Let initially there be $\mathrm{N}_1$ atoms of ${ }_{15}^{32} \mathrm{P}$ and $\mathrm{N}_2$ atoms of ${ }_{15}^{33} \mathrm{P}$ and let their decay constants be $\lambda_1$ and $\lambda_2$ respectively Since initially the activity of ${ }_{15}^{33} \mathrm{P}$ is $1 / 9$ times that of ${ }_{15}^{32} \mathrm{P}$ we have

$
N_1 \lambda_1=\frac{N_2 \lambda_2}{9}
$

Let after time $t$ the activity of ${ }_{15}^{33} \mathrm{P}$ be 9 times that of ${ }_{15}^{32} \mathrm{P}$

$
N_1 \lambda_1 e^{-\lambda_1 t}=9 N_2 \lambda_2 e^{-\lambda_2 t}
$

Dividing equation (ii) by (i) and taking the natural $\log$ of both sides we get

$
\begin{aligned}
& -\lambda_1 t=\ln 81-\lambda_2 t \\
& t=\frac{\ln 81}{\lambda_2-\lambda_1}
\end{aligned}
$

where $\lambda_2=0.048 /$ day and $\lambda_1=0.027 /$ day
t comes out to be 208.5 days

16. Under certain circumstances, a nucleus can decay by emitting a particle more massive than an $\alpha$ -particle. Consider the following decay processes:

$_{88}^{223}\textrm{Ra}\rightarrow _{82}^{209}\textrm{Pb}+_{6}^{14}\textrm{C}$

$_{88}^{223}\textrm{Ra}\rightarrow _{86}^{219}\textrm{Rn}+_{2}^{4}\textrm{He}$

Calculate the Q-values for these decays and determine that both are energetically allowed.

Answer:

$_{88}^{223}\textrm{Ra}\rightarrow _{82}^{209}\textrm{Pb}+_{6}^{14}\textrm{C}$

$\\\Delta m=m(_{88}^{223}\textrm{Ra})-m(_{82}^{209}\textrm{Pb})-m(_{6}^{14}\textrm{C})\\ =223.01850-208.98107-14.00324 \\=0.03419u$

1 u = 931.5 MeV/$c^{2}$

Q=0.03419 $\times$ 931.5

=31.848 MeV

As the Q value is positive the reaction is energetically allowed

$_{88}^{223}\textrm{Ra}\rightarrow _{86}^{219}\textrm{Rn}+_{2}^{4}\textrm{He}$

$\\\Delta m=m(_{88}^{223}\textrm{Ra})-m(_{86}^{219}\textrm{Rn})-m(_{2}^{4}\textrm{He})\\ =223.01850-219.00948-4.00260 \\=0.00642u$

1 u = 931.5 MeV/$c^{2}$

Q=0.00642 $\times$ 931.5

=5.98 MeV

As the Q value is positive, the reaction is energetically allowed

17. Consider the fission of $_{92}^{238}\textrm{U}$ by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are $_{58}^{140}\textrm{Ce}$ and $_{44}^{99}\textrm{Ru}$ . Calculate Q for this fission process. The relevant atomic and particle masses are

$m(_{92}^{238}\textrm{U})=238.05079\; u$

$m(_{58}^{140}\textrm{Ce})=139.90543\; u$

$m(_{44}^{99}\textrm{Ru})= 98.90594\; u$

Answer:

The fission reaction given in the question can be written as

$_{92}^{238}\textrm{U}+_{0}^{1}\textrm{n}\rightarrow _{58}^{140}\textrm{Ce}+_{44}^{99}\textrm{Ru}+10e^{-}$

The mass defect for the above reaction would be

$\Delta m=m_{N}(_{92}^{238}\textrm{U})+m(_{0}^{1}\textrm{n})-m_{N}(_{58}^{140}\textrm{Ce})-m_{N}(_{44}^{99}\textrm{Ce})-10m_{e}$

In the above equation, m_N represents nuclear masses

$\\\Delta m=m(_{92}^{238}\textrm{U})-92m_{e}+m(_{0}^{1}\textrm{n})-m(_{58}^{140}\textrm{Ce})+58m_{e}-m(_{44}^{99}\textrm{Ru})+44m_{e}-10m_{e} \\\Delta m=m(_{92}^{238}\textrm{U})+m(_{0}^{1}\textrm{n})-m(_{58}^{140}\textrm{Ce})-m(_{44}^{99}\textrm{Ru})\\ \Delta m=238.05079+1.008665-139.90543-98.90594\\ \Delta m=0.247995u$

but 1u =931.5 MeV/$c^{2}$

Q=0.247995 $\times$ 931.5

Q=231.007 MeV

Q value of the fission process is 231.007 MeV

18. (a)Consider the D–T reaction (deuterium-tritium fusion)

$_{1}^{2}\textrm{H}+_{1}^{3}\textrm{H}\rightarrow _{2}^{4}\textrm{He}+n$ Calculate the energy released in MeV in this reaction from the data:

$m(_{1}^{2}\textrm{H})=2.014102\; u$

$m(_{1}^{3}\textrm{H})=3.016049\; u$

Answer:

The mass defect of the reaction is

$\\\Delta m=m(_{1}^{2}\textrm{H})+m(_{1}^{3}\textrm{H})-m(_{2}^{4}\textrm{He})-m(_{0}^{1}\textrm{n})\\ $
$\Delta m=2.014102+3.016049-4.002603-1.008665\\ $
$\Delta m=0.018883u$

1u = 931.5 MeV/$c^{2}$

Q=0.018883 $\times$ 931.5=17.59 MeV

18. (b) Consider the D–T reaction (deuterium-tritium fusion)

$_{1}^{2}\textrm{H}+_{1}^{3}\textrm{H}\rightarrow _{2}^{4}\textrm{He}+n$

Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles $= 2(3kT/2)$ ; k = Boltzmann’s constant, T = absolute temperature.)

Answer:

To initiate the reaction, both the nuclei would have to come in contact with each other.

Just before the reaction, the distance between their centres would be 4.0 fm.

The electrostatic potential energy of the system at that point would be

$\\U=\frac{q^{2}}{4\pi \epsilon _{0}d}\\ $
$U=\frac{9\times 10^{9}(1.6\times 10^{-19})^{2}}{4\times 10^{-15}}\\$
$U=5.76\times 10^{-14}J$

The same amount of Kinetic Energy K, would be required to overcome the electrostatic forces of repulsion to initiate the reaction

It is given that $K=2\times \frac{3kT}{2}$

Therefor,e the temperature required to initiate the reaction is

$\\T=\frac{K}{3k}\\ =\frac{5.76\times 10^{-14}}{3\times 1.38\times 10^{-23}}\\=1.39\times 10^{9}\ K$

19. Obtain the maximum kinetic energy of $\beta$ - particles, and the radiation frequencies of $\gamma$ decays in the decay scheme shown in Fig. You are given that

$m(^{198}Au)=197.968233\; u$

$m(^{198}Hg)=197.966760 \; u$

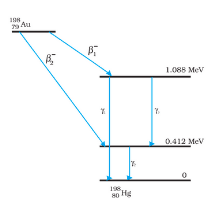
Answer:

$\gamma _{1}$ decays from 1.088 MeV to 0 V

Frequency of $\gamma _{1}$ is

$\\\nu _{1}=\frac{1.088\times 10^{6}\times 1.6\times 10^{-19}}{6.62\times 10^{-34}}\\ $
$\nu _{1}=2.637\times 10^{20}\ Hz$

Planck's constant, h=6.62 $\times$ $10 ^{-34}$ Js,

$E=h\nu$

Similarly, we can calculate frequencies of $\gamma _{2}$ and $\gamma _{3}$

$\\\nu _{2}=9.988\times 10^{19}\ Hz\\ $
$\nu _{3}=1.639\times 10^{20}\ Hz$

The energy of the highest level would be equal to the energy released after the decay

Mass defect is

$\\\Delta m=m(_{79}^{196}\textrm{U})-m(_{80}^{196}\textrm{Hg})\\ $
$\Delta m=197.968233-197.966760\\$
$\Delta m=0.001473u$

We know 1u = 931.5 MeV/$c^{2}$

Q value= 0.001473 $\times$ 931.5=1.3721 MeV

The maximum Kinetic energy of $\beta _{1}^{-}$ would be 1.3721-1.088=0.2841 MeV

The maximum Kinetic energy of $\beta _{2}^{-}$ would be 1.3721-0.412=0.9601 MeV

20. Calculate and compare the energy released by a) fusion of 1.0 kg of hydrogen deep within Sun and b) the fission of 1.0 kg of 235U in a fission reactor.

Answer:

(a) ${ }_1^1 \mathrm{H}_1^1 \mathrm{H}+{ }_1^1 \mathrm{H}+{ }_1^1 \mathrm{H}+{ }_1^1 \mathrm{H} \rightarrow{ }_2^4 \mathrm{He}$

The above fusion reaction releases the energy of 26 MeV
Number of Hydrogen atoms in 1.0 kg of Hydrogen is $1000 \mathrm{~N}_{\mathrm{A}}$
Therefore $250 \mathrm{~N}_{\mathrm{A}}$ such reactions would take place
The energy released in the whole process is $\mathrm{E}_1$

$
\begin{aligned}
& =250 \times 6.023 \times 10^{23} \times 26 \times 10^6 \times 1.6 \times 10^{-19} \\
& =6.2639 \times 10^{14} J
\end{aligned}
$

(b) The energy released in fission of one ${ }_{92}^{235} \mathrm{U}$ atom is 200 MeV

Number of ${ }_{92}^{235} \mathrm{U}$ atoms present in 1 kg of ${ }_{92}^{235} \mathrm{U}$ is N

$
\begin{aligned}
& N=\frac{1000 \times 6.023 \times 10^{23}}{235} \\
& N=2.562 \times 10^{24}
\end{aligned}
$

The energy released on fission of N atoms is $\mathrm{E}_2$

$
\begin{aligned}
& E=2.562 \times 10^{24} \times 200 \times 10^6 \times 1.6 \times 10^{-19} \\
& E=8.198 \times 10^{13} J \\
& \frac{E_1}{E_2}=\frac{6.2639 \times 10^{14}}{8.198 \times 10^{13}} \approx 8
\end{aligned}
$