• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Miscellaneous Exercise Chapter 5 Class 12 - Continuity and Differentiability

NCERT Solutions for Miscellaneous Exercise Chapter 5 Class 12 - Continuity and Differentiability

Edited By Ramraj Saini | Updated on Dec 04, 2023 12:20 PM IST | #CBSE Class 12th
Upcoming Event
CBSE Class 12th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 12 Chapter 5 Miscellaneous Exercise

NCERT Solutions for miscellaneous exercise chapter 5 class 12 Continuity and Differentiability are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. In the Class 12 Maths chapter 5 miscellaneous exercise solutions, you will get a mixture of questions from all the previous exercises of this Class 12 Maths NCERT textbook chapter. You will get questions related to first-order derivatives of different types of functions, second-order derivatives, mean-value theorem, Rolle's theorem in the miscellaneous exercise chapter 5 Class 12. This Class 12 NCERT syllabus exercise is a bit difficult as compared to previous exercises, so you may not be able to solve NCERT problems from this exercise at first.

You can take help from NCERT solutions for Class 12 Maths chapter 5 miscellaneous exercise to get clarity. There are not many questions asked in the board exams from this exercise, but Class 12 Maths chapter 5 miscellaneous solutions are important for the students who are preparing for competitive exams like JEE main, SRMJEE, VITEEE, MET, etc. Miscellaneous exercise class 12 chapter 5 are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise enumerated in NCERT Book together using the link provided below.

Also, see

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Access NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise

Download PDF

Continuity and Differentiability Miscellaneous Exercise:

Question:1 Differentiate w.r.t. x the function in Exercises 1 to 11.

( 3x^2 - 9x + 5 )^9

Answer:

Given function is
f(x)=( 3x^2 - 9x + 5 )^9
Now, differentiation w.r.t. x is
f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d((3x^2-9x+5)^9)}{dx}= 9(3x^2-9x+5)^8.(6x-9)
= 27(2x-3)(3x^2-9x+5)^8
Therefore, differentiation w.r.t. x is 27(3x^2-9x+5)^8(2x-3)

Question:2 Differentiate w.r.t. x the function in Exercises 1 to 11.

\sin ^3 x + \cos ^6 x

Answer:

Given function is
f(x)= \sin ^3 x + \cos ^6 x
Now, differentiation w.r.t. x is
f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\sin^3x +\cos^6x)}{dx}=3\sin^2x.\frac{d(\sin x)}{dx}+6\cos^5x.\frac{d(\cos x)}{dx}
=3\sin^2x.\cos x+6\cos^5x.(-\sin x)
=3\sin^2x\cos x- 6\cos^5x\sin x = 3\sin x\cos x(\sin x- 2\cos ^4x)

Therefore, differentiation w.r.t. x is 3\sin x\cos x(\sin x- 2\cos ^4x)

Question:3 Differentiate w.r.t. x the function in Exercises 1 to 11.

( 5 x) ^{ 3 \cos 2x }

Answer:

Given function is
y=( 5 x) ^{ 3 \cos 2x }
Take, log on both the sides
\log y = 3\cos 2x\log 5x
Now, differentiation w.r.t. x is
By using product rule
\frac{1}{y}.\frac{dy}{dx} = 3.(-2\sin 2x)\log 5x + 3\cos 2x.\frac{1}{5x}.5= -6\sin2x\log 5x +\frac{3\cos 2x}{x}\\ \frac{dy}{dx} = y.\left ( -6\sin2x\log 5x +\frac{3\cos 2x}{x} \right )\\ \frac{dy}{dx} = (5x)^{3\cos 2x}.\left ( -6\sin2x\log 5x +\frac{3\cos 2x}{x} \right )

Therefore, differentiation w.r.t. x is (5x)^{3\cos 2x}.\left ( \frac{3\cos 2x}{x}-6\sin2x\log 5x \right )

Question:4 Differentiate w.r.t. x the function in Exercises 1 to 11.

\sin ^ {-1} (x \sqrt x ) , 0 \leq x\leq 1

Answer:

Given function is
f(x)=\sin ^ {-1} (x \sqrt x ) , 0 \leq x\leq 1
Now, differentiation w.r.t. x is
f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\sin^{-1}x\sqrt x)}{dx}=\frac{1}{\sqrt{1-(x\sqrt x)^2}}.\frac{d(x\sqrt x)}{dx}
=\frac{1}{\sqrt{1-x^3}}.\left ( 1.\sqrt x+x\frac{1}{2\sqrt x} \right )
=\frac{1}{\sqrt{1-x^3}}.\left ( \frac{3\sqrt x}{2} \right )
=\frac{3}{2}.\sqrt{\frac{x}{1-x^3}}

Therefore, differentiation w.r.t. x is \frac{3}{2}.\sqrt{\frac{x}{1-x^3}}

Question:5 Differentiate w.r.t. x the function in Exercises 1 to 11.

\frac{\cos ^{-1}x/2}{\sqrt {2x+7}} , -2 < x < 2

Answer:

Given function is
f(x)=\frac{\cos ^{-1}x/2}{\sqrt {2x+7}} , -2 < x < 2
Now, differentiation w.r.t. x is
By using the Quotient rule
f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\frac{\cos^{-1}\frac{x}{2}}{\sqrt{2x+7}})}{dx}=\frac{\frac{d(\cos^{-1}\frac{x}{2})}{dx}.\sqrt{2x+7}-\cos^{-1}\frac{x}{2}.\frac{d(\sqrt{2x+7})}{dx}}{(\sqrt{2x+7})^2}\\ f^{'}(x) = \frac{\frac{-1}{\sqrt{1-(\frac{x}{2})^2}}.\frac{1}{2}.\sqrt{2x+7}-\cos^{-1}\frac{x}{2}.\frac{1}{2.\sqrt{2x+7}}.2}{2x+7}\\ f^{'}(x)= -\left [\frac{1}{(\sqrt{4-x^2})(\sqrt{2x+7})}+\frac{\cos^{-1}\frac{x}{2}}{(2x+7)^\frac{3}{2}} \right ]

Therefore, differentiation w.r.t. x is -\left [\frac{1}{(\sqrt{4-x^2})(\sqrt{2x+7})}+\frac{\cos^{-1}\frac{x}{2}}{(2x+7)^\frac{3}{2}} \right ]

Question:6 Differentiate w.r.t. x the function in Exercises 1 to 11.

\cot ^{-1} \left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} \right ] , 0 < x < \pi /2

Answer:

Given function is
f(x)=\cot ^{-1} \left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} \right ] , 0 < x < \pi /2
Now, rationalize the [] part
\left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} \right ]= \left [ \frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt {1+ \sin x }- \sqrt {1- \sin x }} .\frac{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}{\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x }}\right ]

=\frac{(\sqrt { 1+ \sin x }+ \sqrt { 1- \sin x })^2}{(\sqrt{1+\sin x})^2-(\sqrt{1-\sin x})^2} \ \ \ \ \ \ (Using \ (a-b)(a+b)=a^2-b^2)

=\frac{((\sqrt { 1+ \sin x })^2+ (\sqrt { 1- \sin x })^2+2(\sqrt { 1+ \sin x })(\sqrt { 1- \sin x }))}{1+\sin x-1+\sin x}
(Using \ (a+b)^2=a^2+b^2+2ab)
=\frac{1+\sin x+1-\sin x+2\sqrt{1-\sin^2x} }{2\sin x}

=\frac{2(1+\cos x)}{2\sin x} = \frac{1+\cos x}{\sin x}

=\frac{2\cos^2\frac{x}{2}}{2\sin\frac{x}{2}\cos\frac{x}{2}} \ \ \ \ \ (\because 2\cos^2= 1+\cos2x \ and \ \sin2x = 2\sin x\cos x)

=\frac{2\cos\frac{x}{2}}{2\sin\frac{x}{2}} = \cot \frac{x}{2}
Given function reduces to
f(x) = \cot^{-1}(\cot \frac{x}{2})\\ f(x) = \frac{x}{2}
Now, differentiation w.r.t. x is
f^{'}(x)=\frac{d(f(x))}{dx}=\frac{d(\frac{x}{2})}{dx} = \frac{1}{2}
Therefore, differentiation w.r.t. x is \frac{1}{2}

Question:7 Differentiate w.r.t. x the function in Exercises 1 to 11. ( \log x )^{ \log x } , x > 1

Answer:

Given function is
y=( \log x )^{ \log x } , x > 1
Take log on both sides
\log y=\log x\log( \log x )
Now, differentiate w.r.t.
\frac{1}{y}.\frac{dy}{dx}= \frac{1}{x}.\log (\log x)+\log x.\frac{1}{\log x}.\frac{1}{x} = \frac{\log x+1}{x}
\frac{dy}{dx} = y.\left ( \frac{\log x+1}{x} \right )\\
\frac{dy}{dx} = (\log x)^{\log x}.\left ( \frac{\log x+1}{x} \right )\\
Therefore, differentiation w.r.t x is (\log x)^{\log x}.\left ( \frac{\log x+1}{x} \right )\\

Question:8 \cos ( a \cos x + b \sin x ), for some constant a and b.

Answer:

Given function is
f(x)=\cos ( a \cos x + b \sin x )
Now, differentiation w.r.t x
f^{'}(x)= \frac{d(f(x))}{dx}= \frac{d(\cos(a\cos x+ b \sin x))}{dx}
= -\sin(a\cos x+b\sin x).\frac{d(a\cos x+b\sin x)}{dx}
= -\sin(a\cos x+b\sin x).(-a\sin x+b\cos x)
= (a\sin x-b\cos x)\sin(a\cos x+b\sin x).
Therefore, differentiation w.r.t x (a\sin x-b\cos x)\sin(a\cos x+b\sin x)

Question:9 (\sin x - \cos x)^{ (\sin x - \cos x), } , \frac{\pi }{4} <x<\frac{3 \pi }{4}

Answer:

Given function is
y=(\sin x - \cos x)^{ (\sin x - \cos x), } , \frac{\pi }{4} <x<\frac{3 \pi }{4}
Take log on both the sides
\log y=(\sin x - \cos x)\log (\sin x - \cos x)
Now, differentiate w.r.t. x
\frac{1}{y}.\frac{dy}{dx} = \frac{d(\sin x-\cos x)}{dx}.\log(\sin x- \cos x)+(\sin x- \cos x).\frac{d(\log(\sin x- \cos x))}{dx}
\frac{1}{y}.\frac{dy}{dx} =(\cos x -(-\sin x)).\log(\sin x-\cos x)+(\sin x- \cos x).\frac{(\cos x -(-\sin x))}{(\sin x- \cos x)}
\frac{dy}{dx} =y.(\cos x +\sin x)\left ( \log(\sin x-\cos x)+1 \right )
\frac{dy}{dx} =(\sin x-\cos x)^{(\sin x-\cos x)}.(\cos x +\sin x)\left ( \log(\sin x-\cos x)+1 \right )
Therefore, differentiation w.r.t x is (\sin x-\cos x)^{(\sin x-\cos x)}.(\cos x +\sin x)\left ( \log(\sin x-\cos x)+1 \right ), sinx>cosx

Question:10x ^x + x ^a + a ^x + a ^a , for some fixed a > 0 and x > 0

Answer:

Given function is
f(x)=x ^x + x ^a + a ^x + a ^a
Lets take
u = x^x
Now, take log on both sides
\log u = x \log x
Now, differentiate w.r.t x
\frac{1}{u}.\frac{du}{dx}= \frac{dx}{dx}.\log x+x.\frac{d(\log x)}{dx}\\ \\ \frac{1}{u}.\frac{du}{dx}= 1.\log x+x.\frac{1}{x}\\ \\ \frac{du}{dx}= y.(\log x+1)\\ \\ \frac{du}{dx}= x^x.(\log x+1) -(i)
Similarly, take v = x^a
take log on both the sides
\log v = a\log x
Now, differentiate w.r.t x
\frac{1}{v}.\frac{dv}{dx}= a.\frac{d(\log x)}{dx}=a.\frac{1}{x}= \frac{a}{x}\\ \\ \frac{dv}{dx}= v.\frac{a}{x}\\ \\ \frac{dv}{dx}= x^a.\frac{a}{x} -(ii)

Similarly, take z = a^x
take log on both the sides
\log z = x\log a
Now, differentiate w.r.t x
\frac{1}{z}.\frac{dz}{dx}=\log a.\frac{d(x)}{dx}=\log a.1= \log a\\ \\ \frac{dz}{dx}= z.\log a\\ \\ \frac{dz}{dx}= a^x.\log a -(iii)

Similarly, take w = a^a
take log on both the sides
\log w = a\log a= \ constant
Now, differentiate w.r.t x
\frac{1}{w}.\frac{dw}{dx}= a.\frac{d(a\log a)}{dx}= 0\\ \\ \frac{dw}{dx} = 0 -(iv)
Now,
f(x)=u+v+z+w
f^{'}(x) = \frac{du}{dx}+\frac{dv}{dx}+\frac{dz}{dx}+\frac{dw}{dx}
Put values from equation (i) , (ii) ,(iii) and (iv)
f^{'}(x)= x^x(\log x+1)+ax^{a-1}+a^x\log a
Therefore, differentiation w.r.t. x is x^x(\log x+1)+ax^{a-1}+a^x\log a

Question:11x ^{x^2 -3} + ( x-3 ) ^{x^2} , for\: \: x > 3

Answer:

Given function is
f(x)=x ^{x^2 -3} + ( x-3 ) ^{x^2} , for\: \: x > 3
take u=x ^{x^2 -3}
Now, take log on both the sides
\log u=(x^2-3)\log x
Now, differentiate w.r.t x
\frac{1}{u}.\frac{du}{dx}= \frac{d(x^2-3)}{dx}.\log x+(x^2-3).\frac{d(\log x)}{dx}\\ \\ \frac{1}{u}.\frac{du}{dx} = 2x.\log x+(x^2-3).\frac{1}{x}\\ \\ \frac{1}{u}.\frac{du}{dx} = \frac{2x^2\log x+x^2-3}{x}\\ \\ \frac{du}{dx}= u.\left ( \frac{2x^2\log x+x^2-3}{x} \right )\\ \\ \frac{du}{dx}= x^{(x^2-3)}.\left ( \frac{2x^2\log x+x^2-3}{x} \right )\\ \\ -(i)
Similarly,
take v=(x-3)^x^2\\
Now, take log on both the sides
\log v=x^2\log (x-3)
Now, differentiate w.r.t x
\frac{1}{v}.\frac{dv}{dx}= \frac{d(x^2)}{dx}.\log (x-3)+x^2.\frac{d(\log (x-3))}{dx}\\ \\ \frac{1}{v}.\frac{dv}{dx} = 2x.\log (x-3)+x^2.\frac{1}{(x-3)}\\ \\ \frac{1}{v}.\frac{dv}{dx} = 2x\log(x-3)+\frac{x^2}{x-3}\\ \\ \frac{dv}{dx}= v.\left ( 2x\log(x-3)+\frac{x^2}{x-3} \right )\\ \\ \frac{dv}{dx}= (x-3)^{x^2}.\left ( 2x\log(x-3)+\frac{x^2}{x-3}\right )\\ \\ -(ii)
Now
f(x)= u + v
f^{'}(x)= \frac{du}{dx}+\frac{dv}{dx}
Put the value from equation (i) and (ii)
f^{'}(x)= x^{(x^2-3)}.\left ( \frac{2x^2\log x+x^2-3}{x} \right )+(x-3)^{x^2}.\left ( 2x\log(x-3)+\frac{x^2}{x-3}\right )
Therefore, differentiation w.r.t x is x^{(x^2-3)}.\left ( \frac{2x^2\log x+x^2-3}{x} \right )+(x-3)^{x^2}.\left ( 2x\log(x-3)+\frac{x^2}{x-3}\right )

Question:12 Find dy/dx if y = 12 (1 - \cos t), x = 10 (t - \sin t), -\frac{\pi }{2} <t< \frac{\pi }{2}

Answer:

Given equations are
y = 12 (1 - \cos t), x = 10 (t - \sin t),
Now, differentiate both y and x w.r.t t independently
\frac{dy}{dt}=\frac{d(12(1-\cos t))}{dt}= -12(-\sin t)=12\sin t
And
\frac{dx}{dt}=\frac{d(10(t-\sin t))}{dt}= 10-10\cos t
Now
\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}= \frac{12\sin t}{10(1-\cos t)} = \frac{6}{5}.\frac{2\sin \frac{t}{2}\cos \frac{t}{2}}{2\sin^2\frac{t}{2}} = \frac{6}{5}.\frac{\cos \frac{t}{2}}{\sin \frac{t}{2}}\\ \\
(\because \sin 2x = 2\sin x\cos x \ and \ 1-\cos 2x = 2\sin^2x)
\frac{dy}{dx}=\frac{6}{5}.\cot \frac{t}{2}
Therefore, differentiation w.r.t x is \frac{6}{5}.\cot \frac{t}{2}

Question:13 Find dy/dx if y = sin ^{-1} x + sin^{-1} \sqrt{1- x^2} , 0 <x< 1

Answer:

Given function is
y = sin ^{-1} x + sin^{-1} \sqrt{1- x^2} , 0 <x< 1
Now, differentiatiate w.r.t. x
\frac{dy}{dx}= \frac{d(sin ^{-1} x + sin^{-1} \sqrt{1- x^2})}{dx} = \frac{1}{\sqrt{1-x^2}}+\frac{1}{\sqrt{1-(\sqrt{1-x^2})^2}}.\frac{d(\sqrt{1-x^2})}{dx}\\ \frac{dy}{dx}= \frac{1}{\sqrt{1-x^2}}+\frac{1}{\sqrt{1-1+x^2}}.\frac{1}{2\sqrt{1-x^2}}.(-2x)\\ \\ \frac{dy}{dx}= \frac{1}{\sqrt{1-x^2}}-\frac{1}{\sqrt{1-x^2}}\\ \frac{dy}{dx}= 0
Therefore, differentiatiate w.r.t. x is 0

Question:14 If x \sqrt {1+ y }+ y \sqrt { 1+ x } = 0 \: \: for \: \: , -1 < x < 1 \: \:prove \: \: that \: \frac{dy}{dx} = -\frac{1}{(1+x)^2}

Answer:

Given function is
x \sqrt {1+ y }+ y \sqrt { 1+ x } = 0
x\sqrt{1+y} = - y\sqrt{1+x}
Now, squaring both sides
(x\sqrt{1+y})^2 = (- y\sqrt{1+x})^2\\ x^2(1+y)=y^2(1+x)\\ x^2+x^2y=y^2x+y^2\\ x^2-y^2=y^2x-x^2y\\ (x-y)(x+y) = -xy(x-y) \\ x+y =-xy\\ y = \frac{-x}{1+x}
Now, differentiate w.r.t. x is
\frac{dy}{dx} = \frac{d(\frac{-x}{1+x})}{dx}= \frac{-1.(1+x)-(-x).(1)}{(1+x)^2}= \frac{-1}{(1+x)^2}
Hence proved

Question:15 If (x - a)^2 + (y - b)^2 = c^2 , for some c > 0, prove that\frac{\left [ 1+(\frac{dy}{dx} )^2 \right ]^{3/2}}{\frac{d^2 y }{dx^2}}\: is a constant independent of a and b.

Answer:

Given function is
(x - a)^2 + (y - b)^2 = c^2
(y - b)^2 = c^2-(x - a)^2 - (i)
Now, differentiate w.r.t. x
\frac{d((x-a)^2)}{dx}+\frac{((y-b)^2)}{dx}=\frac{d(c^2)}{dx}\\ \\ 2(x-a)+2(y-b).\frac{dy}{dx}=0\\ \\ \frac{dy}{dx} = \frac{a-x}{y-b} -(ii)
Now, the second derivative
\frac{d^2y}{dx^2} = \frac{\frac{d(a-x)}{dx}.(y-b) -(a-x).\frac{d(y-b)}{dx}}{(y-b)^2}\\ \\ \frac{d^2y}{dx^2} =\frac{ (-1).(y-b)-(a-x).\frac{dy}{dx}}{(y-b)^2}\\ \\
Now, put values from equation (i) and (ii)
\frac{d^2y}{dx^2} =\frac{-(y-b)-(a-x).\frac{a-x}{y-b}}{(y-b)^2}\\ \\ \frac{d^2y}{dx^2} = \frac{-((y-b)^2+(a-x)^2)}{(y-b)^\frac{3}{2}} = \frac{-c^2}{(y-b)^\frac{3}{2}} (\because (x - a)^2 + (y - b)^2 = c^2)
Now,
\frac{\left [ 1+(\frac{dy}{dx} )^2 \right ]^{3/2}}{\frac{d^2 y }{dx^2}} = \frac{\left ( 1+\left ( \frac{x-a}{y-b} \right )^2 \right )^\frac{3}{2}}{\frac{-c^2}{(y-b)^\frac{3}{2}}} = \frac{\frac{\left ( (y-b)^2 +(x-a)^2\right )^\frac{3}{2}}{(y-b)^\frac{3}{2}}}{\frac{-c^2}{(y-b)^\frac{3}{2}}} = \frac{(c^2)^\frac{3}{2}}{-c^2}= \frac{c^3}{-c^2}= c (\because (x - a)^2 + (y - b)^2 = c^2)
Which is independent of a and b
Hence proved

Question:16 If \cos y = x \cos (a + y), with \cos a \neq \pm 1 , prove that \frac{dy}{dx} = \frac{\cos ^2 (a+y )}{\sin a }

Answer:

Given function is
\cos y = x \cos (a + y)
Now, Differentiate w.r.t x
\frac{d(\cos y)}{dx} = \frac{dx}{dx}.\cos(a+y)+x.\frac{d(\cos (a+y))}{dx}\\ \\ -\sin y \frac{dy}{dx} = 1.\cos (a+y)+x.(-\sin(a+y)).\frac{dy}{dx}\\ \\ \frac{dy}{dx}.(x\sin(a+y)-\sin y)= \cos(a+y)\\ \\ \frac{dy}{dx}.(\frac{\cos y}{\cos (a+b)}.\sin(a+y)-\sin y)= \cos(a+b) \ \ \ \ \ (\because x = \frac{\cos y}{\cos (a+b)})\\ \\ \frac{dy}{dx}.(\cos y\sin(a+y)-\sin y\cos(a+y))=\cos^2(a+b)\\ \\ \frac{dy}{dx}.(\sin(a+y-y))=\cos^2(a+b) \ \ \ \ \ \ \ (\because \cos A\sin B-\sin A\cos B = \sin(A-B))\\ \\ \frac{dy}{dx}= \frac{\cos^2(a+y)}{\sin a}
Hence proved

Question:17 If x = a (\cos t + t \sin t) and y = a (\sin t - t \cos t), find \frac{d^2 y }{dx^2 }

Answer:

Given functions are
x = a (\cos t + t \sin t) and y = a (\sin t - t \cos t)
Now, differentiate both the functions w.r.t. t independently
We get
\frac{dx}{dt} = \frac{d(a(\cos t +t\sin t))}{dt}= a(-\sin t)+a(\sin t+t\cos t)
=-a\sin t+a\sin t+at\cos t = at\cos t
Similarly,
\frac{dy}{dt} = \frac{d(a(\sin t - t\cos t))}{dt}= a\cos t -a(\cos t+t(-\sin t))
= a\cos t -a\cos t+at\sin t =at\sin t
Now,
\frac{dy}{dx}= \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{at\sin t}{at \cos t} = \tan t
Now, the second derivative
\frac{d^2y}{dx^2}=\frac{d}{dx}\frac{dy}{dx}= \sec^2 t.\frac{dt}{dx}=\frac{\sec^2t.\sec t }{at}=\frac{\sec^3t}{at}
(\because \frac{dx}{dt} = at\cos t \Rightarrow \frac{dt}{dx}= \frac{1}{at\cos t}=\frac{\sec t}{at})
Therefore, \frac{d^2y}{dx^2}=\frac{\sec^3t}{at}

Question:18 Iff (x) = |x|^3, show that f ''(x) exists for all real x and find it.

Answer:

Given function is
f (x) = |x|^3
f(x)\left\{\begin{matrix} -x^3 & x<0\\ x^3 & x>0 \end{matrix}\right.
Now, differentiate in both the cases
f(x)= x^3\\ f^{'}(x)=3x^2\\ f^{''}(x)= 6x
And
f(x)= -x^3\\ f^{'}(x)=-3x^2\\ f^{''}(x)= -6x
In both, the cases f ''(x) exist
Hence, we can say that f ''(x) exists for all real x
and values are
f^{''}(x)\left\{\begin{matrix} -6x &x<0 \\ 6x& x>0 \end{matrix}\right.

Question:19 Using mathematical induction prove that \frac{d}{dx} (x^n) = nx ^{n-1} for all positive integers n.

Answer:

Given equation is
\frac{d}{dx} (x^n) = nx ^{n-1}
We need to show that \frac{d}{dx} (x^n) = nx ^{n-1} for all positive integers n
Now,
For ( n = 1) \Rightarrow \frac{d(x^{1})}{dx}= 1.x^{1-1}= 1.x^0=1
Hence, true for n = 1
For (n = k) \Rightarrow \frac{d(x^{k})}{dx}= k.x^{k-1}
Hence, true for n = k
For ( n = k+1) \Rightarrow \frac{d(x^{k+1})}{dx}= \frac{d(x.x^k)}{dx}
= \frac{d(x)}{dx}.x^k+x.\frac{d(x^k)}{dx}
= 1.x^k+x.(k.x^{k-1}) = x^k+k.x^k= (k+1)x^k
Hence, (n = k+1) is true whenever (n = k) is true
Therefore, by the principle of mathematical induction we can say that \frac{d}{dx} (x^n) = nx ^{n-1} is true for all positive integers n

Question:20 Using the fact that \sin (A + B) = \sin A \cos B + \cos A \sin B and the differentiation,
obtain the sum formula for cosines.

Answer:

Given function is
\sin (A + B) = \sin A \cos B + \cos A \sin B
Now, differentiate w.r.t. x
\frac{d(\sin(A+B))}{dx} = \frac{d\sin A}{dx}.\cos B+\sin A.\frac{d\cos B}{dx}+\frac{d\cos A}{dx}.\sin B+\cos A.\frac{d\sin B}{dx}
\cos (A+b)\frac{d(A+B)}{dx} =\frac{dA}{dx}(\cos A\cos B-\sin A\cos B)+\frac{dB}{dx}(\cos A \sin B-\sin A\sin B)
=(\cos A \sin B-\sin A\sin B).\frac{d(A+B)}{dx}
\cos(A+B)= \cos A\sin B-\sin A\cos B
Hence, we get the formula by differentiation of sin(A + B)

Question:21 Does there exist a function which is continuous everywhere but not differentiable
at exactly two points? Justify your answer.

Answer:

Consider f(x) = |x| + |x +1|
We know that modulus functions are continuous everywhere and sum of two continuous function is also a continuous function
Therefore, our function f(x) is continuous
Now,
If Lets differentiability of our function at x = 0 and x= -1
L.H.D. at x = 0
\lim_{h\rightarrow 0^-}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^-}\frac{f(h)-f(0)}{h}= \lim_{h\rightarrow 0^-}\frac{|h|+|h+1|-|1|}{h}
=\lim_{h\rightarrow 0^-}\frac{-h-(h+1)-1}{h}= 0 (|h| = - h \ because\ h < 0)
R.H.L. at x = 0
\lim_{h\rightarrow 0^+}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^+}\frac{f(h)-f(0)}{h}= \lim_{h\rightarrow 0^+}\frac{|h|+|h+1|-|1|}{h}
=\lim_{h\rightarrow 0^+}\frac{h+h+1-1}{h}= \lim_{h\rightarrow 0^+}\frac{2h}{h}= 2 (|h| = h \ because \ h > 0)
R.H.L. is not equal to L.H.L.
Hence.at x = 0 is the function is not differentiable
Now, Similarly
R.H.L. at x = -1
\lim_{h\rightarrow 0^+}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^+}\frac{f(-1+h)-f(-1)}{h}= \lim_{h\rightarrow 0^+}\frac{|-1+h|+|h|-|-1|}{h}
=\lim_{h\rightarrow 0^+}\frac{1-h+h-1}{h}= \lim_{h\rightarrow 0^+}\frac{0}{h}= 0 (|h| = h \ because \ h > 0)
L.H.L. at x = -1
\lim_{h\rightarrow 0^-}\frac{f(x+h)-f(x)}{h}= \lim_{h\rightarrow 0^-}\frac{f(1+h)-f(1)}{h}= \lim_{h\rightarrow 0^-}\frac{|-1+h|+|h|-|1|}{h}
=\lim_{h\rightarrow 1^+}\frac{1-h-h-1}{h}= \lim_{h\rightarrow 0^+}\frac{-2h}{h}= -2 (|h| = - h \ because\ h < 0)
L.H.L. is not equal to R.H.L, so not differentiable at x=-1

Hence, exactly two points where it is not differentiable

Question:22 If y = \begin{vmatrix} f (x) & g(x) & h (x) \\ l& m &n \\ a& b &c \end{vmatrix} , prove that dy/dx = \begin{vmatrix} f '(x) & g'(x) & h' (x) \\ l& m &n \\ a& b &c \end{vmatrix}

Answer:

Given that
y = \begin{vmatrix} f (x) & g(x) & h (x) \\ l& m &n \\ a& b &c \end{vmatrix}
We can rewrite it as
y = f(x)(mc-bn)-g(x)(lc-an)+h(x)(lb-am)
Now, differentiate w.r.t x
we will get
\frac{dy}{dx} = f^{'}(x)(mc-bn)-g^{'}(x)(lc-an)+h^{'}(x)(lb-am) \Rightarrow \begin{bmatrix} f^{'}(x) &g^{'}(x) &h^{'}(x) \\ l&m &n \\ a& b &c \end{bmatrix}
Hence proved

Question:2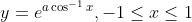3 If y = e ^{a \cos ^{-1}x} , -1 \leq x \leq 1 , show that

Answer:

Given function is

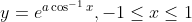
y = e ^{a \cos ^{-1}x} , -1 \leq x \leq 1

Now, differentiate w.r.t x
we will get
\frac{dy}{dx}= \frac{d(e^{a\cos^{-1}x})}{dx}.\frac{d(a\cos^{-1}x)}{dx} = e^{a\cos^{-1}x}.\frac{-a}{\sqrt{1-x^2}} -(i)
Now, again differentiate w.r.t x
\frac{d^2y}{dx^2}= \frac{d}{dx}\frac{dy}{dx}= \frac{-ae^{a\cos^{-1}x}.\frac{-a}{\sqrt{1-x^2}}.\sqrt{1-x^2}+ae^{a\cos^{-1}x}.\frac{1.(-2x)}{2\sqrt{1-x^2}}}{(\sqrt{1-x^2})^2}
=\ \frac{a^2e^{a\cos^{-1}x}-\frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}}}{1-x^2} -(ii)
Now, we need to show that
( 1- x^2 ) \frac{d^2 y }{dx ^2} - x \frac{dy}{dx} - a ^2 y = 0
Put the values from equation (i) and (ii)
(1-x^2).\left ( \ \frac{a^2e^{a\cos^{-1}x}-\frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}}}{1-x^2} \right )-x.\left ( \frac{-ae^{a\cos^{-1}x}}{\sqrt{1-x^2}} \right )-a^2e^{a\cos^{-1}x}
a^2e^{a\cos^{-1}x}-\frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}}+\left ( \frac{axe^{a\cos^{-1}x}}{\sqrt{1-x^2}} \right )-a^2e^{a\cos^{-1}x} = 0
Hence proved

More About NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise

In Class 12 Maths chapter 5 miscellaneous solutions there are 23 questions related to finding derivatives of different types of functions, second-order derivatives, and mixed concepts questions from all the previous exercises of this chapter. Before solving the exercises questions, you can try to solve solved examples given before this exercise. It will help you to get more clarity of the concept and you will be able to solve miscellaneous questions by yourself.

Also Read| Continuity and Differentiability Class 12 Chapter 5 Notes

Benefits of NCERT Solutions for Class 12 Maths Chapter 5 Miscellaneous Exercise

  • Sometimes questions from miscellaneous exercises are asked in the competitive exam so, the Class 12 Maths chapter 5 miscellaneous solutions becomes important.
  • First, try to solve NCERT problems by yourself, it will check your understanding of the concept
  • NCERT solutions for Class 12 Maths chapter 5 miscellaneous exercise can be used for reference.
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Key Features Of NCERT Solutions For Class 12 Chapter 5 Miscellaneous Exercise

  • Comprehensive Coverage: The solutions encompass all the topics covered in miscellaneous exercise class 12 chapter 5, ensuring a thorough understanding of the concepts.
  • Step-by-Step Solutions: In this class 12 chapter 5 maths miscellaneous solutions, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
  • Accuracy and Clarity: Solutions for class 12 maths miscellaneous exercise chapter 5 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
  • Conceptual Clarity: In this class 12 maths ch 5 miscellaneous exercise solutions, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
  • Inclusive Approach: Solutions for class 12 chapter 5 miscellaneous exercise cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
  • Relevance to Curriculum: The solutions for miscellaneous exercise class 12 chapter 5 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions of Class 12 Subject Wise

Subject Wise NCERT Exampler Solutions

Happy learning!!!

Frequently Asked Questions (FAQs)

1. Does questions form miscellaneous exercise are asked in the board exams?

Over 90% of questions in the board exams are not asked from the miscellaneous exercise.

2. Does multiplication of two continuous functions is a continuous function ?

Yes, the multiplication of two continuous functions is a continuous function.

3. Does subtraction of two continuous functions is a continuous function ?

Yes, subtraction of two continuous functions is a continuous function.

4. What is the weightage of chemistry in NEET ?

Chemistry holds 25% marks weighatge in the NEET exam.

5. What is the weightage of Continuity and Differentiability in CBSE Class 12 Maths board exams ?

CBSE doesn't provide chapter-wise marks distribution for CBSE Class 12 Maths. A total of 35 marks of questions are asked from the calculus in the CBSE final board exam.

6. What is the weightage of biology in NEET ?

Biology holds the 50% weightage in the NEET exam.

7. What is the weightage of maths in JEE Main?

The JEE main has an equal weightage of three subjects Physics, Chemistry, and Maths.

8. What is the maximum total marks JEE Main?

The maximum marks for JEE Main 2021 is 300 marks.

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

View All School Exams

Certifications By Top Providers

Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
November 20, 2024 - 11:17 PM IST :
CBSE Board Exams 2025: Online portal for availing exemptions by CWSN students opens
December 18, 2024 - 02:57 PM IST
Board Exams: States agree to equivalence; no question paper ‘jumbling’ from next year, says PARAKH CEO
December 12, 2024 - 12:44 PM IST
Board Exam Date 2025 Live: CBSE, ICSE, BSEB, MPBSE Class 10, 12 timetable out; Punjab, Rajasthan schedule soon
December 08, 2024 - 10:34 PM IST
CBSE Board Exams 2025: Guidelines issued for Class 10, 12 practicals
December 03, 2024 - 01:11 PM IST
Board Exam Date Sheet 2025 Live: ICSE, ISC, CBSE, MP time table out; BSEB routine soon
November 26, 2024 - 10:18 PM IST
Board exam dates 2025: CBSE, CISCE, UP, MP, Maharashtra, TN time table out; state-wise updates
November 25, 2024 - 08:42 PM IST
Board Exam Date Sheet 2025: CBSE, UPMSP, MPBSE, Class 10, 12 board exam dates out; BSEB, CGBSE schedules soon
November 22, 2024 - 10:04 PM IST

Stay up-to date with CBSE Class 12th News

Back to top