NCERT solutions for class 12 physics chapter 8 Electromagnetic Waves
Have you ever wondered how your phone can pick up radio signals or how the sun can travel millions of kilometres to hit the Earth? The solution is in electromagnetic waves, which constitute the basis of Chapter 8 of Class 12 Physics. This chapter discusses the properties, behaviour and uses of the electromagnetic waves in real life, and the NCERT Solutions of Class 12 Physics Chapter 8 - Electromagnetic Waves provide these simple and step-by-step explanations, which help students to understand them well.
The last three years’ closing ranks of all NITs for CSE courses are given below.
NIT JEE Mains cut-off | 2025 | 2024 | 2023 | |||
Institute | Opening Rank | Closing Rank | Opening Rank | Closing Rank | Opening Rank | Closing Rank |
NIT Tiruchirappalli | 659 | 1449 | 299 | 1224 | 176 | 1509 |
NIT Karnataka, Surathkal | 1191 | 1827 | 14 | 1615 | 966 | 1984 |
NIT Warangal | 1521 | 2409 | 1043 | 2186 | 889 | 2413 |
NIT Rourkela | 2442 | 3431 | 591 | 2940 | 2529 | 3786 |
Motilal Nehru National Institute of Technology Allahabad | 2730 | 4594 | 2417 | 4191 | 2758 | 4777 |
NIT Calicut | 3651 | 5222 | 2614 | 4482 | 2483 | 5256 |
Malaviya National Institute of Technology Jaipur | 3027 | 5601 | 1501 | 4711 | 2684 | 4909 |
Visvesvaraya National Institute of Technology, Nagpur | 4442 | 6359 | 4555 | 5795 | 4920 | 7087 |
NIT Kurukshetra | 5180 | 7037 | 4472 | 6000 | – | – |
NIT Delhi | 2363 | 7651 | 2438 | 8018 | 4278 | 9930 |
Sardar Vallabhbhai National Institute of Technology, Surat | 6343 | 8130 | 5587 | 7113 | 5052 | 7741 |
NIT Jamshedpur | 6378 | 8902 | 4935 | 7944 | 3260 | 9204 |
Maulana Azad National Institute of Technology Bhopal | 5942 | 9249 | 6217 | 8830 | 6409 | 9370 |
NIT Durgapur | 6565 | 9836 | 5973 | 8765 | 6848 | 10070 |
Dr. B R Ambedkar National Institute of Technology, Jalandhar | 7991 | 11262 | 6330 | 10957 | 9028 | 11017 |
NIT Hamirpur | 9637 | 12586 | 8376 | 12236 | 9929 | 12426 |
NIT Silchar | 8010 | 12665 | 5736 | 11930 | 8606 | 12818 |
NIT Raipur | 8140 | 13559 | 10323 | 13177 | 10110 | 12773 |
NIT Goa | 10279 | 13640 | 7914 | 12511 | 8584 | 12604 |
NIT Patna | 10529 | 14996 | 9288 | 14442 | 8125 | 13964 |
Indian Institute of Engineering Science and Technology, Shibpur | 13917 | 16765 | 6068 | 14635 | 8043 | 13711 |
NIT Andhra Pradesh | 11739 | 18183 | 10309 | 18548 | 11839 | 17272 |
NIT Uttarakhand | 16359 | 18491 | 14598 | 18039 | 14432 | 18447 |
NIT Puducherry | 11429 | 19758 | 6318 | 18515 | 12546 | 17305 |
NIT Agartala | 13104 | 22013 | 8121 | 20298 | 14010 | 20102 |
NIT Meghalaya | 20712 | 24074 | 14656 | 20039 | 15911 | 19175 |
NIT Srinagar | 15080 | 26171 | 12751 | 21839 | 12931 | 22814 |
NIT Sikkim | 15389 | 26616 | 23245 | 28284 | 19566 | 24093 |
NIT Arunachal Pradesh | 27500 | 30607 | 22046 | 28514 | 25273 | 29087 |
NIT Manipur | 26617 | 33098 | 15616 | 30611 | 17658 | 29644 |
NIT Mizoram | 35504 | 37751 | 31598 | 33181 | 28938 | 31336 |
NIT Nagaland | 32717 | 39594 | 22429 | 31391 | 24324 | |
JEE Main 2026: NIT Tiruchirappalli, Surathkal, Warangal retain highest BTech cut-offs among NITs
This Story also Contains
- NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves: Download PDF
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Exercise Questions
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Additional Questions
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Higher Order Thinking Skills (HOTS) Questions
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Topics
- Class 12 Physics Chapter 8 - Electromagnetic Waves: Important Formulae
- Approach to Solve Questions of Class 12 Physics Chapter 8 - Electromagnetic Waves
- How Can NCERT Solutions for Class 12 Physics Chapter 8 Help in Exam Preparation?
- What Extra Should Students Study Beyond NCERT For JEE/NEET?
- NCERT Solutions for Class 12 Physics Chapter-Wise

These NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves are very useful in the preparation of CBSE Class 12 board examination and competitive examinations such as JEE Main and NEET because they contain not only solved exercises, but also extra practice questions and an understanding of the concept. These NCERT solutions, which are designed by the subject experts, not only conserve the precious study time but also simplify the revision of the complex concepts. It is also free of cost, and the NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves PDF can be downloaded by the student, allowing one to revise anytime and anywhere conveniently. These Class 12 physics chapter 8 Electromagnetic Waves questions answers are well constructed, and thus, students are able to reinforce their fundamentals and build confidence in exams.
Also Read
NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves: Download PDF
The Class 12 Physics Chapter 8 - Electromagnetic Waves question answers help students gain a clear understanding of the concepts and reinforce their knowledge by giving out detailed and stepwise answers to all the questions present in the chapter. The Class 12 physics chapter 8 Electromagnetic Waves questions answers are crafted according to the new NCERT syllabus and are also very beneficial in preparation for the board exams and competitive exams like JEE and NEET. You may as well download the free PDF to read continuously and revise successfully.
Class 12 Physics Chapter 8 - Electromagnetic Waves: Exercise Questions
Electromagnetic Waves class 12 question answers of textbook exercises offer detailed and easy-to-understand answers to all in-text and exercise problems. These Electromagnetic Waves class 12 question answers help students grasp key concepts, practice effectively, and prepare confidently for board exams and competitive tests like JEE and NEET.
Calculate the capacitance and the rate of change of potential difference between the plates.
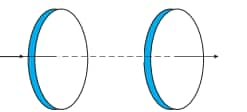
Answer:
Radius of the discs(r) = 12cm
Area of the discs(A) = $\pi r^{2}=\pi (0.12)^{2}=.045m^{2}$
Permittivity, $\epsilon _{0}$ = $8.85\times 10^{-12}C^{2}N^{-1}m^{2}$
Distance between the two discs = 5cm=0.05m
$Capacitance= \frac{\varepsilon _{0}A}{d}$
= $\frac{8.85\times 10^{-12}C^{2}N^{-1}m^{2}\times .045m^{2}}{0.05m}$
= $8.003\times 10^{-12}F$
=8.003 pF
$Rate\ of \ change\ of \ potential =\frac{dv}{dt}$
But
$V =\frac{Q}{C}$
Therefore,
$Rate\ of \ change\ of \ potential=\frac{d(\frac{Q}{C})}{dt}=\frac{dq}{Cdt}=\frac{i}{C}$
$=\frac{0.15A}{8.003pF}$
= $1.87\times 10^{10}Vs^{-1}$
1(b). Figure shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A. Obtain the displacement current across the plates.

Answer:
The value of the displacement current will be the same as that of the conduction current, which is given to be 0.15A. Therefore displacement current is also 0.15A.
1.(c) Figure 8.5 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A. Is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor? Explain.

Answer:
Yes, Kirchhoff's First rule (junction rule) is valid at each plate of the capacitor. This might not seem like the case at first, but once we take into consideration both the conduction and displacement current the Kirchhoff's first rule will hold good.
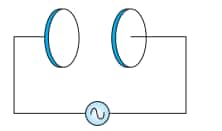
2.(a) A parallel plate capacitor made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of $300 rad s ^{-1}$. What is the rms value of the conduction current?
Answer:
Capacitance(C) of the parallel plate capacitor = 100 pF
Voltage(V) = 230 V
Angular Frequency (ω) = $300\ rad\ s^{-1}$
$Rms\ Current(I) =\frac{Voltage}{Capacitive\ Reactance}$
$Capacitive \ Reactance(X_{c})= \frac{1}{C\omega }=\frac{1}{100\ pF\times 300\ rad\ s^{-1}}$
$X_{c}= 3.33\times 10^{7} \Omega$
$I=\frac{V}{X_{c}}=\frac{230V}{3.33\times 10^{7}\Omega }= 6.9\times 10^{-6}A$
RMS value of conduction current is $6.9\mu A$
2.(b) A parallel plate capacitor (Fig. 8.6) made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of $300 rad s ^{-1}$ Is the conduction current equal to the displacement current?

Answer:
Yes, conduction current is equal to the displacement current. This will be the case because otherwise, we will get different values of the magnetic field at the same point by taking two different surfaces and applying Ampere–Maxwell Law.
2.(c) A parallel plate capacitor (Fig. 8.6) made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of $300 rad\: \: s ^{-1}$. Determine the amplitude of B at a point 3.0 cm from the axis between the plates.

Answer:
We know Ampere-Maxwell's Law,
$\oint B\cdot \vec{dl} = \mu _{0}(i_{c}+\varepsilon _{0}\frac{d\phi _{E}}{dt})$
Between the plates conduction current $i_{c}=0$.
For a loop of radius r smaller than the radius of the discs,
$\mu _{0}\varepsilon _{0}\frac{\mathrm{d} \phi _{E}}{\mathrm{d} t}=\mu _{0}i_{d}\frac{\pi r^{2}}{\pi R^{2}}=\mu _{0}i_{d}\frac{ r^{2}}{ R^{2}}$
$B(2\pi r)=\mu _{0}i_{d}\frac{r^{2}}{R^{2}}$
$B=\mu _{0}i_{d}\frac{r}{2\pi R^{2}}$
Since we have to find the amplitude of the magnetic field, we won't use the RMS value but the maximum value of the current.
$\\i_{max}=\sqrt{2}\times i_{rms}\\$
$ i_{max}=\sqrt{2}\times6.9\mu A\\$
$ i_{max}=9.76\mu A$
$\\B_{amp}=\mu _{0}i_{max}\frac{r}{2\pi R^{2}}\\$
$ B_{amp}=\frac{4\pi\times 10^{-7}\times 9.33\times 10^{-6}\times (.03) }{2\pi\times (0.06)^{2} }\\$
$ B_{amp}=1.63\times 10^{-11}T$
The amplitude of B at a point 3.0 cm from the axis between the plates is $1.63\times 10^{-11}T$.
Answer:
The speed with which these electromagnetic waves travel in a vacuum will be the same and will be equal to $3\times 10^{8}ms^{-1}$ (speed of light in vacuum).
Answer:
Since the electromagnetic wave travels along the z-direction, its electric and magnetic field vectors are lying in the x-y plane as they are mutually perpendicular.
Frequency of wave = 30 MHz
Wavelength = $\frac{Speed\ of\ light}{Frequency}$
$=\frac{3\times 10^{8}}{30\times 10^{6}}$
$=10m$ .
Answer:
Frequency range = 7.5 MHz to 12 MHz
Speed of light = $3\times 10^{8}ms^{-1}$
Wavelength corresponding to the frequency of 7.5 MHz
=$\frac{3\times 10^{8}ms^{-1}}{7.5\times 10^{6}Hz}$
$=40m$
Wavelength corresponding to the frequency of 12 MHz =
$\frac{3\times 10^{8}ms^{-1}}{12\times 10^{6}Hz}$
$=25m$
The corresponding wavelength band is 25m to 40m.
Answer:
The frequency of the electromagnetic waves produced by the oscillation of a charged particle about a mean position is equal to the frequency of the oscillation of the charged particle. Therefore, electromagnetic waves produced will have a frequency of $10^9$ Hz.
Answer:
Magnetic Field ($B_0$ )=510 nT = 510 $\times$ $10^{-9}$ T
Speed of light(c) = 3 $\times$ $10^{8}$ $ms^{-1}$
Electric Field = $B_0$ $\times$ c
= 510 $\times$ $10^{-9}$ T $\times$ 3 $\times$ $10^{8}$ $ms^{-1}$
= 153 $NC^{-1}$
Answer:
$E_0$ = 120 NC -1
$\nu =50.0\ MHz$
(a)
$Magnetic\ Field \ amplitude(B0) =\frac{E_{0}}{c}$
= $\frac{120}{3\times 10^{8}}$
$=400 nT$
Angular frequency ( $\omega$ ) = 2 $\pi \nu$
$=2$ $\times \pi \times 50$ $\times$ $10^{6}$
=3.14 $\times$ $10^{8}$ rad $s^{-1}$
Propagation constant(k)
= $\frac{2\pi }{\lambda }$
= $\frac{2\pi \nu }{\lambda\nu }$
= $\frac{\omega }{c}$
= $\frac{3.14\times 10^{8} }{3\times 10^{8}}$
=1.05 rad $m^{-1}$
Wavelength( $\lambda$ ) = $\frac{c}{\nu }$
= $\frac{3\times 10^{8}}{50\times 10^{6}}$ $= 6 m$
Assuming the electromagnetic wave propagates in the positive z-direction, the Electric field vector will be in the positive x-direction and the magnetic field vector will be in the positive y-direction, as they are mutually perpendicular and $E_{0}\times B_{0}$ gives the direction of propagation of the wave.
$\vec{E}=E_{0}sin(kx-\omega t)\hat{i}$
$= 120sin(1.05x-3.14\times 10^{8} t)NC^{-1}\hat{i}$
$\vec{B}=B_{0}sin(kx-\omega t)\hat{j}$
$= 400sin(1.05x-3.14\times 10^{8} t)\ nT\hat{j}$
Answer:
$E=h\nu=\frac{hc}{\lambda}$
$E=h\nu=\frac{6.6\times 10^{-34}\times3\times10^8}{\lambda \times1.6\times10^{-19}}eV=\frac{12.375\times 10^{-7}}{\lambda}eV$
Now substitute a different range of wavelengths in the electromagnetic spectrum to obtain the energy
| EM wave | One wavelength is taken from the range | Energy in eV |
| Radio | 1 m | $1.2375\times10^{-6}$ |
| Microwave | 1 mm | $1.2375\times10^{-3}$ |
| Infra-red | 1000 nm | 1.2375 |
| Light | 500 nm | 2.475 |
| Ultraviolet | 1nm | 1237.5 |
| X-rays | 0.01 nm | 123750 |
| Gamma rays | 0.0001 nm | 12375000 |
Answer:
Frequency( $\nu$ ) =20 $\times$ $10^{10}$ Hz
$E_0$ = 48 V$m^{-1}$
$Wavelength(\lambda) =\frac{Speed\ of\ light(c)}{Frequency (\nu )}$
= $\frac{3\times 10^{8}}{20\times 10^{10}}$
$=1.5 mm$
Answer:
The amplitude of the oscillating magnetic field(B 0 ) = $\frac{E_{0}}{c}$
$=$ $\frac{48}{3\times 10^{8}}$
$=160 nT$
Answer:
The average energy density of the Electric field(U E )
= $\frac{1}{2}\epsilon E^{2}$
= $\frac{1}{2}\epsilon (Bc)^{2}$ (as E=Bc)
= $\frac{1}{2}\epsilon \frac{B^{2}}{\mu \epsilon }$ $(c=\frac{1}{\sqrt{\mu \epsilon }})$
=$U_B$
Therefore, the average energy density of the electric field is equal to the average energy density of the Magnetic field.
Class 12 Physics Chapter 8 - Electromagnetic Waves: Additional Questions
Electromagnetic Waves NCERT Solutions of additional questions offer additional work beyond school textbook questions to learners to allow them to solidify their concept knowledge, such as the propagation of waves, energy transfer, and uses of electromagnetic waves. These are solutions which are capable of raising exam preparedness and problem-solving abilities, both on the board, as well as competitive examinations.
Answer:
$E = \left \{ ( 3.1 N/C )\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t )] \right \} \hat i$
$E = \left \{ ( 3.1 N/C )\sin [ (\frac{\pi }{2}-(( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t ))] \right \} \hat i$
The electric field vector is in the negative x-direction, and the wave propagates in the negative y-direction.
1 (b) Suppose that the electric field part of an electromagnetic wave in vacuum is $E = \left \{ ( 3.1 N/C )\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t )] \right \} \hat i$. What is the wavelength?
Answer:
From the equation of the wave given we can infer k = 1.8 rad $m^{-1}$
$Wavelength(\lambda )=\frac{2\pi }{k}$
$=\frac{2\pi }{1.8}$
$=3.49 m$
1 (c) Suppose that the electric field part of an electromagnetic wave in vacuum is $E = \left \{ ( 3.1 N/C )\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s t )] \right \} \hat i$. What is the frequency n?
Answer:
From the given equation of the electric field, we can infer angular frequency( $\omega$ ) = 5.4 $\ times$10^6 rad $s^{-1}$
$\begin{aligned} & \text { Frequency, } v=\frac{c}{\lambda}=\frac{3 \times 10^8}{3.5} \\ & \approx 85.7 \times 10^6 \mathrm{~Hz} \cong 86 \mathrm{MHz}\end{aligned}$
Answer:
From the given equation of the electric field, we can infer Electric field amplitude (E 0 ) =3.1$NC^{-1}$
$\text{Magnetic field amplitude}, (B_0) =\frac{E_{0}}{c}$
$=\frac{3.1}{3\times 10^{8}}$
=1.03 $\times$ $10^{-7}$ T
Answer:
As the electric field vector is directed along the negative x-direction and the electromagnetic wave propagates along the negative y-direction, the magnetic field vector must be directed along the negative z-direction. ( $-\hat{i}\times -\hat{k}=-\hat{j}$ )
Therefore, $\vec{B}= \left \{ B_{0}\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s )t] \right \} \hat k$
$\vec{B}= \left \{ 1.03\times 10^{-7}\cos [ ( 1.8 rad /m)y + ( 5.4 \times 10 ^6 rad /s )t] \right \}T \hat k$
Answer:
Total power which is converted into visible radiation = 5% of 100W = 5W
The above means 5J of energy is passing through the surface of a concentric sphere(with the bulb at its centre) per second.
Intensity for a sphere of radius 1m
$=\frac{5}{4\pi (1)^{2}}$
=0.398 $Wm^{-2}$
Answer:
Total power which is converted into visible radiation = 5% of 100W = 5W
The above means 5J of energy is passing through the surface of a concentric sphere(with the bulb at its centre) per second.
Intensity for a sphere of radius 10 m
$=\frac{5}{4\pi (10)^{2}}$
=3.98 $\times$ $10^{-3}$ $Wm^{-2}$
Answer:
| EM wave | One wavelength is taken from the range | Temperature $T=\frac{0.29}{\lambda}$ |
| Radio | 100 cm | $2.9\times 10^{-3}K$ |
| Microwave | 0.1cm | 2.9 K |
| Infra-red | 100000ncm | 2900K |
| Light | 50000 ncm | 5800K |
| Ultraviolet | 100ncm | $2.9\times10^{6}K$ |
| X-rays | 1 ncm | $2.9\times10^8K$ |
| Gamma rays | 0.01 nm | $2.9\times10^{10}K$ |
These numbers indicate the temperature ranges required for obtaining radiation in different parts of the spectrum
Answer:
Frequency( $\nu$ )=1057 MHz
Wavelength( $\lambda$ ) $=\frac{c}{\nu }$
$=\frac{3\times 10^{8}}{1057\times 10^{6} }$
=0.283 m
=28.3 cm
Radio waves
Answer:
Using formula, $\lambda _{m}T=0.29\ cmK$
$\lambda =\frac{0.29}{2.7}$
= 0.107cm
Microwaves.
Answer:
E=14.4 keV
Wavelength( $\lambda$ ) = $\frac{hc}{E}$
= $\frac{6.6\times 10^{-34}\times 3\times 10^{8}}{14.4\times 10^{3}\times 1.6\times 10^{-19}}$
= 0.85 $\dot{A}$
X-rays
Answer the following questions
5. (a) Long-distance radio broadcasts use short-wave bands. Why?
Answer:
Long-distance radio broadcasts use short-wave bands as these are refracted by the ionosphere.
Answer the following questions
5. (b) It is necessary to use satellites for long-distance TV transmission. Why?
Answer:
As TV signals are of high frequencies, they are not reflected by the ionosphere and therefore satellites are used to reflect them.
Answer the following questions
Answer:
X-rays are absorbed by the atmosphere, and therefore, the source of X-rays must lie outside the atmosphere to carry out X-ray astronomy. Therefore, satellites orbiting the earth are necessary, but radio waves and visible light can penetrate through the atmosphere, and therefore, optical and radio telescopes can be built on the ground.
Answer the following questions
5. (d) The small ozone layer on top of the stratosphere is crucial for human survival. Why?
Answer:
The small ozone layer on top of the stratosphere is crucial for human survival as it absorbs the ultraviolet radiation coming from the sun, which is very harmful to humans.
Answer the following questions
Answer:
If the Earth did not have an atmosphere, its average surface temperature would be lower than it is now, as in the absence of an atmosphere, there would be no greenhouse effect.
Answer the following questions
Answer:
The use of nuclear weapons would cause the formation of smoke clouds, preventing the light from the sun from reaching Earth's surface, and it would also deplete the atmosphere and therefore stop the greenhouse effect and thus doubling the cooling effect.
Class 12 Physics Chapter 8 - Electromagnetic Waves: Higher Order Thinking Skills (HOTS) Questions
Chapter 8 Higher Order Thinking Skills (HOTS) Questions provide students with an opportunity to think beyond ordinary exercises and think critically in understanding electromagnetic waves. These Electromagnetic Waves class 12 question answers also assist students to apply concepts in real life and prepare themselves well for both board exams as well as competitive ones like JEE and NEET.
Q1. A red LED emits light at 0.2 watts uniformly around it. The amplitude of the electric field of the light at a distance of 3 m from the diode is ___ V/m.
Answer:
$I=P / 4 \pi r^2$ and $p_{avg}=\frac{1}{2} \varepsilon_0 E_{o}^2$
$\therefore P / 4 \pi r^2=\left(\frac{1}{2}\right) \mathcal{E}_0 E_0^2 C$
Or $E_0=\sqrt{\frac{2 P}{4 \pi \varepsilon_0 r^2 C}}$
$\begin{aligned} & \text { Here } p=0.2 \mathrm{w}, r=3 \mathrm{~m}, c=3 \times 10^8 \mathrm{~ms}^{-2} \\ & \frac{1}{4} \pi \varepsilon_0=9 \times 10^9\end{aligned}$
$\begin{aligned} & E_0=\sqrt{\frac{2 \times 0.2 \times 9 \times 10^9}{9 \times 3 \times 10^8}} \\ & E_0=\sqrt{\frac{0.4 \times 9 \times 10^9}{27 \times 10^8}} \\ & E_0=\sqrt{\frac{36}{27}}\end{aligned}$
$E_0=1.15 \mathrm{~v} / \mathrm{m}$
Q2. The following figure shows a capacitor made of two circular plates. The capacitor is being charged by an external source which supplies a constant current equal to 0.15 A. What is the displacement current (in amperes) across plates?
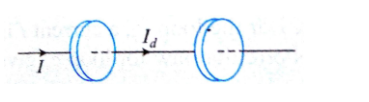
Answer:
As we know,
Displacement current
$I_d=\frac{\varepsilon_0 d \phi_c}{d t}$
But $\phi_E=E A=\frac{q}{A \varepsilon_0} A=\frac{q}{\varepsilon_0}$
$\therefore \quad I_d=\varepsilon_0 \frac{d}{d t}\left(\frac{q}{\varepsilon_0}\right)=\frac{\varepsilon_0}{\varepsilon_0} \frac{d q}{d t}=\frac{d q}{d t}=I$
Here $I=0.15 \mathrm{~A} \quad \therefore I_d=0.15 \mathrm{~A}$
Q3. A radiation of 200 W is incident on a surface which is 60% reflecting and 40% absorbing. The total force on the surface is
Answer:
Force exerted by incident radiation is $F=\frac{P}{C}$ where $P$ is the power of radiation and $C$ is the velocity of light. For absorbed radiations are $40 \%$ then exerted force is $F_{a b s}=\frac{0.4 P}{c}$ and $60 \%$ part of radiations is reflected by the surface, so force exerted by theses radiations is $$ F_{r e f}=2 \times \frac{0.6 P}{C}=\frac{1.2 P}{C} $$ Then total force exerted by radiations on the surface is $$ \begin{aligned} & F_{\text {total }}=F_{\text {ref }}+F_{\text {abs }} \\ & =\frac{1.2 P}{c}+\frac{0.4 P}{c}=\frac{1.6 P}{c} \\ & =\frac{1.6 \times 200}{3 \times 10^8}=1.07 \times 10^{-6} \mathrm{~N} \end{aligned} $$
Q4. The magnetic field of a plane electromagnetic wave is given by :
$
\vec{B}=B_0[\cos (k z-\omega t)] \hat{i}+B_1 \cos (k z+\omega t) \hat{j}
$
where $B_0=3 \times 10^{-5} T$ and $B_1=2 \times 10^{-6} \mathrm{~T}$.
The rms value of the force (in Newton) experienced by a stationary charge $Q=10^{-4} C$ at $Z=0$ is closest to (up to one decimal).
Answer:
$
\begin{aligned}
& B=B_0 \cos (k x-\omega t) \hat{i}+B_1 \cos (k z+\omega t) \hat{j} \\
& B_0=3 \times 10^{-5} T \\
& B_1=2 \times 10^{-6} T
\end{aligned}
$
Amplitude of resultant magnetic field $=B^{\prime}=\sqrt{B_o^2+B_1^2}$
$
\begin{aligned}
Q & =10^{-4} C \\
F_{r m s} & =Q E_{r m s}=Q\left(c B_{r m s}^{\prime}\right) \\
F_{r m s} & =Q \sqrt{\left(\frac{C B_0}{\sqrt{2}}\right)^2+\left(\frac{C B_1}{\sqrt{2}}\right)^2} \\
& =10^{-4} \times \frac{3 \times 10^8}{\sqrt{2}} \sqrt{\left(3 \times 10^{-5}\right)^2+\left(2 \times 10^{-6}\right)^2}
\end{aligned}
$
$
\begin{aligned}
& =10^{-4} \times \frac{3 \times 10^8}{\sqrt{2}} \sqrt{9 \times 10^{-10}+4 \times 10^{-12}} \\
& =10^{-4} \times \frac{3 \times 10^8}{\sqrt{2}} \sqrt{900 \times 10^{-12}+4 \times 10^{-12}} \\
& =\frac{3 \times 10^4}{\sqrt{2}} \sqrt{904} \times 10^{-6} \\
& =0.6 \mathrm{~N}
\end{aligned}
$
Q5. Two light waves are given by, $E_1=2 \sin (100 \pi t-k x+30)$ and $E_2=3 \cos (200 \pi t-k x+60)$. The ratio of the intensity of the first wave to that of the second wave is :
Answer:
As we learned
Intensity of EM wave -
$
I=\frac{1}{2} \epsilon_o E_o^2 c
$
where
$\epsilon_o=$ Permittivity of free space
$E_o=$ Electric field amplitude
$\mathrm{c}=$ Speed of light in vacuum
so
$
I \propto A^2 \therefore \frac{I_1}{I_2}=\frac{2^2}{3^2}=4 / 9
$
Class 12 Physics Chapter 8 - Electromagnetic Waves: Topics
Class 12 Physics Chapter 8 - Electromagnetic Waves is to explain the oscillation of electric and magnetic fields in order to transmit the energy across space. The chapter identifies the source, characteristics and uses of electromagnetic waves, which are the backbone of modern communication systems. These topics are not just some good preparation for board exams, but also a good way of learning the concepts that are helpful in JEE and NEET.
8.1 Introduction
8.2 Displacement current
8.3 Electromagnetic waves
8.3.1 Sources of electromagnetic waves
8.3.2 Nature of electromagnetic waves
8.4 Electromagnetic spectrum
8.4.1 Radio waves
8.4.2 Microwaves
8.4.3 Infrared waves
8.4.4 Visible rays
8.4.5 Ultraviolet rays
8.4.6 X-rays
8.4.7 Gamma rays
Class 12 Physics Chapter 8 - Electromagnetic Waves: Important Formulae
Class 12 Physics Chapter 8 Electromagnetic Waves explains how electric and magnetic fields combine to form waves that travel through space without needing any medium. This chapter introduces students to Maxwell’s equations, displacement current, and the nature of the electromagnetic spectrum. Learning the important formulas from this chapter helps students solve numerical problems quickly and understand the relationship between wavelength, frequency, and energy in different types of electromagnetic waves.
Displacement current:
$
I_d=\varepsilon_0 \frac{d \Phi_E}{d t}
$
Maxwell's equations (free space):
$
\begin{aligned}
& \nabla \cdot \vec{E}=\frac{\rho}{\varepsilon_0} \\
& \nabla \cdot \vec{B}=0 \\
& \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} \\
& \nabla \times \vec{B}=\mu_0 \vec{J}+\mu_0 \varepsilon_0 \frac{\partial \vec{E}}{\partial t}
\end{aligned}
$
Speed of light:
In vacuum: $c=\frac{1}{\sqrt{\mu_0 \varepsilon_0}}$
In medium: $v=\frac{c}{n}$
Angular frequency: $\omega=2 \pi f$
Wave number: $k=\frac{2 \pi}{\lambda}$
Energy densities:
Electric: $u_E=\frac{1}{2} \varepsilon_0 E^2$
Magnetic: $u_B=\frac{1}{2} \frac{B^2}{\mu_0}$
Total: $u=u_E+u_B=\varepsilon_0 E^2=\frac{B^2}{\mu_0}$
Approach to Solve Questions of Class 12 Physics Chapter 8 - Electromagnetic Waves
The electromagnetic waves are the foundation of the modern world of communication, medical science and even the transfer of energy in nature. During the process of answering questions in this chapter, the students are required to concentrate on the properties of waves and their equations and their application in real life, rather than memorisation. The systematic approach will assist in addressing the conceptual as well as the numerical issues without any problems.
- Revise Basics of Maxwell's Equations - Learn how electric and magnetic fields that vary with time produce electromagnetic waves.
- Memorise Important Formulas -Speed of EM waves, relationship between electric field (E) and magnetic field (B), energy density.
- Know the Spectrum - Learn the frequency, wavelength ranges, and other uses of various components of the electromagnetic spectrum (radio, microwave, infrared, visible, UV, X-ray, gamma).
- Concentrate on Wave Properties: Polarisation, reflection, refraction, and interaction of EM waves with objects.
- Solve Conceptual Problems -Use reasoning to solve problems in the real world, such as communication devices, satellites, and medical imaging.
- Step-by-Step approach to solving Numerical Problems - It is always important to begin with the known quantities (E, B, c, f) and use relations in a systematic manner.
- Practice Past Year questions -Work on JEE/ NEET and CBSE board questions to be acquainted with concepts that are commonly asked.
- Make Short Notes - Summarise formulas, spectrum chart, and key concepts for quick revision.
How Can NCERT Solutions for Class 12 Physics Chapter 8 Help in Exam Preparation?
Electromagnetic Waves class 12 question answers can be of great help to the students who want to perform well in their board examinations. In this chapter, the connection between magnetic and electric fields is established, and how electromagnetic waves are generated by changing fields is explained, which is a fundamental concept in the field of physics in the modern world. These Class 12 physics Electromagnetic Waves question answers can help students to have a clear idea of major concepts like the electromagnetic spectrum, characteristics of various waves, as well as their applications in various technologies such as radio, television, and satellites. Conceptual, numerical and application questions are included in these solutions as well, which intensify the problem-solving and analytical thinking. All the answers are presented in simple and exam-oriented language to assist students in writing accurate and comprehensive answers whenever undertaking exams. Moreover, revising by NCERT solutions provides total coverage of the syllabus and enables students to remember key points easily during the last-minute revision, hence one can be confident about answering questions in the board as well as in competitive exams in a more effective manner.
What Extra Should Students Study Beyond NCERT For JEE/NEET?
Beyond NCERT, students preparing for JEE/NEET should study additional concepts like Energy Density and Intensity of Electromagnetic Waves, which explain how energy is distributed in electric and magnetic fields and how it propagates through space. Understanding these topics enhances conceptual clarity and equips students to solve advanced numerical and application-based problems in competitive exams.
NCERT Solutions for Class 12 Physics Chapter-Wise
NCERT Solutions for Class 12 Physics Chapter-wise links provide a complete guide to all chapters, making it easier for students to access solved exercises, important formulas, and key concepts in one place. These solutions are designed to help students prepare effectively for board exams, JEE, NEET, and other competitive tests.
Also Check NCERT Books and NCERT Syllabus here:
- NCERT Books Class 12 Physics
- NCERT Syllabus Class 12 Physics
- NCERT Books Class 12
- NCERT Syllabus Class 12
NCERT solutions subject wise
Frequently Asked Questions (FAQs)
Light is produced by the acceleration of charged particles (photons); therefore, by the law of electromagnetism, light is an electromagnetic wave.
Electromagnetic waves have a vast range of practical everyday applications that includes such diverse uses as communication by cell phone and radio broadcasting, WiFi, cooking, vision, medical imaging, and treating cancer.
Experts at Careers360 have created the chapter 8 physics class 12 ncert solutions after completing extensive research on each concept. To assist students perform well on class assignments and board exams, every small element is well addressed. Additionally, it enables students to successfully complete their tasks on time.
Before starting the preparation of NCERT class 12 chapter 8 it is better to have an idea of chapters 1 to 7. Chapter 1 to 7 is interconnected.
One question from chapter 8 electromagnetic waves can be expected for the NEET exam. The questions can be theoretical or numerical.
From the chapter on electromagnetic waves, one question can be expected for JEE Main. More than one question can also be asked.
3 to 5 marks questions are asked from class 12 chapter electromagnetic waves for CBSE board exams.
Questions related to CBSE Class 12th
On Question asked by student community
Hello,
Yes, it's completely fine to skip this year's 12th board exams and give them next year as a reporter or private candidate, allowing you to prepare better; the process involves contacting your current school or board to register as a private candidate or for improvement exams during the specified
HELLO,
Yes i am giving you the link below through which you will be able to download the Class 12th Maths Book PDF
Here is the link :- https://school.careers360.com/ncert/ncert-book-for-class-12-maths
Hope this will help you!
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your
The CBSE Sahodaya Class 12 Pre-Board Chemistry Question Paper for the 2025-2026 session is available for download on the provided page, along with its corresponding answer key.
The Sahodaya Pre-Board exams, conducted in two rounds (Round 1 typically in December 2025 and Round 2 in January 2026), are modeled precisely
Hello,
You can get the Class 11 English Syllabus 2025-26 from the Careers360 website. This resource also provides details about exam dates, previous year papers, exam paper analysis, exam patterns, preparation tips and many more. you search in this site or you can ask question we will provide you the
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
