Aakash Repeater Courses
Take Aakash iACST and get instant scholarship on coaching programs.
Derivatives tell us how fast things change in regular life, whether it’s a falling object, rising prices, or your heart rate after a run! Now, imagine that for the school's annual day, the principal wants to decorate the school’s ballroom to its maximum capacity with fabric, ribbons, and flowers, but due to a tight budget, he needs to use the least amount of materials. Here comes the role of this chapter, Application of Derivatives, to minimise the material. The NCERT Solutions for Class 12, Application of Derivatives, cover topics such as rates of change, increasing and decreasing functions, maxima and minima, tangents and normals, and differential approximations. Experienced Careers360 subject matter experts who regularly review syllabus changes and structure learning accordingly have curated these Application of Derivatives Class 12 NCERT Solutions in a student-friendly manner.
This Story also Contains
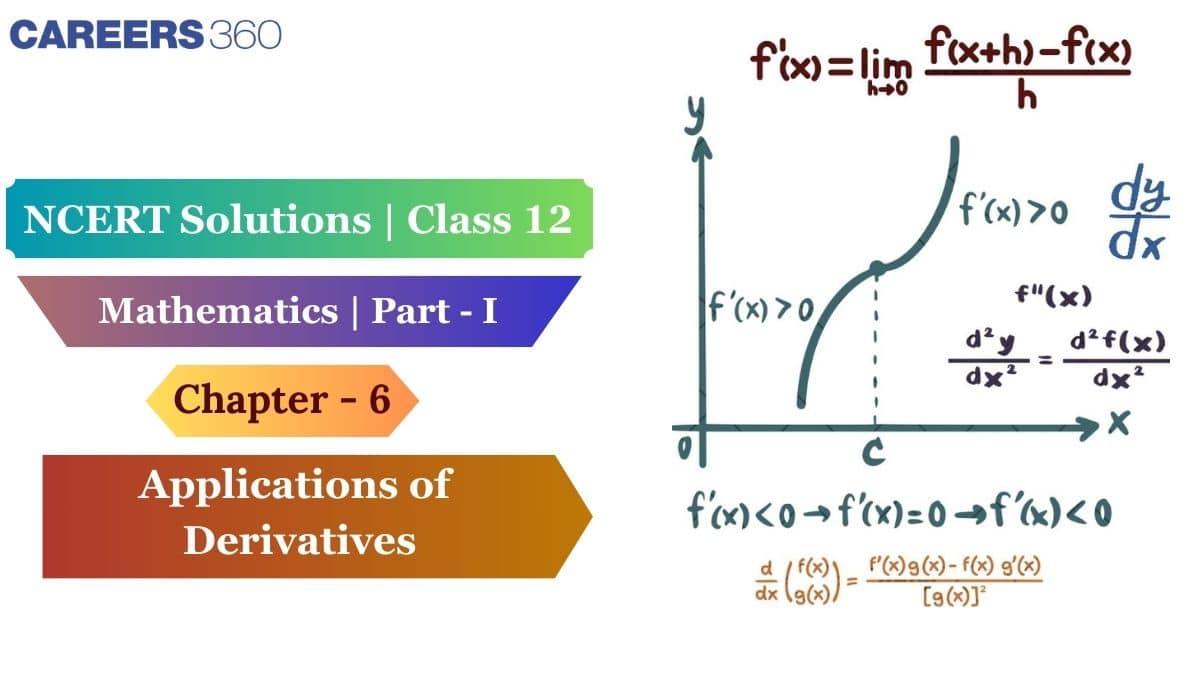
The application of derivatives chapter bridges the gap between numbers and nature, revealing how the universe changes, moment by moment. These NCERT solutions for Class 12 Maths provide step-by-step explanations and complete conceptual clarity to students. Students prefer NCERT Solutions as they make revision easier and more effective. After reviewing the Class 12 Maths Chapter 6 Solutions, students can utilise the Notes and Exemplar for a more in-depth understanding. For syllabus, notes, and PDF, refer to NCERT.
Students who wish to access the Class 12 Maths Chapter 6 Solutions PDF can click on the link given below to download the complete solution in PDF format.
|
NCERT Application of Derivatives Class 12 Solutions: Exercise 6.1 |
Question 1 (a): Find the rate of change of the area of a circle with respect to its radius r when r = 3 cm.
Answer:
Area of the circle (A) = $\pi r^{2}$, where $r=$ radius
Rate of change of the area of a circle with respect to its radius r
= $\frac{dA}{dr}$ = $\frac{d(\pi r^{2})}{dr}$ = $2 \pi r$
So, when r = 3, Rate of change of the area of a circle = $2 \pi (3)$ = $6 \pi$
Hence, the rate of change of the area of a circle with respect to its radius r when r = 3 is $6 \pi.$
Question 1 (b): Find the rate of change of the area of a circle with respect to its radius r when r = 4 cm.
Answer:
Area of the circle (A) = $\pi r^{2}$, where $r=$ radius
Rate of change of the area of a circle with respect to its radius r
= $\frac{dA}{dr}$ = $\frac{d(\pi r^{2})}{dr}$ = $2 \pi r$
So, when r = 4, Rate of change of the area of a circle = $2 \pi (4)$ = $8 \pi$
Hence, the rate of change of the area of a circle with respect to its radius r when r = 4 is $8 \pi.$
Answer:
The volume of the cube(V) = $x^{3}$ where x is the edge length of the cube
It is given that the volume of a cube is increasing at the rate of 8 cm3/s.
we can write $\frac{dV}{dt} = \frac{dV}{dx}.\frac{dx}{dt}$ ( By chain rule)
$\frac{dV}{dt} = 8 = \frac{dV}{dx}.\frac{dx}{dt}$
$\frac{dx^{3}}{dx}.\frac{dx}{dt} = 8$
$\Rightarrow 3x^{2}.\frac{dx}{dt} = 8$
$⇒\frac{dx}{dt} = \frac{8}{3x^{2}}$-----------(i)
Now, we know that the surface area of the cube(A) is $6x^{2}$.
$\frac{dA}{dt} = \frac{dA}{dx}.\frac{dx}{dt} = \frac{d(6x^{2})}{dx}.\frac{dx}{dt} = 12x. \frac{dx}{dt}$--------------(ii)
From equation (i), we know that $\frac{dx}{dt} = \frac{8}{3x^{2}}$
Putting this value in equation (i), we get,
$\frac{dA}{dt} = 12x. \frac{8}{3x^{2}} = \frac{32}{x}$
It is given in the question that the value of edge length(x) = 12 cm.
So,
$\frac{dA}{dt} = \frac{32}{12} = \frac{8}{3}$ cm3/s
Answer:
Radius of a circle is increasing uniformly at the rate $\left ( \frac{dr}{dt} \right )$ = 3 cm/s
Area of circle(A) = $\pi r^{2}$
$\frac{dA}{dt} =\frac{dA}{dr}.\frac{dr}{dt}$ (by chain rule)
$⇒\frac{dA}{dt} =\frac{d \pi r^{2}}{dr}.\frac{dr}{dt} = 2\pi r \times 3 = 6\pi r$
It is given that the value of r = 10 cm.
So,
$\frac{dA}{dt} = 6\pi \times 10 = 60\pi $ cm2/s
Hence, the rate at which the area of the circle is increasing when the radius is 10 cm is $ 60\pi$ cm2/s.
Answer:
It is given that the rate at which the edge of the cube increases $\left ( \frac{dx}{dt} \right )$ = 3 cm/s
The volume of cube = $x^{3}$
$\frac{dV}{dt} = \frac{dV}{dx}.\frac{dx}{dt}$ (By chain rule)
$⇒\frac{dV}{dt} = \frac{dx^{3}}{dx}.\frac{dx}{dt} = 3x^{2}.\frac{dx}{dt} = 3x^{2}\times 3 = 9x^{2}$ cm3/s
It is given that the value of x is 10 cm.
So,
$\frac{dV}{dt} = 9(10)^{2} = 9\times 100 = 900$ cm3/s
Hence, the rate at which the volume of the cube increases when the edge is 10 cm long is $900$ cm3/s.
Answer:
Given = $\frac{dr}{dt} = 5$ cm/s
To find = $\frac{dA}{dt}$ at r = 8 cm
Area of the circle (A) = $\pi r^{2}$
$\frac{dA}{dt} = \frac{dA}{dr}.\frac{dr}{dt}$ (by chain rule)
$⇒\frac{dA}{dt} = \frac{d\pi r^{2}}{dr}.\frac{dr}{dt} = 2\pi r \times 5 = 10\pi r = 10\pi \times 8 = 80\pi$ cm2/s
Hence, the rate at which the area increases when the radius of the circular wave is 8 cm is $80\pi$ cm2/s.
Answer:
Given = $\frac{dr}{dt} = 0.7$ cm/s
To find = $\frac{dC}{dt}$, where C is the circumference,
We know that the circumference of the circle (C) = $2\pi r$
$\frac{dC}{dt} = \frac{dC}{dr}.\frac{dr}{dt}$ (by chain rule)
$⇒\frac{dC}{dt} = \frac{d2\pi r}{dr}.\frac{dr}{dt} = 2\pi \times 0.7 = 1.4\pi$ cm/s
Hence, the rate of increase of its circumference is $1.4\pi$ cm/s.
Answer:
Given = Length x of a rectangle is decreasing at the rate $(\frac{dx}{dt})$ = -5 cm/minute (-ve sign indicates decrease in rate)
the width y is increasing at the rate $(\frac{dy}{dt})$ = 4 cm/minute
To find = $\frac{dP}{dt}$ and at x = 8 cm and y = 6 cm, where P is perimeter
Perimeter of rectangle(P) = 2(x+y)
$\frac{dP}{dt} = \frac{d(2(x+y))}{dt} = 2\left ( \frac{dx}{dt} + \frac{dy}{dt} \right ) = 2(-5+4) = -2$ cm/minute
Hence, the Perimeter decreases at the rate of 2 cm/minute.
Answer:
Given the same as the previous question.
Area of rectangle = xy
$\frac{dA}{dt} = \frac{d(xy)}{dt} = \left ( x\frac{dy}{dt} + y\frac{dx}{dt} \right ) = \left ( 8\times 4 + 6 \times (-5) \right ) = (32 -30) = 2$ cm2/minute
Hence, the rate of change of area is $2$ cm2/minute.
Answer:
Given = $\frac{dV}{dt} = 900$ cm3/s
To find = $\frac{dr}{dt}$ at r = 15 cm
Volume of sphere(V) = $\frac{4}{3}\pi r^{3}$
$\frac{dV}{dt} = \frac{dV}{dr}.\frac{dr}{dt} = \frac{d(\frac{4}{3}\pi r^{3})} {dr}.\frac{dr}{dt} = \frac{4}{3}\pi\times 3r^{2} \times \frac{dr}{dt}$
$⇒\frac{dV}{dt}= 4 \pi r^{2} \times \frac{dr}{dt}$
$⇒\frac{dr}{dt} = \frac{\frac{dV}{dt}}{4\pi r^{2}} = \frac{900}{4\pi \times(15)^{2}} = \frac{900}{900\pi} = \frac{1}{\pi}$ cm/s
Hence, the rate at which the radius of the balloon increases when the radius is 15 cm is $\frac{1}{\pi}$ cm/s.
Answer:
We need to find the value of $\frac{dV}{dr}$ at r = 10 cm
The volume of the sphere (V) = $\frac{4}{3}\pi r^{3}$
$\frac{dV}{dr} = \frac{d(\frac{4}{3}\pi r^{3})}{dr} = \frac{4}{3}\pi \times 3r^{2} = 4\pi r^{2} = 4\pi (10)^{2} = 4\pi \times 100 = 400\pi$ cm3/s
Hence, the rate at which its volume increases with the radius when the later is 10 cm is $400\pi$ cm3/s.
Answer:
Let h be the height of the ladder and x be the distance of the foot of the ladder from the wall.
It is given that $\frac{dx}{dt} = 2$ cm/s
We need to find the rate at which the height of the ladder decreases $(\frac{dh}{dt})$
length of ladder(L) = 5m and x = 4m (given)
By Pythagoras' theorem, we can say that.
$h^{2}+x^{2} = L^{2}$
$⇒h^{2} = L^{2} - x^{2}$
$⇒h= \sqrt{L^{2} - x^{2}}$
Differentiate on both sides with respect to t,
$\frac{dh}{dt}=\frac{d(\sqrt{L^{2}-x^{2}})}{dx}.\frac{dx}{dt} = \frac{1}{2}\frac{-2x}{\sqrt{5^{2}-x^{2}}}.\frac{dx}{dt} = \frac{-x}{\sqrt{25-x^{2}}}\frac{dx}{dt}$
at x = 4
$\frac{dh}{dt} = \frac{-4}{\sqrt{25-16}}\times 2 = \frac{-4}{3} \times 2 =-\frac{8}{3}$ cm/s
Hence, the rate at which the height of the ladder decreases is $\frac{8}{3}$ cm/s.
Answer:
We need to find the point at which $\frac{dy}{dt} = 8\frac{dx}{dt}$
Given the equation of curve = $6y = x^3 + 2$
Differentiate both sides w.r.t. t
$6\frac{dy}{dt} = \frac{d(x^{3})}{dx}.\frac{dx}{dt} +0$
$= 3x^{2}.\frac{dx}{dt}$
$\frac{dy}{dt} = 8\frac{dx}{dt}$ (required condition)
$⇒6\times 8\frac{dx}{dt}= 3x^{2}.\frac{dx}{dt}$
$⇒3x^{2}.\frac{dx}{dt} =48\frac{dx}{dt}$
$\Rightarrow x^{2} = \frac{48}{3} = 16$
$⇒x = \pm 4$
when x = 4, $y=\frac{4^3+2}{6}=\frac{64+2}{6}=\frac{66}{6}=11$
and
when x = -4, $y=\frac{(-4)^3+2}{6}=\frac{-64+2}{6}=\frac{-62}{6}=-\frac{31}{3}$
So, the coordinates are $(4,11)$ and $(-4,\frac{-31}{3})$.
Answer:
It is given that $\frac{dr}{dt} = \frac{1}{2}$ cm/s
We know that the shape of the air bubble is spherical.
So, volume(V) = $\frac{4}{3}\pi r^{3}$
$\frac{dV}{dt} = \frac{dV}{dr}.\frac{dr}{dt} = \frac{d(\frac{4}{3}\pi r^{3})}{dr}.\frac{dr}{dt} = 4\pi r^{2}\times\frac{1}{2} = 2\pi r^{2} = 2\pi \times (1)^{2} = 2\pi$ cm3/s
Hence, the rate of change in volume is $2\pi$ cm3/s.
Answer:
Volume of sphere(V) = $\frac{4}{3}\pi r^{3}$
Diameter = $\frac{3}{2}(2x+1)$
So, radius(r) = $\frac{3}{4}(2x+1)$
$\frac{dV}{dx} = \frac{d(\frac{4}{3}\pi r^{3})}{dx} = \frac{d(\frac{4}{3}\pi (\frac{3}{4}(2x+1))^{3})}{dx} = \frac{4}{3}\pi\times 3\times\frac{27}{64}(2x+1)^{2}\times 2$
$= \frac{27}{8}\pi (2x+1)^{2}$
Answer:
Given = $\frac{dV}{dt} = 12$ cm3/s and $h = \frac{1}{6}r$
To find = $\frac{dh}{dt}$ at h = 4 cm
Volume of cone(V) = $\frac{1}{3}\pi r^{2}h$
$\frac{dV}{dt} = \frac{dV}{dh}.\frac{dh}{dt} = \frac{d(\frac{1}{3}\pi (6h)^{2}h)}{dh}.\frac{dh}{dt} = \frac{1}{3}\pi\times36\times3h^{2}.\frac{dh}{dt} = 36\pi \times(4)^{2}.\frac{dh}{dt}$
$⇒\frac{dV}{dt} = 576\pi.\frac{dh}{dt}$
Answer:
Marginal cost (MC) = $\frac{dC}{dx}$
$C ( x) = 0.007 x^3 - 0.003 x^2 + 15 x + 4000$
$\frac{dC}{dx} = \frac{d(0.007x^{3} - 0.003x^{2}+15x+400)}{dx} = 3\times 0.007x^{2} - 2\times0.003x+15$
$= .021x^{2} - 0.006x + 15$
Now, at x = 17
MC $= 0.021(17)^{2} - 0.006(17) + 15$
$= 6.069 - 0.102 + 15$
$= 20.967$
Hence, the marginal cost when 17 units are produced is 20.967.
Answer:
Marginal revenue = $\frac{dR}{dx}$
$R (x) = 13 x^2 + 26 x + 15$
$\frac{dR}{dx} = \frac{d(13x^{2}+26x+15)}{dx} = 13\times2x+ 26 = 26(x+1)$
at x = 7
$\frac{dR}{dx} = 26(7+1) = 26\times8 = 208$
Hence, marginal revenue when x = 7 is 208.
Question 17: The rate of change of the area of a circle with respect to its radius r at r = 6 cm is (A) 10π (B) 12π (C) 8π (D) 11π
Answer:
Area of circle(A) = $\pi r^{2}$
$\frac{dA}{dr} = \frac{d(\pi r^{2})}{dr} = 2\pi r$
Now, at r = 6 cm
$\frac{dA}{dr}= 2\pi \times 6 = 12\pi$ cm2/s
Hence, the rate of change of the area of a circle with respect to its radius r at r = 6 cm is $12\pi$ cm2/s
Hence, the correct answer is B.
Answer:
Marginal revenue = $\frac{dR}{dx}$
$R ( x) = 3 x^2 + 36 x + 5$
$\frac{dR}{dx} = \frac{d(3x^{2}+36x+5)}{dx} = 3\times2x+ 36 = 6(x+6)$
at x = 15
$\frac{dR}{dx} = 6(15+6) = 6\times21 = 126$
Hence, marginal revenue when x = 15 is 126.
Hence, the correct answer is D.
|
NCERT Application of Derivatives Class 12 Solutions: Exercise 6.2 |
Question 1: Show that the function given by f (x) = 3x + 17 is increasing on R.
Answer:
Let $x_1$ and $x_2$ be two numbers in R.
$x_1 < x_2$
$ \Rightarrow 3x_1 < 3 x_2$
$ \Rightarrow 3x_1 + 17 < 3x_2+17$
$ \Rightarrow f(x_1)< f(x_2)$
Hence, f is strictly increasing on R.
Question 2: Show that the function given by $f(x) = e^{2x}$ is increasing on R.
Answer:
Let $x_1$ and $ x_2$ be two numbers in R.
$x_1 \ < \ x_2$
$ \Rightarrow 2x_1 < 2x_2$
$ \Rightarrow e^{2x_1} < e^{2x_2}$
$ \Rightarrow f(x_1) < f(x_2)$
Hence, the function $f(x) = e^{2x}$ is strictly increasing in R.
Question 3(a): Show that the function given by f (x) = $\sin x$ is increasing in $\left ( 0 , \frac{\pi}2 \right )$
Answer:
Given $f(x) = \sin x$
$f^{'}(x) = \cos x$
Since, $\cos x > 0$ for each x $\in \left ( 0,\frac{\pi}{2} \right )$
$f^{'}(x) > 0$
Hence, $f(x) = \sin x$ is strictly increasing in $\left ( 0,\frac{\pi}{2} \right )$.
Question 3(b): Show that the function given by f (x) = $\sin x$ is decreasing in $\left ( \frac{\pi}{2},\pi \right )$
Answer:
$f(x) = \sin x$
$f^{'}(x) = \cos x$
Since, $\cos x < 0$ for each $x \ \epsilon \left ( \frac{\pi}{2},\pi \right )$
So, we have $f^{'}(x) < 0$
Hence, $f(x) = \sin x$ is strictly decreasing in $\left ( \frac{\pi}{2},\pi \right )$
Question 3(c): Show that the function given by f (x) = $\sin x$ is neither increasing nor decreasing in $( 0 , \pi )$
Answer:
We know that $\sin x$ is strictly increasing in $\left ( 0,\frac{\pi}{2} \right )$ and strictly decreasing in $\left ( \frac{\pi}{2},\pi \right )$
So, by this, we can say that $f(x) = \sin x$ is neither increasing nor decreasing in the range $\left ( 0,\pi \right )$.
Question 4(a): Find the intervals in which the function f given by $f ( x) = 2x ^2 - 3 x$ is increasing
Answer:
$f ( x) = 2x ^2 - 3 x$
$f^{'}(x) = 4x - 3$
Now,
$f^{'}(x) = 0$
$⇒4x - 3 = 0$
$⇒x = \frac{3}{4}$
So, the range is $\left ( -\infty, \frac{3}{4} \right ) $ and $ \left ( \frac{3}{4}, \infty \right )$
So,
$f(x)< 0$, when $x \ \in \left ( -\infty,\frac{3}{4} \right )$ Hence, f(x) is strictly decreasing in this range
and
$f(x) > 0$, when $x \in \left ( \frac{3}{4},\infty \right )$
Hence, f(x) is strictly increasing in this range.
Hence, $f ( x) = 2x ^2 - 3 x$ is strictly increasing in $x \in \left ( \frac{3}{4},\infty \right )$
Question 4(b): Find the intervals in which the function f given by $f ( x) = 2 x ^2 - 3 x$ is decreasing
Answer:
$f ( x) = 2x ^2 - 3 x$
$f^{'}(x) = 4x - 3$
Now,
$f^{'}(x) = 0$
$⇒4x - 3 = 0$
$⇒x = \frac{3}{4}$
So, the range is $\left ( -\infty, \frac{3}{4} \right )$ and $ \left ( \frac{3}{4}, \infty \right )$.
So,
$f(x)< 0$, when $x \ \in \left ( -\infty,\frac{3}{4} \right )$ Hence, f(x) is strictly decreasing in this range
and
$f(x) > 0$, when $x \in \left ( \frac{3}{4},\infty \right )$ Hence, f(x) is strictly increasing in this range.
Hence, $f ( x) = 2x ^2 - 3 x$ is strictly decreasing in $x \in \left ( -\infty ,\frac{3}{4}\right )$.
Question 5(a): Find the intervals in which the function f given by $f (x) = 2x^3 - 3x ^2 - 36 x + 7$ is increasing
Answer:
It is given that
$f (x) = 2x^3 - 3x ^2 - 36 x + 7$
So,
$f^{'}(x)= 6x^{2} - 6x - 36$
Also, $f^{'}(x)= 0$
$⇒6x^{2} - 6x -36 =0$
$ \Rightarrow 6 (x^{2} - x-6)$
$⇒x^{2} - x-6 = 0$
$⇒x^{2} - 3x+2x-6 = 0$
$⇒x(x-3) + 2(x-3) = 0\\$
$⇒(x+2)(x-3) = 0$
$\therefore x = -2 , x = 3$
So, three ranges are there $(-\infty,-2) , (-2,3) $ and $ (3,\infty)$
Function $f^{'}(x)= 6x^{2} - 6x - 36$ is positive in interval $(-\infty,-2) , (3,\infty)$ and negative in the interval $(-2,3)$.
Hence, $f (x) = 2x^3 - 3x ^2 - 36 x + 7$ is strictly increasing in $(-\infty,-2) \cup (3,\infty)$ and strictly decreasing in the interval (-2, 3).
Question 5(b): Find the intervals in which the function f given by $f ( x) = 2x ^3 - 3x ^2 - 36x + 7$ is decreasing
Answer:
We have $f ( x) = 2x ^3 - 3x ^2 - 36x + 7$
Differentiating the function with respect to x, we get :
$f' ( x) = 6x ^2 - 6x - 36= 6\left ( x-3 \right )\left ( x+2 \right )$
When $f'(x)\ =\ 0$ , we have :
$⇒0\ = 6\left ( x-3 \right )\left ( x+2 \right )$
$⇒\left ( x-3 \right )\left ( x+2 \right )\ =\ 0$
So, three ranges are there $(-\infty,-2) , (-2,3)$ and $ (3,\infty)$
Function $f^{'}(x)= 6x^{2} - 6x - 36$ is positive in the interval $(-\infty,-2) , (3,\infty)$ and negative in the interval (-2,3)
So, f(x) is decreasing in (-2, 3).
Question 6(a): Find the intervals in which the following functions are strictly increasing or
decreasing: $x ^2 + 2x -5$
Answer:
f(x) = $x ^2 + 2x -5$
$f^{'}(x) = 2x + 2 = 2(x+1)$
Now,
$f^{'}(x) = 0 \\ 2(x+1) = 0\\ x = -1$
The range is from $(-\infty,-1) \ and \ (-1,\infty)$.
In interval $(-\infty,-1)$, $f^{'}(x)= 2(x+1)$ is -ve
Hence, function f(x) = $x ^2 + 2x -5$ is strictly decreasing in interval $(-\infty,-1)$.
In interval $(-1,\infty)$, $f^{'}(x)= 2(x+1)$ is +ve.
Hence, function f(x) = $x ^2 + 2x -5$ is strictly increasing in interval $(-1,\infty)$.
Question 6(b): Find the intervals in which the following functions are strictly increasing or
Decreasing: $10 - 6x - 2x^2$
Answer:
Given function is,
$f(x) = 10 - 6x - 2x^2$
$f^{'}(x) = -6 - 4x$
Now,
$f^{'}(x) = 0$
$⇒6+4x= 0$
$⇒x= -\frac{3}{2}$
So, the range is $(-\infty , -\frac{3}{2})$ and $ (-\frac{3}{2},\infty)$.
In interval $(-\infty , -\frac{3}{2})$ , $f^{'}(x) = -6 - 4x$ is +ve.
Hence, $f(x) = 10 - 6x - 2x^2$ is strictly increasing in the interval $(-\infty , -\frac{3}{2})$.
In interval $( -\frac{3}{2},\infty)$ , $f^{'}(x) = -6 - 4x$ is -ve.
Hence, $f(x) = 10 - 6x - 2x^2$ is strictly decreasing in interval $( -\frac{3}{2},\infty)$.
Question 6(c): Find the intervals in which the following functions are strictly increasing or
decreasing: $- 2 x^3 - 9x ^2 - 12 x + 1$
Answer:
Given function is,
$f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$
$f^{'}(x) = - 6 x^2 - 18x - 12$
Now,
$f^{'}(x) = 0\\ - 6 x^2 - 18x - 12 = 0$
$⇒-6(x^{2}+3x+2) = 0$
$⇒x^{2}+3x+2 = 0 $
$⇒x^{2} + x + 2x + 2 = 0$
$⇒x(x+1) + 2(x+1) = 0$
$⇒ (x+2)(x+1) = 0$
$\therefore x = -2$ and $x = -1$
So, the range is $(-\infty , -2) \ , (-2,-1) $ and $ (-1,\infty)$.
In interval $(-\infty , -2) \cup \ (-1,\infty)$ , $f^{'}(x) = - 6 x^2 - 18x - 12$ is -ve.
Hence, $f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$ is strictly decreasing in interval $(-\infty , -2) \cup \ (-1,\infty)$.
In interval (-2,-1) , $f^{'}(x) = - 6 x^2 - 18x - 12$ is +ve.
Hence, $f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$ is strictly increasing in the interval (-2,-1).
Question 6(d): Find the intervals in which the following functions are strictly increasing or
decreasing: $6- 9x - x ^2$
Answer:
Given function is,
$f(x) = 6- 9x - x ^2$
$f^{'}(x) = - 9 - 2x$
Now,
$f^{'}(x) = 0$
$⇒ - 9 - 2x = 0 $
$⇒2x = -9$
$⇒x = -\frac{9}{2}$
So, the range is $(-\infty, - \frac{9}{2} )$ and $ ( - \frac{9}{2}, \infty )$
In interval $(-\infty, - \frac{9}{2} )$ , $f^{'}(x) = - 9 - 2x$ is +ve.
Hence, $f(x) = 6- 9x - x ^2$ is strictly increasing in interval $(-\infty, - \frac{9}{2} )$.
In interval $( - \frac{9}{2},\infty )$ , $f^{'}(x) = - 9 - 2x$ is -ve.
Hence, $f(x) = 6- 9x - x ^2$ is strictly decreasing in interval $( - \frac{9}{2},\infty )$.
Question 6(e): Find the intervals in which the following functions are strictly increasing or
decreasing: $( x+1) ^3 ( x-3) ^3$
Answer:
Given function is,
$f(x) = ( x+1) ^3 ( x-3) ^3$
$f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$
Now,
$f^{'}(x) = 0 $
$⇒ 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^{3} =0$
$⇒3(x+1)^{2}(x-3)^{2}((x-3) + (x+1) ) = 0 $
$⇒ (x+1)(x-3) = 0$ or $(2x-2) = 0$
So, $ x=-1$ and $ x = 3$ or, $x = 1$
So, the intervals are $(-\infty,-1), (-1,1), (1,3)$ and $(3,\infty)$.
Our function $f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$ is +ve in the interval $(1,3)$ and $ (3,\infty)$.
Hence, $f(x) = ( x+1) ^3 ( x-3) ^3$ is strictly increasing in the interval $(1,3) $ and $(3,\infty)$.
Our function $f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$ is -ve in the interval $(-\infty,-1)$ and $(-1,1)$
Hence, $f(x) = ( x+1) ^3 ( x-3) ^3$ is strictly decreasing in interval $(-\infty,-1) $ and $ (-1,1)$.
Answer:
Given function is,
$f(x)\Rightarrow y = \log( 1+ x ) - \frac{2 x }{2+x }$
$f^{'}(x)\Rightarrow \frac{dy}{dx} = \frac{1}{1+x} - \frac{2 (2+x) - (1)(2x)} {(2+x)^{2} } = \frac{1}{1+x} - \frac{4+2x-2x}{(2+x)^{2}}$
$= \frac{1}{1+x} - \frac{4}{(2+x)^2}$
$= \frac{(2+x)^2 - 4(x+1)}{(x+1)(2+x)^{2}}$
$= \frac{4+x^{2} +4x -4x - 4}{(x+1)(2+x)^{2}} $
$= \frac{x^{2} }{(x+1)(2+x)^{2}}$
So, $f^{'}(x) = \frac{x^{2}}{(x+1)(x+2)^2}$
Now, for $x > -1$, it is clear that $f^{'}(x) = \frac{x^{2}}{(x+1)(x+2)^2} > 0$
Hence, $f(x)\Rightarrow y = \log( 1+ x ) - \frac{2 x }{2+x }$ strictly increasing when $x > -1$
Question 8: Find the values of x for which $y = [x(x-2)]^{2}$ is an increasing function.
Answer:
Given function is,
$f(x)\Rightarrow y = [x(x-2)]^{2}$
$f^{'}(x)\Rightarrow \frac{dy}{dx} = 2[x(x-2)][(x-2)+x]$
$= 2(x^2-2x)(2x-2)$
$= 4x(x-2)(x-1)$
Now,
$f^{'}(x) = 0$
$⇒ 4x(x-2)(x-1) = 0$
So, $ x=0 , x= 2 $ and $x = 1$
So, the intervals are $(-\infty,0),(0,1),(1,2) $ and $ (2,\infty)$
In interval $(0,1)$ and $(2,\infty)$, $f^{'}(x)> 0$
Hence, $f(x)\Rightarrow y = [x(x-2)]^{2}$ is an increasing function in the interval $(0,1)\cup (2,\infty)$.
Answer:
Given function is,
$f(x) = y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$
$f^{'}(x) = \frac{dy}{d\theta} = \frac{4 \cos \theta(2+\cos \theta) - (-\sin \theta)4\sin \theta) }{(2+ \cos \theta )^2} - 1$
$= \frac{8 \cos \theta+4\cos^2 \theta + 4\sin^2 \theta - (2+ \cos \theta )^2 }{(2+ \cos \theta )^2}$
$= \frac{8 \cos \theta+4(\cos^2 \theta + \sin^2 \theta) - 4- \cos^2 \theta - 4\cos \theta }{(2+ \cos \theta )^2}$
$= \frac{8 \cos \theta+4 - 4- \cos^2 \theta - 4\cos \theta }{(2+ \cos \theta )^2}$
$= \frac{4 \cos \theta-\cos^2 \theta }{(2+ \cos \theta )^2}$
Now, for $\theta \ \in \ [0,\frac{\pi}{2}]$
$\\ 4 \cos \theta \geq \cos^2 \theta$
$⇒4 \cos \theta - \cos^2 \geq 0$ and $(2+\cos \theta)^2 > 0$
So, $f^{'}(x) > 0$ for $\theta$ in $[0,\frac{\pi}{2}]$
Hence, $f(x) = y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$ is increasing function in $\theta \ \in [0,\frac{\pi}{2}]$.
Question 10: Prove that the logarithmic function is increasing on $( 0 , \infty )$
Answer:
Let the logarithmic function be $\log x$.
$f(x) = \log x$
$f^{'}(x) = \frac{1}{x}$
Now, for all values of x in $( 0 , \infty )$ , $f^{'}(x) > 0$
Hence, the logarithmic function $f(x) = \log x$ is increasing in the interval $( 0 , \infty )$.
Question 11: Prove that the function f given by $f ( x) = x ^2 - x + 1$ is neither strictly increasing nor decreasing on (– 1, 1).
Answer:
Given function is,
$f ( x) = x ^2 - x + 1$
$f^{'}(x) = 2x - 1$
Now, for interval $(-1,\frac{1}{2})$ , $f^{'}(x) < 0$ and for interval $(\frac{1}{2},1),f^{'}(x) > 0$
Hence, by this, we can say that $f ( x) = x ^2 - x + 1$ is neither strictly increasing nor decreasing in the interval (-1, 1).
Answer:
(A)
$f(x) = \cos x $
$ f^{'}(x) = -\sin x$
$f^{'}(x) < 0$ for x in $(0,\frac{\pi}{2})$
Hence, $f(x) = \cos x$ is decreasing function in $(0,\frac{\pi}{2})$
(B)
$f(x) = \cos 2x$
$f^{'}(x) = -2\sin2 x$
Now, as
$0 < x < \frac{\pi}{2}$
$⇒0 < 2x < \pi$
$f^{'}(x) < 0$ for 2x in $(0,\pi)$
Hence, $f(x) = \cos 2x$ is decreasing function in $(0,\frac{\pi}{2})$
(C)
$f(x) = \cos 3x $
$f^{'}(x) = -3\sin3 x$
Now, as
$0 < x < \frac{\pi}{2}$
$⇒ 0 < 3x < \frac{3\pi}{2}$
$f^{'}(x) < 0$ for $x \ \epsilon \ \left ( 0,\frac{\pi}{3} \right )$ and $f^{'}(x) > 0 \ x \ \epsilon \ \left ( \frac{\pi}{3} , \frac{\pi}{2}\right )$
Hence, it is clear that $f(x) = \cos 3x$ is neither increasing nor decreasing in $(0,\frac{\pi}{2})$
(D)
$f(x) = \tan x$
$ f^{'}(x) = \sec^{2}x$
$f^{'}(x) > 0$ for x in $(0,\frac{\pi}{2})$
Hence, $f(x) = \tan x$ is strictly increasing function in the interval $(0,\frac{\pi}{2})$.
So, only (A) and (B) are decreasing functions in $(0,\frac{\pi}{2})$.
Answer:
(A) Given function is,
$f ( x) = x ^{100} + \sin x - 1$
$f^{'}(x) = 100x^{99} + \cos x$
Now, in interval (0,1)
$f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is an increasing function in the interval (0, 1).
(B) Now, in interval $\left ( \frac{\pi}{2},\pi \right )$
$100x^{99} > 0$ but $\cos x < 0$
So, $100x^{99} > \cos x$
$⇒100x^{99} - \cos x > 0$ , $f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval $\left ( \frac{\pi}{2},\pi \right )$.
(C) Now, in interval $\left ( 0,\frac{\pi}{2} \right )$
$100x^{99} > 0 $ and $ \cos x > 0$
So, $100x^{99} > \cos x $
$⇒ 100x^{99} - \cos x > 0$, $f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval $\left ( 0,\frac{\pi}{2} \right )$.
So, $f ( x) = x ^{100} + \sin x - 1$ is increasing for all cases.
Hence, the correct answer is option (D).
Question 14: For what values of a the function f given by $f (x) = x^2 + ax + 1$ is increasing on [1, 2]?
Answer:
Given function is,
$f (x) = x^2 + ax + 1$
$f^{'}(x) = 2x + a$
Now, we can clearly see that for every value of $a > -2$
$f^{'}(x) = 2x + a$ $> 0$
Hence, $f (x) = x^2 + ax + 1$ is increasing for every value of $a > -2$ in the interval [1, 2].
Answer:
Given function is,
$f ( x) = x + \frac 1x$
$f^{'}(x) = 1 - \frac{1}{x^2}$
Now,
$f^{'}(x) = 0$
$⇒ 1 - \frac{1}{x^2} = 0$
$⇒ x^{2} = 1$
$⇒ x = \pm1$
So, intervals are from $(-\infty,-1), (-1,1)$ and $(1,\infty)$
In interval $(-\infty,-1), (1,\infty)$ , $\frac{1}{x^2} < 1 \Rightarrow 1 - \frac{1}{x^2} > 0$
$f^{'}(x) > 0$
Hence, $f ( x) = x + \frac 1x$ is increasing in interval $(-\infty,-1)\cup (1,\infty)$
In interval (-1,1), $\frac{1}{x^2} > 1 \Rightarrow 1 - \frac{1}{x^2} < 0$
$f^{'}(x) < 0$
Hence, $f ( x) = x + \frac 1x$ is decreasing in the interval (-1, 1).
Hence, the function f given by $f ( x) = x + \frac 1x$ is increasing on I disjoint from [–1, 1].
Question 16: Prove that the function f given by $f (x) = \log \sin x$ is increasing on $\left ( 0 ,\frac{\pi}2 \right )$ and decreasing on $ \left ( \frac{\pi}2 , \pi \right )$
Answer:
Given function is,
$f (x) = \log \sin x$
$f^{'}(x) = \frac{1}{\sin x}\cos x = \cot x$
Now, we know that cot x is +ve in the interval $\left ( 0 ,\frac{\pi}2 \right )$ and -ve in the interval $\left ( \frac{\pi}2 , \pi \right )$
$f^{'}(x) > 0 $ in $\left ( 0,\frac{\pi}{2} \right )$ and $ f^{'}(x) < 0$ in $ \left ( \frac{\pi}{2} , \pi \right )$
Hence, $f (x) = \log \sin x$ is increasing in the interval $\left ( 0 , \frac{\pi}2 \right )$ and decreasing in interval $\left ( \frac{\pi}2 , \pi \right )$.
Answer:
Given function is,
f(x) = log|cos x|
Value of cos x is always +ve in both these cases
So, we can write log|cos x| = log(cos x)
Now,
$f^{'}(x) = \frac{1}{\cos x}(-\sin x) = -\tan x$
We know that in interval $\left ( 0,\frac{\pi}{2} \right )$ , $\tan x > 0 \Rightarrow -\tan x< 0$
$f^{'}(x) < 0$
Hence, f(x) = log|cos x| is decreasing in interval $\left ( 0,\frac{\pi}{2} \right )$
We know that in interval $\left ( \frac{3\pi}{2},2\pi \right )$, $\tan x < 0$
$ \Rightarrow -\tan x> 0$
$f^{'}(x) > 0$
Hence, f(x) = log|cos x| is increasing in interval $\left ( \frac{3\pi}{2},2\pi \right )$.
Question 18: Prove that the function given by $f (x) = x^3 - 3x^2 + 3x - 100$ is increasing in R.
Answer:
Given function is,
$f (x) = x^3 - 3x^2 + 3x - 100$
$f^{'}(x) = 3x^2 - 6x + 3$
$⇒f^{'}(x)= 3(x^2 - 2x + 1) = 3(x-1)^2$
$⇒f^{'}(x) = 3(x-1)^2$
We can clearly see that for any value of x in R, $f^{'}(x) > 0$
Hence, $f (x) = x^3 - 3x^2 + 3x - 100$ is an increasing function in R.
Question 19: The interval in which $y = x ^2 e ^{-x}$ is increasing is
(A) $( - \infty , \infty )$ (B) $( - 2 , 0 )$ (C) $( - 2 , \infty )$ (D) $( 0, 2 )$
Answer:
Given function is,
$f(x) \Rightarrow y = x ^2 e ^{-x}$
$f^{'}(x) \Rightarrow \frac{dy}{dx} = 2x e ^{-x} + -e^{-x}(x^{2})=xe^{-x}(2-x)$
$f^{'}(x) = xe ^{-x}(2 -x)$
Now, it is clear that $f^{'}(x) > 0$ only in the interval (0, 2).
So, $f(x) \Rightarrow y = x ^2 e ^{-x}$ is an increasing function for the interval (0, 2).
Hence, the correct answer is option (D).
|
NCERT Application of Derivatives Class 12 Solutions: Exercise 6.3 |
Question 1 (i): Find the maximum and minimum values, if any, of the following functions given by ( $f (x) = (2x - 1)^2 + 3$
Answer:
Given function is,
$f (x) = (2x - 1)^2 + 3$
$(2x - 1)^2 \geq 0$
$⇒(2x-1)^2+3\geq 3$
Hence, the minimum value occurs when
$(2x-1)=0$
$⇒ x = \frac{1}{2}$
Hence, the minimum value of function $f (x) = (2x - 1)^2 + 3$ occurs at $x = \frac{1}{2}$
and the minimum value is
$f(\frac{1}{2}) = (2.\frac{1}{2}-1)^2+3\\$
$⇒f(\frac{1}{2})= (1-1)^2+3 =0+3 = 3$
and it is clear that there is no maximum value of $f (x) = (2x - 1)^2 + 3$.
Question 1(ii): Find the maximum and minimum values, if any, of the following functions given by $f (x) = 9x^ 2 + 12x + 2$
Answer:
The given function is,
$f (x) = 9x^ 2 + 12x + 2$
Adding and subtracting 2 in the given equation, we get,
$f (x) = 9x^ 2 + 12x + 2 + 2- 2$
$⇒ f(x)= 9x^2 +12x+4-2$
$⇒ f(x)= (3x+2)^2 - 2$
Now,
$(3x+2)^2 \geq 0$
$⇒ (3x+2)^2-2\geq -2$ for every $x \ \in \ R$
Hence, the minimum value occurs when
$(3x+2)=0$
$⇒x = \frac{-2}{3}$
Hence, the minimum value of function $f (x) = 9x^2+12x+2$ occurs at $x = \frac{-2}{3}$
And the minimum value is
$f(\frac{-2}{3}) = 9(\frac{-2}{3})^2+12(\frac{-2}{3})+2=4-8+2 =-2 \\$
And it is clear that there is no maximum value of $f (x) = 9x^2+12x+2$
Question 1(iii): Find the maximum and minimum values, if any, of the following functions given by $f (x) = - (x -1) ^2 + 10$
Answer:
Given function is,
$f (x) = - (x -1) ^2 + 10$
$-(x-1)^2 \leq 0$
$⇒ -(x-1)^2+10\leq 10$ for every $x \ \in \ R$
Hence, the maximum value occurs when
$(x-1)=0$
$⇒ x = 1$
Hence, maximum value of function $f (x) = - (x -1) ^2 + 10$ occurs at x = 1
and the maximum value is
$f(1) = -(1-1)^2+10=10 \\$
and it is clear that there is no minimum value of $f (x) = 9x^2+12x+2$
Question 1(iv): Find the maximum and minimum values, if any, of the following functions
given by $g(x) = x^3 + 1$
Answer:
Given function is,
$g(x) = x^3 + 1$
value of $x^3$ varies from $-\infty < x^3 < \infty$
Hence, the function $g(x) = x^3 + 1$ neither has a maximum nor a minimum value.
Question 2 (i): Find the maximum and minimum values, if any, of the following functions
given by $f (x) = |x + 2| - 1$
Answer:
The given function is
$f (x) = |x + 2| - 1$
$⇒|x+2| \geq 0$
$⇒ |x+2| - 1 \geq -1$ as $x \ \in \ R$
Hence, minimum value occurs when |x + 2| = 0
x = -2
Hence, the minimum value occurs at x = -2
And the minimum value is
$f(-2) = |-2+2| - 1 = -1$
There is no maximum value of the given function $x \ \in \ R$.
Question 2 (ii): Find the maximum and minimum values, if any, of the following functions
given by
$g(x) = - | x + 1| + 3$
Answer:
Given function is
$g(x) = - | x + 1| + 3$
$-|x+1| \leq 0$
$⇒-|x+1| + 3 \leq 3$ as $x \ \in \ R$
Hence, the maximum value occurs when -|x + 1| = 0
x = -1
Hence, the maximum value occurs at x = -1
and the maximum value is
$g(-1) = -|-1+1| + 3 = 3$
It is clear that there is no minimum value of the given function $x \ \in \ R$.
Question 2 (iii): Find the maximum and minimum values, if any, of the following functions
given by $h(x) = \sin(2x) + 5$
Answer:
The given function is
$h(x) = \sin(2x) + 5$
We know that the value of sin 2x varies from
$-1 \leq \sin2x \leq 1$
$⇒-1 + 5 \leq \sin2x +5\leq 1 +5$
$⇒ 4 \leq \sin2x +5\leq 6$
Hence, the maximum value of our function $h(x) = \sin(2x) + 5$ is 6, and the minimum value is 4.
Question 2 (iv): Find the maximum and minimum values, if any, of the following functions.
given by $f (x) = | \sin 4x + 3|$
Answer:
The given function is
$f (x) = | \sin 4x + 3|$
We know that the value of sin 4x varies from
$-1 \leq \sin4x \leq 1$
$⇒-1 + 3 \leq \sin4x +3\leq 1 +3$
$⇒ 2 \leq \sin4x +3\leq 4$
$⇒ 2\leq | \sin4x +3| \leq 4$
Hence, the maximum value of our function $f (x) = | \sin 4x + 3|$ is 4, and the minimum value is 2.
Question 2 (v): Find the maximum and minimum values, if any, of the following functions.
given by $h(x) = x + 1 , x \in ( -1,1)$
Answer:
The given function is
$h(x) = x + 1$
It is given that the value of $x \ \in (-1,1)$
So, we can not comment about either maximum or minimum value
Hence, function $h(x) = x + 1$ has neither a maximum nor a minimum value.
Answer:
Given function is
$f ( x) = x^2$
$ f^{'}(x) = 2x$
Also, $ f^{'}(x) = 0$
$ \Rightarrow 2x = 0 $
$\Rightarrow x = 0$
So, x = 0 is the only critical point of the given function.
$f^{'}(0) = 0\\$
So we find it through the 2nd derivative test.
$f^{''}(x) = 2$
$ f^{''}(0) = 2$
$f^{''}(0)> 0$
Hence, by this, we can say that 0 is a point of minima
and the minimum value is $f(0) = (0)^2 = 0$.
Answer:
Given function is
$g(x) = x ^3 - 3x$
$ g^{'}(x) = 3x^2 - 3$
$ g^{'}(x)=0$
$\Rightarrow 3x^2-3 =0$
$ \Rightarrow x = \pm 1\\$
Hence, the critical points are 1 and 1
Now, by the second derivative test
$g^{''}(x)=6x$
$g^{''}(1)=6 > 0$
Hence, 1 is the point of minima, and the minimum value is
$g(1) = (1)^3 - 3(1) = 1 - 3 = -2$
$g^{''}(-1)=-6 < 0$
Hence, -1 is the point of maxima, and the maximum value is
$g(1) = (-1)^3 - 3(-1) = -1 + 3 = 2$
Answer:
The given function is
$h(x) = \sin x + \cos x$
$ h^{'}(x)= \cos x - \sin x$
$ h^{'}(x)= 0$
$⇒ \cos x - \sin x = 0$
$⇒ \cos x = \sin x$
$⇒ x = \frac{\pi}{4}$ as $x \ \in \ \left ( 0,\frac{\pi}{2} \right )$
Now, we use the second derivative test.
$h^{''}(x)= -\sin x - \cos x$
$⇒ h^{''}(\frac{\pi}{4}) = -\sin \frac{\pi}{4} - \cos \frac{\pi}{4}$
$⇒ h^{''}(\frac{\pi}{4}) = -\frac{1}{\sqrt2}-\frac{1}{\sqrt2}$
$⇒ h^{''}(\frac{\pi}{4})= -\frac{2}{\sqrt2} = -\sqrt2 < 0$
Hence, $\frac{\pi}{4}$ is the point of maxima and the maximum value is $h\left ( \frac{\pi}{4} \right )$ which is $\sqrt2$.
Answer:
The given function is
$h(x) = \sin x - \cos x$
$ h^{'}(x)= \cos x + \sin x$
$ h^{'}(x)= 0$
$⇒ \cos x + \sin x = 0$
$⇒ \cos x = -\sin x$
$⇒ x = \frac{3\pi}{4}$ as $\ x \ \in \ \left ( 0,2\pi \right )$
Now, we use the second derivative test.
$h^{''}(x)= -\sin x + \cos x$
$⇒ h^{''}(\frac{3\pi}{4}) = -\sin \frac{3\pi}{4} + \cos \frac{3\pi}{4}$
$⇒ h^{''}(\frac{3\pi}{4}) = -(\frac{1}{\sqrt2})-\frac{1}{\sqrt2}$
$⇒ h^{''}(\frac{3\pi}{4})=- \frac{2}{\sqrt2} = -\sqrt2 < 0$
Hence, $\frac{\pi}{4}$ is the point of maxima and maximum value is $h\left ( \frac{3\pi}{4} \right )$, which is $\sqrt2$.
Answer:
Given function is:
$f (x) = x^3 - 6x^2 + 9x + 15$
$ f^{'}(x) = 3x^2 - 12x + 9$
$ f^{'}(x)= 0$
$⇒3x^2 - 12x + 9 = 0$
$⇒ 3(x^2-4x+3)=0$
$⇒x^2-4x+3 = 0$
$⇒x^2 - x -3x + 3=0$
$⇒x(x-1)-3(x-1) = 0$
$⇒(x-1)(x-3) = 0$
So, $x=1$ and $ x = 3$
Hence, 1 and 3 are critical points.
Now, we use the second derivative test.
$f^{''}(x) = 6x - 12$
$ f^{''}(1) = 6 - 12 = -6 < 0$
Hence, x = 1 is a point of maxima, and the maximum value is
$f (1) = (1)^3 - 6(1)^2 + 9(1) + 15 = 1-6+9+15 = 19$
$f^{''}(x) = 6x - 12$
$ f^{''}(3) = 18 - 12 = 6 > 0$
Hence, x = 1 is a point of minima, and the minimum value is
$f (3) = (3)^3 - 6(3)^2 + 9(3) + 15 = 27-54+27+15 = 15$
Answer:
The given function is
$g ( x) = \frac{x}{2} + \frac{2}{x}$
$ g^{'}(x) = \frac{1}{2}-\frac{2}{x^2}$
$ g^{'}(x) = 0$
$⇒ \frac{1}{2}-\frac{2}{x^2} = 0$
$⇒ x^2 = 4$
$⇒ x = \pm 2$ ( but as $x > 0$ we only take the positive value of x i.e., x = 2)
Hence, 2 is the only critical point.
Now, we use the second derivative test.
$g^{''}(x) = \frac{4}{x^3}$
$g^{''}(2) = \frac{4}{2^3} =\frac{4}{8} = \frac{1}{2}> 0$
Hence, 2 is the point of minima, and the minimum value is
$g ( x) = \frac{x}{2} + \frac{2}{x} $
$ g(2) = \frac{2}{2} + \frac{2}{2} = 1 + 1 = 2$
Answer:
The given function is
$g (x) = \frac{1}{x^2 + 2}$
$ g^{'}(x) = \frac{-2x}{(x^2+2)^2}$
$ g^{'}(x) = 0$
$ \frac{-2x}{(x^2+2)^2} = 0$
$⇒ x = 0$
Hence, x = 0 is the only critical point.
Now, we use the second derivative test.
$g^{''}(x) = -\frac{-2(x^2+2)^2-(-2x){2(x^2+2)(2x)}}{((x^2+2)^2)^2} $
$g^{''}(0) = \frac{-2\times4}{(2)^4} = \frac{-8}{16} = -\frac{1}{2}< 0$
Hence, 0 is the point of local maxima, and the maximum value is
$g (0) = \frac{1}{0^2 + 2} = \frac{1}{2}$
Answer:
The given function is
$f (x) = x \sqrt{ 1-x }$
$f ^{'}(x) = \sqrt{1-x} + \frac{x(-1)}{2\sqrt{1-x}}$
$= \sqrt{1-x} - \frac{x}{2\sqrt{1-x}} $
$\Rightarrow \frac{2-3x}{2\sqrt{1-x}}$
$ f^{'}(x) = 0$
$⇒ \frac{2-3x}{2\sqrt{1-x}} = 0$
$⇒ 3x = 2$
$⇒ x = \frac{2}{3}$
Hence, $x = \frac{2}{3}$ is the only critical point.
Now, we use the second derivative test.
$f^{''}(x)= \frac{(-1)(2\sqrt{1-x})-(2-x)(2.\frac{-1}{2\sqrt{1-x}}(-1))}{(2\sqrt{1-x})^2}$
$= \frac{-2\sqrt{1-x}-\frac{2}{\sqrt{1-x}}+\frac{x}{\sqrt{1-x}}}{4(1-x)}$
$= \frac{3x}{4(1-x)\sqrt{1-x}}$
$f^{"}(\frac{2}{3}) > 0$
Hence, it is the point of minima, and the minimum value is
$f (x) = x \sqrt{ 1-x }$
$ f(\frac{2}{3}) = \frac{2}{3}\sqrt{1-\frac{2}{3}}$
$⇒ f(\frac{2}{3}) = \frac{2}{3}\sqrt{\frac{1}{3}}$
$⇒ f(\frac{2}{3}) = \frac{2}{3\sqrt3}$
$⇒ f(\frac{2}{3}) = \frac{2\sqrt3}{9}$
Question 4(i): Prove that the following functions do not have maxima or minima: $f (x) = e^x$
Answer:
The given function is
$f (x) = e ^x$
$f^{'}(x) = e^x$
$ f^{'}(x) = 0$
$⇒ e^x=0\\$
But exponential can never be 0.
Hence, the function $f (x) = e^x$ does not have either maxima or minima.
Question 4 (ii): Prove that the following functions do not have maxima or minima: $g(x) = \log x$
Answer:
The given function is
$g(x) = \log x$
$g^{'}(x) = \frac{1}{x}$
$ g^{'}(x) = 0$
$ ⇒\frac{1}{x}= 0\\$
Since log x deifne for positive x, i.e. $x > 0$
Hence, by this, we can say that $g^{'}(x)> 0$ for any value of x.
Therefore, there is no $c \ \in \ R$ such that $g^{'}(c) = 0$
Hence, the function $g(x) = \log x$ does not have either maxima or minima.
Question 4 (iii): Prove that the following functions do not have maxima or minima: $h(x) = x^3 + x^2 + x +1$
Answer:
The given function is
$h(x) = x^3 + x^2 + x +1$
$h^{'}(x) = 3x^2+2x+1$
$ h^{'}(x) = 0$
$ ⇒3x^2+2x+1 = 0$
$ ⇒2x^2+x^2+2x+1 = 0$
$ ⇒2x^2 + (x+1)^2 = 0\\$
But, it is clear that there is no $c \ \in \ R$ such that $f^{'}(c) = 0$
Hence, the function $h(x) = x^3 + x^2 + x +1$ does not have either maxima or minima.
Answer:
The given function is
$f(x) = x^3$
$f^{'}(x) = 3x^2$
$ f^{'}(x) = 0$
$⇒ 3x^2 = 0$
$\Rightarrow x = 0$
Hence, 0 is the critical point of the function $f(x) = x^3$
Now, we need to see the value of the function $f(x) = x^3$ at x = 0 and as $x \ \epsilon \ [-2,2]$
We also need to check the value at the endpoints of the given range, i.e. x = 2 and x = -2
$f(0) = (0)^3 = 0$
$f(2= (2)^3 = 8$
$ f(-2)= (-2)^3 = -8$
Hence, maximum value of function $f(x) = x^3$ occurs at x = 2 and value is 8
and minimum value of function $f(x) = x^3$ occurs at x = -2 and value is -8.
Answer:
Given function is
$f(x) = \sin x + \cos x$
$f^{'}(x) = \cos x - \sin x$
$ f^{'}(x)= 0$
$⇒ \cos x- \sin x= 0$
$⇒ \cos = \sin x$
$⇒ x = \frac{\pi}{4}$ as $x \ \epsilon \ [0,\pi]$
Hence, $x = \frac{\pi}{4}$ is the critical point of the function $f(x) = \sin x + \cos x$
Now, we need to check the value of function $f(x) = \sin x + \cos x$ at $x = \frac{\pi}{4}$ and at the end points of given range i.e. $x = 0 \ and \ x = \pi$
$f(\frac{\pi}{4}) = \sin \frac{\pi}{4} + \cos \frac{\pi}{4}\\$
$=\frac{1}{\sqrt2}+\frac{1}{\sqrt2} = \frac{2}{\sqrt2} = \sqrt2$
$f(0) = \sin 0 + \cos 0 = 0 + 1 = 1$
$f(\pi) = \sin \pi + \cos \pi = 0 +(-1) = -1$
Hence, the absolute maximum value of function $f(x) = \sin x + \cos x$ occurs at $x = \frac{\pi}{4}$ and value is $\sqrt2$
and absolute minimum value of function $f(x) = \sin x + \cos x$ occurs at $x = \pi$ and value is -1.
Answer:
Given function is
$f(x) =4x - \frac{1}{2}x^2$
$f^{'}(x) = 4 - x $
$ f^{'}(x)= 0$
$⇒4-x= 0$
$⇒ x=4$
Hence, x = 4 is the critical point of function $f(x) =4x - \frac{1}{2}x^2$
Now, we need to check the value of function $f(x) =4x - \frac{1}{2}x^2$ at x = 4 and at the end points of given range i.e. at x = -2 and x = 9/2
$f(4) =4(4) - \frac{1}{2}(4)^2$
$=16-\frac{1}{2}.16 = 16-8 = 8$
$f(-2) = 4(-2)-\frac{1}{2}.(-2)^2 = -8-2 = -10$
$f(\frac{9}{2}) =4(\frac{9}{2})-\frac{1}{2}.\left ( \frac{9}{2} \right )^2 = 18-\frac{81}{8} = \frac{63}{8}$
Hence, absolute maximum value of function $f(x) =4x - \frac{1}{2}x^2$ occures at x = 4 and value is 8 and absolute minimum value of function $f(x) =4x - \frac{1}{2}x^2$ occures at x = -2 and value is -10.
Answer:
Given function is
$f(x) = (x-1)^2+3$
$f^{'}(x) =2(x-1)$
$f^{'}(x)= 0$
$⇒ 2(x-1)= 0$
$⇒ x=1$
Hence, x = 1 is the critical point of function $f(x) = (x-1)^2+3$
Now, we need to check the value of function $f(x) = (x-1)^2+3$ at x = 1 and at the end points of given range i.e. at x = -3 and x = 1
$f(1) = (1-1)^2+3 = 0^2+3 = 3$
$f(-3) = (-3-1)^2+3= (-4)^2+3 = 16+3= 19$
Hence, absolute maximum value of function $f(x) = (x-1)^2+3$ occurs at x = -3 and value is 19
and absolute minimum value of function $f(x) = (x-1)^2+3$ occurs at x = 1 and value is 3.
Answer:
Profit of the company is given by the function.
$p(x) = 41 - 72x - 18x ^2$
$p^{'}(x)= -72-36x$
$ p^{'}(x) = 0$
$⇒-72-36x= 0$
$⇒ x = -2$
x = -2 is the only critical point of the function $p(x) = 41 - 72x - 18x ^2$
Now, by the second derivative test, we get,
$p^{''}(x)= -36< 0$
At x = -2, $p^{''}(x)< 0$
Hence, maxima of function $p(x) = 41 - 72x - 18x ^2$ occurs at x = -2 and maximum value is
$p(-2) = 41 - 72(-2) - 18(-2) ^2=41+144-72 = 113$
Hence, the maximum profit the company can make is 113 units
Answer:
Given function is
$f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$
$f^{'}(x)=12x^3 - 24x^2 +24x - 48$
$ f^{'}(x)=0$
$⇒12(x^3-2x^2+2x-4) = 0$
$⇒ x^3-2x^2+2x-4=0\\$
Now, by hit and trial, let's first assume x = 2.
$(2)^3-2(2)^2+2(2)-4$
$= 8-8+4-4=0$
Hence, x = 2 is one value.
Now,
$\frac{x^3-2x^2+2x-4}{x-2} = \frac{(x^2+2)(x-2)}{(x-2)} = (x^2+2)$
$x^2 = - 2$ which is not possible
Hence, x = 2 is the only critical value of function $f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$
Now, we need to check the value at x = 2 and at the end points of the given range, i.e. x = 0 and x = 3
$f(2)=3(2)^4-8(2)^3+12(2)^2-48(2)+25$
$=3\times16 - 8\times 8 + 12\times 4 - 96 + 25 = 48-64+48-96+25 = -39$
$f(3)=3(3)^4 - 8(3)^3 + 12(3)^2 - 48(3) + 25$
$=3\times81-8\times27+12\times9-144+25 $
$ =243-216+108-144+25 $
$= 16$
$f(0)=3(0)^4 - 8(0)^3 + 12(0)^2 - 48(0) + 25 = 25$
Hence, maximum value of function $f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$ occurs at x = 0 and value is 25
and minimum value of function $f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$ occurs at x = 2 and value is -39.
Question 8: At what points in the interval $[ 0, 2\pi]$ does the function $\sin 2x$ attain its maximum value?
Answer:
Given function is
$f(x) = \sin 2x$
$f^{'}(x) = 2\cos 2x$
$ f^{'}(x) = 0$
$⇒ 2\cos 2x = 0$ as $ x \ \epsilon [0,2\pi]$
$0 < x < 2\pi$
$⇒ 0< 2x < 4\pi$
$⇒ \cos 2x = 0$ at $ 2x = \frac{\pi}{2},2x = \frac{3\pi}{2},2x=\frac{5\pi}{2}$ and $2x= \frac{7\pi}{2}\\$
So, the values of x are
$x = \frac{\pi}{4},x = \frac{3\pi}{4},x=\frac{5\pi}{4}$ and $x= \frac{7\pi}{4}\\$
These are the critical points of the function $f(x) = \sin 2x$
Now, we need to find the value of the function $f(x) = \sin 2x$ at $x = \frac{\pi}{4},x = \frac{3\pi}{4},x=\frac{5\pi}{4} \ and \ x= \frac{7\pi}{4}\\$ and at the end points of given range i.e. at x = 0 and $x = \pi$
$f(x) = \sin 2x$
$ f(\frac{\pi}{4}) = \sin 2\left ( \frac{\pi}{4} \right ) = \sin \frac{\pi}{2} = 1$
$f(\frac{3\pi}{4}) = \sin 2\left ( \frac{3\pi}{4} \right ) = \sin \frac{3\pi}{2} = -1$
$ f(\frac{5\pi}{4}) = \sin 2\left ( \frac{5\pi}{4} \right ) = \sin \frac{5\pi}{2} = 1$
$f(\frac{7\pi}{4}) = \sin 2\left ( \frac{7\pi}{4} \right ) = \sin \frac{7\pi}{2} = -1$
$f(\pi) = \sin 2(\pi)= \sin 2\pi = 0$
$f(0) = \sin 2(0)= \sin 0 = 0$
Hence, at $x =\frac{\pi}{4} \ and \ x = \frac{5\pi}{4}$ function $f(x) = \sin 2x$ attains its maximum value i.e. in 1 in the given range of $x \ \epsilon \ [0,2\pi]$.
Question 9: What is the maximum value of the function $\sin x + \cos x$?
Answer:
Given function is
$f(x) = \sin x + \cos x$
$f^{'}(x) = \cos x - \sin x$
$ f^{'}(x)= 0$
$⇒\cos x- \sin x= 0$
$⇒ \cos = \sin x$
$⇒x = 2n\pi+\frac{\pi}{4}$ where $n \in \ I$
Hence, $x = 2n\pi+\frac{\pi}{4}$ is the critical point of the function $f(x) = \sin x + \cos x$
Now, we need to check the value of the function $f(x) = \sin x + \cos x$ at $x = 2n\pi+\frac{\pi}{4}$
Value is the same for all cases, so let assume that n = 0
Now
$f(\frac{\pi}{4}) = \sin \frac{\pi}{4} + \cos \frac{\pi}{4}\\$
$=\frac{1}{\sqrt2}+\frac{1}{\sqrt2} = \frac{2}{\sqrt2} = \sqrt2$
Hence, the maximum value of the function $f(x) = \sin x + \cos x$ is $\sqrt2$
Answer:
Given function is
$f(x) = 2x^3-24x+107$
$f^{'}(x)=6x^2 - 24 $
$ f^{'}(x)=0$
$⇒ 6(x^2-4) = 0$
$⇒ x^2-4=0$
$⇒ x^{2} = 4$
$⇒ x = \pm2$
We neglect the value x = - 2 because $x \ \epsilon \ [1,3]$
Hence, x = 2 is the only critical value of function $f(x) = 2x^3-24x+107$
Now, we need to check the value at x = 2 and at the end points of given range, i.e. x = 1 and x = 3
$f(2) = 2(2)^3-24(2)+107\\ = 2\times 8 - 48+107\\ =16-48+107 = 75$
$f(3) = 2(3)^3-24(3)+107\\ = 2\times 27 - 72+107\\ =54-72+107 = 89$
$f(1) = 2(1)^3-24(1)+107\\ = 2\times 1 - 24+107\\ =2-24+107 = 85$
Hence, maximum value of function $f(x) = 2x^3-24x+107$ occurs at x = 3 and vale is 89 when $x \ \epsilon \ [1,3]$
Now, when $x \ \epsilon \ [-3,-1]$
We neglect the value x = 2
Hence, x = -2 is the only critical value of function $f(x) = 2x^3-24x+107$
Now, we need to check the value at x = -2 and at the end points of the given range, i.e. x = -1 and x = -3
$f(-1) = 2(-1)^3-24(-1)+107\\ = 2\times (-1) + 24+107\\ =-2+24+107 = 129$
$f(-2) = 2(-2)^3-24(-2)+107\\ = 2\times (-8) + 48+107\\ =-16+48+107 = 139$
$f(-3) = 2(-3)^3-24(-3)+107\\ = 2\times (-27) + 72+107\\ =-54+72+107 = 125$
Hence, the maximum value of function $f(x) = 2x^3-24x+107$ occurs at x = -2 and value is 139 when $x \ \epsilon \ [-3,-1]$.
Answer:
The given function is
$f(x) =x ^4 - 62x^2 + ax + 9$
Function $f(x) = x^4 - 62x^2 + ax + 9$ attains maximum value at x = 1, then x must be one of the critical points of the given function, which means
$f^{'}(1)=0$
$f^{'}(x) = 4x^3-124x+a$
$ f^{'}(1) = 4(1)^3-124(1)+a=a-120$
Now,
$f^{'}(1)=0$
$⇒ a - 120=0$
$\therefore a=120$
Hence, the value of a is 120.
Question 12: Find the maximum and minimum values of $x + \sin 2x$ on $ [ 0 , 2 \pi ]$
Answer:
The given function is
$f(x) =x+ \sin 2x$
$f^{'}(x) =1+ 2\cos 2x$
$ f^{'}(x) = 0$
$ 1+2\cos 2x = 0$ as $ x \ \epsilon \ [0,2\pi]$
$ 0 < x < 2\pi$
$⇒ 0< 2x < 4\pi$
$ \cos 2x = \frac{-1}{2}$ at $2x = 2n\pi \pm \frac{2\pi}{3}$ where $n \ \epsilon \ Z\\ x = n\pi \pm \frac{\pi}{3}$
$ x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3} \ as \ x \ \epsilon \ [0,2\pi]$
So, the values of x are:
$x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3}$
These are the critical points of the function $f(x) = x+\sin 2x$
Now, we need to find the value of the function $f(x) = x+\sin 2x$ at $x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3}$ and at the end points of given range, i.e. at x = 0 and $x = 2\pi$
$f(x) =x+ \sin 2x$
$ f(\frac{\pi}{3}) = \frac{\pi}{3}+\sin 2\left ( \frac{\pi}{3} \right ) = \frac{\pi}{3}+\sin \frac{2\pi}{3} = \frac{\pi}{3}+\frac{\sqrt3}{2}$
$ f(\frac{2\pi}{3}) = \frac{2\pi}{3}+\sin 2\left ( \frac{2\pi}{3} \right ) = \frac{2\pi}{3}+\sin \frac{4\pi}{3} = \frac{2\pi}{3}-\frac{\sqrt3}{2}$
$ f(\frac{4\pi}{3}) = \frac{4\pi}{3}+\sin 2\left ( \frac{4\pi}{3} \right ) = \frac{4\pi}{3}+\sin \frac{8\pi}{3} = \frac{4\pi}{3}+\frac{\sqrt3}{2}$
$ f(\frac{5\pi}{3}) = \frac{5\pi}{3}+\sin 2\left ( \frac{5\pi}{3} \right ) = \frac{5\pi}{3}+\sin \frac{10\pi}{3} = \frac{5\pi}{3}-\frac{\sqrt3}{2}$
$ f(2\pi) = 2\pi+\sin 2(2\pi)= 2\pi+\sin 4\pi = 2\pi$
$ f(0) = 0+\sin 2(0)= 0+\sin 0 = 0$
Hence, at $x = 2\pi$ function $f(x) = x+\sin 2x$ attains its maximum value and value is $2\pi$ in the given range of $x \ \epsilon \ [0,2\pi]$
and at x = 0 function $f(x) = x+\sin 2x$ attains its minimum value and value is 0.
Question 13: Find two numbers whose sum is 24 and whose product is as large as possible.
Answer:
Let x and y be the two numbers.
It is given that
x + y = 24
⇒ y = 24 - x
And the product of xy is maximum.
let $f(x) = xy=x(24-x)=24x-x^2$
$ f^{'}(x) = 24-2x$
$ f^{'}(x)=0$
$⇒24-2x=0$
$⇒ x=12$
Hence, x = 12 is the only critical value.
Now,
$f^{''}(x) = -2< 0$
At x= 12, $f^{''}(x) < 0$
Hence, x = 12 is the point of maxima.
Now, y = 24 - x = 24 - 12 = 12
Hence, the values of x and y are 12 and 12, respectively.
Question 14: Find two positive numbers x and y such that x + y = 60 and $xy^3$ is maximum.
Answer:
It is given that
x + y = 60
⇒ x = 60 - y
and $xy^3$ is maximum
Let $f(y) = (60-y)y^3 = 60y^3-y^4$
Now,
$f^{'}(y) = 180y^2-4y^3$
$ f^{'}(y) = 0$
So, $ y^2(180-4y)=0$
$⇒ y= 0$ and $ y = 45$
Now,
$f^{''}(y) = 360y-12y^2$
$ f^{''}(0) = 0\\$
Hence, 0 is neither a point of minima or maxima.
$f^{''}(y) = 360y-12y^2$
$ f^{''}(45) = 360(45)-12(45)^2 = -8100 < 0$
Hence, y = 45 is a point of maxima.
x = 60 - y = 60 - 45 = 15
Hence, the values of x and y are 15 and 45, respectively.
Question 15: Find two positive numbers x and y such that their sum is 35 and the product $ x^2y^5$ is a maximum.
Answer:
It is given that
x + y = 35
⇒ x = 35 - y
and $x^2 y^5$ is maximum
Therefore,
Let $ f (y )= (35-y)^2y^5\\ = (1225-70y+y^2)y^5$
$ f(y)=1225y^5-70y^6+y^7$
Now,
$f^{'}(y) = 6125y^4-420y^5+7y^6$
$ f^{'}(y)=0$
So, $ y^4(6125-420y+7y^2) = 0 $
$⇒y =0 $ and $ (y-25)(y-35)$
$\Rightarrow y = 25 , y=35$
Now,
$f^{''}(y)= 24500y^3-2100y^4+42y^5$
$f^{''}(35)= 24500(35)^3-2100(35)^4+42(35)^5 = 105043750 > 0$
Hence, y = 35 is the point of minima.
$f^{''}(0)= 0\\$
Hence, y = 0 is neither a point of maxima or minima.
$f^{''}(25)= 24500(25)^3-2100(25)^4+42(25)^5 = -27343750 < 0$
Hence, y = 25 is the point of maxima
x = 35 - y = 35 - 25 = 10
Hence, the values of x and y are 10 and 25, respectively.
Question 16: Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Answer:
Let x and y be two positive numbers.
It is given that
x + y = 16
⇒ y = 16 - x
and $x^3 + y^3$ is minimum.
$f(x) = x^3 + (16-x)^3$
Now,
$f^{'}(x) = 3x^2 + 3(16-x)^2(-1)$
$f^{'}(x) = 0$
$⇒ 3x^2 - 3(16-x)^2 =0$
$ ⇒3x^2-3(256+x^2-32x) = 0$
$⇒ 3x^2 -3x^2+96x-768= 0$
$⇒ 96x = 768$
$⇒ x = 8$
Hence, x = 8 is the only critical point.
Now,
$f^{''}(x) = 6x - 6(16-x)(-1) = 6x + 96 - 6x = 96$
$⇒ f^{''}(x) = 96$
$f^{''}(8) = 96 > 0$
Hence, x = 8 is the point of minima
y = 16 - x = 16 - 8 = 8
Hence, the values of x and y are 8 and 8, respectively.
Answer:
It is given that the side of the square is 18 cm.
Let's assume that the length of the side of the square to be cut off is x cm.
So, by this, we can say that the breadth of the cube is (18 - 2x) cm and the height is x cm.
Then,
Volume of cube $\left ( V(x) \right )$ = $x(18-2x)^2$
$V^{'}(x) = (18-2x)^2+(x)2(18-2x)(-2)$
$V^{'}(x) = 0$
$ (18-2x)^2-4x(18-2x)=0$
$⇒ 324 + 4x^2 - 72x - 72x + 8x^2 = 0$
$⇒12x^2-144x+324 = 0$
$⇒12(x^2-12x+27) = 0$
$⇒ x^2-9x-3x+27=0$
$⇒ (x-3)(x-9)=0$
$x = 3$ and $x = 9$.
But the value of x cannot be 9 because then the value of breath becomes 0.
So, we neglect value x = 9
Hence, x = 3 is the critical point.
Now,
$V^{''}(x) = 24x -144$
$ V^{''}(3) = 24\times 3 - 144 = 72 - 144 = -72$
$ V^{''}(3) < 0$
Hence, x = 3 is the point of maxima
Hence, the length of the side of the square to be cut off is 3 cm, so that the volume of the box is the maximum possible.
Answer:
It is given that the sides of the rectangle are 45 cm and 24 cm.
Let us assume the side of the square to be cut off is x cm.
Then,
Volume of cube $V(x) = x(45-2x)(24-2x)$
$V^{'}(x) = (45-2x)(24-2x) + (-2)(x)(24-2x)+(-2)(x)(45-2x)\\$
$=1080 + 4x^2 - 138x - 48x + 4x^2 - 90x +4x^2$
$= 12x^2 - 276x + 1080$
$V^{'}(x) = 0$
$ ⇒12(x^2 - 23x+90)=0$
$ ⇒x^2-23x+90 = 0$
$ ⇒x^2-18x-5x+23=0$
$⇒ (x-18)(x-5)=0$
So, $ x =18$ and $ x = 5$
But x cannot be equal to 18 because then the side (24 - 2x) becomes negative, which is not possible, so we neglect the value x = 18
Hence, x = 5 is the critical value.
Now,
$V^{''}(x)=24x-276$
$ ⇒V^{''}(5)=24\times5 - 276$
$⇒ V^{''}(5)= -156 < 0$
Hence, x = 5 is the point of maxima.
Hence, the side of the square to be cut off is 5 cm so that the volume of the box is maximum.
Question 19: Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Answer:
Let us assume that the length and breadth of the rectangle inscribed in a circle are l and b, respectively, and the radius of the circle is r.
Now, by Pythagoras' theorem,
$a = \sqrt{l^2+b^2}\\$
a = 2r [Given]
$⇒4r^2 = l^2+b^2$
$⇒ l = \sqrt{4r^2 - b^2}$
Now, area of reactangle(A) = l $\times$ b
$A(b) = b(\sqrt{4r^2-b^2})$
$A^{'}(b) = \sqrt{4r^2-b^2}+b.\frac{(-2b)}{2\sqrt{4r^2-b^2}}\\ = \frac{4r^2-b^2-b^2}{\sqrt{4r^2-b^2}} = \frac{4r^2-2b^2}{\sqrt{4r^2-b^2}}$
$A^{'}(b) = 0 $
$⇒ \frac{4r^2-2b^2}{\sqrt{4r^2-b^2}} = 0$
$⇒ 4r^2 = 2b^2$
$⇒b = \sqrt2r$
Now,
$A^{''}(b) = \frac{-4b(\sqrt{4r^2-b^2})-(4r^2-2b^2).\left ( \frac{-1}{2(4r^2-b^2)^\frac{3}{2}}.(-2b) \right )}{(\sqrt{4r^2-b^2})^2}$
$⇒ A^{''}(\sqrt2r) = \frac{(-4b)\times\sqrt2r}{(\sqrt2r)^2} = \frac{-2\sqrt2b}{r}< 0$
Hence, $b = \sqrt2r$ is the point of maxima.
$l = \sqrt{4r^2-b^2}=\sqrt{4r^2-2r^2}= \sqrt2r$
Since l = b, we can say that the given rectangle is a square.
Hence, of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Answer:
Let r be the radius of the base of the cylinder and h be the height of the cylinder.
we know that the surface area of the cylinder $(A) = 2\pi r(r+h)$
$h = \frac{A-2\pi r^2}{2\pi r}$
Volume of a cylinder
$(V) = \pi r^2 h\\ = \pi r^2 \left ( \frac{A-2\pi r^2}{2\pi r} \right ) = r \left ( \frac{A-2\pi r^2}{2 } \right )$
$V^{'}(r)= \left ( \frac{A-2\pi r^2}{2} \right )+(r).(-2\pi r)\\ = \frac{A-2\pi r^2 -4\pi r^2}{2} = \frac{A-6\pi r^2}{2}$
$V^{'}(r)= 0 $
$⇒ \frac{A-6\pi r^2}{2} = 0$
$⇒ r = \sqrt{\frac{A}{6\pi}}$
Hence, $r = \sqrt{\frac{A}{6\pi}}$ is the critical point.
Now,
$V^{''}(r) = -6\pi r$
$⇒ V^{''}(\sqrt{\frac{A}{6\pi}}) = - 6\pi . \sqrt{\frac{A}{6\pi}} = - \sqrt{6\pi A} < 0$
Hence, $r = \sqrt{\frac{A}{6\pi}}$ is the point of maxima.
$h = \frac{A-2\pi r^2}{2\pi r} = \frac{2-2\pi \frac{A}{6\pi}}{2\pi \sqrt \frac{A} {6\pi}} = \frac{4\pi \frac{A}{6\pi}}{2\pi \sqrt \frac{A} {6\pi}} = 2\pi \sqrt \frac{A} {6\pi} = 2r$
Hence, the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter(D = 2r) of the base.
Answer:
Let r be the radius of the base and h be the height of the cylinder.
The volume of the cube (V) = $\pi r^2 h$
It is given that the volume of the cylinder = 100 $cm^3$
$\pi r^2 h = 100$
$\Rightarrow h = \frac{100}{\pi r^2}$
Surface area of cube(A) = $2\pi r(r+h)$
$A(r)= 2\pi r(r+\frac{100}{\pi r^2})$
$= 2\pi r ( \frac{\pi r^3+100}{\pi r^2}) = \frac{2\pi r^3+200}{ r} = 2\pi r^2+\frac{200}{r}$
$A^{'}(r) = 4\pi r + \frac{(-200)}{r^2} $
$A^{'}(r)= 0$
$⇒ 4\pi r^3 = 200$
$⇒ r^3 = \frac{50}{\pi}$
$⇒ r = \left ( \frac{50}{\pi} \right )^{\frac{1}{3}}$
Hence, $r = (\frac{50}{\pi})^\frac{1}{3}$ is the critical point.
$A^{''}(r) = 4\pi + \frac{400r}{r^3}\\ A^{''}\left ( (\frac{50}{\pi})^\frac{1}{3} \right )= 4\pi + \frac{400}{\left ( (\frac{50}{\pi})^\frac{1}{3} \right )^2} > 0$
Hence, $r = (\frac{50}{\pi})^\frac{1}{3}$ is the point of minima.
$h = \frac{100}{\pi r^2} = \frac{100}{\pi \left ( (\frac{50}{\pi})^\frac{1}{3} \right )^2} = 2.(\frac{50}{\pi})^\frac{1}{3}$
Hence, $r = (\frac{50}{\pi})^\frac{1}{3}$ and $h = 2.(\frac{50}{\pi})^\frac{1}{3}$ are the dimensions of the can which has the minimum surface area.
Answer:
Area of the square (A) = $a^2$, $a$ = side length
Area of the circle(S) = $\pi r^2$, $r$ = radius
Given the length of the wire = 28 m
Let the length of one of the pieces be x m.
Then the length of the other piece is (28 - x) m
Now,
$4a = x$
$\Rightarrow a = \frac{x}{4}$
and
$2 \pi r = (28-x)$
$ \Rightarrow r= \frac{28-x}{2\pi}$
Area of the combined circle and square $f(x)$ = A + S
$=a^2 + \pi r^2 = (\frac{x}{4})^2+\pi (\frac{28-x}{2\pi})^2$
$f^{'}(x) = \frac{2x}{16}+\frac{(28-x)(-1)}{2\pi} $
$⇒ f^{'}(x) = \frac{x\pi+4x-112}{8\pi}$
$ f^{'}(x) = 0$
$⇒ \frac{x\pi+4x-112}{8\pi} = 0$
$⇒x(\pi+4) = 112$
$⇒x = \frac{112}{\pi + 4}$
Now,
$f^{''}(x) = \frac{1}{8}+ \frac{1}{2\pi}$
$ f^{''}(\frac{112}{\pi+4}) = \frac{1}{8}+ \frac{1}{2\pi} > 0$
Hence, $x = \frac{112}{\pi+4}$ is the point of minima.
Other length = 28 - x
= $28 - \frac{112}{\pi+4} = \frac{28\pi+112-112}{\pi+4} = \frac{28\pi}{\pi+4}$
Hence, two lengths are $\frac{28\pi}{\pi+4}$ and $\frac{112}{\pi+4}$.
Answer:
Volume of cone (V) = $\frac{1}{3}\pi R^2h$
Volume of sphere with radius r = $\frac{4}{3}\pi r^3$
By Pythagoras theorem in $\Delta ADC$, we can say that,
$OD^2 = r^2 - R^2 $
$⇒OD = \sqrt{r^2 - R^2}$
$⇒ h = AD = r + OD = r + \sqrt{r^2 - R^2}$
V = $\frac{1}{3}\pi R^2 (r + \sqrt{r^2+R^2})\\ = \frac{1}{3}\pi R^2r + \frac{1}{3}\pi R^2 \sqrt{r^2+R^2}$
$ V^{'}(R)= \frac{2}{3}\pi Rr + \frac{2}{3}\pi R \sqrt{r^2-R^2}+\frac{1}{3}\pi R^2.\frac{-2R}{2\sqrt{r^2-R^2}}$
$ V^{'}(R) = 0$
$⇒ \frac{1}{3}\pi R \left ( 2r + 2\sqrt{r^2-R^2} - \frac{R^2}{\sqrt{r^2-R^2}} \right ) = 0$
$⇒ \frac{1}{3}\pi R \left ( \frac{2r\sqrt{r^2-R^2} + 2r^2-2R^2 -R^2}{\sqrt{r^2-R^2}} \right ) = 0$
$⇒R \neq 0$ So, $2r\sqrt{r^2-R^2} = 3R^2 - 2r^2$
Square both sides, we get,
$4r^4-4r^2R^2 = 9R^4 + 4r^4 - 12R^2r^2$
$⇒9R^4-8R^2r^2 = 0$
$⇒R^2(9R^2-8r^2) = 0$
$⇒ R \neq 0$
So, $9R^2 = 8r^2$
$⇒R = \frac{2\sqrt2r}{3}$
Now,
$V^{''}(R)= \frac{2}{3}\pi r + \frac{2}{3}\pi \sqrt{r^2-R^2}+\frac{2}{3}\pi R.\frac{-2R}{2\sqrt{r^2-R^2}}-\frac{3\pi R^2}{\sqrt{r^2-R^2}} - \frac{(-1)(-2R)}{(r^2+R^2)\frac{3}{2}}$
$ V^{''}(\frac{2\sqrt2r}{3}) < 0$
Hence, point $R = \frac{2\sqrt2r}{3}$ is the point of maxima.
$h = r + \sqrt{r^2-R^2} = r + \sqrt{r^2-\frac{8r^2}{9}} = r + \frac{r}{3} = \frac{4r}{3}$
Hence, the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is $\frac{4r}{3}$.
Volume = $= \frac{1}{3}\pi R^2h = \frac{1}{3}\pi \frac{8r^2}{9}.\frac{4r}{3} = \frac{8}{27}.\frac{4}{3}\pi r^3 = \frac{8}{27}\times$ Volume of the sphere
Hence, it is proved.
Answer:
Volume of cone(V) $=\frac{1}{3}\pi r^2h$
$ \Rightarrow h = \frac{3V}{\pi r^2}$
curved surface area(A) = $\pi r l$
$l^2 = r^2 + h^2\\ l = \sqrt{r^2+\frac{9V^2}{\pi^2r^4}}$
$A = \pi r \sqrt{r^2+\frac{9V^2}{\pi^2r^4}} = \pi r^2 \sqrt{1+\frac{9V^2}{\pi^2r^6}}$
$\frac{dA}{dr} = 2\pi r \sqrt{1+\frac{9V^2}{\pi^2r^6}}+ \pi r^2.\frac{1}{2\sqrt{1+\frac{9V^2}{\pi^2r^6}}}.\frac{(-6r^5)9V^2}{\pi^2r^7}$
$ \frac{dA}{dr} = 0$
$ ⇒2\pi r \sqrt{1+\frac{9V^2}{\pi^2r^6}}+ \pi r^2.\frac{1}{2\sqrt{1+\frac{9V^2}{\pi^2r^6}}}.\frac{(-6)9V^2}{\pi^2r^7} = 0 $
$⇒ 2\pi^2r^6\left ( 1+\frac{9V^2}{\pi^2r^6} \right ) = {27V^2}$
$⇒ 2\pi^2r^6\left ( \frac{\pi^2r^6+9V^2}{\pi^2r^6} \right ) = {27V^2}$
$⇒ 2\pi^2r^6 + 18V^2 = 27V^2$
$ ⇒2\pi^2r^6 = 9V^2$
$ ⇒r^6 = \frac{9V^2}{2\pi^2}$
Now, we can verify that,
$\frac{d^2A}{dr^2} > 0$
when $r^6 =\frac{9V^2}{2\pi^2}$
Hence, $r^6 =\frac{9V^2}{2\pi^2}$ is the point of minima.
$V = \frac{\sqrt2\pi r^3}{3}$
$h = \frac{3V}{\pi r^2} = \frac{3.\frac{\sqrt2\pi r^3}{3}}{\pi r^2} = \sqrt2 r$
Hence, proved that the right circular cone of least curved surface and given volume has an altitude equal to $\sqrt 2$ times the radius of the base.
Question 25: Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is $\tan ^{-1} \sqrt 2$
Answer:
Let a be the semi-vertical angle of the cone.
Let r, h, and l be the radius, height, and slant height of the cone.
Now,
$r = l\sin a$ and $h=l\cos a$
We know that
Volume of cone (V) = $\frac{1}{3}\pi r^2 h = \frac{1}{3}\pi (l\sin a)^2(l\cos a) = \frac{\pi l^3\sin^2 a\cos a}{3}$
Now,
$\frac{dV}{da}= \frac{\pi l^3}{3}\left ( 2\sin a\cos a.\cos a+\sin^2a.(-\sin a)\right )= \frac{\pi l^3}{3}\left ( 2\sin a\cos^2a-\sin^3a \right )$
$\frac{dV}{da}=0$
$⇒ \frac{\pi l^3}{3}\left ( 2\sin a\cos^2a-\sin^3a \right ) = 0$
$⇒ 2\sin a\cos^2a-\sin^3a= 0$
$⇒ 2\sin a\cos^2a=\sin^3a$
$⇒ \tan^2 a = 2$
$⇒ a = \tan^{-1}\sqrt 2$
Now,
$\frac{d^2V}{da^2}= \frac{\pi l^3}{3}\left ( 2\cos a\cos^2a+2\cos a(-2\cos a\sin a+3\sin^2a\cos a) \right )$
Now, at $a= \tan ^{-1}\sqrt 2$
$\frac{d^2V}{dx^2}< 0$
Therefore, $a= \tan ^{-1}\sqrt 2$ is the point of maxima
Hence, it is proved.
Answer:
Let r, l, and h be the radius, slant height and height of the cone, respectively.
Now,
$r = l\sin a $ and $ h =l\cos a$
Now,
We know that
The surface area of the cone (A) = $\pi r (r+l)$
$A= \pi l\sin a l(\sin a+1)$
$⇒l^2 = \frac{A}{\pi \sin a(\sin a+1)}$
$⇒ l = \sqrt{\frac{A}{\pi \sin a(\sin a+1)}}$
Now,
Volume of cone(V) =
$\frac{1}{3}\pi r^2h = \frac{1}{3}\pi l^3 \sin^2 a\cos a= \frac{\pi}{3}.\left ( \frac{A}{\pi\sin a(\sin a+1)} \right )^\frac{3}{2}.\sin^2 a\cos a$
On differentiate it w.r.t to a and after that
$\frac{dV}{da}= 0$
We will get
$a = \sin^{-1}\frac{1}{3}$
Now, at $a = \sin^{-1}\frac{1}{3}$
$\frac{d^2V}{da^2}<0$
Hence, we can say that $a = \sin^{-1}\frac{1}{3}$ is the point if maxima
Hence, it is proved.
Question 27: The point on the curve $x^2 = 2y$ which is nearest to the point (0, 5) is
$(A) (2 \sqrt 2,4) \: \: (B) (2 \sqrt 2,0)\: \: (C) (0, 0)\: \: (D) (2, 2)$
Answer:
Given curve is $x^2 = 2y$
Let the points on curve be $\left ( x, \frac{x^2}{2} \right )$
The distance between two points is given by
$f(x)= \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
$= \sqrt{(x-0)^2+(\frac{x^2}{2}-5)^2} = \sqrt{x^2+ \frac{x^4}{4}-5x^2+25} = \sqrt{ \frac{x^4}{4}-4x^2+25}$
$f^{'}(x) = \frac{x^3-8x}{2\sqrt{\frac{x^4}{4}-4x^2+25}}$
$ f^{'}(x)= 0$
$⇒ \frac{x^3-8x}{2\sqrt{\frac{x^4}{4}-4x^2+25}} =0$
$⇒x(x^2 - 8)=0$
$⇒x=0 $ and
$x^2 = 8$
$\Rightarrow x = 2\sqrt2$
$\begin{aligned} & f^{\prime \prime}(x)=\frac{1}{2}\left(\frac{\left(3 x^2-8\right)\left(\sqrt{\frac{x^4}{4}-4 x^2+25}-\left(x^3-8 x\right) \cdot \frac{\left(x^3-8 x\right)}{\left(2 \sqrt{\frac{x^4}{4}-4 x^2+25}\right.}\right)}{\left(\sqrt{\frac{x^4}{4}-4 x^2+25}\right)^2}\right)\end{aligned}$
$f^{''}(0) = -8 < 0$
Hence, x = 0 is the point of maxima.
$f^{''}(2\sqrt2) > 0$
Hence, the point $x = 2\sqrt2$ is the point of minima
$x^2 = 2y$
$\Rightarrow y = \frac{x^2}{2} = \frac{8}{2}=4$
Hence, the point $(2\sqrt2,4)$ is the point on the curve $x^2 = 2y$ which is nearest to the point (0, 5)
Hence, the correct answer is option (A).
Question 28: For all real values of x, the minimum value of $\frac{1- x + x^2 }{1+ x +x^2}$
is: (A) 0 (B) 1 (C) 3 (D) $\frac13$
Answer:
The given function is
$f(x)= \frac{1- x + x^2 }{1+ x +x^2}$
$f^{'}(x)= \frac{(-1+2x)(1+x+x^2)-(1-x+x^2)(1+2x)}{(1+ x +x^2)^2}$
$⇒f^{'}(x)= \frac{-1-x-x^2+2x+2x^2+2x^3-1-2x+x+2x^2-x^2-2x^3}{(1+ x +x^2)^2} = \frac{-2+2x^2}{(1+ x +x^2)^2}$
$f^{'}(x)=0$
$⇒ \frac{-2+2x^2}{(1+ x +x^2)^2} = 0$
$ ⇒x^2 = 1$
$⇒ x= \pm 1$
Hence, x = 1 and x = -1 are the critical points.
Now,
$f^{''}(x)= \frac{4x(1+ x +x^2)^2-(-2+2x^2)2(1+x+x^2)(2x+1)}{(1+ x +x^2)^4}$
$f^{''}(1) = \frac{4\times(3)^2}{3^4} = \frac{4}{9} > 0$
Hence, x = 1 is the point of minima, and the minimum value is
$f(1)= \frac{1- 1 + 1^2 }{1+ 1 +1^2} = \frac{1}{3}$
$f^{''}(-1) =-4 < 0$
Hence, x = -1 is the point of maxima.
Hence, the minimum value of
$\frac{1- x + x^2 }{1+ x +x^2}$ is $\frac{1}{3}$
Hence, the correct answer is option (D).
Answer:
The given function is
$f(x) = [ x ( x-1)+ 1 ] ^{\frac13 }$
$f^{'}(x) = \frac{1}{3}.[(x-1)+x].\frac{1}{[x(x-1)+1]^\frac{2}{3}} = \frac{2x-1}{3[x(x-1)+1]^\frac{2}{3}}$
$f^{'}(x) = 0$
$ ⇒\frac{2x-1}{3[x(x-1)+1]^\frac{2}{3}} = 0$
$⇒ x =\frac{1}{2}$
Hence, $x = \frac12$ is the critical point s0 we need to check the value at x = $\frac12$ and at the end points of given range, i.e. at x = 1 and x = 0
$f(\frac{1}{2}) = [ \frac{1}{2} ( \frac{1}{2}-1)+ 1 ] ^{\frac13 } = \left ( \frac{3}{4} \right )^\frac{1}{3}$
$f(0) = [ 0 ( 0-1)+ 1 ] ^{\frac13} = \left ( 1 \right )^\frac{1}{3} = 1$
$f(1) = [ 1 ( 1-1)+ 1 ] ^{\frac13 } = \left ( 1 \right )^\frac{1}{3} = 1$
Hence, by this, we can say that the maximum value of the given function is 1 at x = 0 and x = 1
Hence, the correct answer is option (C).
|
NCERT Application of Derivatives Class 12 Solutions: Miscellaneous Exercise |
Question 1: Show that the function given by $f ( x ) = \frac{\log x}{x}$ has a maximum at x = e.
Answer:
Given function is
$f ( x ) = \frac{\log x}{x}$
$f^{'}(x) = \frac{1}{x}.\frac{1}{x} + log x\frac{-1}{x^2} = \frac{1}{x^2}(1-\log x)$
$f^{'}(x) =0$
$⇒ \frac{1}{x^2}(1-\log x) = 0$
$⇒ \frac{1}{x^2} \neq 0 $
So, $\log x = 1$
$\Rightarrow x = e$
Hence, x = e is the critical point
Now,
$f^{''}(x) = \frac{-2x}{x^3}(1-\log x)+\frac{1}{x^2}(-\frac{1}{x}) = \frac{1}{x^3}(-2x+2x \log x-1)$
$f^{''}(e) = \frac{-1}{e^3} < 0$
Hence, x = e is the point of maxima.
Answer:
It is given that the base of the triangle is b.
and let the side of the triangle be x cm , $\frac{dx}{dt} = -3 $ cm/s
We know that the area of the triangle(A) = $\frac{1}{2}bh$
now, $h = \sqrt{x^2-(\frac{b}{2})^2}$
$A= \frac{1}{2}b \sqrt{x^2-(\frac{b}{2})^2}$
$\frac{dA}{dt}=\frac{dA}{dx}.\frac{dx}{dt}= \frac{1}{2}b\frac{2x}{2\sqrt{x^2-(\frac{b}{2})^2}}.(-3)$
Now, at x = b
$\frac{dA}{dx} = \frac{1}{2}b\frac{2b}{\frac{\sqrt3b}{2}}.(-3)=-\sqrt3b$
Hence, the area decreases when the two equal sides are equal to the base is $\sqrt3b$ cm2/s.
Question 3(i): Find the intervals in which the function f given by $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is increasing
Answer:
Given function is
$f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$
$f^{'}(x) = \frac{(4\cos x - 2-\cos x+x\sin x)(2+\cos x)-(4\sin x - 2x - x\cos x )(-\sin x)}{(2+\cos x)^2}$
$=\frac{4\cos x - \cos^2x}{2+\cos x}$
$f^{'}(x)=0$
$⇒ \frac{4\cos x - \cos^2x}{2+\cos x} =0$
$ ⇒\cos x(4-\cos x) = 0$
$ ⇒\cos x = 0$ and $ \cos x =4$
But $\cos x \neq 4$
So,
$\cos x = 0$
$ x = \frac{\pi}{2}$ and $ \frac{3\pi}{2}$
Now three ranges are there $\left ( 0,\frac{\pi}{2} \right ),\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ) $ and $ \left ( \frac{3\pi}{2},2\pi \right )$
In interval $\left ( 0,\frac{\pi}{2} \right ) $ and $ \left ( \frac{3\pi}{2},2\pi \right )$ , $f^{'}(x) > 0$
Hence, the given function $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is increasing in the interval $\left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$
in interval $,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ), f^{'}(x) < 0$ so function is decreasing in this interval.
Question 3(ii): Find the intervals in which the function f given by f x is equal to $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is decreasing
Answer:
Given function is
$f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$
$f^{'}(x) = \frac{(4\cos x - 2-\cos x+x\sin x)(2+\cos x)-(4\sin x - 2x - x\cos x )(-\sin x)}{(2+\cos x)^2}$
$=\frac{4\cos x - \cos^2x}{2+\cos x}$
$f^{'}(x)=0$
$ \frac{4\cos x - \cos^2x}{2+\cos x} =0$
$ \cos x(4-\cos x) = 0$
$ \cos x = 0 $ and $ \cos x =4$
But $\cos x \neq 4$
So,
$\cos x = 0 \\ x = \frac{\pi}{2}$ and $ \frac{3\pi}{2}$
Now three ranges are there $\left ( 0,\frac{\pi}{2} \right ),\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$
In interval $\left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$ , $f^{'}(x) > 0$
Hence, given function $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is increasing in interval $\left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$
in interval $,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ), f^{'}(x) < 0$
Hence, given function $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is decreasing in interval $,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right )$.
Question 4(i): Find the intervals in which the function f given by $f (x) = x ^3 + \frac{1}{x^3}, x \neq 0$ Increasing
Answer:
Given function is
$f (x) = x ^3 + \frac{1}{x^3}$
$f^{'} (x) = 3x ^2 + \frac{-3x^2}{x^4}\\ f^{'}(x) = 0\\ 3x ^2 + \frac{-3x^2}{x^4} = 0\\ x^4 = 1\\ x = \pm1$
Hence, three intervals are their $(-\infty,-1),(-1,1) \ and (1,\infty)$
In interval $(-\infty,-1) \ and \ (1,\infty) , f^{'})x > 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is increasing in interval $(-\infty,-1) \ and \ (1,\infty)$
In interval (-1,1) , $f^{'}(x)< 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is decreasing in interval (-1,1)
Question 4(ii): Find the intervals in which the function f given by $f ( x) = x ^3 + \frac{1}{x^3} , x \neq 0$ decreasing
Answer:
Given function is
$f (x) = x ^3 + \frac{1}{x^3}$
$f^{'} (x) = 3x ^2 + \frac{-3x^2}{x^4}$
$f^{'}(x) = 0$
$ ⇒3x ^2 + \frac{-3x^2}{x^4} = 0$
$ ⇒x^4 = 1$
$⇒x = \pm1$
Hence, three intervals are their $(-\infty,-1),(-1,1) $ and $(1,\infty)$
In interval $(-\infty,-1)$ and $(1,\infty) , f^{'})x > 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is increasing in interval $(-\infty,-1)$ and $ (1,\infty)$
In interval (-1, 1), $f^{'}(x)< 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is decreasing in interval (-1, 1).
Answer:
Given the equation of the ellipse
$\frac{x ^2 }{a^2}+ \frac{y^2}{b^2 } = 1$
Now, we know that an ellipse is symmetrical about the x and y-axis.
Therefore, let's assume coordinates of A = (-n, m) then,
Now,
Put(-n,m) in equation of ellipse
We will get
$m = \pm \frac{b}{a}.\sqrt{a^2-n^2}$
Therefore, Now
Coordinates of A = $\left ( -n,\frac{b}{a}.\sqrt{a^2-n^2} \right )$
Coordinates of B = $\left ( -n,-\frac{b}{a}.\sqrt{a^2-n^2} \right )$
Now,
Length AB(base) = $2\frac{b}{a}.\sqrt{a^2-n^2}$
And height of triangle ABC = (a+n)
Now,
Area of triangle = $\frac{1}{2}bh$
$A = \frac{1}{2}.\frac{2b}{a}.\sqrt{a^2-n^2}.(a+n)= ab\sqrt{a^2-n^2}+bn\sqrt{a^2-n^2}$
Now,
$\frac{dA}{dn} = \frac{-abn}{\sqrt{a^2-n^2}}+n\sqrt{a^2-n^2}-\frac{bn^2}{\sqrt{a^2-n^2}}$
Now,
$\frac{dA}{dn} =0$
$\frac{-abn}{\sqrt{a^2-n^2}}+n\sqrt{a^2-n^2}-\frac{bn^2}{\sqrt{a^2-n^2}} =0$
$-abn + n(a^2-n^2)-bn^2 = 0$
$ \Rightarrow n = -a,\frac{a}{2}$
but n cannot be zero,
therefore, $n = \frac{a}{2}$
Now, at $n = \frac{a}{2}$
$\frac{d^2A}{dn^2}< 0$
Therefore, $n = \frac{a}{2}$ is the point of maxima
Now,
$b = 2\frac{b}{a}.\sqrt{a^2- (\frac{a}{2})^2}= \sqrt3b$
$h = (a+ n ) = a+ \frac{ a}{2} = \frac{ 3a}{2}$
Now,
Therefore, Area (A) $= \frac{1}{2}bh = \frac{1}{2}\sqrt3 b \frac{3a}{2} = \frac{3\sqrt3ab}{4}$
Answer:
Let l, b, and h be the length, breath and height of the tank.
Then, volume of tank = l X b X h = 8 $m^3$
h = 2m (given)
lb = 4 = $l = \frac{4}{b}$
Now,
area of base of tank = l X b = 4
area of 4 side walls of tank = hl + hl + hb + hb = 2h(l + b)
Total area of tank (A) = 4 + 2h(l + b)
$A(b) = 4 + 2h(\frac{4}{b}+b)$
$A^{'}(b) = 2h(\frac{-4}{b^2}+1)$
$A^{'}(b)=0$
$ ⇒2h(\frac{-4}{b^2}+1) = 0$
$⇒ b^2= 4$
$⇒ b = 2$
Now,
$A^{''}(b) = 2h(\frac{-4\times-2b}{b^3})$
$A^{''}(2) = 8 > 0$
Hence, b = 2 is the point of minima
$l = \frac{4}{b} = \frac{4}{2} = 2$
So, l = 2 , b = 2 and h = 2 m
Area of base = l × B = 2 × 2 = 4 m2
The building of the tank costs Rs 70 per square meter for the base
Therefore, for 4 m2, Rs = 4 × 70 = Rs. 280
Area of 4 side walls = 2h(l + b)
= 2 × 2(2 + 2) = 16 m2
The building of the tank costs Rs 45 per square metre for sides
Therefore, for 16 m2, Rs = 16 × 45 = Rs. 720
Therefore, total cost for making the tank is = 720 + 280 = Rs. 1000
Answer:
It is given that the sum of the perimeters of a circle and a square is
$k = 2\pi r + 4a = k$
$\Rightarrow a = \frac{k - 2\pi r}{4}$
Let the sum of the area of a circle and square(A) = $\pi r^2 + a^2$
$A = \pi r^2 + (\frac{k-2\pi r}{4})^2$
$A^{'}(r) = 2\pi r + 2(\frac{k-2\pi r}{16})(- 2\pi)$
$ A^{'}(r) = 0$
$⇒ 2\pi (\frac{8r-k-2\pi r}{8}) = 0$
$⇒ r = \frac{k}{8-2\pi}$
Now,
$A^{''}(r) = 2\pi (\frac{8-2\pi }{8}) = 0$
$⇒A^{''}(\frac{k}{8-2\pi}) > 0$
Hence, $r= \frac{k}{8-2\pi}$ is the point of minima
$a = \frac{k-2\pi r}{4} = \frac{k-2\pi \frac{k}{8-2\pi}}{4}=2 \frac{k}{8-2\pi} = 2r$
Hence, it is proved that the sum of their areas is the least when the side of the square is double the radius of the circle.
Answer:
Let l and bare the length and breadth of rectangle respectively and r will be the radius of circle
$(r = \frac{l}{2})$
The total perimeter of the window = perimeter of the rectangle + perimeter of the semicircle
= $l+2b + \pi \frac{l}{2}$
$l+2b + \pi \frac{l}{2} = 10$
$⇒ l = \frac{2(10-2b)}{2+\pi}$
Area of window id given by (A) = $lb + \frac{\pi}{2}\left ( \frac{l}{2} \right )^2$
$= \frac{2(10-2b)}{2+\pi}b + \frac{\pi}{2}\left ( \frac{10-2b}{2+\pi} \right )^2\\$
$A^{'}(b) = \frac{20-8b}{2+\pi}+\frac{\pi}{2}.2(\frac{10-2b}{2+\pi}).\frac{(-2)}{2+\pi}$
$= \frac{20-8b}{2+\pi}-2\pi(\frac{10-2b}{(2+\pi)^2})$
$ A^{'}(b) = 0$
$⇒ \frac{20-8b}{2+\pi}=2\pi(\frac{10-2b}{(2+\pi)^2})$
$⇒ 40 + 20\pi -16b -8\pi b = 20\pi - 4\pi b$
$⇒40 = 4b(\pi+4)$
$⇒b = \frac{10}{\pi+4}$
Now,
$A^{''}(b) = \frac{-8}{2+\pi}+\frac{4\pi}{(2+\pi)^2} = \frac{-16-8\pi+4\pi}{(2+\pi)^2} = \frac{-16-4\pi}{(2+\pi)^2} $
$⇒A^{''}(\frac{10}{\pi+4}) < 0$
Hence, $b=\frac52$ is the point of maxima.
$l = \frac{2(10-2b)}{2+\pi} = \frac{2(10-2.\frac{10}{4+\pi})}{2+\pi} = \frac{20}{4+\pi}$
$r= \frac{l}{2}= \frac{20}{2(4+\pi)}=\frac{10}{4+\pi}$
Hence, these are the dimensions of the window to admit maximum light through the whole opening.
Answer:
It is given that
A point on the hypotenuse of a triangle is at a distance a and b from the sides of the triangle.
Let the angle between AC and BC be $\theta$.
So, the angle between AD and ED is also $\theta$
Now,
CD = $b \operatorname{ cosec}\theta$
And
AD = $a \sec\theta$
AC = H = AD + CD = $a \sec\theta$ + $b \operatorname{ cosec}\theta$
$\frac{dH}{d\theta} = a \sec\theta\tan\theta - b\cot\theta \operatorname{ cosec} \theta$
$ \frac{dH}{d\theta} = 0$
$a \sec\theta\tan\theta - b\cot\theta \operatorname{ cosec} \theta =0$
$⇒ a \sec\theta\tan\theta = b\cot\theta \operatorname{ cosec} \theta$
$⇒ a\sin^3\theta = b\cos^3\theta$
$\tan^3\theta = \frac{b}{a} \\ \tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}$
Now,
$\frac{d^2H}{d\theta^2} > 0$
When $\tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}$
Hence, $\tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}$ is the point of minima.
$\sec \theta = \frac{a\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{a^\frac{1}{3}}$ and $\operatorname{ cosec} \theta = \frac{b\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{b^\frac{1}{3}}$
AC = $\frac{a\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{a^\frac{1}{3}} +$ $\frac{b\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{b^\frac{1}{3}}$ = $(a^\frac{2}{3}+b^\frac{2}{3})^\frac{3}{2}$
Hence, it is proved.
Answer:
The given function is
$f(x) = (x-2)^4(x+1)^3$
$f^{'}(x) = 4(x-2)^3(x+1)^3 + 3(x+1)^2(x-2)^4$
$ f^{'}(x)= 0$
$ 4(x-2)^3(x+1)^3 + 3(x+1)^2(x-2)^4=0$
$⇒ (x-2)^3(x+1)^2(4(x+1) + 3(x-2))=0$
$ x = 2 , x = -1 $ and $ x = \frac{2}{7}$
Now, for value x close to $\frac{2}{7}$ and to the left of $\frac{2}{7}$,
$f^{'}(x) > 0$, and for value close to $\frac{2}{7}$ and to the right of $\frac{2}{7}$ $f^{'}(x) < 0$
Thus, point x = $\frac{2}{7}$ is the point of maxima.
Now, for value x close to 2 and to the right of 2, $f^{'}(x) > 0$, and for value x close to 2 and to the left of 2, $f^{'}(x) < 0$.
Thus, point x = 2 is the point of minimum.
There is no change in the sign when the value of x is -1.
Thus, x = -1 is the point of inflexion.
Answer:
The given function is
$f (x) = \cos ^2 x + \sin x$
$f^{'} (x) = 2\cos x(-\sin x) + \cos x$
$ f^{'}(x) = 0$
$ ⇒ -2\cos x\sin x + \cos x=0$
$⇒ \cos x(1-2\sin x) = 0$ either $ \cos x = 0$ and $\sin x = \frac{1}{2}$
$⇒ x = \frac{\pi}{2}$ and $ x = \frac{\pi}{6}$ as $\ x \ \epsilon [0,\pi]$
Now,
$f^{''} (x) = -2(-\sin x)\sin x - 2\cos x\cos x + (-\sin x) $
$⇒ f^{''}(x)= 2\sin^2x - 2\cos^2x - \sin x$
$⇒ f^{''}(\frac{\pi}{6}) = \frac{-3}{2} < 0$
Hence, the point $x = \frac{\pi}{6}$ is the point of maxima and the maximum value is
$f (\frac{\pi}{6}) = \cos ^2 \frac{\pi}{6} + \sin \frac{\pi}{6} = \frac{3}{4}+\frac{1}{2} = \frac{5}{4}$
And
$f^{''}(\frac{\pi}{2}) = 1 > 0$
Hence, the point $x = \frac{\pi}{2}$ is the point of minima and the minimum value is
$f (\frac{\pi}{2}) = \cos ^2 \frac{\pi}{2} + \sin \frac{\pi}{2} = 0 + 1 = 1$
Answer:
The volume of a cone (V) = $\frac{1}{3}\pi R^2h$
The volume of the sphere with radius r = $\frac{4}{3}\pi r^3$
By Pythagoras' theorem in $\Delta ADC$, we can say that
$OD^2 = r^2 - R^2 $
$ OD = \sqrt{r^2 - R^2}$
$ h = AD = r + OD = r + \sqrt{r^2 - R^2}$
$V = \frac{1}{3}\pi R^2 (r + \sqrt{r^2+R^2})$
$⇒ V = \frac{1}{3}\pi R^2r + \frac{1}{3}\pi R^2 \sqrt{r^2+R^2}$
$⇒V=\frac{1}{3}\pi R^2 (r + \sqrt{r^2-R^2})$
$V^{'}(R)= \frac{2}{3}\pi Rr + \frac{2}{3}\pi R \sqrt{r^2-R^2}+\frac{1}{3}\pi R^2.\frac{-2R}{2\sqrt{r^2-R^2}}$
Also, $ V^{'}(R) = 0$
$ ⇒\frac{1}{3}\pi R \left ( 2r + 2\sqrt{r^2-R^2} - \frac{R^2}{\sqrt{r^2-R^2}} \right ) = 0$
$ ⇒\frac{1}{3}\pi R \left ( \frac{2r\sqrt{r^2-R^2} + 2r^2-2R^2 -R^2}{\sqrt{r^2-R^2}} \right ) = 0$
$R \neq 0$
So, $2r\sqrt{r^2-R^2} = 3R^2 - 2r^2$
Squaring both sides, we get,
$⇒4r^4-4r^2R^2 = 9R^4 + 4r^4 - 12R^2r^2$
$⇒ 9R^4-8R^2r^2 = 0$
$⇒ R^2(9R^2-8r^2) = 0$
$ R\neq 0 $
So, $9R^2 = 8r^2$
$⇒R = \frac{2\sqrt2r}{3}$
Now,
$V^{''}(R)= \frac{2}{3}\pi r + \frac{2}{3}\pi \sqrt{r^2-R^2}+\frac{2}{3}\pi R.\frac{-2R}{2\sqrt{r^2-R^2}}-\frac{3\pi R^2}{\sqrt{r^2-R^2}} - \frac{(-1)(-2R)}{(r^2+R^2)\frac{3}{2}}$
$ ⇒V^{''}(\frac{2\sqrt2r}{3}) < 0$
Hence, the point $R = \frac{2\sqrt2r}{3}$ is the point of maxima.
$h = r + \sqrt{r^2-R^2} = r + \sqrt{r^2-\frac{8r^2}{9}} = r + \frac{r}{3} = \frac{4r}{3}$
Hence, the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is $\frac{4r}{3}$.
Answer:
Let's do this question by taking an example.
Suppose
$f(x)= x^3 > 0 , (a.b)$
Now, also
$f{'}(x)= 3x^2 > 0 , (a,b)$
Hence, by this, we can say that f is an increasing function on (a, b).
Answer:
The volume of the cylinder (V) = $\pi r^2 h$
By Pythagoras' theorem in $\Delta OAB$
$OA = \sqrt{R^2-r^2}$
h = 2OA
$h = 2\sqrt{R^2-r^2}$
$V = 2\pi r^2\sqrt{R^2-r^2}$
$V^{'}(r) = 4\pi r\sqrt{R^2-r^2}+2\pi r^2 . \frac{-2r}{2\sqrt{R^2-r^2}}$
$ V^{'}(r) = 0$
$⇒ 4\pi r\sqrt{R^2-r^2}- \frac{2\pi r^3}{\sqrt{R^2-r^2}} = 0$
$ ⇒4\pi r (R^2-r^2 ) - 2\pi r^3 = 0$
$⇒ 6\pi r^3 = 4\pi rR^2$
$⇒r =\frac{\sqrt6R}{3}$
Now,
$V^{''}(r) = 4\pi \sqrt{R^2-r^2}+4\pi r.\frac{-2r}{2\sqrt{R^2-r^2}}- \frac{6\pi r^2}{\sqrt{R^2-r^2}}.\frac{(-1)-2r}{2(R^2-r^2)\frac{3}{2}}$
$⇒V^{''}(\frac{\sqrt6R}{3}) < 0$
Hence, the point $r = \frac{\sqrt6R}{3}$ is the point of maxima
$h = 2\sqrt{R^2-r^2} = 2\sqrt{R^2 - \frac{2R^2}{3}} =\frac{2R}{\sqrt3}$
Hence, the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is $\frac{2 R }{\sqrt 3 }$
And the maximum volume is
$V = \pi r^2 h = \pi \frac{2R^2}{3}.\frac{2R}{\sqrt3} = \frac{4\pi R^3}{3\sqrt3}$
Answer:
Let's take the radius and height of the cylinder = r and h, respectively.
Let's take the radius and height of the cone = R and h, respectively.
Volume of cylinder = $\pi r^2 h'$
Volume of cone = $\frac{1}{3}\pi R^2 h$
Now, we have
$R = h\tan a$
Now, since $\Delta AOG$ and $ \Delta CEG$ are similar.
$\frac{OA}{OG} = \frac{CE}{EG}$
$\frac{h}{R} = \frac{h'}{R-r}$
$h'=\frac{h(R-r)}{R}$
$h'=\frac{h(h\tan a-r)}{h\tan a} = \frac{h\tan a- r}{\tan a}$
Now,
$V = \pi r^ 2 h' = \pi r^2 .\frac{h\tan a-r}{\tan a} = \pi r^2 h - \frac{\pi r^3}{\tan a}$
Now,
$\frac{dV}{dr}= 2\pi rh- \frac{3\pi r^2}{\tan a} $
$ \frac{dV}{dr}=0$
$ ⇒2\pi rh- \frac{3\pi r^2}{\tan a} = 0$
$⇒ 2\pi rh = \frac{3\pi r^2}{\tan a}$
$⇒r = \frac{2h\tan a}{3}$
Now,
$\frac{d^2V}{dr^2}= 2\pi h- \frac{6\pi r}{\tan a}$
at $r = \frac{2h\tan a}{3}$
$\frac{d^2V}{dr^2} = 2\pi h- 4\pi h < 0$
Hence, $r = \frac{2h\tan a}{3}$ is the point of maxima.
$h' = \frac{h\tan a-r}{\tan a} = \frac{h\tan a- \frac{2h\tan a}{3}}{\tan a}= \frac{1}{3}h$
Hence, it is proved.
Now, Volume (V) at $h' = \frac{1}{3}h$ and $r = \frac{2h\tan a}{3}$ is
$V = \pi r^2 h' = \pi \left ( \frac{2h\tan a}{3} \right )^2.\frac{h}{3}= \frac{4}{27}.\pi h^3\tan^2 a$
Hence, it is proved.
Answer:
It is given that
$\frac{dV}{dt} = 314$ m3/h
Volume of cylinder (V) = $\pi r^2 h = 100\pi h \ \ \ \ \ \ \ \ \ \ \ (\because r = 10 m)$
$\frac{dV}{dt} = 100\pi \frac{dh}{dt}$
$⇒314 = 100\pi \frac{dh}{dt}$
$⇒ \frac{dh}{dt} = \frac{3.14}{\pi} = 1$ m/h
Hence, the correct answer is option (A).
Also, read,
Take Aakash iACST and get instant scholarship on coaching programs.
Question:
Show that the function $f(x)=\frac{x}{3}+\frac{3}{x}$ decreases in the intervals $(-3,0) \cup(0,3)$.
Solution:
$
\begin{aligned}
& f(x)=\frac{x}{3}+\frac{3}{x} \\
& f^{\prime}(x)=\frac{1}{3}-\frac{3}{x^2}
\end{aligned}
$
For $f(x)$ decreases
$
\begin{aligned}
& \frac{1}{3}-\frac{3}{x^2}<0 \\
& \frac{1}{3}<\frac{3}{x^2} \\
& x^2<9 \\
& x \in(-3,0) \cup(0,3)
\end{aligned}
$
Hence, the given statement is proved.
Here is the list of important topics that are covered in Class 12 Maths Chapter 6 Solutions:
Given below are some important formulas that are used in the Application of Derivatives Class 12 NCERT Solution:
Definition of Derivatives: Derivatives measure the rate of change of quantities.
Rate of Change of a Quantity:
The derivative is used to find the rate of change of one quantity with respect to another. For a function y = f(x), the average rate of change in the interval [a, a+h] is:
$\frac{(f(a + h) - f(a)) } h$
Approximation:
Derivatives help find approximate values of functions. Newton's linear approximation method involves finding the equation of the tangent line.
Linear approximation equation: L(x) = f(a) + f'(a)(x - a)
Tangents and Normals:
A tangent to a curve touches it at a single point and has a slope equal to the derivative at that point.
Slope of tangent (m) = f'(x)
The equation of the tangent line is found using: m = $\frac{y_2-y_1}{x_2-x_1}$
The normal to a curve is perpendicular to the tangent.
The slope of normal (n) = $-\frac{1}{f’(x)}$
The equation of the normal line is found using: $-\frac 1m=\frac{y_2-y_1}{x_2-x_1}$
Maxima, Minima, and Points of Inflexion:
Maxima and minima are peaks and valleys of a curve. The point of inflexion marks a change in the curve's nature (convex to concave or vice versa).
To find maxima, minima, and points of inflexion, use the first derivative test:
Increasing and Decreasing Functions:
An increasing function tends to reach the upper corner of the x-y plane, while a decreasing function tends to reach the lower corner.
For a differentiable function f(x) in the interval (a, b):
If f(x1) > f(x2) when x1 < x2, it's strictly decreasing.
Here are some approaches that students can follow to solve these Class 12 Maths NCERT Chapter 6 problems smoothly.
Here is a comparison list of the concepts in Application of Derivatives that are covered in JEE and NCERT, to help students understand what extra they need to study beyond the NCERT for JEE:
|
Concept Name |
JEE |
NCERT |
|
✅ |
✅ | |
|
✅ |
✅ | |
|
✅ |
✅ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ |
✅ | |
|
✅ | ❌ | |
|
✅ |
✅ | |
|
✅ |
✅ | |
|
✅ |
✅ | |
|
✅ | ❌ | |
|
Application of Extremum in Plane Geometry and Solid geometry |
✅ | ❌ |
|
Continuity and Discontinuity obtained by Algebraic Operations |
✅ | ❌ |
Given below is the chapter-wise list of the NCERT Class 12 Maths solutions with their respective links:
Also, read,
Students can use the following links to check the solutions to science subjects like Physics, Chemistry, & Biology questions.
These are links to the solutions of other classes, which students can check to revise and strengthen those concepts.
Students should always check the latest NCERT syllabus before planning their study routine. Also, some reference books should be read after completing the textbook exercises. The following links will be very helpful for students for these purposes.
Frequently Asked Questions (FAQs)
There are 4 exercises, including the miscellaneous exercise in Class 12 Maths NCERT Chapter 6, Application of Derivatives.
Maxima & minima problems are very common in the exam, and knowing some tricks would help students to get maximum numbers from these questions. Here are some important tricks to solve these questions.
If the first derivative, f'(x) > 0 in an interval, then the function is increasing. And if f'(x) < 0 in an interval, then the function is decreasing.
The key topics covered in Class 12 Maths NCERT Chapter 6, Application of Derivatives are:
Rolle's theorem states that if a function f is continuous on [a, b], differentiable on (a, b), and f(a) = f(b)
Then, there exists some c that belongs to (a, b), such that f'(c) = 0
This theorem confirms a point where the slope or derivative is zero.
On Question asked by student community
Hello
Yes, if you’re not satisfied with your marks even after the improvement exam, many education boards allow you to reappear as a private candidate next year to improve your scores. This means you can register independently, study at your own pace, and take the exams without attending regular classes. It’s a good option to improve your results and open up more opportunities for higher studies or careers. Just make sure to check the specific rules and deadlines of your education board so you don’t miss the registration window. Keep your focus, and you will do better next time.
Hello Aspirant,
Yes, in the case that you appeared for the 2025 improvement exam and your roll number is different from what was on the previous year’s marksheet, the board will usually release a new migration certificate. This is because the migration certificate will reflect the most recent exam details, roll number and passing year. You can apply to get it from your board using the process prescribed by them either online or through your school/college.
Yes, if you miss the 1st CBSE exam due to valid reasons, then you can appear for the 2nd CBSE compartment exam.
From the academic year 2026, the board will conduct the CBSE 10th exam twice a year, while the CBSE 12th exam will be held once, as per usual. For class 10th, the second phase exam will act as the supplementary exam. Check out information on w hen the CBSE first exam 2026 will be conducted and changes in 2026 CBSE Board exam by clicking on the link .
If you want to change your stream to humanities after getting a compartment in one subject in the CBSE 12th Board Exam , you actually have limited options to qualify for your board exams. You can prepare effectively and appear in the compartment examination for mathematics again. If you do not wish to continue with the current stream, you can take readmission in the Humanities stream and start from Class 11th again, and continue studying for two more years to qualify for the 12th examination.
The GUJCET Merit List is prepared based on the Class 12th marks and GUJCET marks received by the students. CBSE students who are not from the Gujarat board can definitely compete with GSEB students, as their eligibility is decided based on the combined marks scored by them in GUJCET and the 12th board. The weightage of the GUJCET score is 40% and the weightage of the class 12 scores is 60%.
Take Aakash iACST and get instant scholarship on coaching programs.
This ebook serves as a valuable study guide for NEET 2025 exam.
This e-book offers NEET PYQ and serves as an indispensable NEET study material.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
As per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE