NCERT Solutions for Class 11 Physics Chapter 3 Motion in a Plane
Have you ever thought of why a football will go in a curvy direction through the air or why a car will go through a safe turn on a curvy road? Class 11 Physics Chapter 3 Motion in a Plane explains these everyday phenomena. This chapter aids students in the explanation of two-dimensional motion with the concepts of projectile motion, uniform circular motion, and adding vectors. The NCERT Solutions of Class 11 Physics Chapter 3 offer solutions to questions in the textbook in a step-by-step manner, and thus, the students can practice well and get a good result in examinations.
This Story also Contains
- Class 11 Physics Chapter 3 - Motion in a Plane Question Answers: Download PDF
- Motion in a Plane NCERT Solutions: Exercise Questions
- Motion in a Plane NCERT Solutions: Additional Questions
- Motion in a Plane NCERT Solutions: Higher Order Thinking Skills (HOTS) Questions
- Class 11 Physics Chapter 3 - Motion in a Plane: Topics
- NCERT Solutions for Class 11 Physics Chapter 3 - Motion in a Plane: Important Formulae
- Approach to Solve Questions of Class 11 Physics Chapter 3 - Motion in a Plane
- How Can NCERT Solutions for Class 11 Physics Chapter 3 Motion in a Plane Help in Exam Preparation?
- What Extra Should Students Study Beyond NCERT for JEE?
- NCERT Solutions for Class 11 Physics Chapter Wise

These NCERT Solutions for Class 11 Physics Chapter 3 - Motion in a Plane are formulated based on the most recent CBSE syllabus and include the most significant concepts like vectors and the use of vector algebra in motion. Exercise problem solving, in-text questions, and other practice questions help students to establish a great conceptual clarity and analytical thinking. The NCERT Solutions for Class 11 Physics Chapter 3 - Motion in a Plane also help students in the preparation of such competitive exams as JEE, NEET, and Olympiads because they are also provided with a sharp understanding and problem-solving ability of numerical problems. This chapter extends Chapter 2 (Motion in a Straight Line) by introducing motion in two dimensions and therefore forms a very important building block to further Physics concepts. By using NCERT Solutions of Motion in a plane, students are able not only to enhance their preparation for the examination but also to develop confidence in using Physics in real-life circumstances.
Class 11 Physics Chapter 3 - Motion in a Plane Question Answers: Download PDF
Download Motion in a Plane NCERT Solutions PDF written by subject experts in simple and clear language to help you understand the chapter better and revise quickly. This PDF includes all the exercise questions of Chapter 3 and also contains the additional questions that were present in the NCERT before but have now been removed from the textbook.
Motion in a Plane NCERT Solutions: Exercise Questions
Class 11 Physics Chapter 3 - Motion in a Plane Exercise Solutions help students master the concepts of Motion in a Plane, including vectors, projectile motion, and relative velocity. These class 11 physics chapter 3 Motion in a plane question answers provide clear, step-by-step answers to textbook questions, making problem-solving easier and strengthening exam preparation.
Q. 3.1 State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity
Answer:- Volume is a scalar quantity since it has only magnitude without any direction.
- Mass is a scalar quantity because it is specified only by magnitude.
- Speed is specified only by its magnitude, not by its direction, so it is a scalar quantity.
- Acceleration is a vector quantity as it has both magnitude and direction associated.
- Density is a scalar quantity as it is specified only by its magnitude.
- The number of moles is a scalar quantity as it is specified only by its magnitude.
- Velocity is a vector quantity as it has both magnitude and direction.
- Angular frequency is a scalar quantity as it is specified only by its magnitude.
- Displacement is a vector quantity since it has both magnitude and direction.
- Angular velocity is a vector quantity as it has both magnitude and direction.
force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity
Answer:
The two scalar quantities are work and current, as these two do not follow the laws of vector addition.
Temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge
Answer:
Among all, impulse is the only vector quantity as it is the product of two vector quantities (force and time). Also, it has an associated direction.
(a) adding any two scalars, (b) adding a scalar to a vector of the same dimensions, (c) multiplying any vector by any scalar, (d) multiplying any two scalars, (e) adding any two vectors, (f) adding a component of a vector to the same vector
Answer:
- (a) Adding two scalars is meaningful if both have the same unit or represent the same physical quantity.
- (b) Adding a scalar to a vector of the same dimensions is meaningless because a vector has direction, while a scalar does not.
- (c) Multiplying a vector by a scalar is meaningful, as it changes only the magnitude of the vector while keeping its direction unchanged.
- (d) Multiplying two scalars is valid and meaningful without any condition. The resulting scalar may represent a different physical quantity (units get multiplied).
- (e) Adding two vectors is meaningful only if they represent the same physical quantity, allowing their magnitudes and directions to be combined appropriately.
- (f) Adding a component of a vector to the same vector is meaningful as it is a case of valid vector addition, leading to a new vector with increased magnitude in the same direction.
(a) The magnitude of a vector is always a scalar,
(b) Each component of a vector is always a scalar,
(c) The total path length is always equal to the magnitude of the displacement vector of a particle.
(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater than or equal to the magnitude of the average velocity of the particle over the same interval of time,
(e) Three vectors not lying in a plane can never add up to give a null vector.
Answer:
- (a) True: The magnitude of a vector has no direction, so it is always a scalar.
- (b) False: Each component of a vector is itself a vector, as it retains directional properties.
- (c) False: Total path length equals the magnitude of displacement only in straight-line motion. In general, path length is ≥ displacement.
- (d) True: Average speed is total path length/time, which is ≥ average velocity (displacement/time).
- (e) True: Three vectors not lying in the same plane cannot cancel each other out, hence cannot give a null vector.
Q. 3.6 (a) Establish the following vector inequalities geometrically or otherwise:
Inequality: $|\vec{a} + \vec{b}|$ ≤ $|\vec{a}| + |\vec{b}|$
Answer:
Consider the image below:
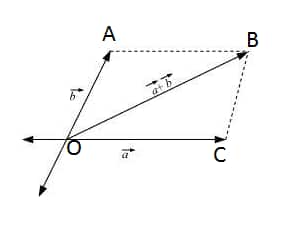
In triangle OCB:
OB < OC + BC ⟹ $|\vec{a} + \vec{b}|$ < $\vec{|a|} + \vec{|b|}$ ..........(i)
If $\vec{a}$ and $\vec{b}$ are in a straight line:
$|\vec{a} + \vec{b}|$ = $|\vec{a}| + |\vec{b}|$ ..........(ii)
Conclusion: From (i) and (ii), $|\vec{a} + \vec{b}|$ ≤ $|\vec{a}| + |\vec{b}|$
Q. 3.6 (b) Establish the following vector inequalities geometrically or otherwise:
Inequality: $|\vec{a} + \vec{b}|$ ≥ $|\vec{a}| + |\vec{b}|$
Answer:
Refer to the same image above.
In triangle OCB:
OB + BC > OC ⟹ OB > |OC − BC|
Therefore, $|\vec{a} + \vec{b}|$ > $|\vec{a}| + |\vec{b}|$ ..........(i)
If vectors a and b are opposite in a straight line:
$|\vec{a} + \vec{b}|$ = $||\vec{a}| − |\vec{b}||$ ..........(ii)
Conclusion: From (i) and (ii), $|\vec{a} + \vec{b}|$ ≥ $||\vec{a}| − |\vec{b}||$
Q. 3.6 (c) Establish the following vector inequalities geometrically or otherwise:
Inequality: $|\vec{a} - \vec{b}|$ ≤ $|\vec{a}| + |\vec{b}|$
Answer:
Refer to the image below:
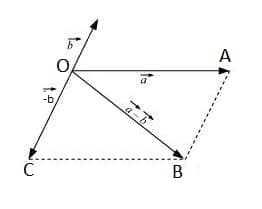
In triangle OAB:
OB < OA + AB ⟹ $|\vec{a} − \vec{b}|$ < $|\vec{a}| + |\vec{b}|$ ..........(i)
If vectors a and b are along the same line:
$|\vec{a} − \vec{b}|$ = $|\vec{a}| + |\vec{b}|$ ..........(ii)
Conclusion: From (i) and (ii), $|\vec{a}-\vec{b}|=|\vec{a}|+|\vec{b}|$
Q. 3.7 Given $\vec{a} + \vec{b} + \vec{c} + \vec{d} = 0, which of the following statements are correct:
(a) $\vec{a}, \vec{b}, \vec{c}, and \ \vec{d}$ must each be a null vector,
(b) The magnitude of $(\vec{a} +\vec{c})$ equals the magnitude of $(\vec{ b} +\vec{d})$,
(c) The magnitude of a can never be greater than the sum of the magnitudes of $\vec{b},\vec{c}, and\ \vec{d}$,
(d) $\vec{b} + \vec{c}$ must lie in the plane of $\vec{a} \ and \ \vec{d}$ if $\vec{a} \ and \ \vec{d}$ are not collinear, and in the line of $\vec{a} \ and \ \vec{d}$, if they are collinear?
Answer:
(a) Incorrect: - Sum of three vectors in a plane can be zero. So it is not a necessary condition that all of $\vec{a}$, $\vec{b}$, $\vec{c}$, $\vec{d}$ should be null vectors.
(b) Correct : We are given that $\vec{a} + \vec{b} + \vec{c} + \vec{d} = 0$
So, $\vec{a} + \vec{b} = - (\vec{c} + \vec{d})$
Thus magnitude of $\vec{a} + \vec{c}$ is equal to the $\vec{c}+\vec{d}.$
(c) Correct :- We have $\vec{a} + \vec{b} + \vec{c} + \vec{d} = 0$
$ \vec{b} + \vec{c} + \vec{d} = -\vec{a}$
So clearly, the magnitude of a cannot be greater than the sum of the other three vectors.
(d) Correct: - Sum of three vectors is zero if they are coplanar.
Thus, $\vec{a} + \vec{b} + \vec{c} + \vec{d} = 0$
or $\vec{a} + (\vec{b} + \vec{c}) + \vec{d} = 0$
Hence $(\vec{b}+\vec{c})$ must be coplaner with $\vec{a} \ and \ \vec{d}$
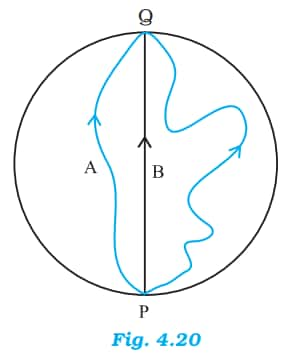
Answer:
The displacement vector is defined as the shortest distance between two points which a particle has covered.
In this case, the shortest distance between these points is the diameter of the circular ice ground.
Thus, Displacement = 400 m.
Girl B had travelled along the diameter, so the path travelled by her is equal to the displacement.
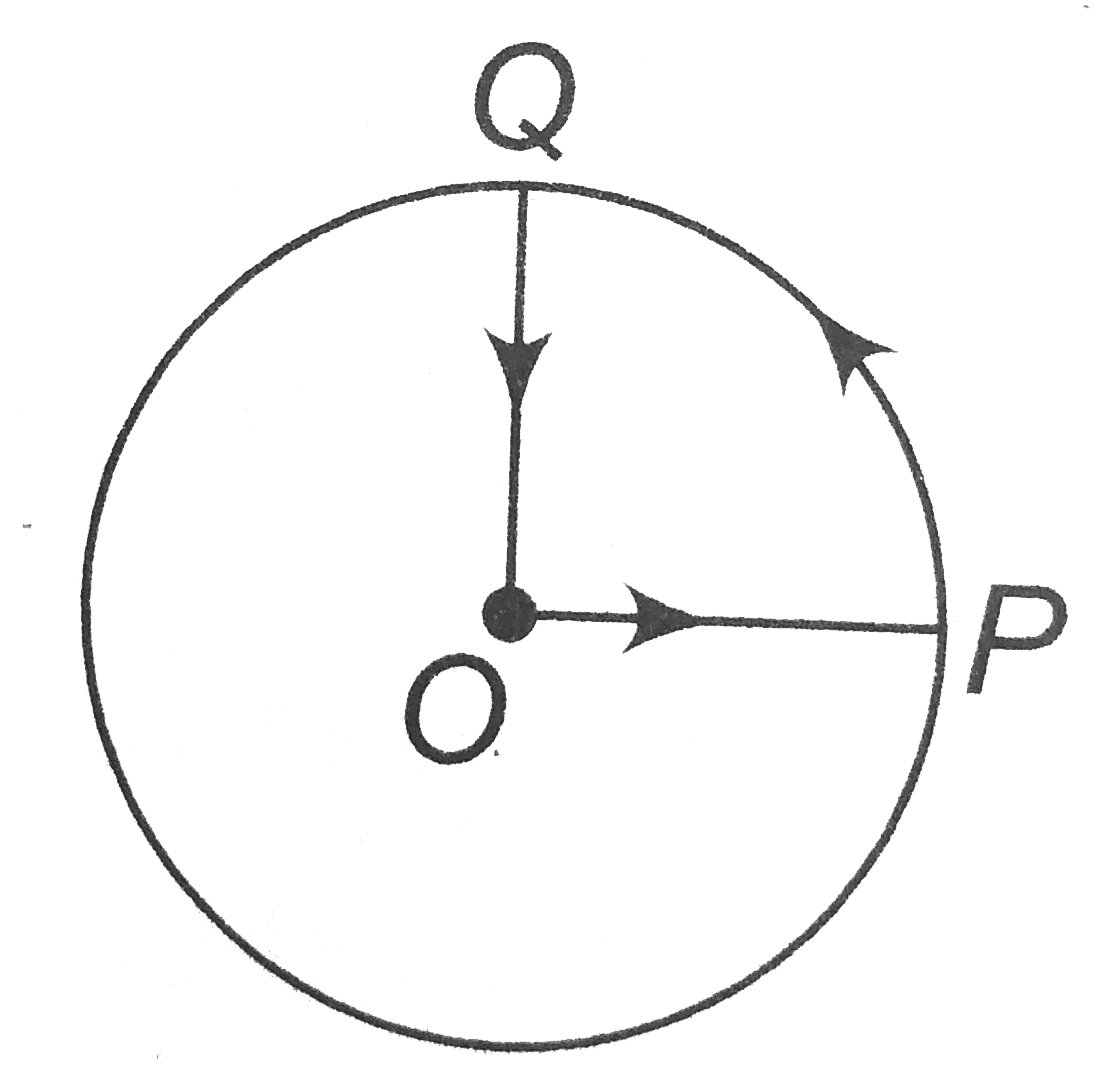
Answer:
The net displacement, in this case, will be zero because the initial and final positions are the same.
Net displacement = Final position - Initial position

Answer:
(b) Average velocity is defined as the net displacement per unit time. Since we have the net displacement to be zero, the average velocity will also be zero.
$Avg.\ Velocity\ =\ \frac{Net\ displacement}{Time\ taken}$

Answer:
(c) For finding the average speed, we need to calculate the total path travelled.
Total path = OP + arc PQ + OQ
$= 1+ \frac{1}{4}(2\pi \times1)+ 1$
$= 3.57\ Km$
$Time\ taken\ in\ hour\ = \frac{1}{6}$
So the average speed is :
$= \frac{3.57}{\frac{1}{6}}\ =\ 21.42\ Km/h$
Answer:
The track is shown in the figure given below:-
Let us assume that the trip starts at point A.
The third turn will be taken at D.
So displacement will be = Distance AD = 500 + 500 = 1000 m
Total path covered = AB + BC + CD = 500 + 500 + 500 = 1500 m
The sixth turn is at A.
So the displacement will be zero
and total path covered will be = 6 (500) = 3000 m
The eighth turn will be at C.
So the displacement = AC
$AC =\ \sqrt{AB^2\ +\ BC ^2\ +\ 2(AB)(BC) \cos 60^{\circ}}$
or $AC=\ \sqrt{(500)^2\ +\ (500) ^2\ +\ 2(500)(500) \cos 60^{\circ}}$
$AC=\ 866.03\ m$
And the total distance covered = 3000 + 1000 = 4000 m=4Km
Answer:
(a) Avg. speed of taxi is given by:-
$=\ \frac{Total\ path\ travelled }{Total\ time\ taken}$
$=\ \frac{23\ Km}{\frac{28}{60}\ h}$
$=\ 49.29\ Km/h$
Answer:
Total displacement = 10 Km
Total time taken in hours :
$=\ \frac{28}{60}\ hr$
Avg. velocity :
$=\ \frac{10}{\frac{28}{60}}\ hr$
$=\ 21.43\ Km/h$
It can be clearly seen that the average. speed and avg. velocity is not the same.
Answer:
It is known that the maximum height reached by a particle in projectile motion is given by :
$h\ =\ \frac{u^2sin^2\theta }{2g}$
Putting the given values in the above equation :
$25\ =\ \frac{40^2sin^2\theta }{2\times9.8}$
So, we get
$\sin \theta \ =\ 0.5534$ and $\theta \ =\ 33.60^{\circ}$
Now the horizontal range can be found from :
$R\ =\ \frac{u^2 \sin 2\theta }{g}$
or $R=\ \frac{40^2 \sin (2\times 33.6 )}{9.8}$
or $R=\ 150.53\ m$
Answer:
We are given the range of projectile motion.
$R\ =\ \frac{u^2\ \sin 2\theta }{g}$
Substituting values :
$100\ =\ \frac{u^2\ \sin 90^{\circ} }{g}$
So, $\frac{u^2 }{g}\ =\ 100$
Now, since deceleration is also acting on the ball in the downward direction :
$v^2\ -\ u^2\ =\ -2gh$
Since the final velocity is 0, so maximum height is given by :
$H\ =\ \frac{u^2}{2g}$
or $H\ =\ 50\ m$
Answer:
Frequency is given by :
$Frequency\ =\ \frac{No.\ of\ revolutions}{Total\ time\ taken}=\ \frac{14}{25}\ Hz$
And, the angular frequency is given by :
$\omega \ =\ 2 \pi f$
Thus, $\omega=\ 2 \times\ \frac{22}{7}\times\frac{14}{25}$
$\omega=\ \frac{88}{25}\ rad/s$
Hence, the acceleration is given by :
$a\ =\ \omega ^2 r$
or $a=\ \left ( \frac{88}{25} \right ) ^2 \times 0.8$
or $a\ =\ 9.91\ m/s^2$
Answer:
Convert all the physical quantities in SI units.
$Speed\ =\ 900\times \frac{5}{18}\ 250\ m/s$
So the acceleration is given by :
$a\ =\ \frac{v^2}{r}$
$a=\ \frac{(250)^2}{1000}$
$a=\ 62.5\ m/s^2$
The ratio of centripetal acceleration to gravity gives :
$\frac{a}{g}=\ \frac{62.5}{9.8}\ =\ 6.38$
Q. 3.16 (a) Read each statement below carefully and state, with reasons, if it is true or false :
Answer:
False:- Since the net acceleration is not directed only along the radius of the circle. It also has a tangential component.
Q. 3.16 (b) Read each statement below carefully and state, with reasons, if it is true or false :
Answer:
True: - Because the particle moves on the circumference of the circle, at any point, its direction should be tangential in order to move in a circular orbit.
Q. 3.16 (c) Read each statement below carefully and state, with reasons, if it is true or false :
Answer:
True: - In a uniform circular motion, acceleration is radially outward all along the circular path. So in 1 complete revolution, all the vectors are cancelled and the null vector is obtained.
Answer:
(a) We are given the position vector $\vec{r}=3.0t\; \hat{i}-2.0t^{2}\; \hat{j}+4.0\; \hat{k}\; m$
The velocity vector is given by:-
$\vec{v} \ =\ \frac{dr}{dt}$
$\vec{v}\ =\ \frac{d\left ( 3.0t\; \hat{i}-2.0t^{2}\; \hat{j}+4.0\; \hat{k} \right )}{dt}$
or $\vec{v}\ =\ 3\; \hat{i}-4t\; \hat{j}$
Now for acceleration :
$\vec{a} \ =\ \frac{dv}{dt}$
$\vec{a}=\ d(\frac{3\; \hat{i}-4t\; \hat{j})}{dt}$
$\vec{a}=\ -4\; \hat{j}$
Answer:
Put the value of time t = 2 in the velocity vector as given below :
$\vec{v}\ =\ 3\; \hat{i}-4t\; \hat{j}$
or $\vec{v}\ =\ 3\; \hat{i}-4(2)\; \hat{j}$
or $\vec{v}=\ 3\; \hat{i}-8\; \hat{j}$
Thus, the magnitude of velocity is :
$|\vec{v}|=\ \sqrt{3^2\ +\ (-8)^2}\ =\ 8.54\ m/s$
Direction :
$\theta \ =\ \tan^{-1} \frac{8}{3}\ =\ -69.45^{\circ}$
Answer:
We are given the velocity of the particle as $10.0\; \hat{j}\; m/s$.
And the acceleration is given as :
$\left ( 8.0\; \hat{i}+2.0\; \hat{j} \right )m\; s^{-2}$
So, the velocity due to acceleration will be :
$\vec{a}\ =\ \vec{\frac{dv}{dt}}$
So, $\vec{dv}\ =\ \left ( 8.0\ \widehat{i}\ +\ 2.0\ \widehat{j} \right )dt$
By integrating both sides,
or $\vec{v}\ =\ 8.0t\ \widehat{i}\ +\ 2.0t\ \widehat{j}\ +\ u$
Here, u is the initial velocity (at t = 0 sec).
Now,
$\vec{v}\ =\vec{\frac{dr}{dt}}$
or $\vec{dr}\ =\ \left ( 8.0t\ \widehat{i}\ +\ 2.0t\ \widehat{j}\ +\ u \right )dt$
Integrating both sides, we get
$\vec{r}\ =\ 8.0\times \frac{1}{2}t^2\ \widehat{i}\ +\ 2.0\times\frac{1}{2} t^2\ \widehat{j}\ +\ (10t\ ) \widehat{j}$
or $\vec{r}\ =\ 4t^2\ \widehat{i}\ +\ (t^2\ +\ 10t\ ) \widehat{j}$
or $x\widehat{i}\ +\ y\widehat{j}\ =\ 4t^2\ \widehat{i}\ +\ (t^2\ +\ 10t\ ) \widehat{j}$
Comparing coefficients, we get :
$x\ =\ 4t^2$ and $y\ =\ 10t\ +\ t^2$
In the question, we are given x = 16.
So t = 2 sec
and y = 10 (2) + 22 = 24 m.
Answer:
The velocity of the particle is given by :
$\vec{v}\ =\ 8.0t\ \widehat{i}\ +\ 2.0t\ \widehat{j}\ +\ u$
Put t = 2 sec,
So velocity becomes :
$\vec{v}\ =\ 8.0(2)\ \widehat{i}\ +\ 2.0(2)\ \widehat{j}\ +\ 10\widehat{j}$
or $\vec{v}\ =\ 16\ \widehat{i}\ +\ 14\ \widehat{j}$
Now, the magnitude of velocity gives :
$\left ||\vec{ v}| \right |\ =\ \sqrt{16^2\ +\ 14^2}$
$|\vec{v}|=\ \sqrt{256+196}$
$|\vec{v}| =\ 21.26\ m/s$
Answer:
Let A be a vector such that:- $\overrightarrow{A}\ =\ \widehat{i}\ +\ \widehat{j}$
Then the magnitude of vector A is given by : $\left | A \right |\ =\ \sqrt{1^2\ +\ 1^2}\ =\ \sqrt{2}$
Now, let us assume that the angle made between vector A and x -axis is $\Theta$.
Then we have:-
$\theta \ =\ \tan^{-1}\left ( \frac{1}{1} \right )\ =\ 45^{\circ}$
Similarly, let B be a vector such that:- $\overrightarrow{B}\ =\ \widehat{i}\ -\ \widehat{j}$
The magnitude of vector B is : $\left | B\right |\ =\ \sqrt{1^2\ +\ (-1)^2}\ =\ \sqrt{2}$
Let $\alpha$ be the angle between vector B and the x-axis :
$\alpha = \tan^{-1}\left ( \frac{-1}{1} \right ) =-45^{\circ}$
Now consider $\overrightarrow{C}\ =\ 2\widehat{i}\ +\ 3\widehat{j}$ :-
Then the required components of a vector C along the directions of $(\hat{i}+\hat{j})$ are:- $=\ \frac{2+3}{\sqrt{2}}\ =\ \frac{5}{\sqrt{2}}$
and the required components of a vector C along the directions of $(\hat{i}-\hat{j})$ is:- $\frac{2-3}{\sqrt{2}}\ =\ \frac{-1}{\sqrt{2}}$
Q. 3.20 For any arbitrary motion in space, which of the following relations are true :
(a) $v_{average}=\left ( 1/2 \right )\left [ v\left ( t_{1} \right )+v\left ( t_{2} \right ) \right ]$
(b) $v_{average}=\left [ r\left ( t_{2} \right ) -r\left ( t_{1} \right )\right ]/\left ( t_{2}-t_{1} \right )$
(c) $v(t)=v\left ( 0 \right )+a\; t$
(d) $v(t)=r\left ( 0 \right )+v\left ( 0 \right )t+\left ( 1/2 \right )a\; t^{2}$
(e) $a_{average}=\left [ v(t_{2})-v(t_{1}) \right ]/\left ( t_{2}-t_{1} \right )$
Answer:
(a) False:- Since it is an arbitrary motion so the following relation cannot hold for all the arbitrary relations.
(b) True:- This is true as this relation relates displacement with time correctly.
(c) False: - The given equation is valid only in the case of uniform acceleration motion.
(d) False:- The given equation is valid only in the case of uniform acceleration motion. But this is an arbitrary motion, so acceleration can be non-uniform.
(e) True:- This is the universal relation between acceleration and velocity-time, as the definition of acceleration is given by this.
Q. 3.21 Read each statement below carefully and state, with reasons and examples, if it is true or false :
A scalar quantity is one that
(a) is conserved in a process
(b) can never take negative values
(c) must be dimensionless
(d) does not vary from one point to another in space (e) has the same value for observers with different orientations of axe
Answer:
(a) False: For e.g. energy is a scalar quantity but is not conserved in inelastic collisions.
(b) False:- For example, temperature can take negative values in degrees Celsius.
(c) False:- Since speed is a scalar quantity, but has dimensions.
(d) False:- Gravitational potential varies in space from point to point.
(e) True:- Since it doesn't have a direction.
Answer:
The given situation is shown in the figure:-
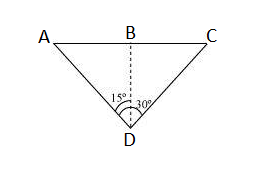
To find the speed of the aircraft, we just need to find the distance AC, as we are given t = 10 sec.
Consider $\Delta$ ABD,
$\tan 15^{\circ}\ =\ \frac{AB}{BD}$
$AB\ =\ \ BD\ \times \tan 15^{\circ}$
or $AC\ =\ 2AB\ =\ \ 2BD\ \times \tan 15^{\circ}$
or $=\ \ 2\times 3400\times \tan 15^{\circ}$
or $=\ 1822.4\ m$
Thus, the speed of aircraft :
$=\ \frac{1822.4}{10}\ =\ 182.24\ m/s$
Motion in a Plane NCERT Solutions: Additional Questions
Motion in a Plane NCERT Solutions: Additional Questions provide extra practice beyond the textbook, covering concepts like vectors, projectile motion, and uniform circular motion. These questions help students build a deeper understanding, improve accuracy, and prepare effectively for exams and competitive tests.
Answer:
The given situation is shown in the figure:-
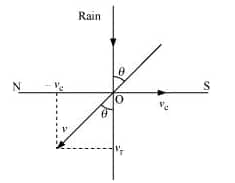
Since both rain and the woman are having some velocity so we need to find the relative velocity of rain with respect to the woman.
$V\ =\ V_{rain}\ +\ (-V_{woman})$
$=\ 30\ +\ (-10)$
$=\ 20\ m/s$
And the angle is given by :
$\tan\Theta \ =\ \frac{V_{woman}}{V_{rain}}$
$\tan\Theta \ =\ \frac{10}{30}$
$\Theta \ \approx \ 18^{\circ}$
Hence woman needs to hold an umbrella at 18 degrees from vertical towards the south.
Answer:
The speed of man is (swim speed ) = 4 Km/h.
Time taken to cross the river will be :
$=\ \frac{Distance}{Speed}$
$=\ \frac{1}{4}\ =\ 15\ min.$
Total distance covered due to the flow of the river:-
$=\ Speed\ of\ river \times Time\ taken$
$=\ 3\times\frac{1}{4}\ =\ 0.75\ Km$
Answer:
According to the question, the figure is shown below:-
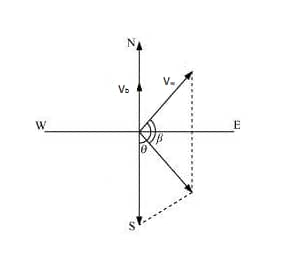
The angle between the velocity of the wind and the opposite of the velocity of the boat is (90 + 45) = 135 degrees.
Using geometry,
$\tan \beta \ =\ \frac{51\sin (90+45)}{72\ +\ 51 \cos (90+45) }$
$\tan \beta \ =\ \frac{51}{50.8 }$
Thus $\beta \ =\ \tan^{-1} \frac{51}{50.8 }=\ 45.11^{\circ}$
So the flag will be just 0.11 degrees from the perfect east direction.
Answer:
No, a vector doesn't have a definite location, as a vector can be shifted in a plane by maintaining its magnitude and direction.
A vector can change with time, for e.g. displacement vector.
No, two equal vectors at different locations may not have identical physical effects. For e.g., two equal force vectors at a different location may have different torques, but when they are applied together, the net torque would be different.
Answer:
The main condition for a physical quantity to be a vector is that it should obey the law of vector addition. Also, the vector has both direction and magnitude, but these are not sufficient conditions. For e.g. current has both magnitude and direction but is a scalar quantity as it doesn't follow the law of vector addition.
Rotation is not a vector on a large basis, as it is measured by an angle which follows the law of scalar addition.
Q.6(a) Can you associate vectors with (a) the length of a wire bent into a loop? Explain.
Answer:
No, the length of a wire bent into a loop cannot be expressed in vector form, as we have no direction associated with it.
Q.6(b) Can you associate vectors with (b) a plane area? Explain.
Answer:
The plane area can be expressed in vector form, and the direction can be associated as pointing outward or inward (normal to the plane) of the area.
Q. 6(c) Can you associate vectors with (c) a sphere? Explain.
Answer:
No, a vector cannot be associated with a sphere, as direction cannot be associated with a sphere anyhow.
Answer:
The range of the bullet is given to be: R = 3 Km.
$R\ =\ \frac{u^2\ \sin 2\Theta }{g}$
or $3\ =\ \frac{u^2\ \sin 60^{\circ} }{g}$
or $\frac{u^2}{g}\ =\ 2\sqrt{3}$
Now, we will find the maximum range (maximum range occurs when the angle of projection is 45 0 ).
$R_{max}\ =\ \frac{u^2\ \sin 2(45^{\circ}) }{g}$
or $R_{max}=\ 3.46\ Km$
Thus, the bullet cannot travel up to 5 Km.
Answer:
According to the question, the situation is shown below:-
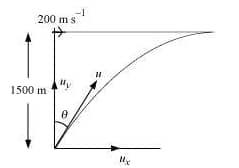
Now, the horizontal distance travelled by the shell = Distance travelled by the plane
or $u \sin \Theta \ t\ =\ vt$
or $\sin \Theta \ =\ \frac{v}{u}$
or $\sin \Theta=\ \frac{200}{600}$
So, $\Theta \ =\ 19.5^{\circ}$
So, the required height will be:-
$H\ =\ \frac{u^2\ \sin^2(90\ -\ \Theta )}{2g}$
or $H=\ \frac{600^2\ \cos^2 \Theta }{2g}$
or $H=\ 16006.48\ m$
or $H=\ 16\ Km$
Answer:
Speed of cycle = 27 Km/h = 7.5 m/s
The centripetal acceleration is given by :
$a_c\ =\ \frac{v^2}{r}$
$=\ \frac{(7.5)^2}{80}$
$=\ 0.7\ m/s^2$
And the tangential acceleration is given as $0.5\ m/s^2$.
So, the net acceleration becomes :
$a\ =\ \sqrt{a_c^2\ +\ a_T ^2}$
or $=\ \sqrt{(0.7)^2\ +\ (0.5) ^2}$
or $=\ 0.86\ m/s^2$
Now for direction,
$\tan \Theta \ =\ \frac{a_c}{a_T}$
or $\tan \Theta =\ \frac{0.7}{0.5}$
Thus, $\Theta \ =\ 54.46^{\circ}$
where the symbols have their usual meaning.
Answer:
Using the equation of motion in both horizontal and vertical directions.
$v_y\ =\ v_{oy}\ =\ gt$ and $v_x\ =\ v_{ox}$
Now,
$\tan \Theta \ =\ \frac{v_y}{v_x}$
or $\tan \Theta=\ \frac{v_{oy}\ -\ gt}{v_{ox}}$
Thus, $\Theta \ =\ \tan^{-1} \left ( \frac{v_{oy}\ -\ gt }{v_{ox}} \right )$
Q.11 Shows that the projection angle $\theta _{0}$ for a projectile launched from the origin is given by
$\theta _{0}=tan^{-1}\left [ \frac{4h_{m}}{R} \right ]$
where the symbols have their usual meaning.
Answer:
The maximum height is given by :
$h\ =\ \frac{u^2 \sin^2 \Theta }{2g}$
And, the horizontal range is given by :
$R\ =\ \frac{u^2 \sin 2\Theta }{g}$
Dividing both, we get :
$\frac{h}{R}\ =\ \frac{\tan \Theta }{4}$
Hence $\Theta \ =\ \tan^{-1} \left ( \frac{4h }{R} \right )$
Motion in a Plane NCERT Solutions: Higher Order Thinking Skills (HOTS) Questions
Motion in a Plane NCERT Solutions of Higher Order Thinking Skills (HOTS) Questions promote logical and critical thinking when applying concepts such as adding vectors, relative velocity, and projectile motion. Solving these higher-order problems assists the students in the application of the concepts in the real world and the development of the problem-solving abilities of the students who are on their way to appear in competitive examinations such as JEE and NEET.
Q1. A body is projected at t= 0 with a velocity 10ms-1 at an angle of 60o with the horizontal. The radius of curvature of its trajectory at t = 1s is R. Neglecting air resistance and taking acceleration due to gravity g = 10 ms-2, the value of R (in meters) is:
a) 2.8
b)10.3
c)2.5
d)5.1
Answer:

We know that,
$
\begin{aligned}
& a_c=\frac{v^2}{R} \\
& u=10 \mathrm{~m} / \mathrm{s}, \theta=60^{\circ}
\end{aligned}
$
Now, calculating speed at $\mathrm{t}=1 \mathrm{~s}$
$
\begin{aligned}
& v_x=u \cos \theta=10 \times \frac{1}{2}=5 \mathrm{~m} / \mathrm{s} \\
& v_y=u_y-g t \\
& v_y=u \sin \theta-g t=10 \times \frac{\sqrt{3}}{2}-10 \times 1=-1.34 \mathrm{~m} / \mathrm{s}(\text { downward }) \\
& \text { Angle, }(\alpha)=\tan ^{-1}\left(\frac{v_x}{v_y}\right)=\tan ^{-1}\left(\frac{5}{1.34}\right) \\
& a_c=g \sin \alpha \quad \text { (Acceleration perpendicular to speed) } \\
& \Rightarrow g \sin \alpha=\frac{v^2}{R} \\
& \Rightarrow R=\frac{v_x^2+v_y^2}{g \sin \alpha} \\
& R=\frac{25+1.7956}{10 \times 0.9659}=2.8 \mathrm{~m}
\end{aligned}
$
Hence, the answer is option (1).
Q.2. The maximum speed of a boat in still water is $27 \mathrm{~km} / \mathrm{h}$. Now this boat is moving downstream in a river flowing at $9 \mathrm{~km} / \mathrm{h}$. A man in the boat throws a ball vertically upwards with a speed of $10 \mathrm{~m} / \mathrm{s}$. The range of the ball as observed by an observer at rest on the river bank, is _______ cm.
(Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )
a) 2000
b)3000
c)4000
d)5000
Answer:
$\overrightarrow{\mathrm{v}}_{\mathrm{b}}=9+27=36 \mathrm{~km} / \mathrm{hr}$

$
\begin{aligned}
& \overrightarrow{\mathrm{v}}_{\mathrm{b}}=36 \times \frac{1000}{36000}-10 \mathrm{~m} \text { sec } \\
& \text { Time of flight }=\frac{2-10}{10}=2 \mathrm{sec} \\
& \text { Range }=10 \times 2=20 \mathrm{~m}=2000 \mathrm{~cm}
\end{aligned}
$
Hence, the answer is option (1).
Q.3 Two balls are projected with the same velocity but with different angles with the horizontal. Their ranges are equal. If the angle of projection of one is 30° and its maximum height is then the maximum height of the other will be
Answer:
Given: One ball's projection angle is $30^{\circ}$
Explanation:
The question tells us that the range is equal, so the angles of projection must be complementary for the range to be equal.
Now, let us consider the angle of projection of one ball is $\theta_1$, and another ball is $\theta_2$
$
\begin{aligned}
& \theta_1=30^0 \\
& \therefore \theta_2=90^0-30^0=60^{\circ}
\end{aligned}
$
By using known values in the formula, we can now determine the maximum range of each ball.
$
h_1=\frac{\mu^2 \sin ^2\left(\theta_1\right)}{2 g}=\frac{\mu^2}{8 g}=h
$
Now, for the second ball
$
h_2=\frac{\mu^2 \sin ^2\left(\theta_2\right)}{2 g}=\frac{3 \mu^2}{8 g}=3 h
$
Hence, the maximum height of others will be 3 h
Hence, the answer is 3h.
Q 4. A swimmer crosses the river along the line, making an angle of 45º with the direction of flow. The velocity of the river is 5 m/s. A swimmer takes 6 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be:
Answer:
River flow along the y direction with a velocity of 5 $\hat{j}$ m/s.
The swimmer crossover along the vector $\hat{i} + \hat{j}$ since the angle is 45 degree
displacement of swimmer just after crossing = 60 $\hat{i} + 60 \hat{j}$ meters
speed of the swimmer with respect to a stationary observer
= (60 $\hat{i}$ + 60 $\hat{j}$) 6 m/s = 10 $\hat{i}$ + 10 $\hat{j}$ m/s
velocity of swimmer relative to the river = 10 $\hat{i}$ + 10 $\hat{j}$ - 5 $\hat{j}$
magnitude of velocity relative to river = 5√5 m/s
Hence, the answer is 5√5.
Q 5. A man wearing a hat of extended length 12 cm is running in rain falling vertically downwards with a speed of 10 m/s. The maximum speed with which a man can run, so that raindrops do not fall on his face (the length of his face below the extended part of the hat is 16 cm) will be : (please give your answer in m/s)
Answer:
for Rain - Man Problem -
$
\tan \Theta=\frac{V_m}{V_r}
$
$\Theta=$ angle, which relative velocity of rain with
respect to man makes with the vertical
- wherein
$\vec{V}_r=$ velocity of rain falling vertically
$\overrightarrow{V_m}=$ velocity of man in the horizontal direction
$
V_{R / G(x)}=0, V_{R / G(y)}=10 \mathrm{~m} / \mathrm{s}
$
Let the velocity of $m a n=V$
$
\tan \theta=\frac{16}{12}=\frac{4}{3}
$
then, $\quad V_{R / \operatorname{man}}=V$ (opposite to man)
For the required conditions:
$
\begin{aligned}
& \tan \theta = \frac{V_{R / M(y)}}{V_{R / M(x)}}=\frac{10}{V}=\frac{4}{3} \\
& \Rightarrow V=\frac{10 \times 3}{4}=7.5
\end{aligned}
$
Hence, the answer is 7.5.
Class 11 Physics Chapter 3 - Motion in a Plane: Topics
Class 11 Physics Chapter 3 - Motion in a Plane is a step higher than motion in a straight line because it introduces students to the study of motion in two dimensions. The chapter discusses some fundamental concepts, such as vectors, projectile motion, uniform circular motion, and the addition of vectors, which are the foundation of advanced physics. Knowledge of such topics can be used not only in the CBSE exams but also in competitive exams such as JEE and NEET.
3.1 Introduction
3.2 Scalars And Vectors
3.2.1 Position And Displacement Vectors
3.2.2 Equality Of Vectors
3.3 Multiplication Of Vectors By Real Numbers
3.4 Addition And Subtraction Of Vectors — Graphical Method
3.5 Resolution Of Vectors
3.6 Vector Addition – Analytical Method
3.7 Motion In A Plane
3.7.1 Position Vector And Displacement
3.8 Motion In A Plane With Constant Acceleration
3.9 Projectile Motion
3.10 Uniform Circular Motion
NCERT Solutions for Class 11 Physics Chapter 3 - Motion in a Plane: Important Formulae
The useful formulae in this chapter are useful in the solution of numerical problems on velocity, acceleration and displacement and time in different directions. These are the significant formulas to learn complex motion, and you need them in board exams as well as in competitive tests such as JEE and NEET.
Vector Representation
- Vector $\vec{A}$ in component form:
$
\vec{A}=A_x \hat{i}+A_y \hat{j}
$
Where:
$
A_x=A \cos \theta, \quad A_y=A \sin \theta
$
- Magnitude of vector:
$
|\vec{A}|=\sqrt{A_x^2+A_y^2}
$
- Direction (angle with $x$-axis):
$
\theta=\tan ^{-1}\left(\frac{A_y}{A_x}\right)
$
Vector Addition
- If $\vec{R}=\vec{A}+\vec{B}$, then:
$\begin{aligned} \vec{R} & =\left(A_x+B_x\right) \hat{i}+\left(A_y+B_y\right) \hat{j} \\ |\vec{R}| & =\sqrt{\left(A_x+B_x\right)^2+\left(A_y+B_y\right)^2}\end{aligned}$
Projectile Motion
- Horizontal Range
$
R=\frac{u^2 \sin (2 \theta)}{g}
$
- Time of Flight
$
T=\frac{2 u \sin \theta}{g}
$
- Maximum Height
$
H=\frac{u^2 \sin ^2 \theta}{2 g}
$
- Equation of Trajectory:
$
y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta}
$
Approach to Solve Questions of Class 11 Physics Chapter 3 - Motion in a Plane
When an object travels inside two dimensions, its route becomes more appealing and complicated than a straightforward straight-line motion. Chapter 3 - Motion in a Plane exposes students to some of the interesting topics of vectors, projectiles, and circular motion that we encounter in our daily lives, such as a ball in flight or a car at a curved turn. In order to be able to find the answers to the questions in this chapter, students need to study both the formulas and the reasoning behind the representation of vectors and the systematic approach of solving numerical problems.
- Begin by revising the fundamental concepts of vectors, such as magnitude and direction, as a majority of the questions in this chapter deal with the quantities of vectors, such as displacement, velocity and acceleration.
- Understand how to express and solve vectors in terms of components along the x and y axes because this step is essential in solving two-dimensional problems of motion.
- Practice with the laws of addition and subtraction of vectors, since most numerical problems require the determination of the resultant values through the application of these laws.
- Study problems of projectile motion and learn to distinguish between horizontal and vertical motion, and solve them separately using kinematic equations.
- Memorise the derivations of key formulas such as time of flight, range and maximum height because they tend to be used both conceptually and numerically.
- Visualise change of direction and magnitude by using vector diagrams, particularly in relative velocity and circular motion questions.
- Solve past year questions, NCERT exemplar problems, to become familiar with the various types of questions, like graphical analysis, and angle-based problems of motion.
- Lastly, memorise important equations and units to be sure of their accuracy and to eliminate errors in exams.
How Can NCERT Solutions for Class 11 Physics Chapter 3 Motion in a Plane Help in Exam Preparation?
The class 11 physics chapter 3 Motion in a Plane question answers serve as an excellent reference material in the understanding of the idea of motion in two dimensions, including displacement, velocity, acceleration and the projectile motion. Such Motion in a Plane class 11 question answers make it easier to use vector algebra and assist students in relating the theoretical concepts with numerical ones. Through the NCERT questions, the students gain a good base for solving graph-based and derivation-based questions that most exams have. The step-by-step Motion in a Plane class 11 question answers are clear and generate confidence in the solving of complex multi-directional motion problems and guarantee conceptual clarity. A frequent revision with such class 11 physics Motion in a Plane question answers can make students stronger in their critical thinking and able to score higher in CBSE board exams and entrance tests such as JEE and NEET.
What Extra Should Students Study Beyond NCERT for JEE?
To prepare for JEE, one cannot study the NCERT alone to cover Motion in a Plane. The chapter requires more abstraction, higher-order problem-solving capabilities and more diverse applications. Students are expected to learn about vectors, projectile motion, and relative velocity in two dimensions, with advanced motion not taught under NCERT.
Also, Check NCERT Books and NCERT Syllabus here
NCERT Solutions for Class 11 Physics Chapter Wise
Subject-wise NCERT solutions
- NCERT solutions for class 11 Mathematics
- NCERT solutions for class 11 Chemistry
- NCERT solutions for class 11 Physics
- NCERT solutions for class 11 Biology
Subject-wise NCERT Exemplar solutions
Frequently Asked Questions (FAQs)
Yes, these NCERT Solutions for Class 11 Physics Chapter 3 are full of detail. They offer extensive, step-by-step solutions to all in-text questions, as well as exercises present at the end of each chapter. For your convenience, the solutions are also offered as a free PDF and have been completely updated for the 2025–2026 academic year.
Uniform circular motion is tested in JEE, NEET examinations along with projectile motion and relative velocity.
When it comes to projectile motion problems, the most common mistake is breaking down the starting velocity into its constituent parts (v cos θ and v sin θ). Our solutions avoid this by openly displaying the resolution of vectors as the first step and always beginning with a clear diagram. This creates the proper basis for precisely figuring out the range, maximum height, and time of flight.
Its uses are in sports (such as hitting a cricket ball), aviation, navigation and satellite movement.
It can allow us to comprehend the real-world movements which take place in two realms, such as the movement of a ball or a satellite.
Resolve the motion into a horizontal and vertical part and apply kinematic equations to each.
Yes, most of the problems require basic knowledge of vector algebra.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
