Revise by reading short notes and formula sheets regularly, practising NCERT intext and exercise questions, and solving numericals on Kc, Kp, pH, buffers, and solubility product. Use flowcharts and diagrams to visualise concepts, and review past year questions for quick and effective exam preparation.
NCERT Class 11 Chemistry Chapter 7 Notes Equilibrium - Download PDF
What if a chemical reaction didn’t go all the way but instead decided to settle halfway? That’s exactly what happens in equilibrium! In this chapter, you'll explore the science behind reversible reactions, where the forward and backwards processes occur simultaneously. Equilibrium is one of the most crucial concepts in chemistry, as it explains how chemical and physical processes reach a state of balance. Have you ever wondered why the chemical reactions in a closed container stop changing after a while? Such phenomena are very well explained by concepts provided in the equilibrium discipline of physical chemistry.
This Story also Contains
- NCERT Notes for Class 11 Chemistry Chapter 6 Equilibrium: Download PDF
- NCERT Notes for Class 11 Chemistry Chapter 6 Equilibrium
- Equilibrium Previous Years Questions and Answers
- How to Master Class 11 Chemistry Chapter 6 Equilibrium
- NCERT Class 11 Notes Chapter-Wise
- NCERT Solutions for Class 11 Chemistry
- Subject-Wise NCERT Exemplar Solutions
- Subject-Wise NCERT Solutions
Chemical equilibrium refers to a state in which neither the reactants nor the products can alter any further. In this situation, the forward and backward reaction rates stay constant. For students to grasp advanced concepts, the concept of equilibrium becomes crucial. NCERT Notes for Class 11 are structured according to the latest NCERT syllabus, and from the exam perspective, as many questions are asked from Chemical Equilibrium in JEE Mains and NEET examinations. By referring to class 11 chemistry chapter 6 equilibrium notes , students can gain a deeper understanding of equilibrium reactions, Le Chatelier's Principles On Equilibrium, and factors affecting equilibrium. Along with this, the NCERT notes of other chapters are also prepared by our subject matter experts, which can help students in their preparation.
NCERT Notes for Class 11 Chemistry Chapter 6 Equilibrium: Download PDF
Download the ncert class 11 chemistry chapter 6 equilibrium notes pdf to access a clear explanation, important reactions of this chapter. These NCERT Notes for Class 11 Chemistry cover all the key concepts of the Equilibrium. You can download the PDF from the button given below.
Also Read
NCERT Notes for Class 11 Chemistry Chapter 6 Equilibrium
The chapter Equilibrium explores the balance that exists in physical and chemical processes. It helps us understand how reactions reach a stable state, how equilibrium is maintained, and how factors like temperature, pressure, and concentration affect it. NCERT Class 11 Chemistry Chapter 6 Notes Equilibrium also introduces key concepts like the equilibrium constant, Le Chatelier’s Principle, and the ionic product of water, forming the foundation for understanding acid-base reactions, buffer solutions, and solubility equilibria in chemistry. To get a clearer understanding of these concepts, you can refer to NCERT Solutions.
Equilibrium in Physical Processes
Equilibrium is a state in which the forces on both sides are equal. It is a moment in a chemical reaction where the rate of forward reaction equals the rate of backward reaction, according to chemistry. Or, to look at it another way, it is the state in which the concentrations of reactants and products are equal.
All physical processes attain this when all state variables, such as pressure, temperature, and so on become constant. There are three types of this.
1. Solid-liquid equilibrium
Ice and water are in equilibrium at a specific temperature and pressure. The temperature at which the solid and liquid phases of any pure substance are in equilibrium at atmospheric pressure is known as the normal melting point or normal freezing point of the substance. When the system is in dynamic equilibrium, the following conditions will be implemented,
Both opposing processes occur at the same time.
Because both processes happen at the same time, the volume of ice and water stays the same.
2. Liquid-vapour equilibrium
This reaction shows the conversion of water to vapour. The number of water molecules that pass from the gaseous to the liquid state increases until equilibrium is established.
rate of evaporation $=$ rate of condensation
The constant temperature at which the vapour pressure of a liquid equals atmospheric pressure is known as the boiling point. Temperature is the state variable that becomes constant.
3. Solid-vapour equilibrium
$\mathrm{I}_2$ (solid) $\Leftrightarrow \mathrm{I}_2$ (vapour)
Camphor(solid) $\Leftrightarrow$ Camphor(vapour)
$\mathrm{NH}_4 \mathrm{Cl}$ (solid) $\Leftrightarrow \mathrm{NH}_4 \mathrm{Cl}$ (vapour)
At equilibrium Rate of solidification $=$ the Rate of evaporation
4. Equilibrium involving the dissolution of solids or liquids in gases
Dissolution occurs when a solid dissolves in a liquid. The forward reaction is dissolution in this case. When the solvent is unable to dissolve any more solute, crystallization occurs in a reverse reaction. At equilibrium, the rate of dissolution equals the rate of crystallization. Concentration is the state variable that remains constant. Students can also download equilibrium class 11 chemistry chapter 6 CBSE notes for quick revision and better exam preparation.
General characteristics of physical equilibrium
- The properties that can be measured become constant.
- It can only be accomplished in a closed vessel.
- The opposing forces become equal at equilibrium.
- The concentration is constant at equilibrium.
- The magnitude of the equilibrium value indicates the reaction's extent.
- The equilibrium is dynamic. That is, the reaction continues, but the rate remains constant.
- Equilibrium in a chemical process
Chemical reactions, like physical systems, reach a point of equilibrium. Those chemical processes can take place both forward and backwards. When the rate of forward reaction equals the rate of backwards reaction, the chemical equilibrium is dynamic.
Some features of physical equilibria are given in the table below.
| Process | Conclusion |
|---|---|
| Liquid $\rightleftharpoons$ Vapour $\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(\mathrm{g})$ | $P_{\mathrm{H}_2 \mathrm{O}}$ is constant at a given temperature |
| Solid $\rightleftharpoons$ Liquid $\mathrm{H}_2 \mathrm{O}(\mathrm{s}) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(\mathrm{l})$ | The melting point is fixed at constant pressure |
| Solute $(s) \rightleftharpoons$ Solute $($ solution $)$ Sugar $(s) \rightleftharpoons$ Sugar (solution) | The concentration of solute in solution is constant at a given temperature |
| $\mathrm{Gas}(\mathrm{g}) \rightleftharpoons \mathrm{Gas}(\mathrm{aq}) \mathrm{CO}_2(\mathrm{~g}) \rightleftharpoons \mathrm{CO}_2(\mathrm{aq})$ | [gas(aq)]/[gas(g)] is constant at a given temperature $\left[\mathrm{CO}_2(\mathrm{aq})\right] /\left[\mathrm{CO}_2(\mathrm{~g})\right]$ is constant at a given temperature |
EQUILIBRIUM IN CHEMICAL PROCESSES – DYNAMIC EQUILIBRIUM
Chemical reactions can be reversible, proceeding in both forward and backwards directions. When the rates of forward and reverse reactions become equal, the concentrations of reactants and products remain constant—this is the state of dynamic equilibrium. For a general reaction,
$
A+B \rightleftharpoons C+D
$
With passage of time, there is accumulation of the products C and D and depletion of the reactants A and B, as shown in the figure below.
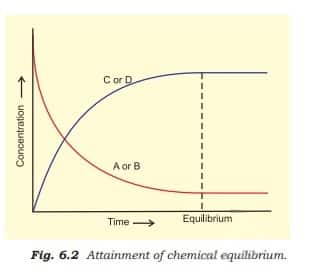
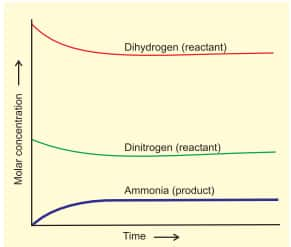
This dynamic nature was demonstrated in Haber's process for ammonia synthesis:
$
\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightleftharpoons 2 \mathrm{NH}_3(g)
$
For $\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{~g})$, If we start with equal initial concentration of H2 and I2, the reaction proceeds in the forward direction and the concentration of H2 and I2 decreases while that of HI increases, until all of these become constant at equilibrium.
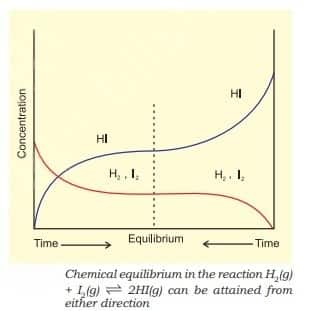
Reversible reactions
With the passage of time, the concentrations of reactants A and B decline while the concentrations of products C and $D$ increase, resulting in a decrease in forward reaction and an increase in backward reaction rates. The system will attain equilibrium when the two reactions occur at the same pace.
Irreversible reactions
The irreversible reaction occurs when the products generated do not react again to form reactants under the same conditions. It is impossible for these reactions to occur in the opposite direction.
Characteristics of chemical equilibrium
- At equilibrium, the concentrations of each of the reactants and products become constant.
- At equilibrium, the rate of the forward reaction equals the rate of the backward reaction, implying that equilibrium is dynamic.
- Only chemical equilibrium can be achieved if none of the products are permitted to escape or separate as a solid.
LAW OF CHEMICAL EQUILIBRIUM AND EQUILIBRIUM CONSTANT
At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentrations of the reactants raised to their individual stoichiometric coefficients has a constant value. This is known as the Equilibrium Law or Law of Chemical Equilibrium.
On the basis of experimental studies of many reversible reactions, the Norwegian chemists Cato Maximillian Guldberg and Peter Waage proposed in 1864 that the concentrations in an equilibrium mixture are related by the following equilibrium equation,
$
K_c=\frac{[\mathrm{C}][\mathrm{D}]}{[\mathrm{A}][\mathrm{B}]}
$
where $K_c$ is the equilibrium constant and the expression on the right side is called the equilibrium constant expression.
Equilibrium Constant
A reactant and product mixture in equilibrium is referred to as an equilibrium mixture.
The product of reaction product concentrations raised to their separate stoichiometric coefficients in the balanced chemical equation, divided by the product of reactant concentrations raised to their individual stoichiometric coefficients, has a constant value at a given temperature. This is the Equilibrium Law, sometimes known as the Law of Chemical Equilibrium.
The ratio of the concentration of products to the concentration of reactants is defined as the equilibrium constant of a chemical reaction at equilibrium.
The equilibrium constant for a general reaction,
$
a A+b B \rightleftharpoons c C+d D
$
is expressed as,
$
K_c=[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{\mathrm{d}} /[\mathrm{A}]^{\mathrm{a}}[\mathrm{~B}]^{\mathrm{b}}
$
where $[A],[B],[C]$ and $[D]$ are the equilibrium concentrations of the reactants and products.
Equilibrium constant for the reaction, $4 \mathrm{NH}_3(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{g})$ is written as
$
K_c=[\mathrm{NO}]^4\left[\mathrm{H}_2 \mathrm{O}\right]^6 /\left[\mathrm{NH}_3\right]^4\left[\mathrm{O}_2\right]^5
$
Characteristics
- The value of the equilibrium constant for a given reaction is always constant, regardless of the concentrations of the reactants with which we begin or the direction from which the equilibrium was approached.
- If " K " is the equilibrium constant, then the equilibrium constant of the reversed reaction is given by $1 / \mathrm{K}$.
- Let K is the equilibrium constant.If the equation is divided by 2 the equilibrium constant will changed to K .
- Let K be the equilibrium constant. If the equation is multiplied by 2 , the equilibrium constant will change to K 2
- The value of the equilibrium will not be affected by adding a catalyst to the reaction.
Applications of the equilibrium constant
1. Predicting the extent of reaction
- The equilibrium constant is related to the extent of the reaction
- The reaction moves forward if the value of k is large.
- If the value of k is less than one, the reaction is in the backward direction.
- If k> $10^3$, the extent is considerable in this case, and the reaction is practically complete.
- If k is less than $10^{-3}$, the reaction will proceed to a lesser extent.
- If k is less than $10^{-3}$, the reaction will proceed to a lesser extent.
- There is a significant concentration of reactants and products if the value of $k$ is between $10^{-3}$ and $10^3$
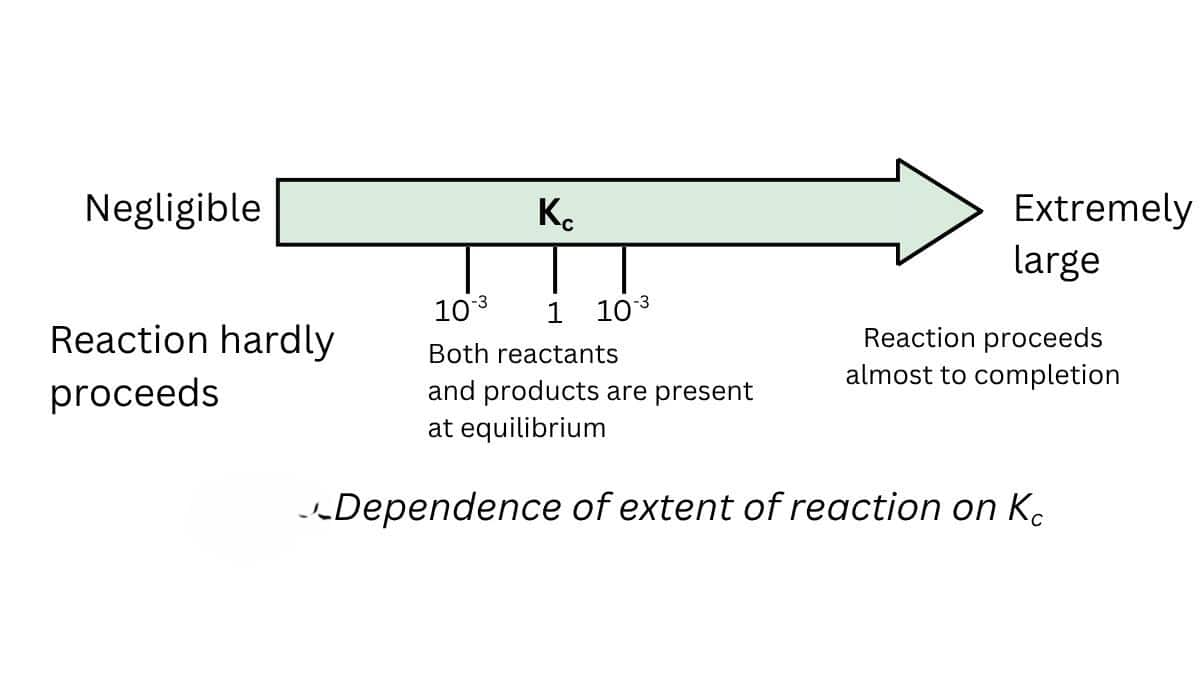
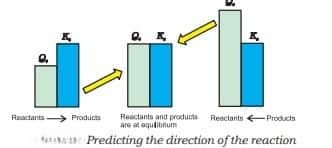
2. Predicting the direction of the reaction
- It indicates whether the reaction is going in the direction of the product or reactant. $Q$ is the reaction quotient.
- Reactants predominate if $\mathrm{Q}<\mathrm{k}$.
- Reaction is at equilibrium if $\mathrm{Q}=\mathrm{k}$.
- Products predominate if $\mathrm{Q}>\mathrm{k}$.
3. Calculating Equilibrium Concentrations
-
Write the balanced chemical equation.
-
Set up an ICE table (Initial, Change, Equilibrium) using:
-
Initial concentrations
-
Changes in terms of x
-
Equilibrium expressions
-
-
Substitute equilibrium concentrations into the equilibrium expression and solve for x.
-
Calculate equilibrium concentrations using the value of x.
-
Verify by substituting back into the equilibrium expression.
Homogeneous and Heterogeneous Equilibria
Homogeneous equilibrium
A homogenous system is an equilibrium system in which all of the reactants and products are in the same phase. For example, in the gaseous reaction, $\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) 2 \mathrm{NH}_3(\mathrm{~g})$, reactants and products are in the homogeneous phase.
Equilibrium Constant in Gaseous Systems
For reaction involving concetration, we calculate the equilibrium in terms of Kc , and for reactions involving gases, it is usually more convenient to express the equilibrium constant in terms of partial pressure.
For a general reaction
$
\begin{aligned}
\mathrm{a} \mathrm{~A} & +\mathrm{b} \mathrm{~B} \rightleftharpoons \mathrm{c} \mathrm{C}+\mathrm{d} \mathrm{D} \\
K_p & =\frac{\left(p_c^c\right)\left(p_D^d\right)}{\left(p_A^a\right)\left(p_B^b\right)}=\frac{[\mathrm{C}]^c[\mathrm{D}]^d(\mathrm{RT})^{(c+d)}}{[\mathrm{A}]^a[\mathrm{~B}]^b(\mathrm{RT})^{(a+b)}} \\
& =\frac{[\mathrm{C}]^c[\mathrm{D}]^d}{[\mathrm{~A}]^a[\mathrm{~B}]^b}(\mathrm{RT})^{(c+d)-(a+b)} \\
& =\frac{[\mathrm{C}]^c[\mathrm{D}]^d}{[\mathrm{~A}]^a[\mathrm{~B}]^b}(\mathrm{RT})^{\Delta n}=K_c(\mathrm{RT})^{\Delta n}
\end{aligned}
$
where $\Delta n=$ (number of moles of gaseous products) - (number of moles of gaseous reactants) in the balanced chemical equation.
Heterogeneous equilibrium
Heterogeneous equilibrium refers to an equilibrium system with many phases. The equilibrium between water vapour and liquid water in a closed container is a well-known example of this type of system.
The equilibrium between water vapour and liquid water in a closed container is an example of heterogeneous equilibrium.
$
\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(\mathrm{~g})
$
In this example, there is a gas phase and a liquid phase. In the same way, equilibrium between a solid and its saturated solution,
$
\mathrm{Ca}(\mathrm{OH})_2(\mathrm{~s})+(\mathrm{aq}) \rightleftharpoons \mathrm{Ca}^{2+}(\mathrm{aq})+2 \mathrm{OH}^{-}(\mathrm{aq})
$
is a heterogeneous equilibrium.
Equilibrium Constant in the Gaseous State
Partial pressures are useful for gaseous processes because partial pressure is directly proportional to concentration at any fixed temperature. In the case of a typical gaseous reaction
$a A+b B \Leftrightarrow c C+d D$
$K p=p C^C \cdot p D^d / p A^a \cdot p B^b$
Relationship between Kc and Kp
$P V=n R T$
P=nRT/V
$\mathrm{P}=\mathrm{CRT}$
For the reaction
$\mathrm{H}_2+\mathrm{I}_2 \Leftrightarrow 2 \mathrm{HI}$
$
\begin{aligned}
& K_{\mathrm{c}}=\frac{[\mathrm{HI}(\mathrm{~g})]^2}{\left[\mathrm{H}_2(\mathrm{~g})\right]\left[\mathrm{I}_2(\mathrm{~g})\right]} \\
& \text { or } K_c=\frac{\left(p_{\mathrm{H}}\right)^2}{\left(p_{\mathrm{H}_2}\right)\left(p_{\mathrm{I}_2}\right)}
\end{aligned}
$
Further, since $p_{\mathrm{HI}}=[\mathrm{HI}(\mathrm{g})] \mathrm{R} T$
$
\begin{aligned}
p_{\mathrm{I}_2} & =\left[\mathrm{I}_2(\mathrm{~g})\right] \mathrm{R} T \\
p_{\mathrm{H}_2} & =\left[\mathrm{H}_2(\mathrm{~g})\right] \mathrm{R} T
\end{aligned}
$
Therefore,
$
\begin{aligned}
K_p= & \frac{\left(p_{\mathrm{HI}}\right)^2}{\left(p_{\mathrm{H}_2}\right)\left(p_{\mathrm{I}_2}\right)}=\frac{[\mathrm{HI}(\mathrm{~g})]^2[\mathrm{RT}]^2}{\left[\mathrm{H}_2(\mathrm{~g})\right] \mathrm{RT} \cdot\left[\mathrm{I}_2(\mathrm{~g})\right] \mathrm{RT}} \\
& =\frac{[\mathrm{HI}(\mathrm{~g})]^2}{\left[\mathrm{H}_2(\mathrm{~g})\right]\left[\mathrm{I}_2(\mathrm{~g})\right]}=K_c
\end{aligned}
$
In this example, Kp = Kc i.e., both equilibrium constants are equal.
Relationship Between Equilibrium Constant and Gibbs Free Energy
The value of a reaction's equilibrium constant is independent of the rate of reaction. But it is directly related to the Gibbs free energy as below,
- If the change in Gibbs free energy, $\Delta \mathrm{G}$ is negative, the reaction proceeds spontaneously in the forward direction.
- If the change in Gibbs free energy, $\Delta G$ is positive, the forward reaction products must be transformed to reactants through a non-spontaneous mechanism.
- If the change in Gibbs free energy is zero, the reaction is in equilibrium, and no more free energy is available to drive it.
A mathematical expression of this thermodynamic view of equilibrium can be described by the following equation:
$
\Delta G=\Delta G^{\ominus}+\mathrm{RT} \ln Q
$
where, $G^{\ominus}$ is standard Gibbs energy.
At equilibrium, when $\Delta G=0$ and $Q=K_c$, the equation (6.21) becomes,
$
\begin{aligned}
& \Delta G=\Delta G^{\ominus}+\mathrm{R} T \ln K=0 \\
& \Delta G^{\ominus}=-\mathrm{R} T \ln K \\
& \ln K=-\Delta G^{\ominus} / \mathrm{R} T
\end{aligned}
$
Factors Affecting Equilibria
Le Chatelier's principle
This principle helps in examining the reaction's progress and making a qualitative prediction about how changes in conditions will affect equilibrium. It states that "If an equilibrium is subjected to a change of concentration, pressure or temperature, the equilibrium shifts in the direction that trends to undo the effect of the change". This principle is applicable to all physical and chemical systems .
Effect of concentration change
The addition or removal of any reactant or product, in general, disturbs the equilibrium. According to Le Chatelier's principle, the direction of the net reaction that consumes the added substance reduces the concentration of the added reactant or product. "When the concentration of any of the reactants or products in an equilibrium reaction is changed, the equilibrium mixture's composition changes to minimize the influence of concentration variations."
When $\mathrm{H}_2$ is added to the equilibrium mixture of
$
\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g})=2 \mathrm{HI}(\mathrm{~g})
$
the equilibrium shifts right to consume added $\mathrm{H}_2$ and form more HI.
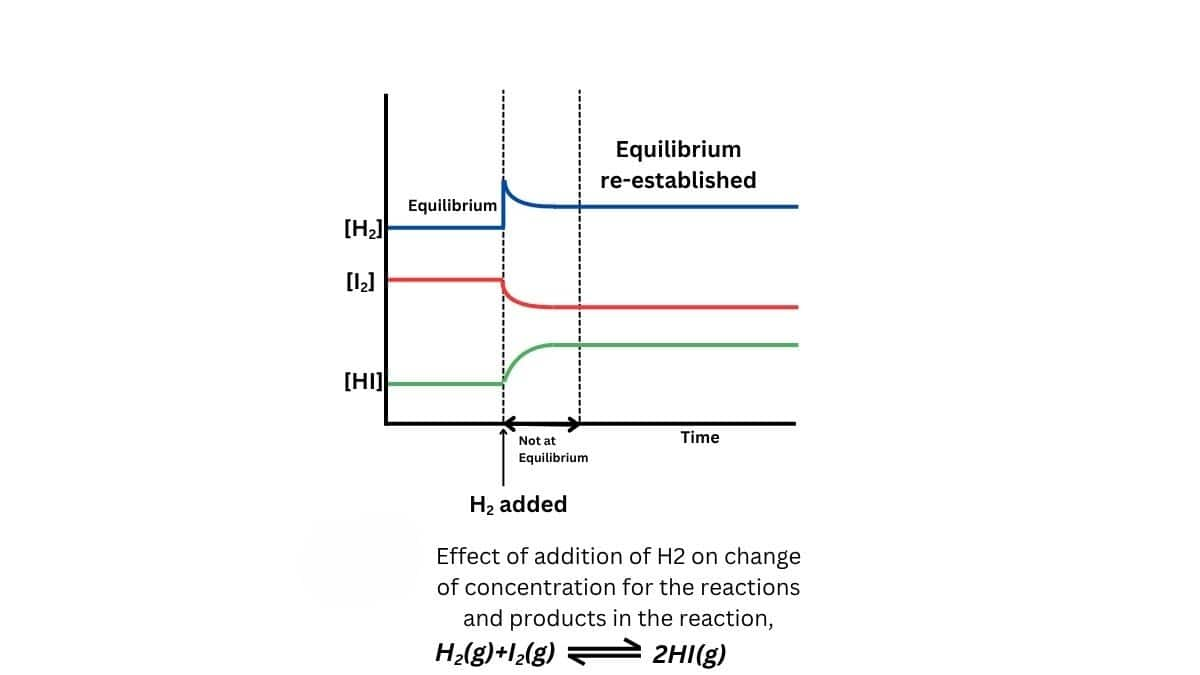
This follows Le Chatelier's principle, which states that adding a reactant shifts the equilibrium to reduce its concentration, establishing a new balance.
The same point can be explained in terms of the reaction quotient, $Q_c$,
$
Q_c=[\mathrm{HI}]^2 /\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]
$
Effect of temperature change
If there is a change in temperature there is a change in equilibrium constant. The sign of the $\Delta \mathrm{H}$ for the reaction affects the temperature change dependency of the equilibrium constant. If $\Delta \mathrm{H}$ is negative, the exothermic reaction's equilibrium constant decreases as the temperature rises. If $\Delta \mathrm{H}$ is positive, the endothermic reaction's equilibrium constant increases as the temperature falls.
Effect of temperature can be seen in an endothermic reaction,
$
\begin{gathered}
{\left[\mathrm{Co}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{3+}(\mathrm{aq})+4 \mathrm{Cl}^{-}(\mathrm{aq}) \rightleftharpoons\left[\mathrm{CoCl}_4\right]^{2-}(\mathrm{aq})+} \\
\text { pink } \quad \text { colourless } \quad \text { blue }
\end{gathered}
$
At room temperature, the equilibrium mixture is blue due to $\left[\mathrm{CoCl}_4\right]^{2-}$. When cooled in a freesing mixture, the colour of the mixture turns pink due to $\left[\mathrm{Co}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{3+}$.
Effect of pressure change
A pressure change generated by changing the volume might impact the yield of products in a gaseous reaction when the total number of moles of gaseous products is different. The principle of Le-Chatelier is applied to heterogeneous equilibrium. Change in volume of solids and liquids on the application of pressure is very less so here the effect of pressure change on solids and liquids can be neglected.
Effect of volume change
The effect of a pressure rise is the same as the effect of a volume drop. As a result, the effect of a drop in volume will be moved towards equilibrium in the direction of a decrease in a number of moles.
Effect of Inert Gas Addition
If an inert gas (e.g., argon) is added at constant volume, the equilibrium remains unaffected because it does not change the partial pressures or concentrations of the reactants/products. Only gases involved in the reaction can shift the equilibrium.
Effect of the catalyst
A catalyst is the chemical substance that increases the rate of a chemical reaction by opening up a new low-energy pathway for reactants to become products. The rate of forward and reverse reactions that pass through the transition state is increased by a catalyst, but the equilibrium is not affected.
Ionic Equilibria in Solution
The following is an example of an equilibrium reaction involving ions
Based on their ability to conduct electricity, Michael Faraday divided the substances into two categories, electrolytes and non-electrolytes. The electrolyte solution conducts electricity due to the presence of ions. An aqueous solution of NaCl , for example, is totally dissociated into $\mathrm{Na}^{+}$and $\mathrm{Cl}^{-}$ions due to nearly 100 percent ionization. In the instance of acetic acid, which is a weak electrolyte, ionization occurs to the extent of $5 \%$. In weak electrolytes, equilibrium is thus created between ions and unionized molecules. Ionic Equilibrium is a type of equilibrium involving ions in an aqueous solution.
Strong electrolytes are electrolytes that are quickly broken into ions with complete dissociation. Weak electrolytes are electrolytes that have been partially dissociated into ions.
Acids, Bases, and Salts
The explanation of acids and bases has a variety of theories.
a) Arrhenius concept
According to this theory, acids are substances that generate hydrogen ions when dissolved in water. Eg: HCI
It was later discovered that these hydrogen ions interact with water to create the hydronium ion. Bases are substances that release hydroxide ions when dissolved in water. Eg: NaOH
It was later discovered that just a few compounds do not release hydrogen or the hydroxide ion. However, they continue to behave as acids or bases. As a result, new theories were introduced.
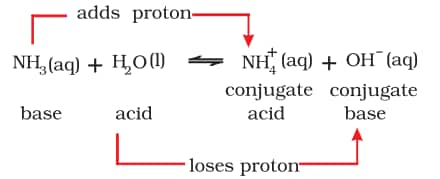
b) Brönsted-Lowry theory
According to the Brönsted-Lowry theory, an acid is a substance that can donate a hydrogen ion, $\mathrm{H}^{+}$, while a base can accept a hydrogen ion, $\mathrm{H}^{+}$. Proton donors are acids, whereas proton acceptors are bases.
Lowry-Bronsted acid and Lowry-Bronsted base are water molecules that act as proton donors and ammonia molecules that act as proton acceptors respectively in this reaction. Consider the example of dissolution of NH3 in H2O represented by the following equation:
c)Lewis concept
According to this concept, an acid is a species that accepts electron pairs, whereas a base is a species that donates them.
Lewis acids: $\mathrm{AlCl}_3, \mathrm{Co}^{3+}, \mathrm{Mg}^{2+}$
Lewis bases: $\mathrm{H}_2 \mathrm{O}, \mathrm{NH}_3, \mathrm{OH}^{-}$
$\mathrm{BF}_3$ does not have a proton but still acts as an acid and reacts with $\mathrm{NH}_3$ by accepting its lone pair of electrons. The reaction can be represented by,
$
\mathrm{BF}_3+: \mathrm{NH}_3 \rightarrow \mathrm{BF}_3: \mathrm{NH}_3
$
Ionization of Acid and Bases
The Arrhenius concept defines acids as substances that produce $\mathrm{H}^{+}\left(\right.$or $\left.\mathrm{H}_3 \mathrm{O}^{+}\right)$ and bases as those that produce OH⁻ in aqueous solutions. Strong acids (e.g., $\mathrm{HCl}, \mathrm{HNO}_3, \mathrm{H}_2 \mathrm{SO}_4$) and bases (e.g., NaOH, KOH, $\mathrm{Ba}(\mathrm{OH})_2$) completely dissociate in water.
The Brønsted-Lowry concept focuses on proton transfer: acids donate protons and bases accept them. In a dissociation equilibrium like
$\mathrm{HA}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{A}^{-}$,
the direction favored depends on the relative strengths of the acids and bases involved. Equilibrium shifts towards the weaker acid and base.
- Strong acids form very weak conjugate bases (e.g., $\mathrm{Cl}^{-}, \mathrm{NO}_3^{-}$).
- Strong bases form very weak conjugate acids.
- Weak acids (e.g., $\mathrm{CH}_3 \mathrm{COOH}$, HF) only partially dissociate and have strong conjugate bases.
Indicators like phenolphthalein and bromothymol blue are weak acids that change color based on the pH, useful in acid-base titrations.
Ionic Product of Water
Water molecules, for example, have the unique ability to operate as both an acid and a base
Water's concentration is ignored in the denominator because it is a pure liquid with a constant concentration. The Ionic Product of Water, Kw, is then equal to the equilibrium constant.
$K_{\mathrm{w}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]$
We can distinguish acidic, neutral and basic aqueous solutions by the relative values of the $\mathrm{H}_3 \mathrm{O}^{+}$and $\mathrm{OH}^{-}$concentrations:
Acidic: $\left[\mathrm{H}_3 \mathrm{O}^{+}\right]>\left[\mathrm{OH}^{-}\right]$
Neutral: $\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]$
Basic : $\left[\mathrm{H}_3 \mathrm{O}^{+}\right]<\left[\mathrm{OH}^{-}\right]$
pH Scale
The pH scale is used to determine the nature of any substance. The negative logarithm of hydrogen ion concentration is used to calculate the pH of a solution.
$\mathrm{pH}=-\log \mathrm{a}_{\mathrm{H}^{+}}=-\log \left\{\left[\mathrm{H}^{+}\right] / \operatorname{mol~L} \mathrm{L}^{-1}\right\}$
The acidic or basic strength of a solution is measured by its pH
On pH scale, up to 7 is acidic, at 7 it is neutral, and above 7 it is basic.
Ionization Constants of Weak Acids
Waek acids partially ionize in the aqeous solutions. Equilibrium constant for the acid-dissociation equilibrium:
$
K_{\mathrm{a}}=\mathrm{c}^2 \alpha^2 / \mathrm{c}(1-\alpha)=\mathrm{c} \alpha^2 / 1-\alpha
$
$K_{\mathrm{a}}$ is called the dissociation or ionization constant of acid HX. It can be represented alternatively in terms of molar concentration as follows,
$
K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right] /[\mathrm{HX}]
$
The Ionization Constants of Some Selected Weak Acids (at 298K) are given below:
| Acid | Ka (at 298K) |
|---|---|
| Hydrofluoric Acid (HF) | $3.5 \times 10^{-4}$ |
| Nitrous Acid ($\mathrm{HNO}_2$) | $4.5 \times 10^{-4}$ |
| Formic Acid (HCOOH) | $1.8 \times 10^{-4}$ |
| Niacin ($\mathrm{C}_5 \mathrm{H}_4 \mathrm{NCOOH}$) | $1.5 \times 10^{-5}$ |
| Acetic Acid ($\mathrm{CH}_3 \mathrm{COOH}$) | $1.74 \times 10^{-5}$ |
| Benzoic Acid ($\mathrm{C}_6 \mathrm{H}_5 \mathrm{COOH}$) | $6.5 \times 10^{-5}$ |
| Hypochlorous Acid (HClO) | $3.0 \times 10^{-8}$ |
| Hydrocyanic Acid (HCN) | $4.9 \times 10^{-10}$ |
| Phenol ($\mathrm{C}_6 \mathrm{H}_5 \mathrm{OH}$) | $1.3 \times 10^{-10}$ |
Concise Steps to Calculate pH of a Weak Electrolyte:
-
Identify Brønsted-Lowry acid/base species before dissociation.
-
Write balanced equations for all possible acid-base reactions.
-
Select the primary reaction based on the higher Ka value.
-
Tabulate initial, change (using α), and equilibrium concentrations for the primary reaction.
-
Substitute into the Ka expression and solve for α (degree of ionization).
-
Calculate equilibrium concentrations.
-
Determine pH using: pH = –log[$\mathrm{H}_3 \mathrm{O}^{+}$].
Ionization of Weak Bases
The ionization of base MOH can be represented by equation:
$
\mathrm{MOH}(\mathrm{aq}) \rightleftharpoons \mathrm{M}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})
$
In a weak base there is partial ionization of MOH into $\mathrm{M}^{+}$and $\mathrm{OH}^{-}$, the case is similar to that of acid-dissociation equilibrium. The equilibrium constant for base ionization is called base ionization constant and is represented by $K_{\mathrm{b}}$.
When equilibrium is reached, the equilibrium constant can be written as:
$
K_b=(c \alpha)^2 / c(1-\alpha)=c \alpha^2 /(1-\alpha)
$
Relation between $K_{\mathrm{a}}$ and $K_{\mathrm{b}}$
Ka and Kb represent the strength of an acid and a base, respectively. In case of a conjugate acid-base pair, they are related in a simple manner so that if one is known, the other can be deduced.
$K_{\mathrm{a}} \times K_{\mathrm{b}}=K_{\mathrm{w}}$
Di- and Polybasic Acids and Di-and Polyacidic Bases
Some of the acids like oxalic acid, sulphuric acid and phosphoric acids have more than one ionizable proton per molecule of the acid. Such acids are known as polybasic or polyprotic acids.
The ionization reactions for example for a dibasic acid $\mathrm{H}_2 \mathrm{X}$ are represented by the equations:
$
\begin{aligned}
& \mathrm{H}_2 \mathrm{X}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{HX}^{-}(\mathrm{aq}) \\
& \mathrm{HX}^{-}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{X}^{2-}(\mathrm{aq})
\end{aligned}
$
And the corresponding equilibrium constants are given below:
$
K_{a_1}=\left\{\left[\mathrm{H}^{+}\right]\left[\mathrm{HX}^{-}\right]\right\} /\left[\mathrm{H}_2 \mathrm{X}\right] \text { and }
$
$
K_{\mathrm{a}_2}=\left\{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^2-\right]\right\} /\left[\mathrm{HX}^{-}\right]
$
Here, $K_{\mathrm{a}_1}$ and $K_{\mathrm{a}_2}$ are called the first and second ionisation constants, respectively, of the acid $\mathrm{H}_2$ and X.
Factors Affecting Acid Strength
The strength of an acid depends mainly on the polarity and bond strength of the H–A bond:
-
Weaker H–A bond → easier to break → stronger acid
-
More polar H–A bond → greater charge separation → easier dissociation → stronger acid
Group trend (↓ group):
-
Bond strength dominates
-
Larger A → weaker H–A bond → stronger acid
e.g., HF < HCl < HBr < HI
Period trend (→ across a period):
-
Polarity (electronegativity) dominates
-
More electronegative A → more polar H–A bond → stronger acid
e.g., $\mathrm{CH}_4<\mathrm{NH}_3<\mathrm{H}_2 \mathrm{O}<\mathrm{HF}$
Also, $\mathrm{H}_2 \mathrm{~S}$ is stronger than $\mathrm{H}_2 \mathrm{O}$ due to a weaker S–H bond compared to O–H.
Common Ion Effect
The process reverses direction due to an increase in acetate ions. That is, it prevents acetic acid from dissociating. This is referred to as the common ion effect. It can be defined as "the suppression of acid ionisation when a substance containing a common ion is added to it."
Consider an example of acetic acid dissociation equilibrium represented as:
$
\begin{aligned}
& \mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq}) \\
& \text { or } \mathrm{HAc}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{Ac}^{-}(\mathrm{aq}) \\
& K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{Ac}^{-}\right] /[\mathrm{HAc}]
\end{aligned}
$
Addition of acetate ions to an acetic acid solution results in a decrease in the concentration of hydrogen ions, [H+]. Also, if H+ ions are added from an external source, then the equilibrium moves in the direction of undissociated acetic acid i.e., in a direction of reducing the concentration of hydrogen ions, [H+].
Hydrolysis of Salts and the pH of their Solutions
Salts formed from acids and bases ionize in water, and their ions may undergo hydrolysis, affecting the pH.
1. Salts of Strong Acid + Strong Base (e.g., NaCl):
- No hydrolysis occurs.
- $\mathrm{pH}=7$ (neutral).
2. Salts of Weak Acid + Strong Base (e.g., $\mathrm{CH}_3 \mathrm{COONa}$ ):
- Anion $\left(\mathrm{CH}_3 \mathrm{COO}^{-}\right)$hydrolyzes to produce $\mathbf{O H}^{-}$.
- Solution becomes basic, pH > 7.
3. Salts of Strong Acid + Weak Base (e.g., $\mathrm{NH}_4 \mathrm{Cl}$ ):
- Cation $\left(\mathrm{NH}_4{ }^{+}\right)$hydrolyzes to produce $\mathbf{H}^{+}$.
- Solution becomes acidic, pH < 7.
4. Salts of Weak Acid + Weak Base (e.g., $\mathrm{CH}_3 \mathrm{COONH}_4$ ):
- Both ions hydrolyse.
- pH depends on the relative strengths of acid and base:
$
\mathrm{pH}=7+\frac{1}{2}\left(\mathrm{p} K_a-\mathrm{p} K_b\right)
$
- If pKa > pKb, pH > 7 (basic)
- If pKa < pKb, pH < 7 (acidic)
The degree of hydrolysis in weak acid-weak base salts is independent of concentration.
Buffer Solutions
Many physiological fluids, such as blood or urine, have a specific pH, and any variation from this shows that the body is malfunctioning. Controlling pH is also crucial in a variety of chemical and biological activities. Many medical and cosmetic compositions demand that they be stored and delivered at a specific temperature and a specific pH. Buffer Solutions are resistant solutions that resist pH change.
Designing Buffer Solution
To prepare a buffer of acidic pH we use weak acid and its salt formed with strong base. We develop the equation relating the pH , the equilibrium constant, $K_a$ of weak acid and ratio of concentration of weak acid and its conjugate base. For the general case where the weak acid HA ionises in water,
$
\mathrm{HA}+\mathrm{H}_2 \mathrm{O} \leftrightharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{A}^{-}
$
For which we can write the expression
$
K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}
$
Rearranging the expression we have,
$
\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=K_a \frac{[\mathrm{HA}]}{\left[\mathrm{A}^{-}\right]}
$
Taking logarithm on both the sides and rearranging the terms we get -
$
\mathrm{p} K_a=\mathrm{pH}-\log \frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}
$
Or
$
\begin{gathered}
\mathrm{pH}=\mathrm{p} K_a+\log \frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]} \\
\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\text { Conjugate base, } \mathrm{A}^{-}\right]}{[\text {Acid, } \mathrm{HA}]}
\end{gathered}
$
The expression is known as the Henderson-Hasselbalch equation. The quantity $\frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}$ is the ratio of concentration of the conjugate base (anion) of the acid and the acid present in the mixture.
Solubility Equilibria of Sparingly Soluble Salts
The solubility depends on a number of factors, important amongst which are the lattice enthalpy of the salt and the solvation enthalpy of the ions in a solution. For a salt to dissolve in a solvent, the strong forces of attraction between its ions (lattice enthalpy) must be overcome by the ion-solvent interactions. The solvation enthalpy of ions is referred to in terms of solvation, which is always negative, i.e. energy is released in the process of solvation. The amount of solvation enthalpy depends on the nature of the solvent. In case of a nonpolar (covalent) solvent, the solvation enthalpy is small and hence, not sufficient to overcome lattice enthalpy of the salt.
Solubility Product Constant
The equilibrium between the undisolved solid and the ions in a saturated solution can be represented by the equation:
$\mathrm{BaSO}_4(\mathrm{~s}) \underset{\text { in water }}{\stackrel{\text { Saturated Solution }}{\rightleftharpoons}} \mathrm{Ba}^{2+}(\mathrm{aq})+\mathrm{SO}_4^{2-}(\mathrm{aq})$,
The equilibrium constant is given by the equation:
$
K=\left\{\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{SO}_4^{2-}\right]\right\} /\left[\mathrm{BaSO}_4\right]
$
For a pure solid substance, the concentration remains constant, and we can write
$
K_{\mathrm{sp}}=\mathrm{K}\left[\mathrm{BaSO}_4\right]=\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{SO}_4^{2-}\right]
$
We call $K_{\mathrm{sp}}$ the solubility product constant or simply the solubility product.
A solid salt of the general formula $\mathrm{M}_{\mathrm{x}}^{\mathrm{p}+} \mathrm{X}_{\mathrm{y}}^{\mathrm{q}-}$ with molar solubility S in equilibrium with its saturated solution may be represented by the equation:
$
\begin{aligned}
& \mathrm{M}_{\mathrm{x}} \mathrm{X}_{\mathrm{y}}(\mathrm{~s}) \rightleftharpoons \mathrm{xM}^{\mathrm{p}^{+}}(\mathrm{aq})+\mathrm{yX}^{\mathrm{q}^{-}}(\mathrm{aq}) \\
& \left(\text { where } \mathrm{x} \times \mathrm{p}^{+}=\mathrm{y} \times \mathrm{q}^{-}\right)
\end{aligned}
$
And its solubility product constant is given by:
$
\begin{aligned}
K_{\mathrm{sp}} & =\left[\mathrm{M}^{\mathrm{p}+}\right]^{\mathrm{x}}\left[\mathrm{X}^{\mathrm{q}-}\right]^{\mathrm{y}}=(\mathrm{xS})^{\mathrm{x}}(\mathrm{yS})^{\mathrm{y}} \\
& =\mathrm{x}^{\mathrm{x}} \cdot \mathrm{y}^{\mathrm{y}} \cdot \mathrm{~S}^{(\mathrm{x}+\mathrm{y})} \\
& \mathrm{S}^{(\mathrm{x}+\mathrm{y})}=K_{\mathrm{sp}} / \mathrm{x}^{\mathrm{x}} \cdot \mathrm{y}^{\mathrm{y}} \\
\mathrm{~S}= & \left(K_{\mathrm{sp}} / \mathrm{x}^{\mathrm{x}} \cdot \mathrm{y}^{\mathrm{y}}\right)^{1 / \mathrm{x}+\mathrm{y}}
\end{aligned}
$
The term $K_{\mathrm{sp}}$ in equation is given by $Q_{\mathrm{sp}}$ (section 6.6.2) when the concentration of one or more species is not the concentration under equilibrium. Obviously under equilibrium conditions $K_{\mathrm{sp}}=Q_{\mathrm{sp}}$ but otherwise it gives the direction of the processes of precipitation or dissolution.
Common Ion Effect on Solubility of Ionic Salts
According to Le Chatelier's Principle:
- Adding a common ion $\rightarrow$ shifts equilibrium to reduce ion concentration $\rightarrow$ precipitation increases until Ksp = Qsp.
- Removing an ion $\rightarrow$ more salt dissolves to restore equilibrium.
- Example: Passing HCl gas into saturated NaCl solution increases $\mathrm{Cl}^{-}$concentration $\rightarrow \mathbf{N a C l}$ precipitates (high-purity salt via common ion effect).
Applications:
- Used in gravimetric analysis to precipitate ions like:
- $\mathrm{Ag}^{+}$as AgCl
- $\mathrm{Fe}^{3+}$ as $\mathrm{Fe}(\mathrm{OH})_3$
- $\mathrm{Ba}^{2+}$ as $\mathrm{BaSO}_4$
Effect of pH on Solubility:
- For salts of weak acids (e.g., phosphates), solubility increases at low pH because:
- Anion (e.g., $\mathrm{PO}_4{ }^{3-}$ ) gets protonated, lowering its concentration.
- To maintain Ksp = Qsp, more salt dissolves.
Quantitatively:
$
S=\sqrt{\frac{K_{s p}\left(\left[\mathrm{H}^{+}\right]+K_a\right)}{K_a}}
$
As [ $\mathrm{H}^{+}$] increases (i.e., pH decreases), S increases.
Thus, the common ion effect reduces solubility, while lowering pH can increase solubility for salts of weak acids.
Equilibrium Previous Years Questions and Answers
Practicing these previous year questions will help you understand the exam pattern and the type of questions asked. These are useful for strengthening your preparation and improving accuracy. The concepts used to solve these questions are explained in ncert class 11 chemistry chapter 6 equilibrium notes.
Question: An aqueous solution of HCl with pH 1.0 is diluted by adding an equal volume of water (ignoring dissociation of water). The pH of HCl solution would
(Given $\log 2=0.30$ )
(1) reduce to 0.5
(2) increase to 1.3
(3) remain same
(4) increase to 2
Answer: $\mathrm{HCl}_{(\mathrm{aq})} \mathrm{pH}=1 ;\left[\mathrm{H}^{+}\right]=10^{-1}$
If equal volume of water is added concentration will become half
$\begin{aligned}
& {\left[\mathrm{H}^{+}\right]_{\text {sol }}=\frac{10^{-1}}{2}} \\
& \mathrm{pH}=1.3
\end{aligned}$
Hence, the correct answer is option (2).
Question: In the following system, $\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})$ at equilibrium, upon addition of xenon gas at constant $T \& p$, the concentration of
(1) $\mathrm{PCl}_5$ will increase
(2) $\mathrm{Cl}_2$ will decrease
(3) $\mathrm{PCl}_5, \mathrm{PCl}_3 \& \mathrm{Cl}_2$ remain constant
(4) $\mathrm{PCl}_3$ will increase
Answer: Addition of xenon gas, an inert gas, to the equilibrium system $\mathrm{PCl}_5(\mathrm{~g}) \leftrightharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})$ at a constant temperature and pressure, it affects the equilibrium according to Le Chatelier's principle. The addition of an inert gas at constant pressure effectively increases the volume of the system, reducing the concentration of the gases involved.
Since the system is at constant pressure, adding an inert gas increases the total volume, which favours the side of the reaction with more moles of gas. In this reaction, there are two moles of gas on the right side $\left(\mathrm{PCl}_3\right.$ and $\left.\mathrm{Cl}_2\right)$ compared to one mole on the left $\left(\mathrm{PCl}_5\right)$. Thus, the equilibrium will shift toward the right to increase the number of moles and counteract the change, decreasing the concentration of $\mathrm{PCl}_5$ and increasing the concentrations of $\mathrm{PCl}_3$ and $\mathrm{Cl}_2$.
Hence, the correct answer is option (4).
Question: When hydrochloric acid is added to cobalt nitrate solution at room temperature, the following reaction takes place, and the reaction mixture becomes blue. On cooling the mixture, it becomes pink. On the basis of this information, mark the correct answer.
$\left[\mathrm{Co}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{3+}(\mathrm{aq})+4 \mathrm{Cl}^{-}(\mathrm{aq}) \rightleftharpoons\left[\mathrm{CoCl}_4\right]^{2-}(\mathrm{aq})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l})$
- ΔH > 0 for the reaction
- ΔH < 0 for the reaction
- ΔH = 0 for the reaction
- The sign of ΔH cannot be predicted on the basis of this information.
Answer: (1) $\Delta H>0$ for the reaction
Explanation: On the cooling of the mixture, the reaction tends to move towards the backwards direction, which is an endothermic reaction, and, hence, $\Delta H>0$.
Hence, the answer is option (1).
How to Master Class 11 Chemistry Chapter 6 Equilibrium
The class 11 chemistry chapter 6 equilibrium notes explains how chemical reactions reach a balance between forward and backward processes. These notes help to understand the basic concepts from your NCERT textbook. Given below some points on how to master this chapter.
- Students must understand the basic concepts first like law of mass action and derivation of the equilibrium constant (Kc, Kp).
- Then learn about the relationship between Kc and Kp, Le Chatelier’s principle and Haber process.
- Questions related to concepts like ionic equilibrium concepts, pH, pOH, buffer action, solubility product (Ksp), and common ion effect are often asked in exams. To understand these concepts well students can refer to equilibrium class 11 chemistry chapter 6 CBSE notes.
- Then students must solve questions on topics like equilibrium constant, solubility, and pH calculations.
- At last students can solve previous year questions from this chapter.
NCERT Class 11 Notes Chapter-Wise
Along with chapter 6 equilibrium notes, you can also refer to the NCERT notes for all other Class 11 chapters provided below.
NCERT Solutions for Class 11 Chemistry
Along with equilibrium class 11 chemistry chapter 6 CBSE notes, follow the links below to get chapter-wise solutions of NCERT and make your learning better.
Subject-Wise NCERT Exemplar Solutions
Students can refer to the links given below for subject-wise NCERT Exemplar Solutions
Subject-Wise NCERT Solutions
Students can refer to the links given below for subject-wise NCERT Solutions
| NCERT Solutions for Class 11 Mathematics |
| NCERT Solutions for Class 11 Chemistry |
| NCERT Solutions for Class 11 Physics |
| NCERT Solutions for Class 11 Biology |
Frequently Asked Questions (FAQs)
Q: Are all topics covered in Class 11 Chemistry Equilibrium notes?
A:
Yes, comprehensive Class 11 Chemistry Equilibrium notes cover all key topics, including reversible reactions, law of mass action, equilibrium constants (Kc and Kp), Le Chatelier’s principle, ionic equilibrium, buffer solutions, solubility product, and common ion effect. They also include formulas, examples, and practice questions for complete exam preparation.
Q: What is equilibrium in Class 11 chemistry?
A:
Equilibrium in chemistry refers to a state in a reversible chemical reaction where the rates of the forward and reverse reactions are equal, so the concentrations of reactants and products remain constant over time.
Q: What is equilibrium class 11 chemistry chapter 6 CBSE notes?
A:
NCERT Class 11 Chemistry Chapter 6 Notes Equilibrium for the CBSE board are concise study materials summarising key concepts of Chapter 6, including law of mass action, equilibrium constants, Le Chatelier’s principle, and ionic equilibrium. These notes include definitions, formulas, solved examples, and important tips to help students revise quickly and prepare efficiently for exams.
Q: How do I Revise Class 11 chemistry equilibrium notes?
A:
Q: What is Reaction quotient ?
A:
The ratio of the molar concentrations of the products to those of the reactants for any reversible reaction at any point other than equilibrium. The reaction quotient is the product of each concentration term being raised to the power of the stoichiometric coefficient for the substance in concern.
Q: What is ionic equilibrium?
A:
Ionic equilibrium is when the rates of forward and reverse ionic reactions are equal, resulting in constant ion concentrations in a solution.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters