NCERT Solutions for Miscellaneous Exercise Chapter 12 Class 12

Q: How many exercises in NCERT Class 12 chapter 12 linear programming?

There are three exercises including miscellaneous exercises.

Q: What is the number of questions discussed in the NCERT solutions for Class 12 Maths chapter 12 miscellaneous exercise?

Ten questions are covered in Class 12 Maths chapter 12 miscellaneous solutions

Q: What is the expected number of questions from the chapter linear programming for the CBSE Class 12 Maths board exam?

One question of 5 marks can be expected

Q: What are the types of linear programming problems discussed in the Class 12 chapter linear programming.?

Diet, manufacturing and transportation problems are discussed before the ncert solutions for Class 12 Maths chapter 12 miscellaneous exercise.

Q: What are constraints?

Constraints are rules or conditions that are used in optimization problems

NCERT Solutions for Miscellaneous Exercise Chapter 12 Class 12 - Linear Programming

Edited By Ramraj Saini | Updated on Dec 04, 2023 01:54 PM IST | #CBSE Class 12th

NCERT Solutions For Class 12 Chapter 12 Miscellaneous Exercise

NCERT Solutions for miscellaneous exercise chapter 12 class 12 Linear Programming are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. NCERT solutions for Class 12 Maths chapter 12 miscellaneous exercise gives more knowledge of solving a few types of linear programming problems using graphical methods. Miscellaneous exercise chapter 12 Class 12 are solved in a detailed manner with necessary steps and graphs. Going through NCERT solutions for Class 12 Maths chapter 12 miscellaneous exercise gives a better understanding of the linear programming problems. The questions discussed in the NCERT book Class 12 Maths chapter 12 miscellaneous solutions are a bit higher level as compared to the other two exercises. Class 12 Maths chapter 12 miscellaneous solutions are important for C lass 12 CBSE Board Exams.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

This Story also Contains

NCERT Solutions For Class 12 Chapter 12 Miscellaneous Exercise
More About NCERT Solutions for Class 12 Maths Chapter 12 Miscellaneous Exercise:
Benefits of NCERT Solutions for Class 12 Maths Chapter 12 Miscellaneous Exercise.
Key Features Of NCERT Solutions For Class 12 Chapter 12 Miscellaneous Exercise
Also see-
NCERT Solutions Subject Wise
Subject Wise NCERT Exemplar Solutions

Miscellaneous exercise class 12 chapter 12 are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise enumerated in NCERT Book together using the link provided below.

VMC VIQ Scholarship Test

Apply

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

Apply

Linear Programming Class 12 Chapter 12-Miscellaneous Exercise

Question:1 Reference of Example 9 (Diet problem): A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

How many packets of each food should be used to maximise the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?

Answer:

Let diet contain x packets of food P and y packets of food Q. Thus, $x\geq 0,y\geq 0$ .

The mathematical formulation of the given problem is as follows:

Total cost is Z . $Z=6x+3y$

Subject to constraint,

$4x+y\geq 80$

$x+5y\geq 115$

$x\geq 0,y\geq 0$

The feasible region determined by constraints is as follows:

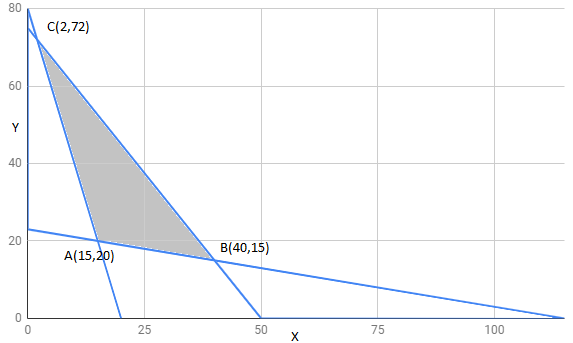
1627377546036

The corner points of feasible region are $A(15,20),B(40,15),C(2,72)$

The value of Z at corner points is as shown :

corner points	$Z=6x+3y$
$A(15,20)$	150	MINIMUM
$B(40,15)$	285	maximum
$C(2,72)$	228

Hence, Z has a maximum value of 285 at the point $B(40,15)$ .

to maximise the amount of vitamin A in the diet, 40 packets of food P and 15 packets of food Q should be used. The maximum amount of vitamin A is 285 units.

Question:2 A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?

Answer:

Let farmer mix x bags of brand P and y bags of brand Q. Thus, $x\geq 0,y\geq 0$ .

The given information can be represented in the table as :

	Vitamin A	Vitamin B	Cost
Food P	3	5	60
Food Q	4	2	80
requirement	8	11

The given problem can be formulated as follows:

Therefore, we have

$3x+1.5y\geq 18$

$2.5x+11.25y\geq 45$

$2x+3y\geq 24$

$Z=250x+200y$

Subject to constraint,

$3x+1.5y\geq 18$

$2.5x+11.25y\geq 45$

$2x+3y\geq 24$

$x\geq 0,y\geq 0$

The feasible region determined by constraints is as follows:

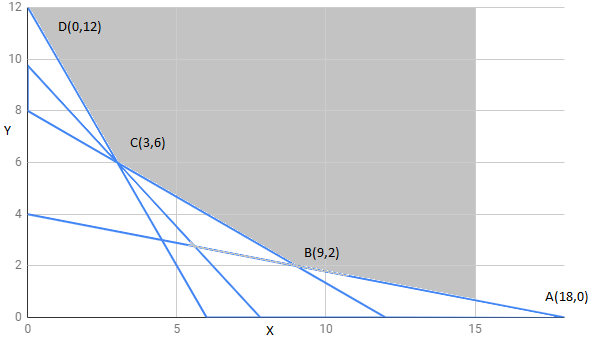
1627377686090

The corner points of the feasible region are $A(18,0),B(9,2),C(3,6),D(0,12)$

The value of Z at corner points is as shown :

corner points	$Z=250x+200y$
$A(18,0)$	4500
$B(9,2)$	2650
$C(3,6)$	1950	minimum
$D(0,12)$	2400

Feasible region is unbounded, therefore 1950 may or may not be a minimum value of Z. For this, we draw $250x+200y< 1950$ and check whether resulting half plane has a point in common with the feasible region or not.

We can see a feasible region has no common point with $250x+200y< 1950$ .

Hence, Z has a minimum value 1950 at point $C(3,6)$ .

Question:3 A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:

Food	Vitamin A	Vitamin B	Vitamin C
X	1	2	3
Y	2	2	1

One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?

Answer:

Let mixture contain x kg of food X and y kg of food Y.

Mathematical formulation of given problem is as follows:

Minimize : $z=16x+20y$

Subject to constraint ,

$x+2y\geq 10$

$x+y\geq 6$

$3x+y\geq 8$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

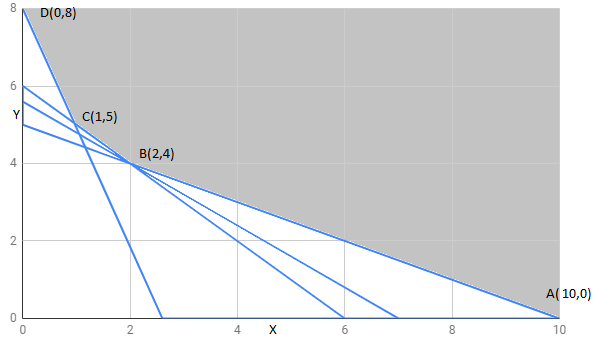
1627377734165

The corner points of feasible region are $A(10,0),B(2,4),C(1,5),D(0,8)$

The value of Z at corner points is as shown :

corner points	$z=16x+20y$
$A(10,0)$	160
$B(2,4)$	112	minimum
$C(1,5)$	116
$D(0,8)$	160

The feasible region is unbounded , therefore 112 may or may not be minimum value of Z .

For this we draw $16x+20y< 112$ and check whether resulting half plane has point in common with feasible region or not.

We can see feasible region has no common point with $16x+20y< 112$ .

Hence , Z has minimum value 112 at point $B(2,4)$

Question:4 A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

Types of toys	Machines
Types of toys	I	II	III
A	12	18	6
B	6	0	9

Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.

Answer:

Let x and y toys of type A and type B.

Mathematical formulation of given problem is as follows:

Minimize : $z=7.5x+5y$

Subject to constraint ,

$2x+y\leq 60$

$x\leq 20$

$2x+3y \leq 120$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

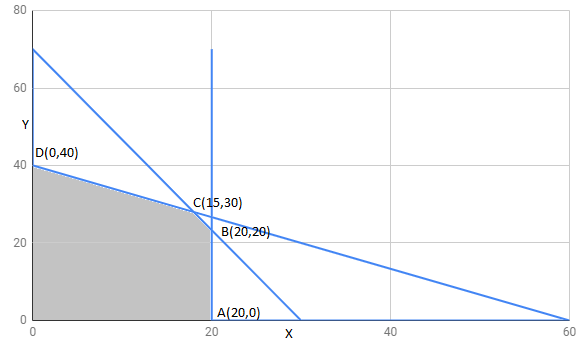
1627377785282

The corner points of feasible region are $A(20,0),B(20,20),C(15,30),D(0,40)$

The value of Z at corner points is as shown :

corner points	$z=7.5x+5y$
$A(20,0)$	150
$B(20,20)$	250
$C (15,30)$	262.5	maximum
$D(0,40)$	200

Therefore 262.5 may or may not be maximum value of Z .

Hence , Z has maximum value 262.5 at point $C (15,30)$

Question:5 An aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?

Answer:

Let airline sell x tickets of executive class and y tickets of economy class.

Mathematical formulation of given problem is as follows:

Minimize : $z=1000x+600y$

Subject to constraint ,

$x+y\leq 200$

$x\geq 20$

$y-4x\geq 0$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

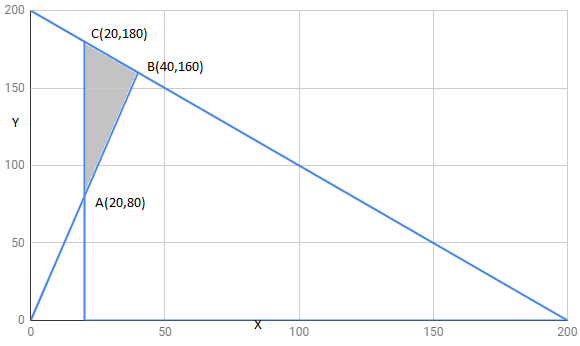
1627377831247

The corner points of feasible region are $A(20,80),B(40,160),C(20,180)$

The value of Z at corner points is as shown :

corner points	$z=1000x+600y$
$A(20,80)$	68000
$B(40,160)$	136000	maximum
$C (20,180)$	128000

therefore 136000 is maximum value of Z .

Hence , Z has maximum value 136000 at point $B(40,160)$

Question:6 Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:

Transportation cost per quintal (in Rs)
From/To	A	B
D	6	4
E	3	2
F	2.50	3

How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?

Answer:

Let godown A supply x and y quintals of grain to shops D and E respectively. Then , (100-x-y) will be supplied to shop F. Requirements at shop D is 60 since godown A supply x .Therefore remaining (60-x) quintals of grain will be transported from godown B.

Similarly, (50-y) quintals and 40-(100-x-y)=(x+y-60) will be transported from godown B to shop E and F respectively. The problem can be represented diagrammatically as follows:

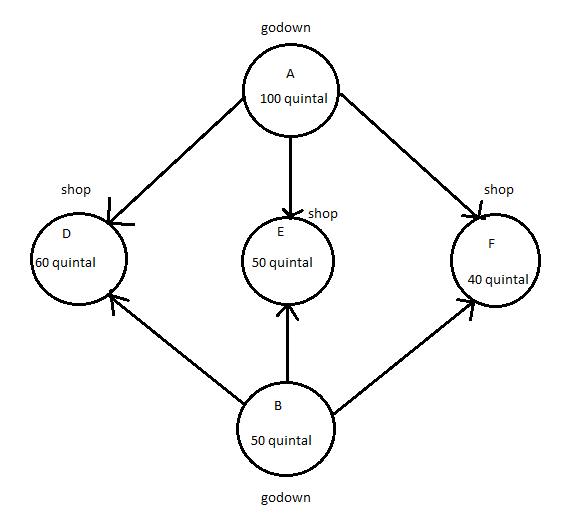
1627377923876

$x,y\geq 0$ and $100-x-y\geq 0$

$x,y\geq 0$ and $x+y\leq 100$

$60-x\geq 0,50-y\geq 0\, \, \, and\, \, x+y-60\geq 0$

$\Rightarrow \, \, \, \, x\leq 60,y\leq 50,x+y\geq 60$

Total transportation cost z is given by ,

$z=6x+3y+2.5(100-x-y)+4(60-x)+2(50-y)+3(x+y-60)$

$z=2.5x+1.5y+410$

Mathematical formulation of given problem is as follows:

Minimize : $z=2.5x+1.5y+410$

Subject to constraint ,

$x+y\leq 100$

$x\leq 60$

$y\leq 50$

$x+y\geq 60$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

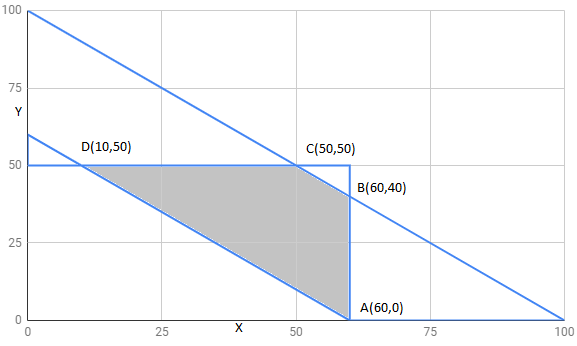
1627377885300

The corner points of feasible region are $A(60,0),B(60,40),C(50,50),D(10,50)$

The value of Z at corner points is as shown :

corner points	$z=2.5x+1.5y+410$
$A(60,0)$	560
$B(60,40)$	620
$C(50,50)$	610
$D(10,50)$	510	minimum

therefore 510 may or may not be minimum value of Z .

Hence , Z has miniimum value 510 at point $D(10,50)$

Question:7 An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:

Distance in (km.)
From/To	A	B
D	7	3
E	6	4
F	3	2

Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?

Answer:

Let x and y litres of oil be supplied from A to petrol pump,D and E. Then , (7000-x-y) will be supplied from A to petrol pump F.

Requirements at petrol pump D is 4500 L. since x L A are transported from depot A,remaining 4500-x L will be transported from petrol pump B

Similarly, (3000-y)L and 3500-(7000-x-y)=(x+y-3500) L will be transported from depot B to petrol E and F respectively.

The problem can be represented diagrammatically as follows:

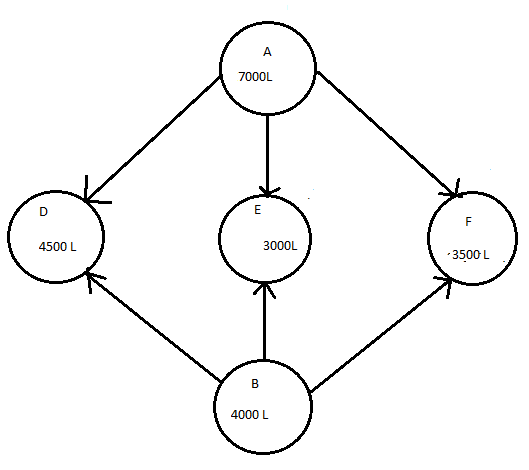
1627377981082

$x,y\geq 0$ and $7000-x-y\geq 0$

$x,y\geq 0$ and $x+y\leq 7000$

$4500-x\geq 0,3000-y\geq 0\, \, \, and\, \, x+y-3500\geq 0$

$\Rightarrow \, \, \, \, x\leq 4500,y\leq 3000,x+y\geq 3500$

Cost of transporting 10 L petrol =Re 1

Cost of transporting 1 L petrol $=\frac{1}{10}$

Total transportation cost z is given by ,

$z=\frac{7}{10}x+\frac{6}{10}y+\frac{3}{10}(7000-x-y)+\frac{3}{10}(4500-x)+\frac{4}{10}(3000-y)+\frac{2}{10}(x+y-3500)$

$z=0.3x+0.1y+3950$

Mathematical formulation of given problem is as follows:

Minimize : $z=0.3x+0.1y+3950$

Subject to constraint ,

$x+y\leq 7000$

$x\leq 4500$

$y\leq 3000$

$x+y\geq 3500$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

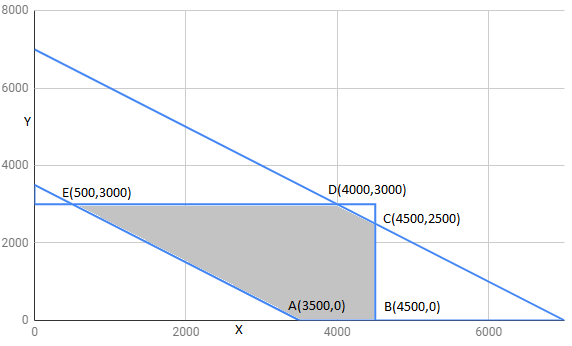
1627378013511

The corner points of feasible region are $A(3500,0),B(4500,0),C(4500,2500),D(4000,3000),E(500,3000)$

The value of Z at corner points is as shown :

corner points	$z=0.3x+0.1y+3950$
$A(3500,0)$	5000
$B(4500,0)$	5300
$C(4500,2500)$	5550
$E(500,3000)$	4400	minimum
$D(4000,3000)$	5450

Hence , Z has miniimum value 4400 at point $E(500,3000)$

Question:8 A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.

If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?

Kg per bag
	Brand P	Brand Q
Nitrogen	3	3.5
Phosphoric Acid	1	2
Potash	3	1.5
Chlorine	1.5	2

Answer:

Let fruit grower use x bags of brand P and y bags of brand Q.

Mathematical formulation of given problem is as follows:

Minimize : $z=3x+3.5y$

Subject to constraint ,

$x+2y\geq 240$

$x+0.5y\geq 90$

$1.5x+2y\geq 310$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

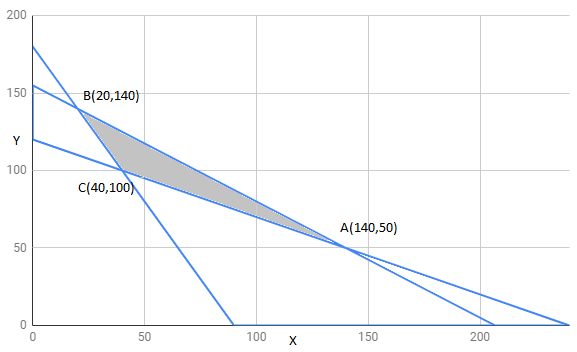
1627378058480

The corner points of feasible region are $A(140,50),C(40,100),B(20,140)$

The value of Z at corner points is as shown :

corner points	$z=3x+3.5y$
$A(140,50)$	595
$B(20,140)$	550
$C(40,100)$	470	minimum

Therefore 470 is minimum value of Z .

Hence , Z has minimum value 470 at point $C(40,100)$

Question:9 Reference of Que 8 : A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.

If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?

Kg per bag
	Brand A	Brand P
Nitrogen	3	3.5
Phosphoric Acid	1	2
Potash	3	1.5
Chlorine	1.5	2

Answer:

Let fruit grower use x bags of brand P and y bags of brand Q.

Mathematical formulation of given problem is as follows:

Maximize : $z=3x+3.5y$

Subject to constraint ,

$x+2y\geq 240$

$x+0.5y\geq 90$

$1.5x+2y\geq 310$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

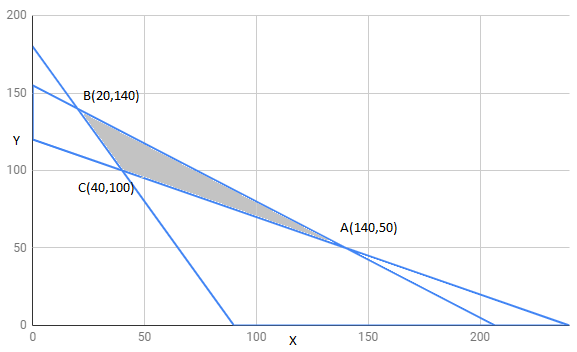
1627378216485

The corner points of feasible region are $B(20,140),A(140,50),C(40,100)$

The value of Z at corner points is as shown :

corner points	$z=3x+3.5y$
$A(140,50)$	595	maximum
$B(20,140)$	550
$C(40,100)$	470	minimum

therefore 595 is maximum value of Z .

Hence , Z has minimum value 595 at point $A(140,50)$

Question:10 A toy company manufactures two types of dolls, A and B. Market research and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs 12 and Rs 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximise the profit?

Answer:

Let x and y be number of dolls of type A abd B respectively that are produced per week.

Mathematical formulation of given problem is as follows:

Maximize : $z=12x+16y$

Subject to constraint ,

$x+y\leq 1200$

$y\leq \frac{x}{2}\Rightarrow x\geq 2y$

$x-3y\leq 600$

$x,y\geq 0$

The feasible region determined by constraints is as follows:

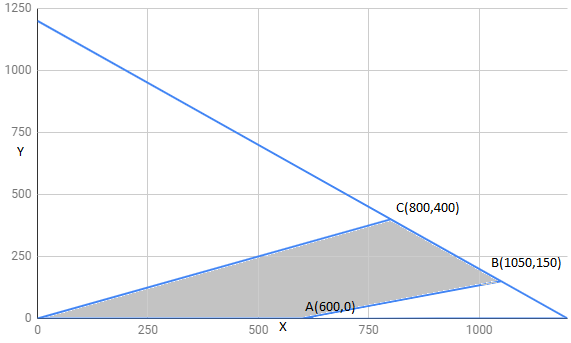
1627378272830

The corner points of feasible region are $A(600,0),B(1050,150),C(800,400)$

The value of Z at corner points is as shown :

corner points	$z=12x+16y$
$A(600,0)$	7200
$B(1050,150)$	15000
$C(800,400)$	16000	Maximum

Therefore 16000 is maximum value of Z .

Hence , Z has minimum value 16000 at point $C(800,400)$

Benefits of NCERT Solutions for Class 12 Maths Chapter 12 Miscellaneous Exercise.

Important questions to understand the concepts explained in the chapter are given in Class 12 Maths chapter 12 miscellaneous exercise solutions.
All questions of miscellaneous exercise chapter 12 Class 12 are important and will be helpful in the board exam.

Key Features Of NCERT Solutions For Class 12 Chapter 12 Miscellaneous Exercise

Comprehensive Coverage: The solutions encompass all the topics covered in miscellaneous exercise class 12 chapter 12, ensuring a thorough understanding of the concepts.
Step-by-Step Solutions: In this class 12 chapter 12 maths miscellaneous solutions, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
Accuracy and Clarity: Solutions for class 12 maths miscellaneous exercise chapter 12 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
Conceptual Clarity: In this class 12 maths ch 12 miscellaneous exercise solutions, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
Inclusive Approach: Solutions for class 12 chapter 12 miscellaneous exercise cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
Relevance to Curriculum: The solutions for miscellaneous exercise class 12 chapter 12 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. How many exercises in NCERT Class 12 chapter 12 linear programming?

There are three exercises including miscellaneous exercises.

2. What is the number of questions discussed in the NCERT solutions for Class 12 Maths chapter 12 miscellaneous exercise?

Ten questions are covered in Class 12 Maths chapter 12 miscellaneous solutions

3. What is the expected number of questions from the chapter linear programming for the CBSE Class 12 Maths board exam?

One question of 5 marks can be expected

4. The number of miscellaneous solved questions given in NCERT Class 12 Maths chapter linear programming is ………….

Three

5. What are the types of linear programming problems discussed in the Class 12 chapter linear programming.?

Diet, manufacturing and transportation problems are discussed before the ncert solutions for Class 12 Maths chapter 12 miscellaneous exercise.

6. What are constraints?

Constraints are rules or conditions that are used in optimization problems

Also Read

NCERT Class 12 Maths Notes - Download Chapter wise Free PDFs

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

Odisha Board Exam Date 2025 PDF - Check Odisha BSE CHSE Time Table Here

Nov 04, 2024

CHSE Odisha 2024 - Full Form, Exam Date, Syllabus, Results, Official Website

Nov 21, 2024

Odisha CHSE Exam Date 2025 Out, Check Odisha 12th Board Exam Time Table PDF!

Nov 21, 2024

CBSE Class 12 Computer Science Syllabus 2024-25: Download Syllabus PDF

Nov 21, 2024

CBSE Class 12 Biology Syllabus 2024-25 Download PDF Here

Nov 21, 2024

CBSE Class 12 Maths Syllabus 2024-25 Download Pdf: Chapterwise Weightage

Nov 21, 2024

CBSE Class 12 Chemistry Syllabus 2024-25 - Download PDF

Nov 21, 2024

CBSE Class 12 Exam Analysis 2025: Check Exam Analysis for All Subjects

Nov 21, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Mock Test

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Result

Mock Test

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Admit Card

Result

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

Exam Pattern

Result

Admit Card

View All School Exams

Certifications By Top Providers

Full-Stack Web Development

Via Masai School

Digital Banking Business Model

Via State Bank of India

Business Analytics Foundations

Via PW Skills

Master Data Management for Beginners

Via TCS iON Digital Learning Hub

Data Analytics Basics for Everyone

Via IBM

Banking 101 A Guide for Beginners in the Banking Sector

Via EduBridge

1113 courses

812 courses

394 courses

295 courses

Harvard University, Cambridge

98 courses

IBM

83 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

Environmental Studies

History

Artificial Intelligence

Psychology

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Delaware, Newark

Newark, DE 19716

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

PR in UK After Study for International and Indian Students 2025

9 min ⋆ Nov 14, 2024 13:11 PM IST

Duolingo English Test Accepting Universities and Countries in 2025-26

12 min ⋆ Nov 14, 2024 13:11 PM IST

Top MBA Colleges in Dubai 2025 (with Tuition fees): List of Best Colleges

11 min ⋆ Nov 14, 2024 13:11 PM IST

Cheapest Universities in Germany for International Students 2025-26

15 min ⋆ Nov 14, 2024 13:11 PM IST

Cheapest Universities in Melbourne 2025: Discover Affordable Education

7 min ⋆ Nov 14, 2024 13:11 PM IST

Top Courses to Study in USA for Indian and International Students 2025

11 min ⋆ Nov 14, 2024 13:11 PM IST

Related E-books & Sample Papers

CBSE Class 12 Accounts Sample Paper with Solution 2024-25 PDF

124+ Downloads

CBSE Class 12 Physical Education Sample Paper with Solution 2024-25 PDF

53+ Downloads

CBSE Class 12 Hindi Elective Sample Paper with Solution 2024-25 PDF

58+ Downloads

CBSE Class 12 Hindi Core Sample Paper with Solution 2024-25 PDF

53+ Downloads

CBSE Class 12 Political Science Sample Paper with Solution 2024-25 PDF

41+ Downloads

CBSE Class 12 Physics Sample Paper with Solution 2024-25 PDF

148+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer

Jefferson 25 September,2024

i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

Re-evaluate Your Study Strategies:
- Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
- Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
- Practice Regularly: Consistent practice is key to mastering chemistry.
Consider Professional Help:
- Tutoring: A tutor can provide personalized guidance and support.
- Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.
Explore Alternative Options:
- Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
- Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.
Focus on NEET 2025 Preparation:
- Stay Dedicated: Continue your NEET preparation with renewed determination.
- Utilize Resources: Make use of study materials, online courses, and mock tests.
Seek Support:
- Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
- Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.

Read Complete Answer

Kanishka kaushikii 17 September,2024

i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer

Yuvan 30 August,2024

i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer

Ashvadha 12 July,2024

Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer

kumardurgesh1802 10 July,2024

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Miscellaneous Exercise Chapter 12 Class 12 - Linear Programming

NCERT Solutions For Class 12 Chapter 12 Miscellaneous Exercise

VMC VIQ Scholarship Test

Pearson | PTE

More About NCERT Solutions for Class 12 Maths Chapter 12 Miscellaneous Exercise:

Benefits of NCERT Solutions for Class 12 Maths Chapter 12 Miscellaneous Exercise.

Key Features Of NCERT Solutions For Class 12 Chapter 12 Miscellaneous Exercise

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Certifications By Top Providers

Explore Top Universities Across Globe

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Popular CBSE Class 12th Questions

Colleges After 12th

VMC VIQ Scholarship Test

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

Stay up-to date with CBSE Class 12th News

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

NVS

JNVST

Schools By Medium

By Ownership

By City

By State

Download Careers360 App

All this at the convenience of your phone

Scan and download the app