NCERT Solutions for Class 12 Physics Chapter 14 - Semiconductor Electronics Materials Devices And Simple Circuit

Q. 14.1 In an n-type silicon, which of the following statement is true:

(a) Electrons are the majority carriers and trivalent atoms are the dopants.

(b) Electrons are minority carriers and pentavalent atoms are the dopants.

(c) Holes are minority carriers and pentavalent atoms are the dopants.

(d) Holes are majority carriers and trivalent atoms are the dopants.

Answer:

An n-type semiconductor has electrons as majority carriers and holes as minority carriers. It is formed when we dope a pentavalent impurity into a Silicon atom. Some pentavalent dopants are phosphorus, arsenic, and bismuth.

Hence, the correct option is C.

Q. 14.2 Which of the statements given in Exercise 14.1 is true for p-type semiconductors.

(a) Electrons are the majority carriers and trivalent atoms are the dopants.

(b) Electrons are minority carriers and pentavalent atoms are the dopants.

(c) Holes are minority carriers and pentavalent atoms are the dopants.

(d) Holes are majority carriers and trivalent atoms are the dopants

Answer:

In a p-type semiconductor, holes are the majority carrier and electrons are the minority carrier. It is formed when a trivalent atom-like aluminium is doped in a silicon atom. Hence correct option for p-type conductor would be (d).

Q. 14.3 Carbon, silicon and germanium have four valence electrons each. These are characterised by valence and conduction bands separated by energy bandgap respectively equal to $(E_{g})_{C},(E_{g})_{Si}$ and $(E_{g})_{Ge}$ . Which of the following statements is true?

(a) $(E_{g})_{Si} < (E_{g})_{Ge}< (E_{g})_{C}$

(b) $(E_{g})_{C} < (E_{g})_{Ge}> (E_{g})_{Si}$

(c) $(E_{g})_{C} > (E_{g})_{Si}> (E_{g})_{Ge}$

(d) $(E_{g})_{C} = (E_{g})_{Si}= (E_{g})_{Ge}$

Answer:

Since carbon is a non-metal, its energy band gap would be the highest and the energy band gap of Ge would be the least, as it is a metalloid.

$(E_{g})_{C} > (E_{g})_{Si}> (E_{g})_{Ge}$

Hence correct option would be (c)

Q14.4 In an unbiased p-n junction, holes diffuse from the p-region to n-region because

(a) free electrons in the n-region attract them,

(b) they move across the junction by the potential difference.

(c) hole concentration in the p-region is higher compared to the n-region.

d) All the above

Answer:

Charge flows from higher concentration to the lower concentration in a junction. In this case, holes are diffusing from the p-region to n-region and hence the concentration of hole is greater in the p-region.

and hence the correct option would be (c)

Q. 14.5 When a forward bias is applied to a p-n junction, it

(a) raises the potential barrier

(b) reduces the majority carrier current to zero.

(c) lowers the potential barrier.

(d) none of the above.

Answer:

When a p-n junction is forward biased, the negative voltage repels the electrons toward the junction and gives them the energy to cross the junction and combine with the holes which are also being pushed by a positive voltage. This leads to a reduction in the depletion layer, which means a reduction in the potential barrier across the junction.

Hence correct option would be (c)

Q. 14.6 In half-wave rectification, what is the output frequency if the input frequency is $50 \; Hz.$ What is the output frequency of a full-wave rectifier for the same input frequency

Answer:

As we know :

output frequency for half-wave rectifier = input frequency, and hence output frequency in half-wave rectifier will be 50Hz.

also, output frequency for full-wave rectifier = 2*(input frequency) and Hence output frequency in full-wave rectifier will be 2*50 = 100 Hz.

Q.2 The number of silicon atoms per m 3 is $5\times 10^{28}.$ This is doped simultaneously with $5\times 10^{22}.$ atoms per $m^{3}$ of Arsenic and $5\times 10^{20}$ per $m^{3}$ atoms of Indium. Calculate the number of electrons and holes. Given that $n_{i}=1.5\times 10^{16}\; m^{-3}.$ Is the material $n-type$ or $p-type$ ?

Answer:

Given:

number of Silicon atoms per $m^{3}$ = $5\times 10^{28}.$

number of Arsenic atoms per $m^{3}$ = $5\times 10^{22}.$

number of Indium atoms per $m^{3}$ = $5\times 10^{20}$

number of thermally generated electrons $n_{i}=1.5\times 10^{16}\; m^{-3}.$

Now,

Number of electrons

$n_e =$ $5 * 10 ^{22}-1.5*10^{16}$ = $4.99*10^{22}(approx)$

number of holes is $n_h$

in thermal equilibrium

$n_h*n_e=n_i^2$

$n_h=n_i^2/n_e$

$n_h= (1.5*10^{16})^2/4.99*10^{22}$

$n_h= 4.51 * 10^9$

Now, since the number of electrons is higher than number of holes, it is an n-type semiconductor.

Q.3 In an intrinsic semiconductor the energy gap $E_{g}$ is $1.2\; eV.$ Its hole mobility is much smaller than electron mobility and independent of temperature. What is the ratio between conductivity at $600K$ and that at $300K$ Assume that the temperature dependence of intrinsic carrier concentration $n_{i}$ is given by

$n_{i}=n_{0}\; exp\left [ -\frac{E_{g}}{2K_{B}T} \right ]$

Where, $n_{0}$ is constant.

Answer:

Energy gap of given intrinsic semiconductor = E g = 1.2eV

temperature dependence of intrinsic carrier concentration $n_{i}$ is given by

$n_{i}=n_{0}\; exp\left [ -\frac{E_{g}}{2K_{B}T} \right ]$

Where is constant, $K_B$ is Boltzmann constant = $8.862 * 10^{-5}eV/K$ ,

T is temperature

Initial temperature = T1 = 300K

The intrinsic carrier concentration at this temperature :

$n_{i1} = n_0exp[\frac{-E_g}{2K_B*300}]$

Final temperature = T2 = 600K

The intrinsic carrier concentration at this temperature :

$n_{i2} = n_0exp[\frac{-E_g}{2K_B*600}]$

The ratio between the conductivities at 300K and at 600K is equal to the ratio of their intrinsic carrier concentration at these temperatures

$\frac{n_{i2}}{n_{i2}} = \frac{n_0exp[\frac{-E_g}{2K_B*600}]}{n_0exp[\frac{-E_g}{2K_B*300}]}$

$= exp\frac{E_g}{2K_B}[\frac{1}{300}-\frac{1}{600}]=exp[\frac{1.2}{2*8.62*10^{-5}}* \frac{2-1}{600}]$

$= exp[11.6] = 1.09 * 10^{5}$

Therefore, the ratio between the conductivities is $1.09 * 10^{5}$.

Q.4 In a p-n junction diode, the current I can be expressed as

$I=I_{0}\; [exp \frac{eV}{K_{B}T}-1 ]$

where $I_{0}$ is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and $I$ is the current through the diode, $k_{B}$ is the Boltzmann constant $(8.6\times 10^{-5}eV/K)$ and $T$ is the absolute temperature. If for a given diode $I_{0}=5\times 10^{-12}A$ and $T=300\; K,$ then

What will be the forward current at a forward voltage of $0.6\; V\; ?$

Answer:

As we have

$I=I_{0}\; [exp \frac{eV}{K_{B}T}-1 ]$

Here, $I_{0}=5\times 10^{-12}A$ , $T=300\; K,$ and , $k_{B}$ = Boltzmann constant = $(8.6\times 10^{-5}eV/K)$ $=(1.376*10^{-23}J/K)$

When the forward voltage is 0.6V:

$I=5*10^{-12}\;[ exp \frac{1.6*10^{-19}*0.6}{1.376*10^{-23}*300}-1 ]=0.0625A$

Hence forward current is 0.0625A

Q.5 In a p-n junction diode, the current I can be expressed as

$I=I_{0}\; [exp \frac{eV}{K_{B}T}-1 ]$

where I0 is called the reverse saturation current, $V$ is the voltage across the diode and is positive for forward bias and negative for reverse bias, and $I$ is the current through the diode, $k_{B}$ is the Boltzmann constant $(8.6\times 10^{-5}\; eV/K)$ and $T$ is the absolute temperature. If for a given diode $I_{0}=5\times 10^{12}A$ and $T=300\; K,$ then

What will be the increase in the current if the voltage across the diode is increased to $0.7 \; V?$

Answer:

As we have

$I=I_{0}\; [exp \frac{eV}{K_{B}T}-1 ]$

Here, $I_{0}=5\times 10^{-12}A$ , $T=300\; K,$ and , $k_{B}$ = Boltzmann constant = $(8.6\times 10^{-5}eV/K)$ $=(1.376*10^{-23}J/K)$

When the forward voltage is 0.7V:

$I=5*10^{-12}\;[ exp \frac{1.6*10^{-19}*0.7}{1.376*10^{-23}*300}-1 ]=3.029A$

When the forward voltage is 0.6V:

$I=5*10^{-12}\;[ exp \frac{1.6*10^{-19}*0.6}{1.376*10^{-23}*300}-1 ]=0.0625A$

Hence the increase in the forward current is

$I(whenv=0.7) - I(whenv=.6)$ $= 3.029- 0.0625 = 2.967A$

Q.6 In a p-n junction diode, the current I can be expressed as

$I=I_{0}\; [exp \frac{eV}{K_{B}T}-1 ]$

where $I_{0}$ is called the reverse saturation current, $V$ is the voltage across the diode and is positive for forward bias and negative for reverse bias, and $I$ is the current through the diode, $k_{B}$ is the Boltzmann constant $(8.6\times 10^{-10}\; eV/K)$ and $T$ is the absolute temperature. If for a given diode $I_{0}=5\times 10^{-12}A$ and $T=300\; K,$ then

What is the dynamic resistance?

Answer:

Dynamic Resistance = $\frac{voltage-change}{ current-change}$

Resistance change = 0.7 - 0.6 = 0.1

Current change = 2.967(calculated in prev question)

Therefore

, $Dynamic Resistance = \frac{0.1}{2.967} = 0.0337\Omega$

Q.7 In a p-n junction diode, the current I can be expressed as

$I=I_{0}\; [exp \frac{eV}{K_{B}T}-1 ]$

where $I_{0}$ is called the reverse saturation current, $V$ is the voltage across the diode and is positive for forward bias and negative for reverse bias, and $I$ is the current through the diode, $k_{B}$ is the Boltzmann constant $(8.6\times 10^{-5}V/K)$ and $T$ is the absolute temperature. If for a given diode $I_{0}=5\times 10^{-12}A$ and $T=300\; K,$ then

What will be the current if the reverse bias voltage changes from 1 V to 2 V?

Answer:

As we have

$I=I_{0}\; [exp \frac{eV}{K_{B}T}-1 ]$

Here, $I_{0}=5\times 10^{-12}A$ , $T=300\; K,$ and , $k_{B}$ = Boltzmann constant = $(8.6\times 10^{-5}eV/K)$ $=(1.376*10^{-23}J/K)$

When reverse voltage is 1V, V= -1

$I=5*10^{-12}\;[ exp \frac{1.6*10^{-19}*(-1)}{1.376*10^{-23}*300}-1 ]\approx5\times10^{-12}$

When the reverse voltage is -2V:

$I=5*10^{-12}\;[ exp \frac{1.6*10^{-19}*(-2)}{1.376*10^{-23}*300}-1 ]\approx5\times10^{-12}$

In both case current is very small and approximately equal to the reverse saturation current, hence their difference is negligible which causes dynamic resistance of infinity.

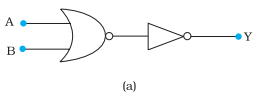
Q.8(a) You are given the two circuits as shown in Fig. Show that circuit acts as OR gate while the circuit

Answer:

Here, THE Input = A and B

Output = Y

The left part of the figure acts as a NOR and the right part acts as NOT Gate.

The output of NOR gate = $\overline{A+B}$

The output of the NOR gate would be the input of NOT Gate and hence

$\mathrm{Y}=\overline{\overline{A+B}}=\mathrm{A}+\mathrm{B}$

Hence the figure functions like an OR Gate.

Or compare the truth table by giving different inputs and observing the output

Q. 8(b) You are given the two circuits as shown in Fig. Show that circuit acts as AND gate.

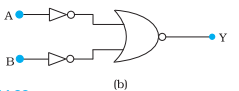
Answer:

The output of NOT gate ( left part of the circuit) is the input of the NOR gate

Hence the output of total circuit Y = $\over(\overline A + \overline B)$

= $\overline{\overline A}.\overline{\overline B}$ $\overline{A+B}=\overline A. \overline B$

= $A*B$

Hence the circuit functions as AND gate.

Or give the inputs 00,01,10,11 and observe the truth table

The truth table is the same as that of AND gate

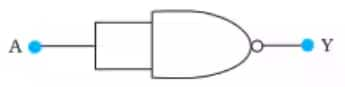
Q.9 Write the truth table for a NAND gate connected as given in the figure.

Hence identify the exact logic operation carried out by this circuit.

Answer:

Here, A is boththe input of the NAND gate and hence Output Y will be

$Y = \overline {A*A}$

$Y = \overline {A} + \overline A$

$Y = \overline {A}$

Hence circuit functions as a NOT gate.

The truth table for the given figure:

Q 10 You are given two circuits as shown in Fig, which consist of NAND gates. Identify the logic operation carried out by the two circuits.

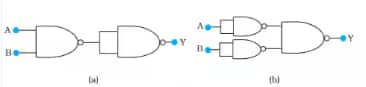
Answer:

a)

A and B are the inputs of a NAND gate and the output of this gate is the input of another NAND gate, so,

Y = $\over(\overline {A.B})(\overline {A.B})$

Y= $\over(\overline {A.B})$ $+$ $\over(\overline {A.B})$

Y= $AB$

Hence this circuit functions as AND gate.

b)

A is input to the NAND gate output of whose output goes to the rightmost NAND gate. Also, B is input to the NAND gate whose output goes to the rightmost NAND gate.

Y = $\over \overline A .\overline B$

Y = $\over\overline A .$ + $\over\overline B.$

Y = A + B

Hence, the circuit functions as an OR gate.

Alternative method

fig. a

Construct the truth table by giving various inputs and observing the output

The above truth table is the same as that of an AND gate

fig. b

The above truth table is the same as that of an OR gate

Q.11 Write the truth table for the circuit given in Fig below consisting of NOR gates and identify the logic operation (OR, AND, NOT) that this circuit is performing.

(Hint: $A=0,B=1$ then $A$ and $B$ inputs of second NOR gate will be $0$ and hence $Y=1.$ Similarly work out the values of $Y$ for other combinations of $A$ and $B.$ Compare with the truth table of OR, AND, NOT gates and find the correct one.)

Answer:

A and B are the input od a NOR gate and Output of this NOR gate is the Input of Another NOR gate whose Output is Y. Hence,

Y = $\over(\overline{A+B} + \overline{A+B})$

Y = $\over\overline {A+B}$ . $\over\overline {A+B}$

Y = A + B

Hence Circuit behaves as OR gate.

Truth table

Q.12 Write the truth table for the circuits given in Fig., consisting of NOR gates only. Identify the logic operations (OR, AND, NOT) performed by the two circuits.

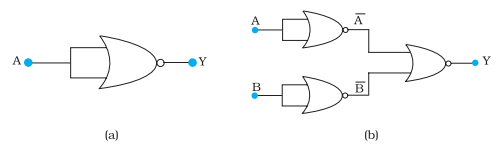
Answer:

a)

A is the two inputs of the NOR gate and hence, Output Y is:

Y = $\overline {A+A}$

Y = $\overline {A}$

Hence circuit functions as a NOT gate.

TRUTH TABLE:

b) A is the two inputs of a NOR gate whose output(which is $\overline {A}$ ) is the one input of another NOR gate. B is the two input of NOR gate whose output (which is $\overline {B}$ ) is the input of another NOR gate. Hence,

Y = $\over\overline {A} + \overline {B}$

Y = $\over\overline {A}$ . $\over\overline {B}$

Y = A.B

Hence it functions as AND gate.

TRUTH TABLE: