ALLEN Coaching
ApplyRegister for ALLEN Scholarship Test & get up to 90% Scholarship
Have you ever noticed the shape of satellite dishes, car headlights, or even the paths of planets? These shapes come from conic sections, a key topic in geometry. This chapter, conic sections, is a continuation of the last chapter of straight lines, and here we will discuss mainly four other curves: Circle, Hyperbola, Parabola, and Ellipse. “Conic” means “Cone” and “Sections” means “Intersection”. These curves are called “Conic sections” because they can be formed by the intersection of a plane with a double-napped right circular cone. Now, strengthening the basic concepts is necessary, and the NCERT Solutions will help to command the concepts.
New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes
JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy
Suggested: JEE Main: high scoring chapters | Past 10 year's papers
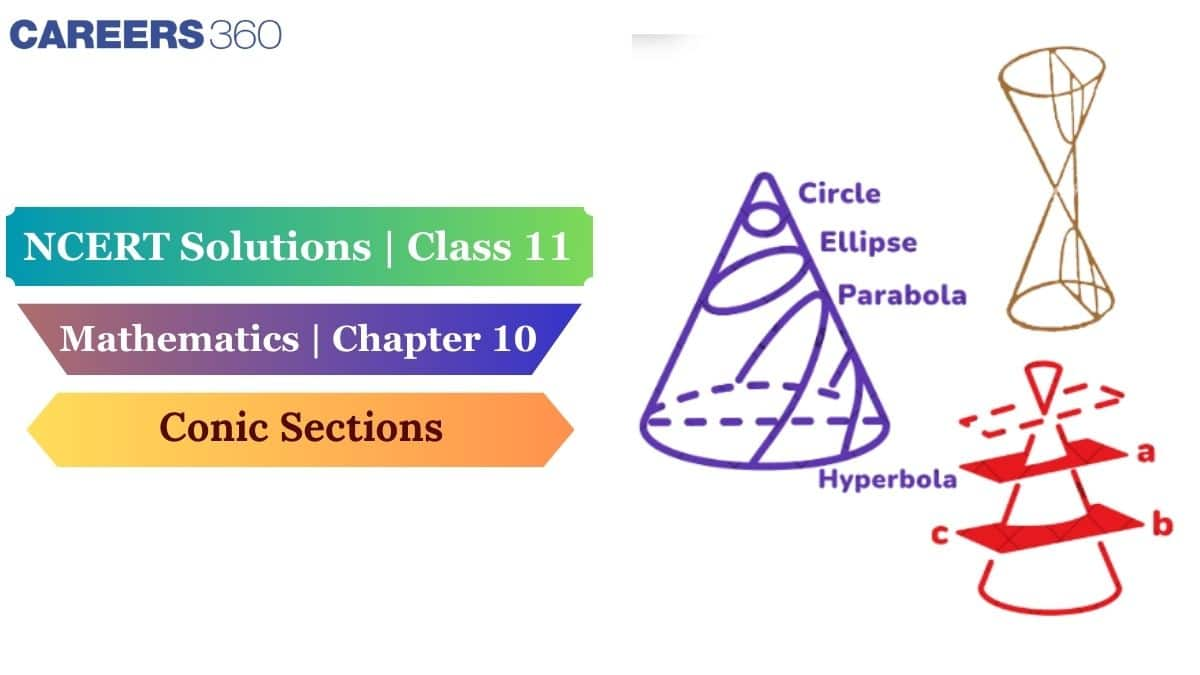
This article will explain all the Conic Sections class 11 questions and answers based on the latest NCERT 2025-26 syllabus in detail. Conic sections NCERT solutions are not only useful for CBSE board exams but also for competitive exams like JEE Mains, JEE Advanced, VITEEE, and BITSAT. Learnings from this chapter can be used in real-life applications like Wheels, satellite dishes, headlights, GPS, planetary orbits, MRI machines and many more. For a quick revision, students can use the PDFs of class 11 Maths chapter 10 NCERT solutions. Conic Section Class 11 Maths Chapter Notes and NCERT Exemplar Solutions For Class 11 Maths Chapter Conic Sections can also be used for mastering this chapter and deeper knowledge gain purposes.
| Circle | |
|
Description |
Equation/Formulae |
|
Equation of a circle |
(x - h)2 + (y - k)2 = r2 |
|
General equation of a circle |
x2 + y2 + 2gx + 2fy + c = 0 |
|
Centre of the circle |
Centre: (-g, -f) |
|
Radius of the circle |
Radius (r) = |
|
Parametric equation of a circle |
x = r cos(θ), y = r sin(θ) |
|
Parametric equation of a circle (centre at h, k) |
x = h + r cos(θ), y = k + r sin(θ) |
| Parabola | |
|
Description |
Equations/Forms |
|
Equation forms of parabola |
y2 = 4ax, y2 = -4ax, x2 = 4ay, x2 = -4ay |
|
Axis of the parabola |
y = 0 (for first two forms), x = 0 (for last two forms) |
|
Directrix of the parabola |
x = -a (1st form), x = a (2nd form), y = -a (3rd form), y = a (4th form) |
|
Vertex of the parabola |
(0, 0) (for all forms) |
|
Focus of the Parabola |
(a, 0) (1st form), (-a, 0) (2nd form), (0, a) (3rd form), (0, -a) (4th form) |
|
Length of the latus rectum |
4a (for all forms) |
|
Ellipse | |
|
Description |
Equation/Forms |
|
Equation forms of ellipse | And |
|
Major Axis |
y = 0 (1st form), x = 0 (2nd form) |
|
Length of Major Axis |
2a (for both forms) |
|
Minor Axis |
x = 0 (1st form), y = 0 (2nd form) |
|
Length of Minor Axis |
2b (for both forms) |
|
Directrix of the ellipse | x = |
|
Vertex of the ellipse |
(±a, 0) (1st form), (0, ±a) (2nd form) |
|
Focus of the ellipse |
(±ae, 0) (1st form), (0, ±ae) (2nd form) |
|
Length of the latus rectum | |
|
Eccentricity (e) |
|
| Hyperbola | |
|
Description |
Equations/Forms |
|
Equation forms of the hyperbola | And |
|
Coordinates of centre |
(0, 0) (for both forms) |
|
Coordinates of vertices |
(±a, 0) (for both forms) |
|
Coordinates of foci |
(±ae, 0) (for both forms) |
|
Length of Conjugate axis |
2b (for both forms) |
|
Length of Transverse axis |
2a (for both forms) |
|
Equation of Conjugate axis |
x = 0 (for both forms) |
|
Equation of Transverse axis |
y = 0 (for both forms) |
|
Equation of Directrix |
x = |
|
Eccentricity (e) |
|
|
Length of the latus rectum |
|
| NCERT Conic Sections Class 11 Solutions: Exercise: 11.1 Page Number: 181 Total Questions: 15 |
Question:1 Find the equation of the circle with centre (0,2) and radius 2.
Answer:
As we know, the equation of the circle with centre (h, k) and radius r is given by:
Here,
So the equation of the circle is:
Question:2 Find the equation of the circle with centre (–2,3) and radius 4.
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
Here
So the equation of the circle is:
Question:3 Find the equation of the circle with centre
Answer:
As we know, the equation of the circle with centre ( h, k) and radius r is given by:
Here,
So the equation of the circle is:
Question:4 Find the equation of the circle with centre (1,1) and radius
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
Here
So the equation of the circle is:
Question:5 Find the equation of the circle with centre
Answer:
As we know,
The equation of the circle with centre ( h, k) and radius r is given by:
Here
So the equation of the circle is:
Question:6 Find the centre and radius of the circles:
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
Here,
It can also be written in the form:
After comparing, we can see that,
Hence, the radius of the circle is 6.
Question:7 Find the centre and radius of the circles:
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
Here
It can also be written in the form:
After comparing, we can see that,
Hence, the radius of the circle is
Question:8 Find the centre and radius of the circles:
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
Here,
It can also be written in the form:
After comparing, we can see that
Hence, the radius of the circle is
Question:9 Find the centre and radius of the circles:
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
Here,
It can also be written in the form:
After comparing, we can see that,
Hence, centre of the circle is the
Question:10: Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
Condition 1: The circle passes through points (4,1) and (6,5).
Here,
Condition 2: Centre is on the line
So,
From condition 1 and condition 2, we get,
Substituting the values of h and k in condition 1, we get,
Question:11: Find the equation of the circle passing through the points (2,3) and (–1,1) and whose centre is on the line
Answer:
As we know,
The equation of the circle with centre ( h, k) and radius r is given by ;
Condition 1: The circle passes through points (2,3) and (–1,1).
Here,
Condition 2: The centre is on the line
So,
From condition 1 and condition 2, we get,
Substituting the values of h and k in condition 1, we get,
Question:12: Find the equation of the circle with radius 5, whose centre lies on the x-axis and passes through the point (2,3).
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
So let the circle be,
Since its radius is 5 and its centre lies on the x-axis,
And since it passes through the point (2,3).
When
When
Question:13: Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.
Answer:
Let the equation of circle be
Now, since this circle passes through (0, 0),
Now, this circle makes an intercept of a and b on the coordinate axes. it means the circle passes through the points (a, 0) and (0, b).
So,
Since
Similarly,
Since b is not equal to zero.
So the final equation of the Circle is:
Question:14: Find the equation of a circle with a centre (2,2) and passes through the point (4,5).
Answer:
Let the equation of the circle be:
Now, since the centre of the circle is (2,2), our equation becomes:
Now, since this passes through the point (4,5),
Hence, The Final equation of the circle becomes:
Question:15 Does the point (–2.5, 3.5) lie inside, outside or on the circle
Answer:
Given, a circle
As we can see, the center of the circle is (0, 0).
Now the distance(d) between (0,0) and (–2.5, 3.5) is:
Since the distance between the given point and the centre of the circle is less than the radius of the circle, the point lies inside the circle.
| NCERT Conic Sections Class 11 Solutions: Exercise: 11.2 Page Number: 186-187 Total Questions: 12 |
Answer:
Given a parabola with equation
This is a parabola of the form
So, by comparing the given parabola equation with the standard equation, we get,
Hence,
Coordinates of the focus :
Axis of the parabola:
It can be seen that the axis of this parabola is the X-axis.
The equation of the directrix:
The length of the latus rectum:
Answer:
Given a parabola with equation
This is a parabola of the form
So, by comparing the given parabola equation with the standard equation, we get,
Hence,
Coordinates of the focus :
Axis of the parabola:
It can be seen that the axis of this parabola is the Y-axis.
The equation of the directrix:
The length of the latus rectum:
Answer:
Given a parabola with equation
This is a parabola of the form
So, by comparing the given parabola equation with the standard equation, we get,
Hence,
Coordinates of the focus :
Axis of the parabola:
It can be seen that the axis of this parabola is the X-axis.
The equation of the directrix:
The length of the latus rectum:
Answer:
Given a parabola with equation
This is a parabola of the form
So, by comparing the given parabola equation with the standard equation, we get,
Hence,
Coordinates of the focus :
Axis of the parabola:
It can be seen that the axis of this parabola is the Y-axis.
The equation of the directrix
The length of the latus rectum:
Answer:
Given a parabola with equation
This is a parabola of the form
So, by comparing the given parabola equation with the standard equation, we get,
Hence,
Coordinates of the focus :
Axis of the parabola:
It can be seen that the axis of this parabola is the X-axis.
The equation of the directrix:
The length of the latus rectum:
Answer:
Given a parabola with an equation
This is a parabola of the form
So, by comparing the given parabola equation with the standard equation, we get,
Hence,
Coordinates of the focus :
Axis of the parabola:
It can be seen that the axis of this parabola is the Y-axis.
The equation of the directrix:
The length of the latus rectum:
Question:7 Find the equation of the parabola that satisfies the given conditions: Focus (6,0); directrix
Answer:
Given, in a parabola,
Focus : (6,0) And Directrix :
Here,
Focus is of the form (a, 0), which means it lies on the X-axis.
Directrix is of the form
These are the conditions when the standard equation of a parabola is.
Hence, the Equation of the Parabola is
Here, it can be seen that:
Hence, the Equation of the Parabola is:
Question:8 Find the equation of the parabola that satisfies the given conditions: Focus (0,–3); directrix
Answer:
Given, in a parabola,
Focus : Focus (0,–3); directrix
Here,
Focus is of the form (0, -a), which means it lies on the Y-axis.
Directrix is of the form
These are the conditions when the standard equation of a parabola is
Here, it can be seen that:
Hence, the Equation of the Parabola is:
Question:9 Find the equation of the parabola that satisfies the given conditions: Vertex (0,0); focus (3,0)
Answer:
Given,
Vertex (0,0) and focus (3,0)
As the vertex of the parabola is (0,0) and the focus lies on the positive X-axis, the parabola will open towards the right. The standard equation of such a parabola is
Here, it can be seen that
So, the equation of a parabola is
Question:10 Find the equation of the parabola that satisfies the given conditions: Vertex (0,0); focus (-2,0)
Answer:
Given: Vertex (0,0) and focus (-2,0)
As the vertex of the parabola is (0,0) and the focus lies in the negative X-axis, the parabola will open towards the left, and the standard equation of such a parabola is
Here, it can be seen that
So, the equation of a parabola is:
Question:11: Find the equation of the parabola that satisfies the given conditions: Vertex (0,0) passing through (2,3) and axis is along the x-axis.
Answer:
Given
The Vertex of the parabola is (0,0).
The parabola is passing through (2,3), and the axis is along the x-axis; it will open towards the right. and the standard equation of such a parabola is
Now, since it passes through (2,3)
So the Equation of the Parabola is:
Answer:
Given a parabola with Vertex (0,0), passing through (5,2) and symmetric with respect to the y-axis.
Since the parabola is symmetric with respect to the Y-axis, its axis will be the Y-axis. and since it passes through the point (5,2), it must go through the first quadrant.
So the standard equation of such a parabola is
Now, since this parabola is passing through (5,2)
Hence, the equation of the parabola is:
| NCERT Conic Sections Class 11 Solutions: Exercise: 11.3 Page Number: 195 Total Questions: 20 |
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
We get,
So,
Hence,
Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
We get,
So,
Hence,
Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
We get,
So,
Hence, the Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
We get,
So,
Hence, the Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of ellipse
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
We get,
So,
Hence, the Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
We get,
So,
Hence,
Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
We get,
So,
Hence, the Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
We get,
So,
Hence, the Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Answer:
The equation of the ellipse
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
We get,
So,
Hence, the Coordinates of the foci:
The vertices:
The length of the major axis:
The length of the minor axis:
The eccentricity :
The length of the latus rectum:
Question:10: Find the equation for the ellipse that satisfies the given conditions: Vertices (± 5, 0), foci (± 4, 0)
Answer:
Given, in an ellipse,
Vertices (± 5, 0), foci (± 4, 0)
Here Vertices and focus of the ellipse are on the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So, on comparing standard parameters( vertices and foci) with the given one, we get
Now, as we know the relation,
Hence, The Equation of the ellipse will be :
Question:11: Find the equation for the ellipse that satisfies the given conditions: Vertices (0, ± 13), foci (0, ± 5)
Answer:
Given, in an ellipse, Vertices (0, ± 13), foci (0, ± 5)
Here Vertices and focus of the ellipse are on the Y-axis, so the major axis of this ellipse will be the Y-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So, on comparing standard parameters( vertices and foci) with the given one, we get
Now, as we know the relation,
Hence, The Equation of the ellipse will be :
Question:12: Find the equation for the ellipse that satisfies the given conditions: Vertices (± 6, 0), foci (± 4, 0)
Answer:
Given, in an ellipse, Vertices (± 6, 0), foci (± 4, 0)
Here Vertices and focus of the ellipse are on the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So, on comparing standard parameters( vertices and foci) with the given one, we get
Now, as we know the relation,
Hence, The Equation of the ellipse will be :
Answer:
Given, in an ellipse,
Ends of the major axis (± 3, 0), ends of minor axis (0, ± 2)
Here, the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So, on comparing standard parameters( ends of the major and minor axis ) with the given one, we get
Hence, The Equation of the ellipse will be :
Answer:
Given, in an ellipse,
Ends of the major axis (0, ±
Here, the major axis of this ellipse will be the Y-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So on comparing standard parameters( ends of the major and minor axis ) with the given one, we get
Hence, The Equation of the ellipse will be :
Answer:
Given, in an ellipse,
Length of major axis 26, foci (± 5, 0)
Here, the focus of the ellipse is on the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So on comparing standard parameters( Length of semimajor axis and foci) with the given one, we get
Now, as we know the relation,
Hence, The Equation of the ellipse will be :
Question:16: Find the equation for the ellipse that satisfies the given conditions: Length of minor axis 16, foci (0, ± 6).
Answer:
Given, in an ellipse,
Length of minor axis 16, foci (0, ± 6).
Here, the focus of the ellipse is on the Y-axis, so the major axis of this ellipse will be the Y-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So, on comparing standard parameters( length of semi-minor axis and foci) with the given one, we get
and
Now, as we know the relation,
Hence, The Equation of the ellipse will be :
Question:17 Find the equation for the ellipse that satisfies the given conditions: Foci (± 3, 0), a = 4
Answer:
Given, in an ellipse, V Foci (± 3, 0), a = 4
Here, foci of the ellipse is in the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
Where
So, on comparing standard parameters( vertices and foci) with the given one, we get
Now, as we know the relation,
Hence, The Equation of the ellipse will be :
Question:18 : Find the equation for the ellipse that satisfies the given conditions: b = 3, c = 4, centre at the origin; foci on the x-axis.
Answer:
Given: In an ellipse, b = 3, c = 4, centre at the origin; foci on the x-axis.
Here, foci of the ellipse is in the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
Where
Also Given,
Now, as we know the relation,
Hence, The Equation of the ellipse will be :
Answer:
Given, in an ellipse
Centre at (0,0), major axis on the y-axis and passes through the points (3, 2) and (1,6).
Since the major axis of this ellipse is on the Y-axis, the equation of the ellipse will be of the form:
Where
Now, since the ellipse passes through points (3, 2)
Since the ellipse also passes through points (1, 6).
On solving these two equations, we get,
Thus, the equation of the ellipse will be
Answer:
Given, in an ellipse
Major axis is on the x-axis and passes through the points (4,3) and (6,2).
Since the major axis of this ellipse is on the X-axis, the equation of the ellipse will be of the form:
Where
Now, since the ellipse passes through the point (4,3)
Since the ellipse also passes through the point (6, 2).
On solving these two equations, we get,
Thus, the equation of the ellipse will be
| NCERT Conic Sections Class 11 Solutions: Exercise: 11.4 Page Number: 202 Total Questions: 15 |
Answer:
Given a Hyperbola equation,
It can also be written as
Comparing this equation with the standard equation of the hyperbola, we get,
We get,
Now, as we know the relation in a hyperbola,
Here, as we can see from the equation, the axis of the hyperbola is the X-axis.
So, the Coordinates of the foci are:
The Coordinates of vertices:
The Eccentricity:
The Length of the latus rectum :
Question:2: Find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas:
Answer:
Given a Hyperbola equation,
It can also be written as
Comparing this equation with the standard equation of the hyperbola:
We get,
Now, as we know the relation in a hyperbola,
Here, as we can see from the equation, the axis of the hyperbola is the Y-axis.
So, the Coordinates of the foci are:
The Coordinates of vertices:
The Eccentricity:
The Length of the latus rectum :
Answer:
Given a Hyperbola equation,
It can also be written as
Comparing this equation with the standard equation of the hyperbola:
We get,
Now, as we know the relation in a hyperbola,
Hence, the Coordinates of the foci:
The Coordinates of vertices:
The Eccentricity:
The Length of the latus rectum :
Answer:
Given a Hyperbola equation,
It can also be written as:
Comparing this equation with the standard equation of the hyperbola:
We get,
Now, as we know the relation in a hyperbola,
Therefore, the Coordinates of the foci are:
The Coordinates of vertices:
The Eccentricity:
The Length of the latus rectum :
Answer:
Given a Hyperbola equation,
It can also be written as:
Comparing this equation with the standard equation of the hyperbola:
We get,
Now, as we know the relation in a hyperbola,
Here, as we can see from the equation, the axis of the hyperbola is the Y-axis.
So, the Coordinates of the foci are:
The Coordinates of vertices:
The Eccentricity:
The Length of the latus rectum :
Answer:
Given a Hyperbola equation,
It can also be written as:
Comparing this equation with the standard equation of the hyperbola:
We get,
Now, as we know the relation in a hyperbola,
Therefore,
Coordinates of the foci:
The Coordinates of vertices:
The Eccentricity:
The Length of the latus rectum :
Answer:
Given, in a hyperbola: Vertices (± 2, 0), foci (± 3, 0)
Here, Vertices and foci are on the X-axis, so the standard equation of the Hyperbola will be ;
By comparing the standard parameter (Vertices and foci) with the given one, we get
Now, as we know, the relation in a hyperbola
Hence,The Equation of the hyperbola is
Answer:
Given, in a hyperbola: Vertices (0, ± 5), foci (0, ± 8)
Here, Vertices and foci are on the Y-axis, so the standard equation of the Hyperbola will be:
By comparing the standard parameter (Vertices and foci) with the given one, we get
Now, as we know, the relation in a hyperbola
Hence, The Equation of the hyperbola is:
Answer:
Given, in a hyperbola Vertices (0, ± 3), foci (0, ± 5)
Here, Vertices and foci are on the Y-axis, so the standard equation of the Hyperbola will be:
By comparing the standard parameter (Vertices and foci) with the given one, we get
Now, as we know, the relation in a hyperbola
Hence, The Equation of the hyperbola is
Answer:
Given, in a hyperbola: Foci (± 5, 0), the transverse axis is of length 8.
Here, the foci are on the X-axis, so the standard equation of the Hyperbola will be:
By comparing the standard parameter (transverse axis length and foci) with the given one, we get
Now, as we know, the relation in a hyperbola
Hence, The Equation of the hyperbola is
Answer:
Given, in a hyperbola: Foci (0, ±13), the conjugate axis is of length 24.
Here, the foci are on the Y-axis, so the standard equation of the Hyperbola will be:
By comparing the standard parameter (length of conjugate axis and foci) with the given one, we get
Now, as we know, the relation in a hyperbola
Hence, The Equation of the hyperbola is
Question:12: Find the equations of the hyperbola satisfying the given conditions: Foci
Answer:
Given, in a hyperbola: Foci
Here, foci are on the X-axis, so the standard equation of the Hyperbola will be ;
By comparing the standard parameter (length of latus rectum and foci) with the given one, we get
Now, as we know, the relation in a hyperbola
Since
So,
Hence, The Equation of the hyperbola is
Answer:
Given, in a hyperbola: Foci (± 4, 0), the latus rectum is of length 12
Here, foci are on the X-axis, so the standard equation of the Hyperbola will be:
By comparing the standard parameter (length of latus rectum and foci) with the given one, we get
Now, as we know, the relation in a hyperbola
Since
So,
Hence, The Equation of the hyperbola is
Question:14: Find the equations of the hyperbola satisfying the given conditions: vertices (± 7,0),
Answer:
Given, in a hyperbola: vertices (± 7,0), and
Here, Vertices is on the X-axis, so the standard equation of the Hyperbola will be:
By comparing the standard parameter (Vertices and eccentricity) with the given one, we get,
Now, as we know, the relation in a hyperbola
Hence, The Equation of the hyperbola is
Question:15 Find the equations of the hyperbola satisfying the given conditions: Foci
Answer:
Given, in a hyperbola: Foci
Since the foci of the hyperbola is on the Y-axis, the equation of the hyperbola will be of the form:
By comparing the standard parameter (foci) with the given one, we get
Now, as we know, in a hyperbola
Now, as the hyperbola passes through the point (2,3),
Solving Equations (1) and (2), we get,
Now, as we know in a hyperbola
we choose the value
So,
Hence The Equation of the hyperbola is
| NCERT Conic Sections Class 11 Solutions: Exercise: Miscellaneous Exercise Page Number: 204 Total Questions: 8 |
Question:1: If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.
Answer:
Let the parabolic reflector open towards the right.
So, the equation of the parabolic reflector will be
Now, since this curve will pass through the point (5,10), if we assume origin at the optical centre,
So,
Hence, the focus of the parabola is
Alternative Method:
As we know, on any concave curve, focus,
Hence, the focus is 5 cm right to the optical centre.
Answer:
Since the Axis of the parabola is vertical, let the equation of the parabola be
it can be seen that this curve will pass through the point (
So,
Hence, the equation of the parabola is:
Now, when y = 2 the value of x will be:
Hence, the width of the arch at this height is:
Answer:
Given,
The width of the parabolic cable = 100m
The length of the shorter supportive wire attached = 6m
The length of the longer supportive wire attached = 30m
Since the rope opens upwards, the equation will be of the form
Now, if we consider the origin at the centre of the rope, the equation of the curve will pass through points: (50, 30-6) = (50,24)
Hence, the equation of the parabola is
Now, at a point 18 m right from the centre of the rope, the x coordinate of that point will be 18.
So, by the equation, the y-coordinate will be:
Hence, the length of the supporting wire attached to the roadway from the middle is
(3.11 + 6)m = 9.11 m
Answer:
The equation of the semi-ellipse will be of the form
Now, according to the question,
the length of major axis = 2a = 8
The length of the semi-major axis = 2
Hence, the equation will be,
Now, at point 1.5 cm from the end, the x coordinate is
So, the height at this point is
Hence, the height of the required point is 1.56 m.
Answer:
Let
Now, at a point 3 cm from the end,
At the point of touching the ground
Now, as we know the trigonometric identity,
Hence, the equation is
Answer:
Given the parabola,
Comparing this equation with
Now, as we know, the coordinates of the ends of the latus rectum are:
So, the coordinates of the latus rectum are,
Now the area of the triangle with coordinates (0,0),(6,3) and (-6,3)
Width of the triangle
Height of the triangle = 3
So, the area of the triangle
=
=
=
Hence, the required area is 18 square units.
Answer:
As we know, if a point moves in a plane in such a way that its distance from two points remains constant, then the path is an ellipse.
Now, according to the question,
The distance between the point from where the sum of the distance from a point is constant = 10
Now, the distance between the foci = 8
Now, as we know the relation,
Hence, the equation of the ellipse is:
Hence, the path of the man will be:
Answer:
Given an equilateral triangle inscribed in a parabola with the equation
The one coordinate of the triangle is A(0,0).
Now, let the other two coordinates of the triangle are
Now, since the triangle is equilateral,
The coordinates of the points of the equilateral triangle are,
So, the side of the triangle is:
Here, students can check the solved examples before moving on to the exercises. Exercises are also prepared based on difficulty levels varying from easy to moderate level. These links are separate links to the exercises. Students can check each exercise separately and try to solve the next one on their own before checking the solutions.
Class 11 maths chapter 10 question answers are essential for many things. But before solving them, strengthen your fundamentals of conic sections. Some important aspects of solving these problems are listed below.
All in all, mastering this chapter is an absolute necessity for students in class 11.
Students can use the following links to check the solutions of the other subjects to achieve good marks in the exam.
After studying the NCERT books for fundamental knowledge, students can solve problems from other books. Also, they can check the latest NCERT syllabus to stay updated using the following links.
Conic sections chapter in class 11 Covers the following topics:
There are also many important sub-topics like latus rectum, standard equations of the conic sections, foci, major/minor axis, directrix, and eccentricity.
Before solving the conic sections problems, familiarise yourself with all the basics, general equations, key properties, and important formulae of this chapter. Then follow the following steps.
You can find the free NCERT solutions on NCERT's official websites.
You can also check these detailed free solutions prepared by experienced careers360 experts explaining every detail and providing extra information about the exercises. Check the following links.
Here are some real-life uses of different conic sections.
| Circle | It can be used in clocks, wheels, planetary motions, CDs & DVDs, etc. |
| Parabola | It can be used in Satellite dishes, radio telescopes, Car headlights & flashlights, Projectile motions, Suspension bridges, etc. |
| Ellipse | It can be used in planetary orbits, MRI, Whispering galleries, Car & train tracks, etc. |
| Hyperbola | It can be used in navigation, GPS systems, Nuclear radiation detection, optical lenses, cooling towers, boomerangs, telescopes, etc. |
| Features | Ellipse | Parabola | Hyperbola |
| Definition | A set of points where the sum of the distances from two fixed foci is constant. | A set of points equidistant from a fixed point called the focus and a fixed line called the directrix. | A set of points where the absolute difference of distances from two fixed foci is constant. |
| Shape | Oval shaped | U-shaped | Two separate open curves(Look like two infinite bows) |
| Standard Equation | |||
| Foci | |||
| Eccentricity (e) |
Admit Card Date:06 May,2025 - 20 May,2025
Admit Card Date:06 May,2025 - 20 May,2025

Register for ALLEN Scholarship Test & get up to 90% Scholarship

Get up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes

This ebook serves as a valuable study guide for NEET 2025 exam.

This e-book offers NEET PYQ and serves as an indispensable NEET study material.

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters