NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry

Edited By Sumit Saini | Updated on Aug 18, 2022 02:28 PM IST

NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry - Chapter 1 is one of the important chapters of NCERT syllabus for Class 11 Chemistry and consists of important concepts that are often asked in Class 11 final examination. In this chapter, there are 36 questions in the NCERT book exercise. The NCERT solutions for Class 11 Chemistry chapter 1 Some Basic Concepts of Chemistry are designed systematically by the Chemistry subject experts. These NCERT solutions will help students in their preparation of class 6 to 12 final examination and also helps in competitive exams like JEE, NEET, BITSAT, etc. By referring to the NCERT solutions for Class 11 , students can understand all the important concepts and practice questions well enough before their examination
Some Basic Concepts of Chemistry Formulas
1. The mass percent of an element
$\\Mass\:percent\:of =\frac{Mass \:of\:that\:element\:in \:the\:compound\times 100}{molar \:mass\:of\:the\:compound}\\an\:element$
2. Mass percent
$\\Mass\:percent =\frac{Mass \:of\:solute\times 100}{mass\:of\:solution}\\$
3. Mole fraction
$\\Mole\: fraction \:of \:A =\frac{No. \:of\:moles\:of\:A}{No.\:of\:moles\:of\:solutions}=\frac{n_A}{n_A+n_B}$
4. Molarity(M)
$\\M =\frac{No. \:of\:moles\:of\:solute}{Volume\:of\:solution\:in\:litres}$
5. Molality(m)
$\\m =\frac{No. \:of\:moles\:of\:solute}{Mass\:of\:solvent\:in\:Kg}$

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

NEET Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | ALLEN

Scholarship Test: Vidyamandir Intellect Quest (VIQ)

NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry - Exercise Questions

Question 1.1 Calculate the molar mass of the following:
(i) H ₂ O

Answer :

The molar mass of Water $(H_{2}O)$ is:

$= 2\times Atomic\ mass\ of\ hydrogen\ + \ Atomic\ mass\ of\ oxygen$

$= 2\times(1.008\ u) + 16.00\ u$

$= 18.02\ u$

Question 1.1 Calculate the molar mass of the following:
(ii) CO ₂

Answer :

The molar mass of Carbon dioxide $CO_{2}$ is:

$= 1\times Atomic\ mass\ of\ carbon\ + \ 2\times Atomic\ mass\ of\ oxygen$

$= 1\times(12.011\ u) + 2\times (16.00\ u)$

$= 44.011\ u$

Question 1.1 Calculate the molar mass of the following:
(iii) CH 4

Answer :

The molar mass of Methane $CH_{4}$ is:

$= 1\times Atomic\ mass\ of\ carbon\ + \ 4\times Atomic\ mass\ of\ hydrogen$

$= 1\times(12.011\ u) + 4\times (1.008\ u)$

$= 16.043\ u$

Question 1.2 Calculate the mass per cent of different elements present in sodium sulphate (Na ₂ SO ₄ ).

Answer :

The different elements present in sodium sulphate are:

Sodium (Na), Sulphur (S), and Oxygen (O).

The molar mass of sodium sulphate $Na_{2}SO_{4}$ ; $= (2\times Atomic\ mass\ of\ Na) + (1\times Atomic\ mass\ of\ S) + (4\times Atomic\ mass\ of\ O)$

$= 2\times (23.0\ u) + (32.066\ u) + 4\times (16.00\ u)$

$= 142.066\ u$

So, the mass percentage of an element in a compound is given by,

$= \frac{Mass\ of\ element\ in\ the\ compound}{Molar\ mass\ of\ the\ compound} \times 100$

Therefore,

The mass per cent of Sodium (Na):

$=\frac{46.0\ u}{142.066\ u} \times 100$

$=32.379\%$

$\approx 32.4\%$

The mass per cent of Sulphur (S):

$=\frac{32.066\ u}{142.066\ u} \times 100$

$= 22.57 \%$

$\approx 22.6\%$

The mass per cent of Oxygen (O):

$=\frac{64.0\ u}{142.066\ u} \times 100$

$= 45.049 \%$

$\approx 45.0\%$

Question 1.3 Determine the empirical formula of an oxide of iron, which has 69.9% iron and 30.1% dioxygen by mass.

Answer :

Given there is an oxide of iron which has $69.9\%$ iron and $30.1\%$ dioxygen by mass:

Relative moles of iron in iron oxide:

$= \frac{\%\ of\ iron\ by\ mass}{Atomic\ mass\ of\ iron}$

$= \frac{69.9}{55.85} = 1.25$

Relative moles of oxygen in iron oxide:

$= \frac{\%\ of\ oxygen\ by\ mass}{Atomic\ mass\ of\ oxygen}$

$= \frac{30.1}{16.00} = 1.88$

The simplest molar ratio of iron to oxygen:

$\Rightarrow 1.25:1.88$ $\Rightarrow 1:1.5$ $\Rightarrow 2:3$

Therefore, the empirical formula of the iron oxide is $Fe_{2}O_{3}$ .

Question 1.4 Calculate the amount of carbon dioxide that could be produced when

(i) 1 mole of carbon is burnt in the air.

Answer :

When carbon is burnt in the air:

The chemical equation for this reaction is:

$C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}$

Here 1 mole of carbon (solid) weighing 12g is burnt in 1 mole of Dioxygen (gas) weighing 32g to produce 1 mole of carbon dioxide (gas) weighing 44g.

Question 1.4 Calculate the amount of carbon dioxide that could be produced when

(ii) 1 mole of carbon is burnt in 16 g of dioxygen.

Answer :

When carbon is burnt in 16 g of dioxygen:

The chemical equation for this reaction is:

$C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}$

Here, oxygen acts as a limiting reagent as only 16g of dioxygen is available.

Hence, it will react with 0.5 mole of carbon to give 22g of carbon dioxide.

Question 1.4 Calculate the amount of carbon dioxide that could be produced when

(iii) 2 moles of carbon are burnt in 16 g of dioxygen.

Answer :

When 2 moles of carbon is burnt in 16 g of dioxygen:

The chemical equation for this reaction is:

$C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}$

Here, oxygen acts as a limiting reagent as only 16g of dioxygen is available.

Thus, 16g of dioxygen will react with 0.5 mole of carbon to give 22g of carbon dioxide.

Question 1.5 Calculate the mass of sodium acetate (CH ₃ COONa) required to make 500 mL of 0.375 molar aqueous solution. Molar mass of sodium acetate is 82.0245 g mol ^–1 .

Answer :

$0.375$ molar aqueous solution would contain $0.375$ moles of $CH_{3}COONa$ dissolved in $1000mL$ of solvent.

So, we have to calculate for $500mL$ solution of $CH_{3}COONa$ .

Therefore the number of moles of sodium acetate in $500mL$ will be:

$= \frac{0.375}{1000}\times 500$

$=0.1875\ mole$

Given Molar mass of sodium acetate: $82.0245\ g\ mol^{-1}$

So, the required mass of sodium acetate $= (82.0245\ g\ mol^{-1})\times (0.1875\ mole)$

$= 15.38\ grams$

Question 1.6 Calculate the concentration of nitric acid in moles per litre in a sample which has a density, 1.41 g mL ^- ¹ and the mass percent of nitric acid in it being 69%.

Answer :

Given the mass percentage of nitric acid is $69\%$ .

That means 69 grams of nitric acid are present in 100 grams of nitric acid solution.

The molar mass of nitric acid $HNO_{3}$ is $1+14+ 3\times (16) = 63g\ mol^{-1}$ .

So, the number of moles in 69g of Nitric acid:

$= \frac{69}{63}\ moles = 1.095\ moles$

and volume of 100g of the nitric acid solution:

$=\frac{100}{1.41}mL = 70.92mL = 0.07092\ L$

Therefore, the concentration of Nitric acid in moles per litre is:

$= \frac{1.095}{0.07092} = 15.44\ M$

Question 1.7 How much copper can be obtained from 100 g of copper sulphate (CuSO ₄ )?

Answer :

Given that 100g of Copper sulphate $CuSO_{4}$ ;

1 mole of $CuSO_{4}$ contains 1 mole of copper.

Molar Mass of Copper sulphate is:

$= 63.5 + 32.00 + 4\times 16.00 = 159.5g$

Now, $159.5g$ of copper sulphate contains $63.5g$ of copper.

So, $100g$ of copper sulphate will contain copper content:

$=\frac{63.5}{159.5}\times 100 = 39.81g$

Question 1.8 Determine the molecular formula of an oxide of iron, in which the mass percent of iron and oxygen are 69.9 and 30.1, respectively. Given that the molar mass of the oxide is $159.69 g\ mol^{-1}$ .

Answer :

Given that the mass percentage of iron is $69.9\%$ and the mass percentage of oxygen is $30.1\%$

The atomic mass of iron $= 55.85\ u$ .

The atomic mass of oxygen $=16.00\ u$ .

So, the relative moles of iron in iron oxide will be:

$=\frac{mass\ of\ iron\ by\ mass}{Atomic\ mass\ of\ iron}$

$= \frac{69.9}{55.85} = 1.25$

And relative moles of oxygen in iron oxide will be:

$=\frac{mass\ of\ oxygen \ by\ mass}{Atomic\ mass\ of\ oxygen}$

$= \frac{30.01}{16.00} = 1.88$

Hence the simplest molar ratio:

$=\frac{1.25}{1.88}$ or $\Rightarrow 1:1.5 = 2:3$

Therefore, the empirical formula of iron oxide will be $Fe_{2}O_{3}$ .

Now, calculating the molar mass of $Fe_{2}O_{3}$ :

$=(2\times 55.85) + (3\times16.00) = 159.7g\ mol^{-1}$ .

Hence it is matching with the given molar mass of the oxide.

Question 1.9 Calculate the atomic mass (average) of chlorine using the following data:

% Natural Abundance Molar Mass
³⁵ Cl 75.77 34.9689
³⁷ Cl 24.23 36.9659

Answer :

To calculate the average atomic mass of chlorine:

Given the fractional natural abundance of $_{}^{35}\textrm{Cl}$ with $34.9689\ u$ molar mass is $75.77\%$ and that of $_{}^{37}\textrm{Cl}$ with $36.9659\ u$ molar mass is $24.23\%$ .

Therefore we have,

Average Atomic mass of Chlorine:

$= \left ( 0.7577\times34.9689\ u \right ) + \left ( 0.2423\times36.9659\ u \right )$

$= 26.4959\ u + 8.9568\ u = 35.4527\ u$

Question 1.10 In three moles of ethane (C ₂ H ₆ ), calculate the following:

(i) Number of moles of carbon atoms.

Answer :

Given there are three moles of Ethane $C_{2}H_{6}$ ;

So, 1 mole of $C_{2}H_{6}$ contains 2 moles of carbon atoms.

Therefore, 3 moles of $C_{2}H_{6}$ contains 6 moles of carbon atoms.

Question 1.10 In three moles of ethane (C ₂ H ₆ ), calculate the following:

(ii) Number of moles of hydrogen atoms.

Answer :

Given there are three moles of Ethane $C_{2}H_{6}$ ;

So, 1 mole of $C_{2}H_{6}$ contains 6 moles of hydrogen atoms.

Therefore, 3 moles of $C_{2}H_{6}$ contains 18 moles of hydrogen atoms.

Question 1.10 In three moles of ethane (C ₂ H ₆ ), calculate the following:

(iii) Number of molecules of ethane.

Answer :

Given there are three moles of Ethane $C_{2}H_{6}$ ;

So, 1 mole of $C_{2}H_{6}$ contains $6.02\times 10^{23}$ molecules of ethane.

Therefore, 3 moles of $C_{2}H_{6}$ contains $3\times6.02\times 10^{23} = 18.06\times10^{23}$ molecules of ethane.

Question 1.11 What is the concentration of sugar (C ₁₂ H ₂₂ O ₁₁ ) in mol L ^–1 if its 20 g are dissolved in enough water to make a final volume up to 2L?

Answer :

The molar mass of sugar $C_{12}H_{22}O_{11}$ is:

$= (12\times12)+ (1\times 22)+(11\times16) = 342g\ mol^{-1}$ .

The number of moles of sugar in 20g of sugar will be:

$= \frac{20}{342} = 0.0585\ mole$

and given the volume of the solution after dissolving enough water is 2L .

$Molar\ concentration = \frac{Moles\ of\ solute}{Volume\ of\ solution\ in\ 1L}$

$= \frac{0.0585mol}{2L} = 0.0293mol\ L^{-1} = 0.0293\ M$

Question 1.12 If the density of methanol is 0.793 kg L ^–1 , what is its volume needed for making 2.5 L of its 0.25 M solution?

Answer :

Given that the density of methanol $CH_{3}OH$ is $0.793 Kg\ L^{-1}$ .

So, the number of moles present in the methanol per litre will be or the Molarity of the solution will be :

$= \frac{0.793Kg\ L^{-1}}{0.032Kg\ mol^{-1}} = 24.78\ mol\ L^{-1}$

Now, to make 2.5L of its 0.25M solution:

We will apply the formula: $M_{1}V_{1} (for\ given\ solution) = M_{2}V_{2} (for\ solution\ to\ be\ prepared)$

$24.78\times V_{1} =0.25\times 2.5L$

$V_{1} = 0.02522L\ or\ 25.22\ mL$ .

Hence $25.22\ mL$ volume will be required for making 2.5L of methanol 0.25M solution.

Question 1.13 Pressure is determined as force per unit area of the surface. The SI unit of pressure, pascal is as shown below:
1 Pa = 1 Nm ^–2
If mass of air at sea level is 1034 g cm ^–2 , calculate the pressure in pascal.

Answer :

The pressure is as given is force per unit area of the surface.

$Pressure = \frac{Force}{Area}$

Given to calculate the pressure exerted by the air on sea water, if the mass of air at sea level is $1034\ g\ cm^{-2}$ .

The force with which the air is exerting on the surface is:

$= \frac{1034g\times9.8ms^{-2}}{cm^2}\times\frac{1kg}{1000g}\times\frac{100cm}{1m} = 1.01332\times10^5\ N$

Now,

as $1 Pascal = 1N\ m^{-2}$

Therefore, $1.01332\times10^5N\timesm^{-2} = 1.01332\times10^{5}\ Pa$

Question 1.14 What is the SI unit of mass? How is it defined?

Answer :

The SI unit of mass is Kilogram (Kg).

It is defined as the mass of platinum-iridium (Pt-Ir) cylinder that is stored in an air-tight jar at the International Bureau of Weigh and Measures in France.

Question 1.15 Match the following prefixes with their multiples:

Prefixes Multiples

(i) micro 10 ⁶
(ii) deca 10 ⁹
(iii) mega 10 ^–6
(iv) giga 10 ^–15
(v) femto 10

Answer :

Matched items are given in below table:

Prefixes	Multiples
(i) micro	$10^{-6}$
(ii) Deca	$10$
(iii) Mega	$10^6$
(iv) Giga	$10^9$
(v) femto	$10^{-15}$

Question 1.16 What do you mean by significant figures?

Answer :

Significant figures are meaningful digits that are known with certainty including the last digit whose value is uncertain.

For example: if we write a result as 56.923 Kg, we say the 56.92 is certain and 3 is uncertain and the uncertainty would be $\pm 1$ in the last digit. Here we also include the last uncertain digit in the significant figures.

Question 1.17 A sample of drinking water was found to be severely contaminated with chloroform, CHCl ₃ , supposed to be carcinogenic in nature. The level of contamination was 15 ppm (by mass).

(i) Express this in per cent by mass.

Answer :

1ppm means 1 parts in million $(10^6)$ parts.

So, in percentage by mass:

We have,

$Percentage\ by\ mass = \frac{15}{10^6}\times 100 = 15\times10^{-4}$

$= 1.5\times10^{-3}\%$

(ii) Determine the molality of chloroform in the water sample .

Answer :

The molarity of chloroform sample in water will be:

$= \frac{number\ of\ moles\ present}{Volume\ of\ solution\ in\ L}$

The molar mass of Chloroform $CHCl_{3}$ :

$= 12+1+(3\times35.5) = 118.5g\ mol^{-1}$

So we have calculated in the previous part that percentage by mass of chloroform is $1.5\times10^{-3}$ .

Hence in 100g sample, there will be $1.5\times10^{-3}g$ of chloroform.

Therefore, 1000g (1Kg) of the sample will contain choroform $= 1.5\times10^{-2}g$ .

$= \frac{1.5\times10^{-2}}{118.65\ mol} = 1.266\times 10^{-4}\ mol$

Therefore, the molarity of chloroform in the water sample is $1.266\times 10^{-4}\ M$ .

Question 1.18 Express the following in the scientific notation:

(i) 0.0048

Answer :

The scientific notation of $0.0048$ will be $4.8\times 10^{-3}$ .

Question 1.18 Express the following in the scientific notation:

(ii) 234,000

Answer :

The scientific notation of $234,000$ will be $2.34\times10^5$ .

Question 1.18 Express the following in the scientific notation:

(iii) 8008

Answer :

The scientific notation of $8008$ will be $8.008\times 10^3$ .

Question 1.18 Express the following in the scientific notation:

(iv) 500.0

Answer :

The scientific notation of $500.0$ will be $5.000\times10^2$ .

Question 1.18 Express the following in the scientific notation:

(v) 6.0012

Answer :

The scientific notation of $6.0012$ will be $6.0012\times10^0$

Question 1.19 How many significant figures are present in the following?

(i) 0.0025

Answer :

There are 2 significant digits because all non-zero digits are in a number are significant and the zeros written to the left of the first non-zero digit in a number are non-significant.

Question 1.19 How many significant figures are present in the following?

(ii) 208

Answer :

There are 3 significant digits because all non-zero digits are in a number are significant and the zeros between two non-zero digits are always significant.

Question 1.19 How many significant figures are present in the following?

(iii) 5005

Answer :

There are 4 significant digits because all non-zero digits are in a number are significant and the zeros between two non-zero digits are always significant.

Question 1.19 How many significant figures are present in the following?

(iv) 126,000

Answer :

There are 3 significant digits because all non-zero digits are in a number are significant and the terminal zeros are not significant if there is no decimal point.

Question 1.19 How many significant figures are present in the following?

(v) 500.0

Answer :

There are 4 significant digits because the zeros written to the left of the first non-zero digit in a number are non-significant and all zeros placed to the right of a decimal point in a number are significant.

Question 1.19 How many significant figures are present in the following?

(vi) 2.0034

Answer :

There are 5 significant digits because all zeros placed to the right of a decimal point in a number are significant.

Question 1.20 Round up the following upto three significant figures:

(i) 34.216

Answer :

After round upto three significant figures:

Answer - $34.2$

Question 1.20 Round up the following upto three significant figures:

(ii) 10.4107

Answer :

After round upto three significant figures:

Answer - $10.4$ .

Question 1.20 Round up the following upto three significant figures:

(iii) 0.04597

Answer :

After round up to three significant figures:

Here the rightmost digit to be removed is more than 5 i.e., 7, then the preceding number is increased by one. So we get $0.0460$ .

Answer - $0.0460$

Question 1.20 Round up the following upto three significant figures:

(iv) 2808

Answer :

After round upto three significant figures:

Here the rightmost digit to be removed is more than 5 i.e., 8, then the preceding number is increased by one. So we get $2810$ .

Answer - $2810$

Question 1.21 The following data are obtained when dinitrogen and dioxygen react together to form different compounds:
Mass of dinitrogen Mass of dioxygen
(i) 14 g 16 g
(ii) 14 g 32 g
(iii) 28 g 32 g
(iv) 28 g 80 g
(a) Which law of chemical combination is obeyed by the above experimental data? Give its statement.

Answer :

Here if we fix the mass of dinitrogen at 14g, then the masses of dioxygen that will combine with the fixed mass of dinitrogen are 16g, 32g, 32g, and 80g.

The masses of dioxygen bear a whole number ratio of 1:2:2:5.

Hence, the given experimental data obeys the Law of Multiple Proportionals .

The law given by Dalton states that "if two elements can combine to form more than one compound, the masses of one element that combine with a fixed mass of the other element, are in the ratio of small whole numbers".

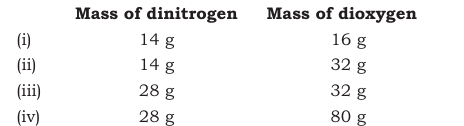
(b) Fill in the blanks in the following conversions:
(i) 1 km = ...................... mm = ...................... pm
(ii) 1 mg = ...................... kg = ...................... ng
(iii) 1 mL = ...................... L = ...................... dm ³

Answer :

(i) As we know in $1km = 1000m$ or $1m = 1000mm$ . or $1 km = 1000\times1000 mm =10^6 mm$

And $1pm = 1\times10^{-12}m$ or $1km = 10^{15} pm$

Therefore we have,

$1 km = 10^6 mm =10^{15} pm$

(ii) As we know in $1kg = 1000g$ or $1g = 1000mg$ . or $1 kg = 1000\times1000 mg$ or $1mg = \frac{1}{10^6} kg=10^{-6}kg$

And $1 ng = 10^{-9}g$ or $1ng = 10^{-9}\times1000mg$ or $1ng = 10^{-6}mg$

or $1 mg =10^6ng$ .

Therefore we have,

$1 mg = 10^{-6} kg =10^{6} ng$ .

(iii) As we know in $1L= 1000mL$ or $1mL =\frac{1}{1000}L = 10^{-3}L$

or $1dm = 0.1 m \Rightarrow 1dm = 10cm$ or $1cm = 0.1dm$

And 1mL = 1cm^3 or we can write it as: $1mL = \frac{1dm}{10cm}\times\frac{1dm}{10cm}\times\frac{1dm}{10cm}$

And $1mL = 10^{-3}dm^3$

Therefore we have,

$1mL = 10^{-3}L =10^{-3}dm^3$

Question 1.22 If the speed of light is $3.0 \times 10^8 m s^{-1}$ , calculate the distance covered by light in 2.00 ns.

Answer :

Given the speed of light to be $3.0 \times 10^8 m s^{-1}$ , so the distance covered by light in 2.00 ns. will be:

$Distance = Speed\times Time$

$Distance = (3.0\times10^{8}ms^{-1})\times(2.00\times10^{-9}sec) = 6.00\times10^{-1}m = 0.600m$

Therefore, the light will travel 0.600 metres in 2 nano seconds.

Question 1.23 In a reaction
$A + B_2 \rightarrow AB_2$
Identify the limiting reagent, if any, in the following reaction mixtures.