Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 13.9 Class 9 Maths Chapter 13 - Surface Area and Volumes

NCERT Solutions for Exercise 13.9 Class 9 Maths Chapter 13 - Surface Area and Volumes

Edited By Sumit Saini | Updated on Jul 06, 2022 02:31 PM IST

NCERT Solutions for Class 9 Maths exercise 13.9 is an optional last exercise which covers all of the topics from the whole chapter, including Surface Areas And Volumes of cylinder, sphere, etc…. In exercise 13.9 Class 9 Maths, The cuboid is a three-dimensional figure defined by six rectangular planes with different magnitudes of length, width, and height. It has eight vertices and twelve edges, and opposite faces are always equal. Also a sphere is a three-dimensional object that is circular in shape. The cuboid has two different types of surface area. They are lateral surface area and total surface area. Similarly, The surface area of a sphere refers to the overall area covered by its surface in three-dimensional space.

This Story also Contains
  1. Surface Area and Volumes Class 9 Maths Chapter 13 Exercise: 13.9
  2. More About NCERT Solutions for Class 9 Maths Exercise 13.9
  3. Benefits of NCERT Solutions for Class 9 Maths Exercise 13.9
  4. NCERT Solutions of Class 10 Subject Wise

NCERT solutions for Class 9 Maths chapter 13 exercise 13.9 include three questions that are not crucial for the examination but will help to improve geometrical concepts and creative thinking skills, which will be a useful addition to mathematical knowledge. The following exercises are also present along with NCERT book Class 9 Maths chapter 13 exercise 13.9.

Surface Area and Volumes Class 9 Maths Chapter 13 Exercise: 13.9

Q1 A wooden bookshelf has external dimensions as follows: Height \small =110\hspace{1mm}cm , Depth \small =25\hspace{1mm}cm , Breadth \small =85\hspace{1mm}cm (see Fig. \small 13.31 ). The thickness of the plank is \small 5\hspace{1mm}cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is \small 20\hspace{1mm} paise per \small cm^2 and the rate of painting is \small 10\hspace{1mm} paise per \small cm^2 , find the total expenses required for polishing and painting the surface of the bookshelf.

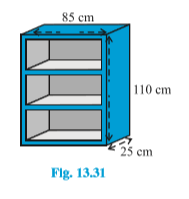
1640848333224

Answer:

External dimension od the bookshelf = 85\ cm\times25\ cm\times110\ cm

(Note: There is no front face)

The external surface area of the shelf = lh + 2 (lb + bh)
\\ = [85 \times 110 + 2 (85 \times 25 + 25 \times 110)] \\ = (9350 + 9750) \\ = 19100\ cm^2

We know, each stripe on the front surface is also to be polished. which is 5 cm stretch.

Area of front face = [85 \times 110 - 75 \times 100 + 2 (75 \times5)]

\\ = 1850 + 750 \\ = 2600\ cm^2

Area to be polished = (19100 + 2600) = 21700\ cm^2

Cost of polishing 1\ cm^2 area = Rs\ 0.20

Cost of polishing 21700\ cm^2 area = Rs.\ (21700 \times 0.20) = Rs.\ 4340

Now,

Dimension of inner part = 75\ cm\times15\ cm\times100\ cm

Area to be painted in 3 rows = 3\times[2 (l + h) b + lh]

\\ =3\times [2 (75 + 30) \times 20 + 75 \times 30] \\ = 3\times[(4200 + 2250)] \\ = 3\times6450 \\ = 19350\ cm^2

Cost of painting 1\ cm^2 area = Rs\ 0.10

Cost of painting 19350\ cm^2 area = Rs.\ (19350 \times 0.10)= Rs.\ 1935

Total expense required for polishing and painting = Rs.\ (4340 + 1935)

= Rs.\ 6275

Q2 The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in Fig \small 13.32 . Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius \small 1.5\hspace{1mm}cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per \small cm^2 and black paint costs 5 paise per \small cm^2 .

1640848312910

Answer:

Given,

The radius of the wooden spheres = r_1 = \frac{21}{2}\ cm

\therefore The surface area of a single sphere = 4\pi r_1^2

\\ = 4\times\frac{22}{7}\times\frac{21}{2}\times\frac{21}{2} \\ = 22\times3\times21

= 1386\ cm^2

Again, the Radius of the cylinder support = \small r_2 = 1.5\hspace{1mm}cm

Height of the support = h = 7\ cm

\therefore The base area of the cylinder = \pi r_2^2 = \frac{22}{7}\times1.5\times1.5 = 7.07\ cm^2

Now, Cost of painting 1\ cm^2 silver = 25\ paise = Rs.\ 0.25

\therefore Cost of painting 1 wooden sphere = Cost of painting (1386-7.07)\ cm^2 silver

= Rs. (0.25\times1378.93) = Rs.\ 344.7325

Now, Curved surface area of the cylindrical support = 2\pi r_2 h

\\ = 2\times\frac{22}{7}\times1.5\times7 \\ = 22\times3 \\ = 66\ cm^2

Now, Cost of painting 1\ cm^2 black = 5\ paise = Rs.\ 0.05

\therefore Cost of painting 1 such stand = Cost of painting 66\ cm^2 silver = Rs. (0.05\times66) = Rs.\ 3.3

\therefore The total cost of painting 1 sphere and its support = Rs.\ (344.7325+3.3) = Rs.\ 348.0325

Therefore, total cost of painting 8 such spheres and their supports = Rs.\ (8\times348.0325) = Rs.\ 2784.26

Q3 The diameter of a sphere is decreased by \small 25\% . By what per cent does its curved surface area decrease?

Answer:

Let the radius of the sphere be r

Diameter of the sphere = 2r

According to question,

Diameter is decreased by \small 25\%

So, the new diameter = \frac{3}{4}\times2r = \frac{3r}{2}

So, the new radius = r' = \frac{3r}{4}

\therefore New surface area = 4\pi r'^2 = 4\pi (\frac{3r}{4})^2

\therefore Decrease in surface area = 4\pi r^2 - 4\pi (\frac{3r}{4})^2

= 4\pi r^2[1 -\frac{9}{16} ]

= 4\pi r^2[\frac{7}{16} ]

\therefore Percentage decrease in the surface area = \frac{Difference\ in\ areas}{Original\ surface\ area}

= \frac{4\pi r^2[\frac{7}{16}]}{4\pi r^2}\times100 \%

= \frac{7}{16}\times100 \%

= 43.75 \%

More About NCERT Solutions for Class 9 Maths Exercise 13.9

In NCERT solutions for Class 9 Maths exercise 13.9, The cuboid’s total surface area may be computed by summing the areas of the 6 rectangular faces, where the area is calculated by multiplying the length and breadth of each surface. 2(lb + bh + hl) = TSA. A cuboid’s lateral surface area can be computed by summing the four planes of a rectangle and subtracting the upper and lower surfaces. 2h(l + b) = LSA. The product of four times the area of the circle is used to compute the sphere’s surface area. A=4πr2. A cube is a three-dimensional shape with six faces, eight vertices, and twelve edges that has the same length, width, and height. The cube’s surface area is 6a2, where a is the length of one of its sides.

Also Read| Surface Areas And Volumes Class 9 Notes

Benefits of NCERT Solutions for Class 9 Maths Exercise 13.9

• NCERT solutions for Class 9 Maths exercise 13.9 helps in solving the application level complex problem in an easy way and get sufficient practice to solve the questions confidently.

• By solving the NCERT solution for Class 9 Maths chapter 13 exercise 13.9 exercises, we can get an overall understanding of the concepts and helps us to be familiar with the different types of questions in the exam

• Exercise 13.9 Class 9 Maths, helps to increase your accuracy and speed in solving problems.

Also, See:

NCERT Solutions of Class 10 Subject Wise

Frequently Asked Question (FAQs)

1. A cuboid's lateral surface area is ________

A cuboid's lateral surface area is 2h(l + b) 

2. The cuboid's total surface area is _______

 TSA = 2(lb + bh + hl) is the total surface area of a cuboid . 

3. The sphere's surface area is _________

The sphere's surface area is 4πr^2 . 

4. The surface area of the cube with the edge m is ______

The surface area of the cube with the edge m is 6m^2 

5. Define cube.

A cube is a three-dimensional shape with the same length, breadth, and height as it has six faces, eight vertices, and twelve edges. 


6. Define the radius of the sphere using the NCERT solutions for Class 9 Maths chapter 13 exercise 13.9 .

 NCERT solutions for Class 9 Maths chapter 13 exercise 13.9 are as follows: The distance between a sphere's surface and its centre is its radius. 

7. Write the relationship between radius and diameter.

The radius of a circle is twice its diameter . 2×radius = diameter

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Madhya Pradesh Board 10th Examination

Application Date:01 May,2024 - 20 May,2024

Madhya Pradesh Board 12th Examination

Application Date:01 May,2024 - 20 May,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

ALLEN NEET Coaching
ALLEN NEET Coaching
Apply

Ace your NEET preparation with ALLEN Online Programs

View All Application Forms
News and Notifications
Barmer teacher suspended for slapping class 3 student
01/05/2024, 17:07:10
Teacher arrested for `sexual exploitation' at Ujjain Ashram school
01/05/2024, 14:28:18
Delhi NCR schools get bomb threat; fire tender arrives, search underway
01/05/2024, 04:09:04
Education is greatest gift to society: Vice President Jagdeep Dhankhar
30/04/2024, 17:02:12
Jharkhand schools up to Class 8 closed till further orders due to heat wave
30/04/2024, 11:49:37
Delhi School EWS Admission 2024-25: Registration window opens at edudel.nic.in; eligibility
30/04/2024, 09:27:25
Education ministry asks NCERT to review, update textbooks on yearly basis
29/04/2024, 12:22:03
Back to top