NCERT Solutions for Exercise 13.2 Class 9 Maths Chapter 13

Q: The number of surfaces in the right cylinder is ______

4 3 2 1 Solution : The number of surfaces in the right cylinder is 3 . Option (b) 3

NCERT Solutions for Exercise 13.2 Class 9 Maths Chapter 13 - Surface Area and Volumes

Edited By Vishal kumar | Updated on Oct 13, 2023 09:11 AM IST

NCERT Solutions for Class 9 Maths Exercise 13.2 Chapter 13 Surface Areas And Volumes- Download Free PDF

NCERT Solutions for Class 9 Maths Exercise 13.2 Chapter 13 Surface Areas And Volumes- NCERT Solutions for Class 9 Maths Exercise 13.2 deals with the concept of the right circular cylinder and its surface areas. A right circular cylinder is a cylinder with a closed circular surface, two parallel bases on both ends and elements that are perpendicular to the base. Three pieces make up the right circular cylinder. They are

Don't Miss: JEE Main 2027: Narayana Scholarship Test Preparation Kit for Class 9

This Story also Contains

NCERT Solutions for Class 9 Maths Exercise 13.2 Chapter 13 Surface Areas And Volumes- Download Free PDF
Download PDF of NCERT Solutions for Class 9 Maths Chapter 13 – Surface Areas and Volumes Exercise 13.2
Access Surface Area and Volumes Class 9 Chapter 13 Exercise: 13.2
More about NCERT Solutions for Class 9 Maths Exercise 13.2 :
Benefits of NCERT Solutions for Class 9 Maths Exercise 13.2 :
Key Features of 9th Class Maths Exercise 13.2 Answers
NCERT Solutions of Class 10 Subject Wise

NCERT Solutions for Exercise 13.2 Class 9 Maths Chapter 13 - Surface Area and Volumes

Top circular base
Curved lateral face
Bottom circular face

In exercise 13.2 Class 9 Maths, A combination of two circles plus a rectangle forms the right circular cylinder. The surface area of a right circular cylinder is the area covered by the surface of the right circular cylinder. Surface area can be divided into two categories. They are

Lateral Surface Area
Total Surface Area

The curved surface area of the right circular cylinder, also known as the lateral surface area of the right circular cylinder, is the area covered by the curved surface of the cylinder. The total surface area of the right circular cylinder is the area occupied by the complete cylinder. NCERT solutions for Class 9 Maths chapter 13 exercise 13.2 consists of 11 questions which are direct formula based questions. The concepts related to the surface area and volumes are well explained in this NCERT syllabus 9th class maths exercise 13.2 answers . Along with NCERT book Class 9 Maths chapter 13 exercise 13.2 the following exercises are also present.

***According to the CBSE Syllabus 2023-24, this chapter is now Chapter 11.

Download PDF of NCERT Solutions for Class 9 Maths Chapter 13 – Surface Areas and Volumes Exercise 13.2

Download PDF

Access Surface Area and Volumes Class 9 Chapter 13 Exercise: 13.2

Q1 The curved surface area of a right circular cylinder of height $\small 14\hspace{1mm}cm$ is $\small 88\hspace{1mm}cm^2$ . Find the diameter of the base of the cylinder.

Answer:

Given,

The curved surface area of the cylinder = 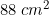$\small 88\hspace{1mm}cm^2$

And, the height of the cylinder, 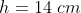$h= 14\ cm$

We know, Curved surface area of a right circular cylinder = 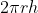$2\pi rh$

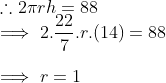
$\\ \therefore 2\pi rh = 88 \\ \implies 2.\frac{22}{7}. r. (14) = 88 \\ \\ \implies r = 1$

Therefore, the diameter of the cylinder = $1\ cm$

Q2 It is required to make a closed cylindrical tank of height $\small 1\hspace{1mm}m$ and base diameter $\small 140\hspace{1mm}cm$ from a metal sheet. How many square metres of the sheet are required for the same?

Answer:

Given,

Height of the cylindrical tank = $h = 1\ m$

Base diameter = $\small d = 140\ cm = 1.4\ m$

We know,

The total surface area of a cylindrical tank = $\small 2\pi r h+2\pi r^2 = 2\pi r(r+h)$

$\small = 2.\frac{22}{7}. \frac{1.4}{2}.(0.7+1) = 2.\frac{22}{7}. (0.7).(1.7)$

$\small = 44\times0.17$

$\small = 7.48\ m^2$

Therefore, square metres of the sheet is $\small 7.48\ m^2$

Q3 (i) A metal pipe is $\small 77\hspace{1mm}cm$ long. The inner diameter of a cross section is $\small 4\hspace{1mm}cm$ , the outer diameter being $\small 4.4\hspace{1mm}cm$ (see Fig. $\small 13.11$ ). Find its inner curved surface area,

1640846782195

Answer:

Note: There are two surfaces, inner and outer.

Given,

Height of the cylinder, $h = 77\ cm$

Outer diameter = $r_1 = 4.4\ cm$

Inner diameter = $r_2 = 4\ cm$

Inner curved surface area = $2\pi r_2h$

$\\ = 2\times\frac{22}{7}\times2\times77 \\ = 968\ cm^2$

Therefore, the inner curved surface area of the cylindrical pipe is $968\ cm^2$

Q3 (ii) A metal pipe is $\small 77\hspace{1mm}cm$ long. The inner diameter of a cross section is $\small 4\hspace{1mm}cm$ , the outerdiameter being $\small 4.4\hspace{1mm}cm$ (see Fig. $\small 13.11$ ). Find its outer surface area.

1640846815255

Answer:

Note: There are two surfaces, inner and outer.

Given,

Height of the cylinder, $h = 77\ cm$

Outer diameter = $r_1 = 4.4\ cm$

Inner diameter = $r_2 = 4\ cm$

Outer curved surface area = $2\pi r_1h$

$\\ = 2\times\frac{22}{7}\times2.2\times77 \\ = 1064.8\ cm^2$

Therefore, the outer curved surface area of the cylindrical pipe is $1064.8\ cm^2$

Q3 (iii) A metal pipe is $\small 77\hspace{1mm}cm$ long. The inner diameter of a cross section is 4 cm, the outer diameter being $\small 4.4 \hspace{1mm}cm$ (see Fig. $\small 13.11$ ). Find its total surface area.

1640846851383

Answer:

Note: There are two surfaces, inner and outer.

Given,

Height of the cylinder, $h = 77\ cm$

Outer diameter = $r_1 = 4.4\ cm$

Inner diameter = $r_2 = 4\ cm$

Outer curved surface area = $2\pi r_1h$

Inner curved surface area = $2\pi r_2h$

Area of the circular rings on top and bottom = $2\pi(r_2^2-r_1^2)$

$\therefore$ The total surface area of the pipe = $2\pi r_1h +2\pi r_2h+ 2\pi(r_2^2-r_1^2)$

$\\ = [968 + 1064.8 + 2\pi {(2.2)^2 - (2)^2}]\\ \\ = (2032.8 + 2\times \frac{22}{7}\times 0.84) \\ \\ = (2032.8 + 5.28) \\ = 2038.08\ cm^2$

Therefore, the total surface area of the cylindrical pipe is $2038.08\ cm^2$

Q4 The diameter of a roller is $\small 84\hspace{1mm}cm$ and its length is $\small 120\hspace{1mm}cm$ . It takes $\small 500$ complete revolutions to move once over to level a playground. Find the area of the playground in $\small m^2$ .

Answer:

Given,

The diameter of the cylindrical roller = $\small d = 84\hspace{1mm}cm$

Length of the cylindrical roller = $\small h = 120\hspace{1mm}cm$

The curved surface area of the roller = $2\pi r h = \pi dh$

$\\ = \frac{22}{7}\times84\times120 \\ \\ = 31680\ cm^2$

$\therefore$ Area of the playground = $Area\ covered\ in\ 1\ rotation \times500$

$\\ = 31680 \times500 \\ = 15840000 cm^2 \\ = 1584\ m^2$

Therefore, the required area of the playground = $1584\ m^2$

Q5 A cylindrical pillar is $\small 50\hspace{1mm}cm$ in diameter and $3.5\ m$ in height. Find the cost of painting the curved surface of the pillar at the rate of $\small Rs \hspace{1mm} 12.50$ per $\small m^2$ .

Answer:

Given,

Radius of the cylindrical pillar, r = $\frac{50}{2}\ cm= 25\ cm= 0.25\ m$

Height of the cylinder, h = $3.5\hspace{1mm}m$

We know,

Curved surface area of a cylinder = $2\pi r h$

$\therefore$ Curved surface area of the pillar = $2\times\frac{22}{7}\times 0.25 \times3.5$

$= 1\times22\times 0.25\ m^2$

$= 5.5\ m^2$

Now,

Cost of painting $\small 1\ m^2$ of the pillar = $\small Rs \hspace{1mm} 12.50$

$\therefore$ Cost of painting the curved surface area of the pillar = $\small Rs.\ (12.50\times5.5)$

$\small = Rs.\ 68.75$

Therefore, the cost of painting curved surface area of the pillar is $\small Rs.\ 68.75$

Q6 Curved surface area of a right circular cylinder is $\small 4.4\hspace{1mm}m^2$ . If the radius of the base of the cylinder is $\small 0.7\hspace{1mm}m$ , find its height.

Answer:

Given, a right circular cylinder

Curved surface area of the cylinder = $\small 4.4\hspace{1mm}m^2$

The radius of the base = $r = 0.7\ m$

Let the height of the cylinder be $h$

We know,

Curved surface area of a cylinder of radius $r$ and height $h$ = $2\pi r h$

$\therefore$ $2\pi r h = 4.4$

$\\ \Rightarrow 2\times\frac{22}{7}\times0.7 \times h = 4.4 \\ \\ \Rightarrow 44\times0.1 \times h = 4.4 \\ \Rightarrow h = 1\ m$

Therefore, the required height of the cylinder is $1\ m$

Q7 (i) The inner diameter of a circular well is $\small 3.5\hspace{1mm}m$ . It is $\small 10\hspace{1mm}m$ deep. Find its inner curved surface area.

Answer:

Given,

The inner diameter of the circular well = $d = \small 3.5\hspace{1mm}m$

Depth of the well = $h = 10\ m$

We know,

The curved surface area of a cylinder = $2\pi rh$

$\therefore$ The curved surface area of the well = $2\times\frac{22}{7}\times\frac{3.5}{2}\times10$

$\\ = 44 \times 0.25 \times 10 \\ = 110\ m^2$

Therefore, the inner curved surface area of the circular well is $110\ m^2$

Q7 (ii) The inner diameter of a circular well is $\small 3.5\hspace{1mm}m$ . It is $\small 10\hspace{1mm}m$ deep. Find the cost of plastering this curved surface at the rate of Rs 40 per $\small m^2$ .

Answer:

Given,

The inner diameter of the circular well = $d = \small 3.5\hspace{1mm}m$

Depth of the well = $h = 10\ m$

$\therefore$ The inner curved surface area of the circular well is $110\ m^2$

Now, the cost of plastering the curved surface per $\small m^2$ = Rs. 40

$\therefore$ Cost of plastering the curved surface of $110\ m^2$ = $Rs.\ (110 \times 40) = Rs.\ 4400$

Therefore, the cost of plastering the well is $Rs.\ 4400$

Q8 In a hot water heating system, there is a cylindrical pipe of length $\small 28\hspace{1mm}m$ and diameter $\small 5\hspace{1mm}cm$ . Find the total radiating surface in the system.

Answer:

Given,

Length of the cylindrical pipe = $l = \small 28\hspace{1mm}m$

Diameter = $\small d = 5\hspace{1mm}cm = 0.05\ m$

The total radiating surface will be the curved surface of this pipe.

We know,

The curved surface area of a cylindrical pipe of radius $r$ and length $l$ = $2\pi r l$

$\therefore$ CSA of this pipe =

$= 2\times\frac{22}{7}\times\frac{0.05}{2}\times28$

$\\ = 22\times0.05\times4 \\ = 4.4\ m^2$

Therefore, the total radiating surface of the system is $4.4\ m^2$

Q9 (i) Find the lateral or curved surface area of a closed cylindrical petrol storage tank that is $\small 4.2\hspace{1mm}m$ in diameter and $\small 4.5\hspace{1mm}m$ high.

Answer:

Given, a closed cylindrical petrol tank.

The diameter of the tank = $\small d = 4.2\hspace{1mm}m$

Height of the tank = $\small h = 4.5\hspace{1mm}m$

We know,

The lateral surface area of a cylinder of radius $\small r$ and height $\small h$ = $\small 2\pi r h$

$\small \therefore$ The lateral surface area of a cylindrical tank = $\small 2\times\frac{22}{7}\times\frac{4.2}{2}\times4.5$

$\small \\ = (44 \times 0.3 \times 4.5) \\ = 59.4\ m^2$

Therefore, the lateral or curved surface area of a closed cylindrical petrol storage tank is $\small 59.4\ m^2$

Q9 (ii) Find: how much steel was actually used, if $\small \frac{1}{12}$ of the steel actually used was wasted in making the tank.

Answer:

Given, a closed cylindrical petrol tank.

The diameter of the tank = $\small d = 4.2\hspace{1mm}m$

Height of the tank = $\small h = 4.5\hspace{1mm}m$

Now, Total surface area of the tank = $2\pi r (r + h)$

$\\ = 2 \times \frac{22}{7} \times 2.1 \times (2.1 + 4.5) \\ = (44 \times 0.3 \times 6.6) \\ = 87.12\ m^2$

Now, let $x\ m^2$ of steel sheet be actually used in making the tank

Since $\small \frac{1}{12}$ of steel was wasted, the left $\small \frac{11}{12}$ of the total steel sheet was used to made the tank.
$\small \therefore$ The total surface area of the tank = $\small \frac{11}{12}\times (Total\ area\ of\ steel\ sheet )$
$\small \\ \Rightarrow 87.12= \frac{11}{12}x \\ \Rightarrow x = \frac{87.12\times12}{11} \\ \Rightarrow x = 95.04\ m^2$

Therefore, $\small 95.04\ m^2$ of steel was actually used in making the tank.

Q10 In Fig. $\small 13.12$ , you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of $\small 20\hspace{1mm}cm$ and height of $\small 30\hspace{1mm}cm$ . A margin of $\small 2.5\hspace{1mm}cm$ is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.

1640846895227

Answer:

Given, a cylindrical lampshade

The diameter of the base = $d = 20\ cm$

Height of the cylinder = $30\ cm$

The total height of lampshade= $(30+ 2.5 + 2.5) = 35\ cm$

We know,

Curved surface area of a cylinder of radius $r$ and height $h$ = $2\pi r h$

Now, Cloth required for covering the lampshade = Curved surface area of the cylinder

$\\ = 2\times\frac{22}{7} \times10 \times 35 \\ \\ = 22\times10\times10 = 2200\ cm^2$

Therefore, $2200\ cm^2$ cloth will be required for covering the lampshade.

Q11 The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius $\small 3\hspace{1mm}cm$ and height $\small 10.5\hspace{1mm}cm$ . The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?

Answer:

Given, a cylinder with a base.

The radius of the cylinder = $r = 3\ cm$

Height of the cylinder = $h = 10.5\ cm$

We know,

The lateral surface area of a cylinder of radius $r$ and height $h$ = $2\pi r h$

$\therefore$ Area of the cylindrical penholder = Lateral areal + Base area

$= 2\pi r h + \pi r^2 = \pi r (2h+r)$

$= \frac{22}{7}\times3\times[2(10.5)+3]$

$\\ = \frac{22}{7}\times3\times[24] \\ \\ = \frac{1584}{7}\ cm^2$
Area of 35 penholders = $\frac{1584}{7}\times35\ cm^2$

$= 7920\ cm^2$

Therefore, the area of carboard required is $7920\ cm^2$

Benefits of NCERT Solutions for Class 9 Maths Exercise 13.2 :

• NCERT solutions for Class 9 Maths Exercise 13.2 gives a clear outline of the right circular cylinder in detail so that we get a clear understanding of what it is.

• By answering the NCERT solution for Class 9 Maths chapter 13 exercise 13.2 exercises, we can improve our grades in the first and second terms of school, as well as in our higher education.

• In exercise 13.2 Class 9 Maths, The formulas for calculating surface areas and volume for the right circular cylinder are well explained and these formulas will help in solving the competitive questions, hence we must make a note of those formulas.

Key Features of 9th Class Maths Exercise 13.2 Answers

Step-by-Step Solutions: The NCERT Solutions fo class 9 ex 13.2 provide detailed, step-by-step explanations for each problem, making it easier for students to grasp the concepts.
Practical Application: This exercise presents practical problems that require students to calculate surface areas and volumes of various 3D shapes, honing their problem-solving skills.
Clear and Understandable Language: Class 9 maths ex 13.2 Solutions are presented in clear and understandable language, ensuring that students can comprehend the concepts with ease.
PDF Format: Students can access the ex 13.2 class 9 solutions in PDF format, enabling them to download and use the materials offline, making learning convenient and accessible.
Foundation for Advanced Geometry: Mastery of surface areas and volumes of 3D shapes in this exercise prepares students for more complex geometry topics they will study in higher classes.

Also See:

NCERT Solutions of Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. Define the right circular cylinder, according to NCERT solutions for Class 9 Maths chapter 13 exercise 13.2 .

Solution :

A right circular cylinder has a closed circular surface with two parallel bases on both ends and elements that are perpendicular to its base, according to NCERT solutions for Class 9 Maths chapter 13 exercise 13.2.

2. How many parts are there in the right circular cylinder and what are they?

Solution :

The right circular cylinder is divided into three parts. They are

Top circular base
Curved lateral face
Bottom circular face

3. What are the types of surface area?

Solution :

There are two types of surface area . They are

Lateral Surface Area
Total Surface Area

4. Define the lateral surface area of the right circular cylinder.

Solution :

The area covered by the curved surface of the cylinder is known as the curved surface area of the right circular cylinder which is often referred as lateral surface area of the right circular cylinder.

5. The lateral surface area of the right circular cylinder is ________

Solution :

The lateral surface area of the right circular cylinder is 2πrh

6. The total surface area of the right circular cylinder is ________

Solution :

The right circular cylinder has a total surface area of 2πr(h+r)

7. The surface areas are calculated in _______ units

Solution :

The surface areas are measured in terms of square units .

8. A closed right circular cylinder's total surface area is equal to the sum of ________

Solution :

The area of the lateral surface plus the area of the two bases equals the total surface area of a closed right circular cylinder.

9. The number of surfaces in the right cylinder is ______

Solution :

The number of surfaces in the right cylinder is 3 . Option (b) 3

10. According to NCERT solutions for Class 9 Maths chapter 13 exercise 13.2 ,How is the total surface area calculated from the lateral surface area and area of the circle?

Solution :

The total surface area of a closed right circular cylinder is computed by adding the area of the lateral surface and the area of the two bases, according to NCERT solutions for Class 9 Maths chapter 13 exercise 13.2 .

TSA=CAS+2(Area of a circle)

= 2πrh+2π(r^2)

TSA=2πr(h+r)

Also Read

NCERT Solutions for Class 9 - Subject-wise PDFs Updated for 2024-25

NCERT Solutions for Class 9 Science

NCERT Solutions for Class 9 Maths

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

IGNOU Assignment Result 2024

Dec 21, 2024

DBSE Time Table 2025, Check Delhi Board Exam Schedule for Class 10 & 12

Dec 20, 2024

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Exercise 13.2 Class 9 Maths Chapter 13 - Surface Area and Volumes

NCERT Solutions for Class 9 Maths Exercise 13.2 Chapter 13 Surface Areas And Volumes- Download Free PDF

Download PDF of NCERT Solutions for Class 9 Maths Chapter 13 – Surface Areas and Volumes Exercise 13.2

Access Surface Area and Volumes Class 9 Chapter 13 Exercise: 13.2

More about NCERT Solutions for Class 9 Maths Exercise 13.2 :

Benefits of NCERT Solutions for Class 9 Maths Exercise 13.2 :

Key Features of 9th Class Maths Exercise 13.2 Answers

NCERT Solutions of Class 10 Subject Wise

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Means Cum-Merit Scholarship

Gujarat Board Higher Secondary School Certificate

Madhya Pradesh State Open School 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app