NCERT Solutions for Exercise 6.5 Class 10 Maths Chapter 6 - Triangles
NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.5 Triangles
NCERT Solutions for Exercise 6.5 Class 10 Maths Chapter 6 Triangles are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 maths ex 6.5 introduces the concept of similar triangles having an angle of 90 degree. In NCERT solutions for Class 10 Maths chapter 6 exercise 6.5 three theorems are given which explains some important concepts of the right-angled triangle. In NCERT book Class 10 Maths, theorem 6.7 states that “if a perpendicular is drawn from the vertex of a right-angle triangle to the hypotenuse, and then triangles on both sides of the perpendicular are comparable to each other and to the total triangle”. The above-stated theorem of NCERT syllabus Class 10 Maths chapter 6 can be used to prove the Pythagoras theorem.
10th class Maths exercise 6.5 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.
Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 6 exercise 6.5
Assess NCERT Solutions for Class 10 Maths chapter 6 exercise 6.5
Triangles Class 10 Chapter 6 Exercise: 6.5
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 7 cm, 24 cm
By Pythagoras theorem,
$h^2=7^2+24^2$
$h^2=49+576$
$h^2=625$
$h=25$ = given third side.
Hence, it is the right triangle with h=25 cm.
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 3 cm, 6 cm
By Pythagoras theorem,
$h^2=3^2+6^2$
$h^2=9+36$
$h^2=45$
$h=\sqrt{45}\neq 8$
Hence, it is not the right triangle.
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 50 cm, 80 cm
By Pythagoras theorem,
$h^2=50^2+80^2$
$h^2=2500+6400$
$h^2=8900$
$h=\sqrt{8900}\neq 100$
Hence, it is not a right triangle.
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 5cm, 12 cm
By Pythagoras theorem,
$h^2=5^2+12^2$
$h^2=25+144$
$h^2=169$
$h=13$ = given third side.
Hence, it is a right triangle with h=13 cm.
Answer:
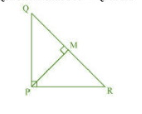
Let $\angle MPR$ be x
In $\triangle MPR$ ,
$\angle MRP=180 ^\circ-90 ^\circ-x$
$\angle MRP=90 ^\circ-x$
Similarly,
In $\triangle MPQ$ ,
$\angle MPQ=90 ^\circ-\angle MPR$
$\angle MPQ=90 ^\circ-x$
$\angle MQP=180 ^\circ-90 ^\circ-(90 ^\circ-x)=x$
In $\triangle QMP\, and\, \triangle PMR,$
$\angle MPQ\, =\angle MRP$
$\angle PMQ\, =\angle RMP$
$\angle MQP\, =\angle MPR$
$\triangle QMP\, \sim \triangle PMR,$ (By AAA)
$\frac{QM}{PM}=\frac{MP}{MR}$
$\Rightarrow PM^2=MQ\times MR$
Hence proved.
Q3 (1) In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that $AB^2 = BC . BD .$
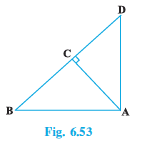
Answer:
In $\triangle ADB\, and\, \triangle ABC,$
$\angle DAB\, =\angle ACB \, \, \, \, \, \, \, \, (Each 90 ^\circ)$
$\angle ABD\, =\angle CBA$ (common )
$\triangle ADB\, \sim \triangle ABC$ (By AA)
$\Rightarrow \frac{AB}{BC}=\frac{BD}{AB}$
$\Rightarrow AB^2=BC.BD$ , hence prooved .
Q3 (2) In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that $AC^2 = BC . DC .$
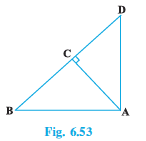
Answer:
Let $\angle CAB$ be x
In $\triangle ABC$ ,
$\angle CBA=180 ^\circ-90 ^\circ-x$
$\angle CBA=90 ^\circ-x$
Similarly,
In $\triangle CAD$ ,
$\angle CAD=90 ^\circ-\angle CAB$
$\angle CAD=90 ^\circ-x$
$\angle CDA=180 ^\circ-90 ^\circ-(90 ^\circ-x)=x$
In $\triangle ABC\, and\, \triangle ACD,$
$\angle CBA\, =\angle CAD$
$\angle CAB\, =\angle CDA$
$\angle ACB\, =\angle DCA$ ( Each right angle)
$\triangle ABC\, \sim \triangle ,ACD$ (By AAA)
$\frac{AC}{DC}=\frac{BC}{AC}$
$\Rightarrow AC^2=BC\times DC$
Hence proved
Q3 (3) In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that $AD^2 = BD . CD .$
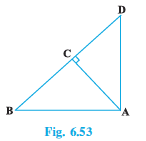
Answer:
In $\triangle ACD\, and\, \triangle ABD,$
$\angle DCA\, =\angle DAB\, \, \, \, \, \, \, \, (Each 90 ^\circ)$
$\angle CDA\, =\angle ADB$ (common )
$\triangle ACD\, \sim \triangle ABD$ (By AA)
$\Rightarrow \frac{CD}{AD}=\frac{AD}{BD}$
$\Rightarrow AD^2=BD\times CD$
Hence proved.
Q4 ABC is an isosceles triangle right angled at C. Prove that $AB^2 = 2AC ^2$
Answer:
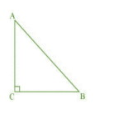
Given: ABC is an isosceles triangle right angled at C.
Let AC=BC
In $\triangle$ ABC,
By Pythagoras theorem
$AB^2=AC^2+BC^2$
$AB^2=AC^2+AC^2$ (AC=BC)
$AB^2=2.AC^2$
Hence proved.
Answer:
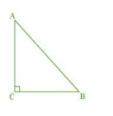
Given: ABC is an isosceles triangle with AC=BC.
In $\triangle$ ABC,
$AB^2=2.AC^2$ (Given )
$AB^2=AC^2+AC^2$ (AC=BC)
$AB^2=AC^2+BC^2$
These sides satisfy Pythagoras theorem so ABC is a right-angled triangle.
Hence proved.
Q6 ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Answer:
Given: ABC is an equilateral triangle of side 2a.
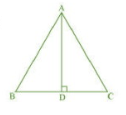
AB=BC=AC=2a
AD is perpendicular to BC.
We know that the altitude of an equilateral triangle bisects the opposite side.
So, BD=CD=a
In $\triangle$ ADB,
By Pythagoras theorem,
$AB^2=AD^2+BD^2$
$\Rightarrow (2a)^2=AD^2+a^2$
$\Rightarrow 4a^2=AD^2+a^2$
$\Rightarrow 4a^2-a^2=AD^2$
$\Rightarrow 3a^2=AD^2$
$\Rightarrow AD=\sqrt{3}a$
The length of each altitude is $\sqrt{3}a$ .
Answer:
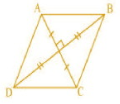
In $\triangle$ AOB, by Pythagoras theorem,
$AB^2=AO^2+BO^2..................1$
In $\triangle$ BOC, by Pythagoras theorem,
$BC^2=BO^2+CO^2..................2$
In $\triangle$ COD, by Pythagoras theorem,
$CD^2=CO^2+DO^2..................3$
In $\triangle$ AOD, by Pythagoras theorem,
$AD^2=AO^2+DO^2..................4$
Adding equation 1,2,3,4,we get
$AB^2+BC^2+CD^2+AD^2=AO^2+BO^2+BO^2+CO^2+CO^2+DO^2+AO^2+DO^2$
$AB^2+BC^2+CD^2+AD^2=2(AO^2+BO^2+CO^2+DO^2)$
$\Rightarrow AB^2+BC^2+CD^2+AD^2=2(2.AO^2+2.BO^2)$ (AO=CO and BO=DO)
$\Rightarrow AB^2+BC^2+CD^2+AD^2=4(AO^2+BO^2)$
$\Rightarrow AB^2+BC^2+CD^2+AD^2=4((\frac{AC}{2})^2+(\frac{BD}{2})^2)$
$\Rightarrow AB^2+BC^2+CD^2+AD^2=4((\frac{AC^2}{4})+(\frac{BD^2}{4}))$
$\Rightarrow AB^2+BC^2+CD^2+AD^2=AC^2+BD^2$
Hence proved .
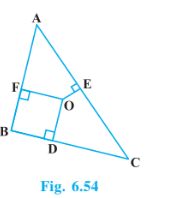
Answer:
Join AO, BO, CO
In $\triangle$ AOF, by Pythagoras theorem,
$OA^2=OF^2+AF^2..................1$
In $\triangle$ BOD, by Pythagoras theorem,
$OB^2=OD^2+BD^2..................2$
In $\triangle$ COE, by Pythagoras theorem,
$OC^2=OE^2+EC^2..................3$
Adding equation 1,2,3,we get
$OA^2+OB^2+OC^2=OF^2+AF^2+OD^2+BD^2+OE^2+EC^2$ $\Rightarrow OA^2+OB^2+OC^2-OD^2-OE^2-OF^2=AF^2+BD^2+EC^2....................4$
Hence proved
Q8 (2) In Fig. 6.54, O is a point in the interior of a triangle ABC, OD $\perp$ BC, OE $\perp$ AC and OF $\perp$ AB. $AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2.$
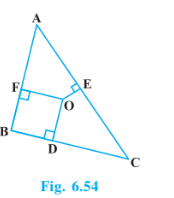
Answer:
Join AO, BO, CO
In $\triangle$ AOF, by Pythagoras theorem,
$OA^2=OF^2+AF^2..................1$
In $\triangle$ BOD, by Pythagoras theorem,
$OB^2=OD^2+BD^2..................2$
In $\triangle$ COE, by Pythagoras theorem,
$OC^2=OE^2+EC^2..................3$
Adding equation 1,2,3,we get
$OA^2+OB^2+OC^2=OF^2+AF^2+OD^2+BD^2+OE^2+EC^2$ $\Rightarrow OA^2+OB^2+OC^2-OD^2-OE^2-OF^2=AF^2+BD^2+EC^2....................4$
$\Rightarrow (OA^2-OE^2)+(OC^2-OD^2)+(OB^2-OF^2)=AF^2+BD^2+EC^2$ $\Rightarrow AE^2+CD^2+BF^2=AF^2+BD^2+EC^2$
Answer:
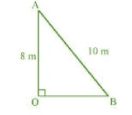
OA is a wall and AB is a ladder.
In $\triangle$ AOB, by Pythagoras theorem
$AB^2=AO^2+BO^2$
$\Rightarrow 10^2=8^2+BO^2$
$\Rightarrow 100=64+BO^2$
$\Rightarrow 100-64=BO^2$
$\Rightarrow 36=BO^2$
$\Rightarrow BO=6 m$
Hence, the distance of the foot of the ladder from the base of the wall is 6 m.
Answer:
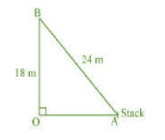
OB is a pole.
In $\triangle$ AOB, by Pythagoras theorem
$AB^2=AO^2+BO^2$
$\Rightarrow 24^2=18^2+AO^2$
$\Rightarrow 576=324+AO^2$
$\Rightarrow 576-324=AO^2$
$\Rightarrow 252=AO^2$
$\Rightarrow AO=6\sqrt{7} m$
Hence, the distance of the stack from the base of the pole is $6\sqrt{7}$ m.
Answer:
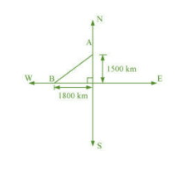
Distance travelled by the first aeroplane due north in $1\frac{1}{2}$ hours.
$=1000\times \frac{3}{2}=1500 km$
Distance travelled by second aeroplane due west in $1\frac{1}{2}$ hours.
$=1200\times \frac{3}{2}=1800 km$
OA and OB are the distance travelled.
By Pythagoras theorem,
$AB^2=OA^2+OB^2$
$\Rightarrow AB^2=1500^2+1800^2$
$\Rightarrow AB^2=2250000+3240000$
$\Rightarrow AB^2=5490000$
$\Rightarrow AB^2=300\sqrt{61}km$
Thus, the distance between the two planes is $300\sqrt{61}km$ .
Answer:
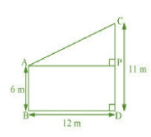
Let AB and CD be poles of heights 6 m and 11 m respectively.
CP=11-6=5 m and AP= 12 m
In $\triangle$ APC,
By Pythagoras theorem,
$AP^2+PC^2=AC^2$
$\Rightarrow 12^2+5^2=AC^2$
$\Rightarrow 144+25=AC^2$
$\Rightarrow 169=AC^2$
$\Rightarrow AC=13m$
Hence, the distance between the tops of two poles is 13 m.
Answer:
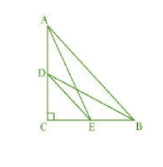
In $\triangle$ ACE, by Pythagoras theorem,
$AE^2=AC^2+CE^2..................1$
In $\triangle$ BCD, by Pythagoras theorem,
$DB^2=BC^2+CD^2..................2$
From 1 and 2, we get
$AC^2+CE^2+BC^2+CD^2=AE^2+DB^2..................3$
In $\triangle$ CDE, by Pythagoras theorem,
$DE^2=CD^2+CE^2..................4$
In $\triangle$ ABC, by Pythagoras theorem,
$AB^2=AC^2+CB^2..................5$
From 3,4,5 we get
$DE^2+AB^2=AE^2+DB^2$
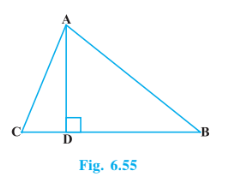
Answer:
In $\triangle$ ACD, by Pythagoras theorem,
$AC^2=AD^2+DC^2$
$AC^2-DC^2=AD^2..................1$
In $\triangle$ ABD, by Pythagoras theorem,
$AB^2=AD^2+BD^2$
$AB^2-BD^2=AD^2.................2$
From 1 and 2, we get
$AC^2-CD^2=AB^2-DB^2..................3$
Given : 3DC=DB, so
$CD=\frac{BC}{4}\, \, and\, \, BD=\frac{3BC}{4}........................4$
From 3 and 4, we get
$AC^2-(\frac{BC}{4})^2=AB^2-(\frac{3BC}{4})^2$
$AC^2-(\frac{BC^2}{16})=AB^2-(\frac{9BC^2}{16})$
$16AC^2-BC^2=16AB^2- 9BC^2$
$16AC^2=16AB^2- 8BC^2$
$\Rightarrow 2AC^2=2AB^2- BC^2$
$2 AB^2 = 2 AC^2 + BC^2.$
Hence proved.
Answer:

Given: An equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC.
To prove : $9 AD^2 = 7 AB^2$
Let AB=BC=CA=a
Draw an altitude AE on BC.
So, $BE=CE=\frac{a}{2}$
In $\triangle$ AEB, by Pythagoras theorem
$AB^2=AE^2+BE^2$
$a^2=AE^2+(\frac{a}{2})^2$
$\Rightarrow a^2-(\frac{a^2}{4})=AE^2$
$\Rightarrow (\frac{3a^2}{4})=AE^2$
$\Rightarrow AE=(\frac{\sqrt{3}a}{2})$
Given : BD = 1/3 BC.
$BD=\frac{a}{3}$
$DE=BE=BD=\frac{a}{2}-\frac{a}{3}=\frac{a}{6}$
In $\triangle$ ADE, by Pythagoras theorem,
$AD^2=AE^2+DE^2$
$\Rightarrow AD^2=(\frac{\sqrt{3}a}{2})^2+(\frac{a}{6})^2$
$\Rightarrow AD^2=(\frac{3a^2}{4})+(\frac{a^2}{36})$
$\Rightarrow AD^2=(\frac{7a^2}{9})$
$\Rightarrow AD^2=(\frac{7AB^2}{9})$
$\Rightarrow 9AD^2=7AB^2$
Answer:
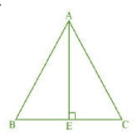
Given: An equilateral triangle ABC.
Let AB=BC=CA=a
Draw an altitude AE on BC.
So, $BE=CE=\frac{a}{2}$
In $\triangle$ AEB, by Pythagoras theorem
$AB^2=AE^2+BE^2$
$a^2=AE^2+(\frac{a}{2})^2$
$\Rightarrow a^2-(\frac{a^2}{4})=AE^2$
$\Rightarrow (\frac{3a^2}{4})=AE^2$
$\Rightarrow 3a^2=4AE^2$
$\Rightarrow 4.(altitude)^2=3.(side)^2$
Q17 Tick the correct answer and justify : In $\Delta ABC$ AB = $6 \sqrt 3$ cm, AC = 12 cm and BC = 6 cm.
The angle B is :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Answer:
In $\Delta ABC$ AB = $6 \sqrt 3$ cm, AC = 12 cm and BC = 6 cm.
$AB^2+BC^2=108+36$
$=144$
$=12^2$
$=AC^2$
It satisfies the Pythagoras theorem.
Hence, ABC is a right-angled triangle and right-angled at B.
Option C is correct.
More About NCERT Solutions for Class 10 Maths Exercise 6.5
Most of the questions are based on right-angled triangles and the concept of similarity of triangles, but we should be also aware of some basic geometry which is used to solve problems of NCERT solutions for Class 10 Maths exercise 6.5. Pythagoras theorem is most important to solve questions of Class 10 Maths chapter 6 exercise 6.5. We should understand the properties of the trapezium and the criterion of similarity of triangles. Questions given in the exercise 6.5 Class 10 Maths are very much important for the board exam. Students can also access Triangles Class 10 Notes here and use them for quickly revision of the concepts related to Triangles.
Benefits of NCERT Solutions for Class 10 Maths Exercise 6.5
- Class 10 Maths chapter 6 exercise 6.5 is used to find the altitude of the triangle.
- NCERT Class 10 Maths chapter 6 exercise 6.5 is used to find the unknown side of a right-angle triangle.
- Exercise 6.5 Class 10 Maths, is founded on irrational numbers and the Fundamental Theorem of Arithmetic, both of which are key concepts in the chapter.
Also, See
NCERT Solutions of Class 10 Subject Wise
Frequently Asked Questions (FAQs)
The square of the length of the longest side of a right angle triangle is equal to the sum of the squares of the other two sides.
A rectangle's diagonal produces the same amount of area as its two sides combined (i.e., length and breadth).
Yes
By using Pythagoras theorem we can find that third side is 3cm
Yes, Pythagoras theorem is only valid for right angle triangles.
By using Pythagoras theorem, we can prove that the triangle is right angled.
When the square of one side of a triangle equals the sum of the squares of the other two sides, the angle opposite the first side is called a right angle.
Questions related to CBSE Class 10th
On Question asked by student community
HELLO,
I am attaching the link through which you can download and access the Bangalore Sahodaya Class 10th CBSE question paper of Mathematics ( Basic )
Here is the link :- https://school.careers360.com/download/ebooks/bangalore-sahodaya-class-10-mathematics-basic-question-paper-2025-26
It will help you to practice basic level numerical questions, strengthen fundamentals and prepare confidently for the board
HELLO,
Below i am attaching the direct link of Careers360 through which you can download the Bangalore Sahodaya Class 10th Mathematics Basic Question paper 2025 2026
Here is the link :- https://school.careers360.com/download/ebooks/bangalore-sahodaya-class-10-mathematics-basic-question-paper-2025-26
Hope this will help you!
Hello
You will be able to download the CBSE Class 10th Maths Sample Paper 2025-26 using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-10th-maths-sample-papers-2025-26
I hope this information helps you.
Thank you.
Hello,
Here you can access the last 5 years CBSE Class 10 Board Exam Question Papers from the mentioned link below:
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers-class-10
Hope it helps.
You can check the Class 11 English half yearly question paper and answer key for 2025 26 on the Careers360 website. These papers help students practice, understand the exam pattern, and check their answers for better preparation.
You can visit this Careers360 link to access the English question paper and
Popular CBSE Class 10th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
