• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 6.6 Class 10 Maths Chapter 6 - Triangles

NCERT Solutions for Exercise 6.6 Class 10 Maths Chapter 6 - Triangles

Edited By Ramraj Saini | Updated on Nov 25, 2023 08:29 PM IST | #CBSE Class 10th
Upcoming Event
CBSE Class 10th  Exam Date : 01 Jan' 2025 - 14 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.6

NCERT Solutions for Exercise 6.6 Class 10 Maths Chapter 6 Triangles are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 maths ex 6.6 help us to understand how to apply all the concepts till now we have learned through all the exercises in the chapter. The notion of triangle similarity, criteria for triangle similarity, areas of similar triangles, and Pythagoras Theorem are covered in this exercise.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.6
  2. More About NCERT Solutions for Class 10 Maths Exercise 6.6
  3. Benefits of NCERT Solutions for Class 10 Maths Exercise 6.6
  4. NCERT Solutions of Class 10 Subject Wise
  5. Subject Wise NCERT Exemplar Solutions

10th class Maths exercise 6.6 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Pearson | PTE

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

Apply

Triangles Class 10 Chapter 6 Exercise: 6.6

Q1 In Fig. 6.56, PS is the bisector of \angle QPR \: \: of\: \: \Delta PQR . Prove that \frac{QS }{SR } = \frac{PQ }{PR }

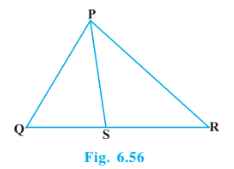
1635933619787

Answer:

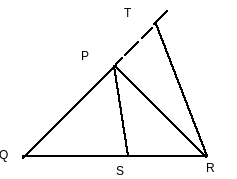
1635933634308

A line RT is drawn parallel to SP which intersect QP produced at T.

Given: PS is the bisector of \angle QPR \: \: of\: \: \Delta PQR .

\angle QPS=\angle SPR.....................................1

By construction,

\angle SPR=\angle PRT.....................................2 (as PS||TR)

\angle QPS=\angle QTR.....................................3 (as PS||TR)

From the above equations, we get

\angle PRT=\angle QTR

\therefore PT=PR

By construction, PS||TR

In \triangle QTR, by Thales theorem,

\frac{QS}{SR}=\frac{QP}{PT}

\frac{QS }{SR } = \frac{PQ }{PR }

Hence proved.

Q2(1) In Fig. 6.57, D is a point on hypotenuse AC of triangle ABC, such that BD \perp AC, DM \perp BC and DN \perp AB. Prove that : DM^2 = DN . MC

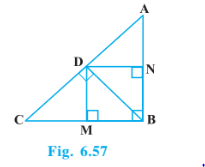
1635933650488

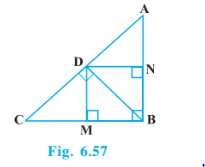
Answer:

1635933658497

Join BD

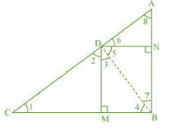
Given : D is a point on hypotenuse AC of D ABC, such that BD \perp AC, DM \perp BC and DN \perp AB.Also DN || BC, DM||NB

\angle CDB=90 \degree

\Rightarrow \angle 2+\angle 3=90 \degree.............................1

In \triangle CDM, \angle 1+\angle 2+\angle DMC=180 \degree

\angle 1+\angle 2=90 \degree.......................2

In \triangle DMB, \angle 3+\angle 4+\angle DMB=180 \degree

\angle 3+\angle 4=90 \degree.......................3

From equation 1 and 2, we get \angle 1=\angle 3

From equation 1 and 3, we get \angle 2=\angle 4

In \triangle DCM\, \, and\, \, \triangle BDM,

\angle 1=\angle 3

\angle 2=\angle 4

\triangle DCM\, \, \sim \, \, \triangle BDM, (By AA)

\Rightarrow \frac{BM}{DM}=\frac{DM}{MC}

\Rightarrow \frac{DN}{DM}=\frac{DM}{MC} (BM=DN)

\Rightarrow DM^2 = DN . MC

Hence proved

Q2 (2) In Fig. 6.57, D is a point on hypotenuse AC of D ABC, such that BD \perp AC, DM \perp BC and DN \perp AB. Prove that: DN^2 = DM . AN

1635933672815

Answer:

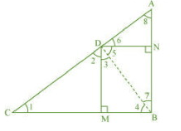
1635933684708

In \triangle DBN,

\angle 5+\angle 7=90 \degree.......................1

In \triangle DAN,

\angle 6+\angle 8=90 \degree.......................2

BD \perp AC, \therefore \angle ADB=90 \degree

\angle 5+\angle 6=90 \degree.......................3

From equation 1 and 3, we get \angle 6=\angle 7

From equation 2 and 3, we get \angle 5=\angle 8

In \triangle DNA\, \, and\, \, \triangle BND,

\angle 6=\angle 7

\angle 5=\angle 8

\triangle DNA\, \, \sim \, \, \triangle BND (By AA)

\Rightarrow \frac{AN}{DN}=\frac{DN}{NB}

\Rightarrow \frac{AN}{DN}=\frac{DN}{DM} (NB=DM)

\Rightarrow DN^2 = AN . DM

Hence proved.

Q3 In Fig. 6.58, ABC is a triangle in which \angle ABC > 90° and AD \perp CB produced. Prove that AC^2 = AB^2 + BC^2 + 2 BC . BD.

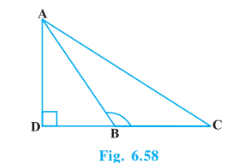
1635933712397

Answer:

In \triangle ADB, by Pythagoras theorem

AB^2=AD^2+DB^2.......................1

In \triangle ACD, by Pythagoras theorem

AC^2=AD^2+DC^2.......................2

AC^2=AD^2+(BD+BC)^2

\Rightarrow AC^2=AD^2+(BD)^2+(BC)^2+2.BD.BC

AC^2 = AB^2 + BC^2 + 2 BC . BD. (From 1)

Q4 In Fig. 6.59, ABC is a triangle in which \angle ABC < 90° and AD \perp BC. Prove that AC^2 = AB^2 + BC^2 - 2 BC . BD.

1635933729274

Answer:

In \triangle ADB, by Pythagoras theorem

AB^2=AD^2+DB^2

AD^2=AB^2-DB^2...........................1

In \triangle ACD, by Pythagoras theorem

AC^2=AD^2+DC^2

AC^2=AB^2-BD^2+DC^2 (From 1)

\Rightarrow AC^2=AB^2-BD^2+(BC-BD)^2

\Rightarrow AC^2=AB^2-BD^2+(BC)^2+(BD)^2-2.BD.BC

AC^2 = AB^2 + BC^2 - 2 BC . BD.

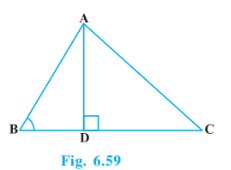
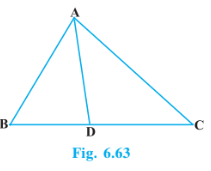
Q5 (1) In Fig. 6.60, AD is a median of a triangle ABC and AM \perp BC. Prove that : AC ^2 = AD ^2 + BC DM + \left ( \frac{BC}{2} \right ) ^2

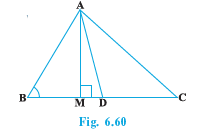
1635933758550

Answer:

Given: AD is a median of a triangle ABC and AM \perp BC.

In \triangle AMD, by Pythagoras theorem

AD^2=AM^2+MD^2.......................1

In \triangle AMC, by Pythagoras theorem

AC^2=AM^2+MC^2

AC^2=AM^2+(MD+DC)^2

\Rightarrow AC^2=AM^2+(MD)^2+(DC)^2+2.MD.DC

AC^2 = AD^2 + DC^2 + 2 DC . MD. (From 1)

AC^2 = AD^2 + (\frac{BC}{2})^2 + 2(\frac{BC}{2}). MD. (BC=2 DC)

AC ^2 = AD ^2 + BC DM + \left ( \frac{BC}{2} \right ) ^2

Q5 (2) In Fig. 6.60, AD is a median of a triangle ABC and AM \perp BC. Prove that : AB ^2 = AD ^2 - BC .DM + \left ( \frac{BC}{2} \right ) ^2

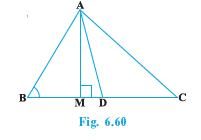
1635933791582

Answer:

In \triangle ABM, by Pythagoras theorem

AB^2=AM^2+MB^2

AB^2=(AD^2-DM^2)+MB^2

\Rightarrow AB^2=(AD^2-DM^2)+(BD-MD)^2

\Rightarrow AB^2=AD^2-DM^2+(BD)^2+(MD)^2-2.BD.MD

\Rightarrow AB^2=AD^2+(BD)^2-2.BD.MD

\Rightarrow AB^2 = AD^2 + (\frac{BC}{2})^2 -2(\frac{BC}{2}). MD.=AC^2 (BC=2 BD)

\Rightarrow AD^2 + (\frac{BC}{2})^2 -BC. MD.=AC^2

Q5 (3) In Fig. 6.60, AD is a median of a triangle ABC and AM \perp BC. Prove that: AC ^2 + AB ^2 = 2 AD^2 + \frac{1}{2} BC ^2

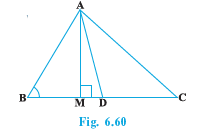
1635933807753

Answer:

In \triangle ABM, by Pythagoras theorem

AB^2=AM^2+MB^2.......................1

In \triangle AMC, by Pythagoras theorem

AC^2=AM^2+MC^2 ..................................2

Adding equation 1 and 2,

AB^2+AC^2=2AM^2+MB^2+MC^2

\Rightarrow AB^2+AC^2=2AM^2+(BD-DM)^2+(MD+DC)^2

\Rightarrow AB^2+AC^2=2AM^2+(BD)^2+(DM)^2-2.BD.DM+(MD)^2+(DC)^2+2.MD.DC

\Rightarrow AB^2+AC^2=2AM^2+2.(DM)^2+BD^2+(DC)^2+2.MD.(DC-BD) \Rightarrow AB^2+AC^2=2(AM^2+(DM)^2)+(\frac{BC}{2})^2+(\frac{BC}{2})^2+2.MD.(\frac{BC}{2}-\frac{BC}{2}) \Rightarrow AB^2+AC^2=2(AM^2+(DM)^2)+(\frac{BC}{2})^2+(\frac{BC}{2})^2

AC ^2 + AB ^2 = 2 AD^2 + \frac{1}{2} BC ^2

Q6 Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.

Answer:

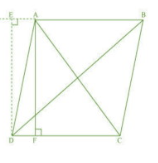
1635933824435

In parallelogram ABCD, AF and DE are altitudes drawn on DC and produced BA.

In \triangle DEA, by Pythagoras theorem

DA^2=DE^2+EA^2.......................1

In \triangle DEB, by Pythagoras theorem

DB^2=DE^2+EB^2

DB^2=DE^2+(EA+AB)^2

DB^2=DE^2+(EA)^2+(AB)^2+2.EA.AB

DB^2=DA^2+(AB)^2+2.EA.AB ....................................2

In \triangle ADF, by Pythagoras theorem

DA^2=AF^2+FD^2

In \triangle AFC, by Pythagoras theorem

AC^2=AF^2+FC^2=AF^2+(DC-FD)^2

\Rightarrow AC^2=AF^2+(DC)^2+(FD)^2-2.DC.FD

\Rightarrow AC^2=(AF^2+FD^2)+(DC)^2-2.DC.FD

\Rightarrow AC^2=AD^2+(DC)^2-2.DC.FD.......................3

Since ABCD is a parallelogram.

SO, AB=CD and BC=AD

In \triangle DEA\, and\, \triangle ADF,

\angle DEA=\angle AFD\, \, \, \, \, \, \, (each 90 \degree)

\angle DAE=\angle ADF (AE||DF)

AD=AD (common)

\triangle DEA\, \cong \, \triangle ADF, (ASA rule)

\Rightarrow EA=DF.......................6

Adding 2 and, we get

DA^2+AB^2+2.EA.AB+AD^2+DC^2-2.DC.FD=DB^2+AC^2 \Rightarrow DA^2+AB^2+AD^2+DC^2+2.EA.AB-2.DC.FD=DB^2+AC^2

\Rightarrow BC^2+AB^2+AD^2+2.EA.AB-2.AB.EA=DB^2+AC^2 (From 4 and 6)

\Rightarrow BC^2+AB^2+CD^2=DB^2+AC^2 \

Q7 (1) In Fig. 6.61, two chords AB and CD intersect each other at point P. Prove that : \Delta APC \sim \Delta DPB

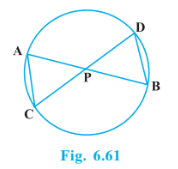
1635933839234

Answer:

1635933848323

Join BC

In \triangle APC\, \, and\, \triangle DPB,

\angle APC\, \, = \angle DPB ( vertically opposite angle)

\angle CAP\, \, = \angle BDP (Angles in the same segment)

\triangle APC\, \, \sim \triangle DPB (By AA)

Q7 (2) In Fig. 6.61, two chords AB and CD intersect each other at point P. Prove that : AP . PB = CP . DP

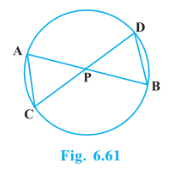
1635933860992

Answer:

1635933929931

Join BC

In \triangle APC\, \, and\, \triangle DPB,

\angle APC\, \, = \angle DPB ( vertically opposite angle)

\angle CAP\, \, = \angle BDP (Angles in the same segment)

\triangle APC\, \, \sim \triangle DPB (By AA)

\frac{AP}{DP}=\frac{PC}{PB}=\frac{CA}{BD} (Corresponding sides of similar triangles are proportional)

\Rightarrow \frac{AP}{DP}=\frac{PC}{PB}

\Rightarrow AP.PB=PC.DP

Q8 (1) In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that \Delta PAC \sim \Delta PDB

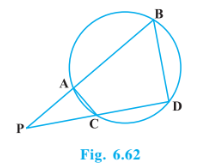
1635933941642

Answer:

In \Delta PAC \,and \,\Delta PDB,

\angle P=\angle P (Common)

\angle PAC=\angle PDB (Exterior angle of a cyclic quadrilateral is equal to opposite interior angle)

So, \Delta PAC \sim \Delta PDB ( By AA rule)

Q8 (2) In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that PA. PB = PC. PD

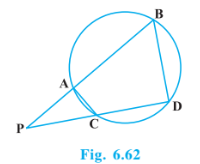
1635933976947

Answer:

In \Delta PAC \,and \,\Delta PDB,

\angle P=\angle P (Common)

\angle PAC=\angle PDB (Exterior angle of a cyclic quadrilateral is equal to opposite interior angle)

So, \Delta PAC \sim \Delta PDB ( By AA rule)

24440 \frac{AP}{DP}=\frac{PC}{PB}=\frac{CA}{BD} (Corresponding sides of similar triangles are proportional)

\Rightarrow \frac{AP}{DP}=\frac{PC}{PB}

\Rightarrow AP.PB=PC.DP

Q9 In Fig. 6.63, D is a point on side BC of D ABC such that \frac{BD }{CD} = \frac{AB}{AC} Prove that AD is the bisector of \angle BAC.

1635933987426

Answer:

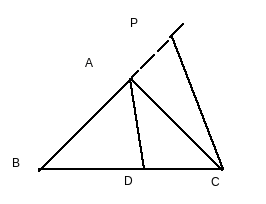
1635933998131

Produce BA to P, such that AP=AC and join P to C.

\frac{BD }{CD} = \frac{AB}{AC} (Given )

\Rightarrow \frac{BD }{CD} = \frac{AP}{AC}

Using converse of Thales theorem,

AD||PC \Rightarrow \angle BAD=\angle APC............1 (Corresponding angles)

\Rightarrow \angle DAC=\angle ACP............2 (Alternate angles)

By construction,

AP=AC

\Rightarrow \angle APC=\angle ACP............3

From equation 1,2,3, we get

\Rightarrow \angle BAD=\angle APC

Thus, AD bisects angle BAC.

Q10 Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. 6.64)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

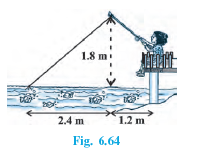
1635934015475

Answer:

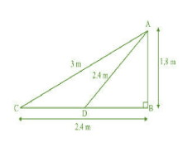
1635934024120

Let AB = 1.8 m

BC is a horizontal distance between fly to the tip of the rod.

Then, the length of the string is AC.

In \triangle ABC, using Pythagoras theorem

AC^2=AB^2+BC^2

\Rightarrow AC^2=(1.8)^2+(2.4)^2

\Rightarrow AC^2=3.24+5.76

\Rightarrow AC^2=9.00

\Rightarrow AC=3 m

Hence, the length of the string which is out is 3m.

If she pulls in the string at the rate of 5cm/s, then the distance travelled by fly in 12 seconds.

= 12\times 5=60cm=0.6m

Let D be the position of fly after 12 seconds.

Hence, AD is the length of the string that is out after 12 seconds.

Length of string pulled in by nazim=AD=AC-12

=3-0.6=2.4 m

In \triangle ADB,

AB^2+BD^2=AD^2

\Rightarrow (1.8)^2+BD^2=(2.4)^2

\Rightarrow BD^2=5.76-3.24=2.52 m^2

\Rightarrow BD=1.587 m

Horizontal distance travelled by fly = BD+1.2 m

=1.587+1.2=2.787 m

= 2.79 m

More About NCERT Solutions for Class 10 Maths Exercise 6.6

Class 10 Maths chapter 6 exercise 6: The questions in exercise 6.6 Class 10 Maths consist of many types of questions covering different types of theorems and formulas. Firstly we have a question in which we have to prove the left-hand side argument and right-hand side argument NCERT solutions for Class 10 Maths exercise 6.6 also have questions. Exercise 6.6 Class 10 Maths covers all types of questions that can be formed on the similarity of triangles. Students can also access Triangles Class 10 Notes here and use them for quickly revision of the concepts related to Triangles.

Benefits of NCERT Solutions for Class 10 Maths Exercise 6.6

  • Class 10 Maths chapter 6 exercise 6.6 broadly covers all kinds of questions that can be formed on the mixed concept of the triangle and gives a great amount of practice to conquer some amount of expertise in the triangle.
  • NCERT Class 10 Maths chapter 6 exercise 6.6, will be helpful in JEE Main (joint entrance exam) as triangles are a major part of some chapters.
  • Exercise 6.6 Class 10 Maths, is based on all the theorem, exercises and topics which have been covered in the whole chapter

Also, See:

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. What are the basic concepts covered till NCERT solutions Class 10 Maths chapter 6 exercise 6.6?

  • similarity of triangle

  • Criteria for Similarity of Triangles 

  • Areas of Similar Triangles

  • Pythagoras Theorem

2. What is the triangle's similarity?

If the respective angles are congruent and the corresponding sides are proportional, two triangles are said to be similar.

3. How are NCERT solutions for Class 10 Maths exercise 6.6 is different from other exercises ?

NCERT solutions for Class 10 Maths  exercise 6.6 is different from other exercises as all other exercises are based on a single concept and theorem they are base building exercises but Class 10 Maths chapter 6 exercise 6.6 is based on all the concepts.

4. Is NCERT solutions for Class 10 Maths exercise 6.6 difficult from other exercises?

Yes  Class 10 Maths chapter 6 exercise 6.6  because it have questions which have mix concepts 

5. How many theorems are there which we require to solve NCERT solutions for Class 10 Maths 1 exercise 6.6 ?

There are 13 main  theorems are there which we require to solve  NCERT solutions for Class 10 Maths 1 exercise 6.6

6. How many questions are there in the Exercise 6.6 Class 10 Maths ?

There are ten  questions in exercise 6.6 Class 10 Maths  question 

7. How many types of questions are there in the exercise 6.6 Class 10 Maths and explain each type?

There are two  types of questions in exercise 6.6 Class 10 Maths  question one type is there in which we have to proof LHS and RHS these contains uses of theorem and other is real life application of triangle    

Also Read

Articles

Upcoming School Exams

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

National Institute of Open Schooling 10th examination

Late Fee Application Date:21 December,2024 - 31 December,2024

National Institute of Open Schooling 12th Examination

Late Fee Application Date:21 December,2024 - 31 December,2024

All India Sainik Schools Entrance Examination

Application Date:24 December,2024 - 13 January,2025

Telangana Intermediate 1st Year Examination

Late Fee Application Date:25 December,2024 - 02 January,2025

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Digital Banking Business Model
 Via State Bank of India
Business Analytics Foundations
 Via PW Skills
Full-Stack Android Development
 Via Masai School
Introduction to Psychology
 Via San Jose State University, San Jose
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Board Exam Date 2025 Live: Bihar Class 10, 12 model papers out, time table soon; updates on CBSE, UP
December 06, 2024 - 10:42 PM IST
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST

Stay up-to date with CBSE Class 10th News

Back to top