NCERT Class 12 Physics Chapter 6 Notes, Electromagnetic Induction Class 12 Chapter 6 Notes

Ever wondered how electric current is generated without using a battery? That is exactly what you will explore in NCERT Notes Class 12 Physics Chapter 6: Electromagnetic Induction. This chapter helps you understand how magnetic fields and motion come together to produce electricity. These NCERT Notes is very important for students preparing for CBSE boards, JEE, or NEET, as it build strong fundamentals in electromagnetic induction and boost your problem-solving skills.

In these Electromagnetic Induction Class 12 Notes PDF, you will find clear explanations of Faraday’s laws, Lenz’s law, magnetic flux, inductance, mutual inductance and AC generator. These NCERT notes for class 12 include important formulas, important diagrams, and step-by-step solutions to a few previous year questions to make your revision smooth and effective. Whether you are revising for an exam or learning the topic for the first time.

New: CBSE 12 Class Free Mock Test

Latest:  JEE Main high scoring chapters | JEE Main 10 year's papers

Recommended: NEET high scoring chapters | NEET question papers with solutions

This Story also Contains

1. NCERT Notes for Class 12 Chapter 6: Download PDF
2. NCERT Notes for Class 12 Chapter 6
3. Electromagnetic Induction Previous year Question and Answer
4. NCERT Class 12 Notes Chapterwise

Also Read

• NCERT Solutions for Class 12 Physics Chapter 6 Electromagnetic Induction
• NCERT Exemplar Class 12 Physics Chapter 6 Solutions Electromagnetic Induction

NCERT Notes for Class 12 Chapter 6: Download PDF

Revise anytime and without internet using the PDF version of the NCERT Notes of Electromagnetic Induction. Download it using the button below and save it for later study.

Download PDF

NCERT Notes for Class 12 Chapter 6

The NCERT Notes of Electromagnetic Induction are prepared according to the latest NCERT syllabus. They explain all the topics in simple and easy-to-understand language, and are useful for additional learning.

The experiments of Faraday and Henry

Faraday performed various experiments to discover and understand the phenomenon of electromagnetic induction. Some of them are :

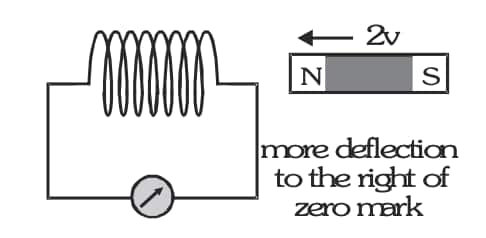
• When the magnet is held stationary anywhere near or inside the coil, the galvanometer does not show any deflection.
  

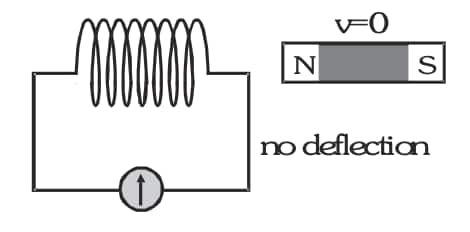
• When the N-pole of a strong bar magnet is moved towards the coil, the galvanometer shows a deflection right to the zero mark.
  

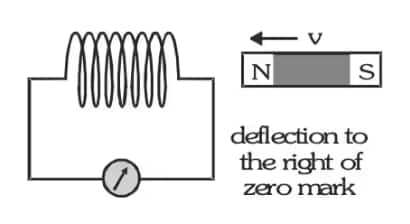
• When the N-pole of a strong bar magnet is moved away from the coil, the galvanometer shows a deflection left to the zero mark.
  

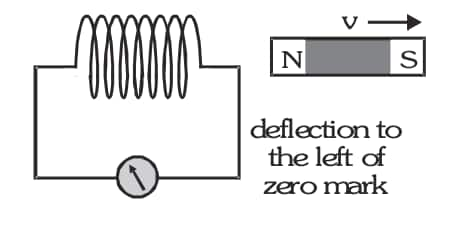
• If the above experiments are repeated by bringing the S-pole of the, magnet towards or away from the coil, the direction of current in the coil is opposite to that obtained in the case of N-pole.
  

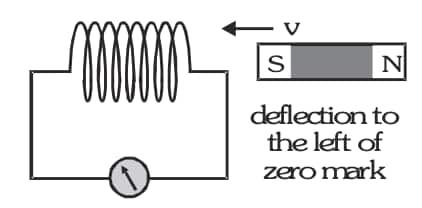
• The deflection in galvanometer is more when the magnet moves faster and less when the magnet moves slow.
  

Magnetic Flux

The magnetic flux $(\varphi )$ linked with a surface held in a magnetic field $(\mathrm{B})$ is defined as the number of magnetic lines of force crossing that area (A). If $\theta$ is the angle between the direction of the field and normal to the area, (area vector) then $\varphi =\overrightarrow{B}\cdot \overrightarrow{A}=BA\cos \theta$

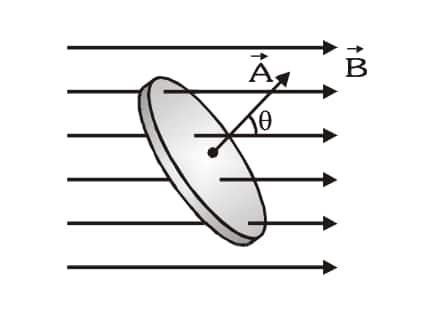
Note down the following points regarding the magnetic flux :
(i) Magnetic flux is a scalar quantity (dot product of two vector quantities is a scalar quantity)
(ii) The SI unit of magnetic flux is tesla-metre ${}^2(1\mathrm{T}-{\mathrm{m}}^2)$. This unit is called weber $(1\mathrm{Wb})$.

$1\mathrm{Wb}=1\mathrm{T}-{\mathrm{m}}^2=1\mathrm{N}-\mathrm{m}/\mathrm{A}$

Thus, unit of magnetic field is also weber $/{\mathrm{m}}^2\left(1\mathrm{Wb}/{\mathrm{m}}^2\right)$.
or

$1\mathrm{T}=1\mathrm{Wb}/{\mathrm{m}}^2$

• For a given area flux will be maximum :
  when magnetic field $\overrightarrow{B}$ is normal to the area
  $\theta =0\Rightarrow \cos \theta =\text{ maximum }=1$
  ${\varphi }_{max}=\mathrm{B}\mathrm{A}$
• For a given area flux will be minimum :
  when magnetic field $\overrightarrow{B}$ is parallel to the area $\theta =90\Rightarrow \cos \theta =\text{ minimum }=0$
  ${\varphi }_{min}=0$

Faraday’s Law of Induction

Based on his experimental studies on the phenomenon of electromagnetic induction, Faraday proposed the following two laws.

First law
Whenever the amount of magnetic flux linked with a closed circuit changes, an emf is induced in the circuit. The induced emf lasts so long as the change in magnetic flux continues.

Second law
The magnitude of emf induced in a closed circuit is directly proportional to rate of change of magnetic flux linked with the circuit. If the change in magnetic flux in a time dt is $=\mathrm{d}\varphi$ then $e\propto \frac{\mathrm{d}\varphi }{\mathrm{dt}}$

Lenz's Law and Conservation of Energy

The negative sign in Faraday's equations of electromagnetic induction describes the direction in which the induced emf drives current around a circuit. However, that direction is most easily determined with the help of Lenz's law. This law states that:
"The direction of any magnetic induction effect is such as to oppose the cause of the effect."

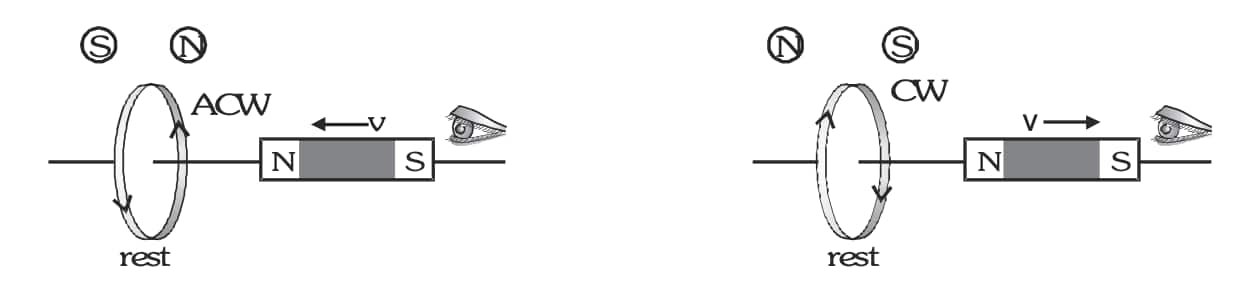
This law is a direct consequence of the principle of conservation of energy. It ensures that energy is not created or destroyed in the process of electromagnetic induction.

Motional Electromotive Force

Let us consider a straight conductor moving in a uniform and time independent magnetic field.

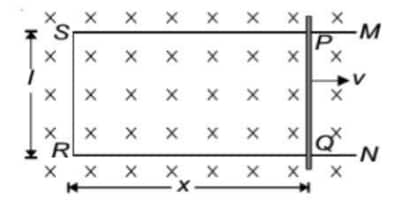
Figure shows a rectangular conductor MSRN upon which a conducting rod PQ moves (without friction) with constant velocity $\overrightarrow{v}$. The magnetic field $\overrightarrow{B}$ is perpendicular (inward) to the plane of closed conducting loop $PSRQ$.
The magnetic flux enclosed by the loop at $t=t\mathrm{s}$.

${\varphi }_{B(t)}=\overrightarrow{B}\cdot \overrightarrow{A}=BA=BA=BIx(t)$

The rate of change of this magnetic flux will induce an emf given by $e=-\frac{d}{dt}{\varphi }_B=-\frac{d}{dt}(-B\ell x(t))$
$e=B\ell \cdot \frac{dx(t)}{dt}$
$e=B\ell v$
This emf, which is obtained due to the motion of conductor instead of changing the magnetic field, is known as motional emf.

Inductance

Self-Inductance: When the current through the coil changes, the magnetic flux linked with the coil also changes. Due to this change of flux a current induced in the coil itself according to lenz concept it opposes the change in magnetic flux. This phenomenon is called self-induction and a factor by virtue of coil shows opposition for change in magnetic flux called cofficient of self-inductance of coil.

Case - I Current through the coil is constant
If I $\to \mathrm{B}\to \varphi$ (constant) $\Rightarrow$ No EMI

total flux of coil $(N\varphi )\propto$ current through the coil
$\mathrm{N}\varphi \propto \mathrm{I}$
$\mathrm{N}\varphi =\mathrm{LI}$
$\mathrm{L}=\frac{\mathrm{N}\varphi }{\mathrm{I}}$

where $L=$ coefficient of self inductance of coil

Case - II Current through the coil changes w.r.t. time

$\begin{array}{rl}& \text{ If }\mathrm{N}\varphi =\mathrm{LI}\\ & -\mathrm{N}\frac{\mathrm{d}\varphi }{\mathrm{dt}}=-\mathrm{L}\frac{\mathrm{dI}}{\mathrm{dt}},(-\mathrm{N}\frac{\mathrm{d}\varphi }{\mathrm{dt}})\text{ called total self induced emf of coil ' }{e}_{\mathrm{s}}^{\prime }\\ & e_{\mathrm{s}}=-\mathrm{L}\frac{\mathrm{dI}}{\mathrm{dt}}\end{array}$

Self-Inductance of a Solenoid
Let cross-sectional area of solenoid=A, Current flowing through it=I
Length of the solenoid $=\ell ,$

then $\varphi =NBA=N\frac{{\mu }_{0}NIA}{\ell }=\frac{{\mu }_0{N}^{2}AI}{\ell }$
But $\varphi =\mathrm{LI}$
$\therefore \mathrm{L}=\frac{{\mu }_0{\mathrm{N}}^2\mathrm{A}}{\ell }$
If no iron or similar material is nearby, then the value of self-inductance depends only on the geometrical factors (length, cross-sectional area, number of turns).

Mutual Induction

Whenever the current passing through the primary coil or circuit change then magnetic flux neighbouring secondary coil or circuit will also change. According to Lenz for the opposition of flux change so an emf induced in the neighbouring coil or circuit. This phenomenon called as 'Mutual induction'. In case of mutual inductance for two coils situated close to each

other, flux linked with the secondary due to the current in the primary.

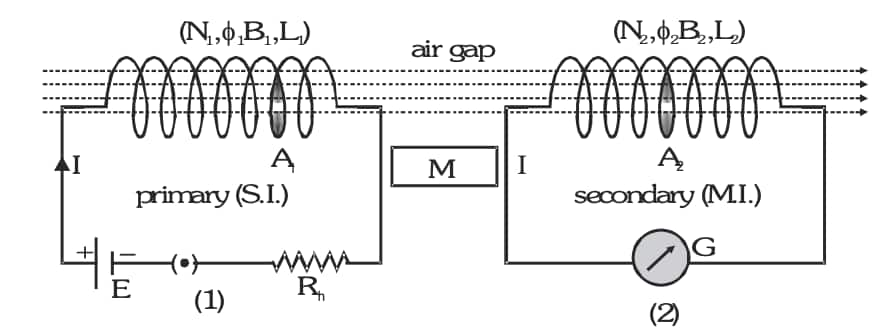
Case - I: When current through the primary is constant

Total flux of secondary is directly proportional to current flow through the primary coil.

${\mathrm{N}}_2{\varphi }_2\propto {\mathrm{I}}_1$
${\mathrm{N}}_2{\varphi }_2={\mathrm{MI}}_1,$
$\mathrm{M}=\frac{{\mathrm{N}}_2{\varphi }_2}{{\mathrm{I}}_1}$

where M : is coefficient of mutual induction.

Case - II When current through primary changes with respect to time

${\mathrm{N}}_2{\varphi }_2={\mathrm{MI}}_1$
$-{\mathrm{N}}_2\frac{\mathrm{d}{\varphi }_2}{\mathrm{dt}}=-\mathrm{M}\frac{{\mathrm{dI}}_1}{\mathrm{dt}}$

$e_{\mathrm{m}}=-\mathrm{M}\left(\frac{\mathrm{d}{\mathrm{I}}_1}{\mathrm{dt}}\right)$

where M : is coefficient of mutual induction.

Coefficient of coupling (K):

The coefficient of coupling of two coils is defined as $K=\frac{M}{\sqrt{L_1{L}_2}}$

Energy stored in an inductor: The energy stored in an inductor is given by when a current I flows through it.

$\mathbf{U}=\frac{1}{2}\mathbf{L}{\mathbf{I}}^{\mathbf{2}}$

Magnetic energy is the form of energy stored in an inductor.

AC Generator

• An electrical generator turns mechanical energy into electrical energy.

• The phenomenon of electromagnetic induction is used to generate alternating currents (ac).

• An emf is induced in the coil whenever the magnetic flux changes.

• A device that converts mechanical energy into electrical energy is known as an AC generator (alternating currents).

• By altering the magnetic field and area vector, an AC generator can induce an emf or current in a loop.

Principle:-

• A change in the loop's orientation or effective area causes current to flow through it.

• Modifying the area vector or changing the induced emf produces induced emf.

• Fleming's right-hand rule determines the direction of the current.

• The up and down movement of the loops changes the direction of the current in the circuit.

It based on The phenomenon of electromagnetic induction asserts that whenever the magnetic flux associated with a conductor (or coil) changes, an emf is induced in the coil.

If E is the induced emf in the coil, then

$\begin{array}{rl}& E=NBA\omega \sin \omega t\\ & E=E_0\sin \omega t\end{array}$

E₀=NBAω is the induced EMF's maximum or peak value.

Electromagnetic Induction Previous year Question and Answer

Q1: The self-inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as

(A) l and A increase.
(B) l decreases and A increases.
(C) l increases and A decreases.
(D) both l and A decrease.

Answer:

The formula for self-inductance of a solenoid is given by:

$L=\frac{\left({\mu }_r{\mu }_0{n}^2\right)}{I}$
So, from the equation, the inductance should increase as I decrease and $A$ increases. As $L$ is inversely proportional to I and directly proportional to A.

Hence, the answer is the option (B).

Q2. The number of turns of a solenoid is doubled without changing its length and area of cross-section. The self-inductance of the solenoid will become ___________ times.
(A)4
(B) 2
(C) 6
(D) 3

Answer :

$L=\frac{{\mu }_0{N}^{2}A}{l}$
The area and length are not changed. Therefore

$L\propto N^2$
Therefore when the number of turns of a solenoid are doubled the inductance will become 4 times.

Hence, the answer is the option (1).

Q3: Define the self-inductance of a coil. Obtain the expression for the energy stored in an inductor L connected across a source of emf.

Answer :

Self-induction: Induction of emf in a coil due to a change in current in the same coil.

$N\varphi \propto I$

$\therefore N\varphi =LI$

Where L is known as the coefficient of self-induction or self-inductance.

Consider an inductor connected across an emf E. For current $(\mathrm{I})$ at an instant in the circuit

$\begin{array}{rl}& \frac{dW}{dt}=EI\\ & =\frac{LdI}{dt}\times I\\ & dW=LIdI\end{array}$

The amount of work done in establishing the current I is

$\begin{array}{rl}W& =\int dW={\int }_0^{I}LIdI\\ & =\frac{1}{2}L{I}^2=\text{ energy stored }\end{array}$

NCERT Class 12 Notes Chapterwise

Subject Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 12 Solutions

• NCERT Exemplar Class 12 Maths

• NCERT Exemplar Class 12 Physics

• NCERT Exemplar Class 12 Chemistry

• NCERT Exemplar Class 12 Biology

Subject Wise NCERT Solutions

• NCERT Solutions for Class 12 Mathematics

• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for Class 12 Physics

• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus