Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 6.3 Class 9 Maths Chapter 6 - Lines and Angles

NCERT Solutions for Exercise 6.3 Class 9 Maths Chapter 6 - Lines and Angles

Edited By Vishal kumar | Updated on Oct 06, 2023 09:22 AM IST

NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles Ex 6.3- Download Free PDF

NCERT Solutions Class 9 Maths Chapter 6 Exercise 6.3 Lines and Angles- We'll explore the creation of lines and angles in 9th class maths exercise 6.3 answers of NCERT Solutions. This chapter explains how lines and angles interact and teaches us key rules and theorems. We may improve our problem-solving skills and see how lines and angles are utilised in maths and in the real world by undertaking the tasks in this chapter.

This Story also Contains
  1. NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles Ex 6.3- Download Free PDF
  2. NCERT Solutions Class 9 Maths Chapter 6 Exercise 6.3 Lines and Angles
  3. More About NCERT Solutions for Class 9 Maths Exercise 6.3
  4. Benefits of NCERT Solutions for Class 9 Maths Exercise 6.3
  5. Key Features of Class 9 Maths Chapter 6 Exercise 6.3
  6. NCERT Solutions of Class 10 Subject Wise
  7. Subject Wise NCERT Exemplar Solutions

The class 9 maths chapter 6 exercise 6.3 have been carefully crafted by subject experts using simple language and clear explanations. There are a total of six questions that cover important concepts related to lines and angles. Additionally, students have the option to download the PDF version of these exercise 6.3 class 9 mathssolution for offline use, all without any cost. These resources are designed to make learning easier and more accessible for students, Along with NCERT book Class 9 Maths, chapter 6 exercise 6.3 the following exercises are also present.

NCERT Solutions Class 9 Maths Chapter 6 Exercise 6.3 Lines and Angles

Download PDF


Access Lines and Angles Class 9 Maths Chapter 6 Exercise: 6.3

Q1 In Fig. 6.39, sides QP and RQ of \Delta PQR are produced to points S and T respectively. If \angle SPR = 135° and \angle PQT = 110°, find \angle PRQ.

1640150386912

Answer:

15956110080781595611005967
Given,
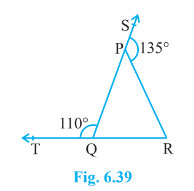
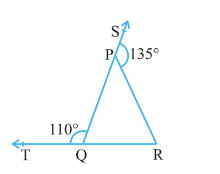
PQR is a triangle, \angle SPR = 135^0 , \angle PQT = 110^0

Now, \angle TQP + \angle PQR = 180^0 (Linear pair)
So, \angle PQR = 180^0-110^0 = 70^0

Since the side of QP of the triangle, PQR is produced to S
So, \angle PQR + \angle PRQ = 135^0 (Exterior angle property of triangle)
\therefore \angle PRQ = 135^0 - 70^0 = 65^0

Q2 In Fig. 6.40, \angle X = 62°, \angle XYZ = 54°. If YO and ZO are the bisectors of \angle XYZ and \angle XZY respectively of \Delta XYZ, find \angle OZY and \angle YOZ.

15956111030681595611095537
Answer:

We have
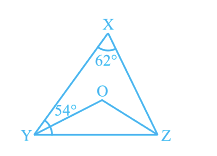
\angle X = 62^0 , \angle XYZ = 54^0
YO and ZO bisects the \angle XYZ and \angle XZY
Now, In \Delta XYZ, by using angle sum property
\angle XYZ + \angle YZX + \angle ZXY = 180^0

So, \angle YZX = 180^0-54^0-62^0
\angle YZX = 64^0

and, \angle OYZ = 54^0/2 = 27^0 also, \angle OZY = 32^0

Now, in \Delta OYZ
\angle Y + \angle O + \angle Z = 180^0 [ \angle Y = 32^0 and \angle Z = 64^0 ]
So, \angle YOZ = 121^0

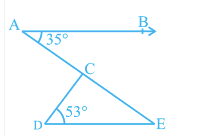
Q3 In Fig. 6.41, if AB || DE, \angle BAC = 35° and \angle CDE = 53°, find \angle DCE.

15956111843421595611181275
Answer:

We have,
AB || DE, \angle BAC = 35° and \angle CDE = 53°

AE is a transversal so, \angle BAC = \angle AED = 35^0

Now, In \Delta CDE,
\angle CDE + \angle DEC + \angle ECD = 180^0 (By angle sum property)
Therefore, \angle ECD = 180^0-53^0-35^0
\angle ECD = 92^0

Q4 In Fig. 6.42, if lines PQ and RS intersect at point T, such that \angle PRT = 40°, \angle RPT = 95° and \angle TSQ = 75°, find \angle SQT.

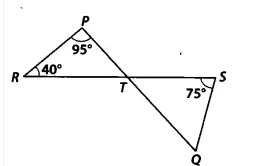
15956112332891595611230995
Answer:

We have,
lines PQ and RS intersect at point T, such that \angle PRT = 40°, \angle RPT = 95° and \angle TSQ = 75°

In \Delta PRT, by using angle sum property
\angle PRT + \angle PTR + \angle TPR = 180^0
So, \angle PTR = 180^0 -95^0-40^0
\Rightarrow \angle PTR = 45^0

Since lines, PQ and RS intersect at point T
therefore, \angle PTR = \angle QTS (Vertically opposite angles)
\angle QTS = 45^0

Now, in \Delta QTS,
By using angle sum property
\angle TSQ + \angle STQ + \angle SQT = 180^0
So, \angle SQT = 180^0-45^0-75^0
\therefore \angle SQT = 60^0

Q5 In Fig. 6.43, if PQ \bot PS, PQ || SR, \angle SQR = 28° and \angle QRT = 65°, then find the values of x and y .

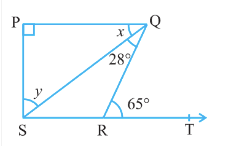
15956112915331595611289597
Answer:

We have,
PQ \bot PS, PQ || SR, \angle SQR = 28° and \angle QRT = 65°
Now, In \Delta QRS, the side SR produced to T and PQ || RS
therefore, \angle QRT = 28^0+x = 65^0
So, x = 37^0

Also, \angle QRT = \angle RSQ + \angle SQR (By exterior angle property of a triangle)
Therefore, \angle RSQ = \angle QRT - \angle SQR
\angle RSQ = 65^0-28^0 = 37^0

Now, in \Delta PQS,
\angle P + \angle PQS + \angle PSQ = 180^0
y=180^0-90^0-37^0
y=52^0

Q6 In Fig. 6.44, the side QR of \Delta PQR is produced to a point S. If the bisectors of \angle PQR and \angle PRS meet at point T, then prove that \angle QTR = \frac{1}{2} \angle QPR.

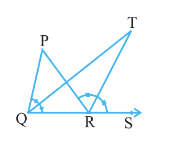
15956113451601595611343477
Answer:

We have,
\Delta PQR is produced to a point S and bisectors of \angle PQR and \angle PRS meet at point T,
By exterior angle sum property,
\angle PRS = \angle P + \angle PQR
Now, \frac{1}{2}\angle PRS =\frac{1}{2}\angle P + \frac{1}{2} \angle PQR
\Rightarrow \angle TRS = \frac{1}{2}\angle P + \angle TQR ................(i)

Since QT and QR are the bisectors of \angle PQR and \angle PRS respectively.

Now, in \Delta QRT,
\angle TRS = \angle T + \angle TQR ..............(ii)

From eq (i) and eq (ii), we get

\frac{1}{2}\angle P= \angle T
\Rightarrow \frac{1}{2}\angle QPR= \angle QTR
Hence proved.

The angle sum property in triangles is proved using the theorems and axioms of parallel lines in NCERT Solutions for Class 9 Maths chapter 6 exercise 6.3 Lines and Angles. The triangle angle sum property states that the sum of a triangle's angles is 180 degrees.

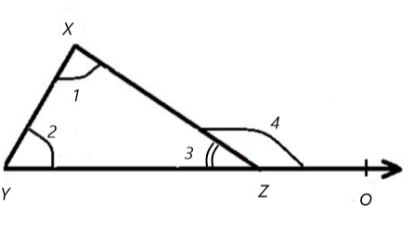
lines%20angles6

If a triangle side is formed, the exterior angle formed is equal to the sum of the two interior opposite angles. i.e. An exterior angle of a triangle = sum of opposite internal angles.

We can also prove this theorem very easily just by equating two equations.

We know that the sum of all interior angles of triangles is 180. So, from the above figure.

1640155572911 (1)

And we also know that the angle of a straight line is 180.

1640155573063 (2)

We will now equate equations 1 and 2 because the right-hand side of both equations is 180.

Hence,

1640155572306

We subtract angle 3 from both sides. So,

1640155573271

Hence, the exterior angle is equal to the sum of two opposite interior angles.

If a triangle side is formed, the exterior angle formed is equal to the sum of the two interior opposite angles.

More About NCERT Solutions for Class 9 Maths Exercise 6.3

Intersecting lines are lines that cross each other from a specific point. Non-intersecting Lines are lines that never cross each other at any point. These are known as Parallel Lines, and the distance between parallel lines is the common length between two lines.

When a line passes through two distinct lines and intersects them at different points, this line is referred to as a transversal line.

Complementary angles are those whose sum of two angles equals 90°.

Supplementary angles are those whose sum of two angles equals 180°.

Also Read| Lines And Angles Class 9 Notes

Benefits of NCERT Solutions for Class 9 Maths Exercise 6.3

  • From NCERT syllabus Class 9 Maths chapter 6 exercise 6.3 we learn new formulas to calculate the mean and class mark.
  • Exercise 6.3 Class 9 Maths, is based on the angle sum property of a triangle
  • Understanding the concepts from Class 9 Maths chapter 6 exercise 6.3 will allow us to understand the concepts related to higher standard questions related to angle sum property of a triangle

Key Features of Class 9 Maths Chapter 6 Exercise 6.3

  1. Comprehensive Coverage: The exercise 6.3 class 9 maths covers various concepts related to lines and angles, ensuring a thorough understanding of this fundamental geometry topic.

  2. Expert-Crafted Solutions: The class 9 maths ex 6.3 solutions provided are written by subject experts, offering clear and concise explanations to help students grasp the concepts easily.

  3. Easy-to-Understand Language: The 9th class maths exercise 6.3 answers are presented in simple and easy-to-understand language, making it accessible to students of all levels.

  4. Variety of Questions: The class 9 ex 6.3 consists of a total of six questions, offering a variety of problem types to test students' understanding and problem-solving skills.

  5. Conceptual Clarity: By solving these ex 6.3 class 9 questions, students can gain a deeper understanding of the relationships between lines and angles, helping them build a strong foundation in geometry.

  6. Offline Accessibility: Students have the option to download the PDF version of the solutions, allowing them to access and use the resources offline without any additional cost.

Also, See

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. What is the main concept of Class 9 Maths chapter 6 exercise 6.3?

This exercise is about the Angle Sum Property of a triangle, types of angles like vertically opposite angles and axioms.

2. Define a triangle?

A triangle is a closed geometric object with three sides and three angles that has three sides and three angles.

3. What is the total of a triangle's angles?

The sum of a triangle's angles is 180.

4. What is the outer angle of a triangle?

The sum of a triangle's two inner opposite angles equals the triangle's outer angle.

5. Two angles of a triangle are 120° and 20° find the third angle?

Since the sum of all the angles of a triangle is 180

And the rest two angles are 120 and 20

The third angle is 180-140=40 

6. Can we make a triangle with two angles of 110° and 90°?

No, we can’t make a triangle with two angles as 110° and 90°. Because the sum exceeds 180

7. The angles of a triangle are in the ration of 1:4:7, find all the angles of the triangle?

The angles are 15°, 60° and 105°

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Karnataka Pre-University Certificate Examination

Exam Date:03 May,2024 - 03 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
Barmer teacher suspended for slapping class 3 student
01/05/2024, 17:07:10
Teacher arrested for `sexual exploitation' at Ujjain Ashram school
01/05/2024, 14:28:18
Delhi NCR schools get bomb threat; fire tender arrives, search underway
01/05/2024, 04:09:04
Education is greatest gift to society: Vice President Jagdeep Dhankhar
30/04/2024, 17:02:12
Jharkhand schools up to Class 8 closed till further orders due to heat wave
30/04/2024, 11:49:37
Delhi School EWS Admission 2024-25: Registration window opens at edudel.nic.in; eligibility
30/04/2024, 09:27:25
Education ministry asks NCERT to review, update textbooks on yearly basis
29/04/2024, 12:22:03
Back to top