NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.2

Team Careers360Updated on 21 May 2025, 03:28 PM IST

Parallel lines are lines that are equidistant from each other. Parallel lines never intersect or meet each other at any point. A transversal line intersects two or more lines at distinct points. As shown in the figure, line l crosses lines m and n at P and Q, respectively. Line l is thus a transversal for lines m and n.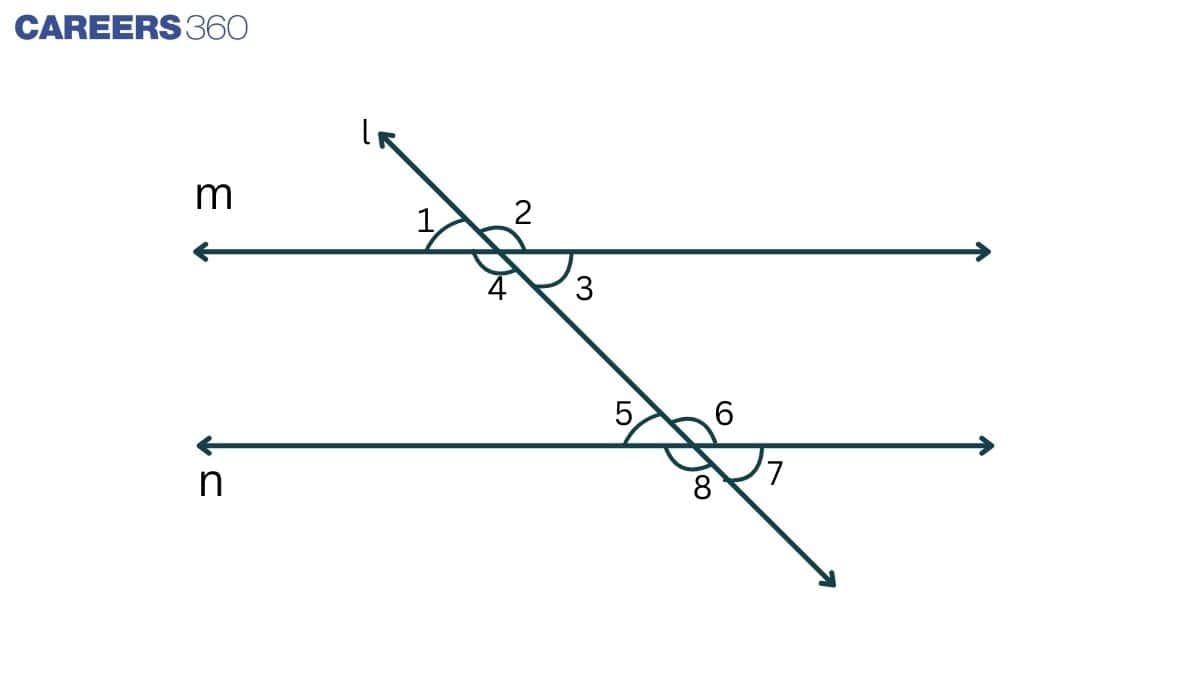

1745305371936

This Story also Contains

Access Lines and Angles Class 9 Maths Chapter 6 Exercise: 6.2
Topics covered in Chapter 6, Lines and Angles: Exercise 6.2
NCERT Solutions of Class 9 Subject Wise
Subject-Wise NCERT Exemplar Solutions

In this figure,

∠1=∠5, ∠2=∠6, ∠4=∠8 and ∠3=∠7(Corresponding angles)
∠3=∠5, ∠4=∠6 (Alternate interior angles)
∠1=∠7, ∠2=∠8 (Alternate exterior angles)

Consecutive interior angles, also known as associated angles or co-interior angles, are interior angles on the same side of the transversal. The corresponding angles are identical when a transversal connects two parallel lines. The two lines are parallel if a transversal intersects them so that a pair of corresponding angles are equal.

NCERT Solutions Class 9 Maths exercise 6.2 – this exercise includes some very important theorems from the examination point of view. So, the theorems and their proof given in the NCERT Books are:

When a transversal intersects two parallel lines, each pair of alternate interior angles is equal.
The lines are parallel if a transversal intersects two lines in such a way that their inner angles are equal.
If a transversal overlaps two parallel lines, each pair of internal angles on the same side is supplementary.

Access Lines and Angles Class 9 Maths Chapter 6 Exercise: 6.2

Q1. In Fig. 6.23, if AB $||$ CD, CD $||$ EF and y : z = 3 : 7 , find x .

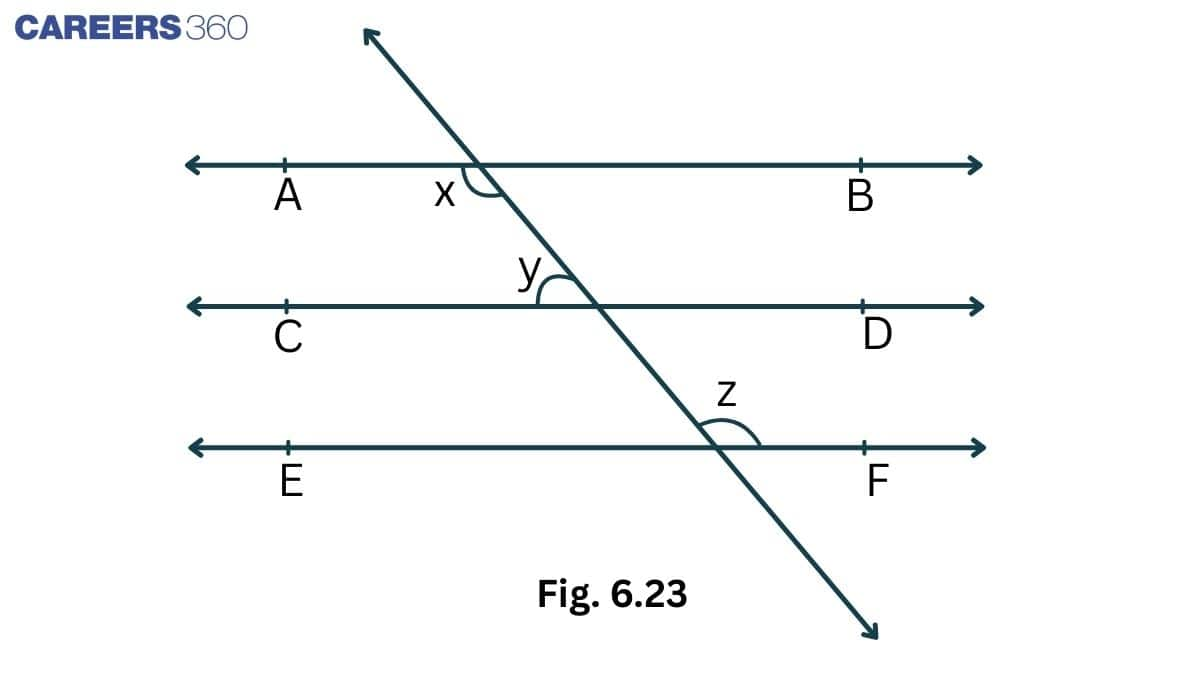
1745305506995

Solution:
Given that,
AB || CD and CD || EF and $y:z = 3:7 \Rightarrow z = \frac{7}{3}y$
Therefore, AB || EF and $x =z$ (Alternate interior angles)..............(i)
Again, CD || AB
As the angles on the same side of a transversal sum is 180°
$\\\Rightarrow x+y =180^0$
$\\ \Rightarrow z+y =180^0$ .............(ii)
Putting the value of $z$ in equation (ii), we get
$\frac{10}{3}y =180^0 $
$\Rightarrow y =54^0$
Then $z=180^0-54^0=126^0$
By equation (i), we get the value of $x=126^0$

Q2. In Fig. 6.24, if AB $||$ CD, EF $\bot$ CD and $\angle$ GED = 126°, find $\angle$ AGE, $\angle$ GEF and $\angle$ FGE.

Solution: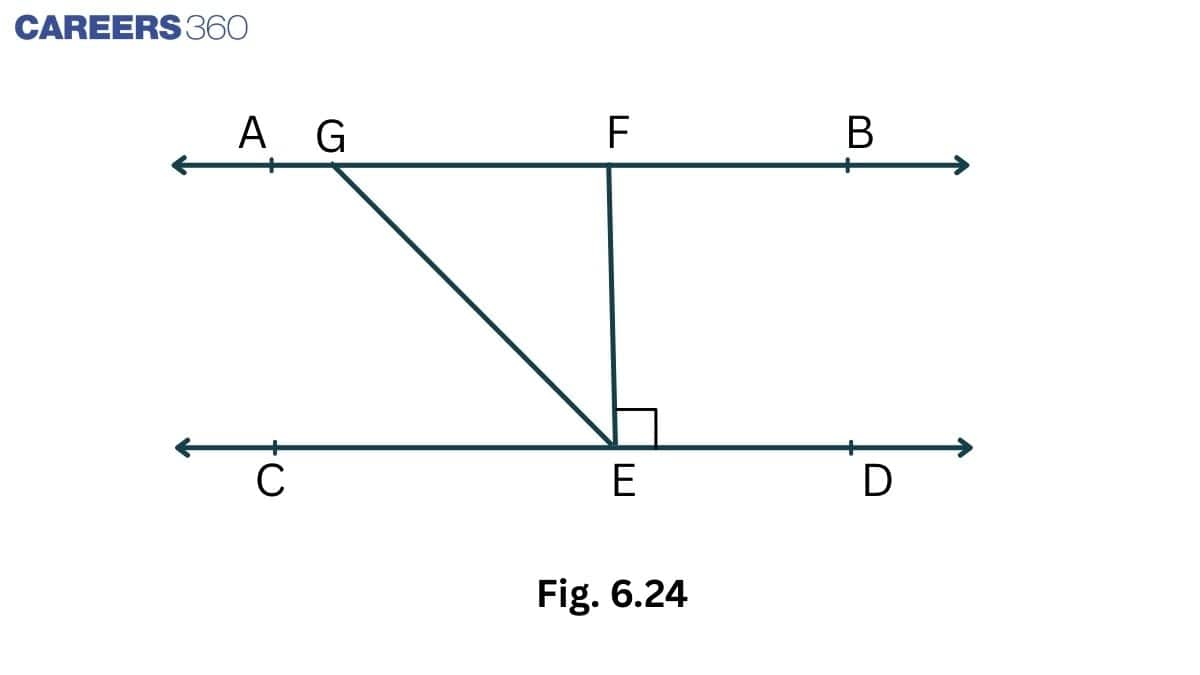
1745305548547
Given,
AB || CD, EF $\perp$ CD and $\angle$ GED = $126^0$
In the above figure,
GE is transversal. So, that $\angle$ AGE = $\angle$ GED = $126^0$ [Alternate interior angles]
Also, $\angle$ GEF = $\angle$ GED - $\angle$ FED
$\angle$ GEF = $126^0-90^0 = 36^0$
$\angle GEF = 36^0$
Since AB is a straight line
Therefore, $\angle$ AGE + $\angle$ FGE = $180^0$
So, $\angle$ FGE = $180^0-\angle AGE
$\angle$ FGE = 180^0 - 126^0$
$\Rightarrow \angle FGE =54^0$

Q3. In Fig. 6.25, if PQ $||$ ST, $\angle$ PQR = 110° and $\angle$ RST = 130°, find $\angle$ QRS. [ Hint : Draw a line parallel to ST through point R.]

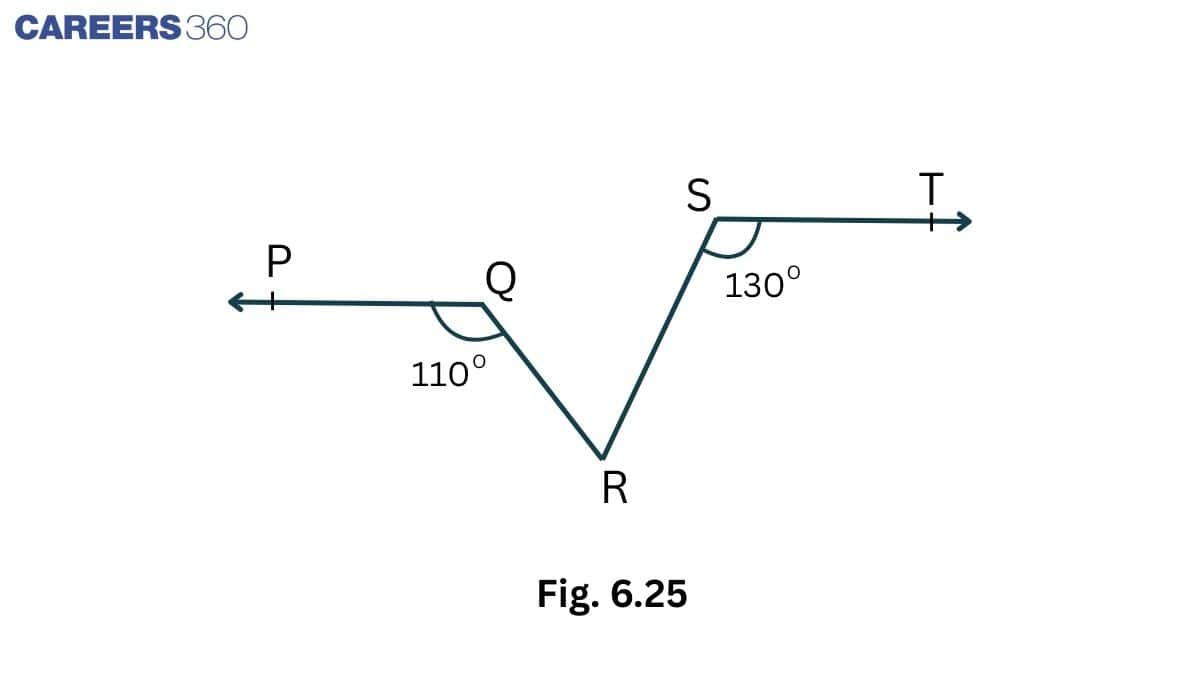
1745305650123

Solution:

Draw a line EF parallel to the ST through R.
Since PQ || ST and ST || EF
$\Rightarrow$ EF || PQ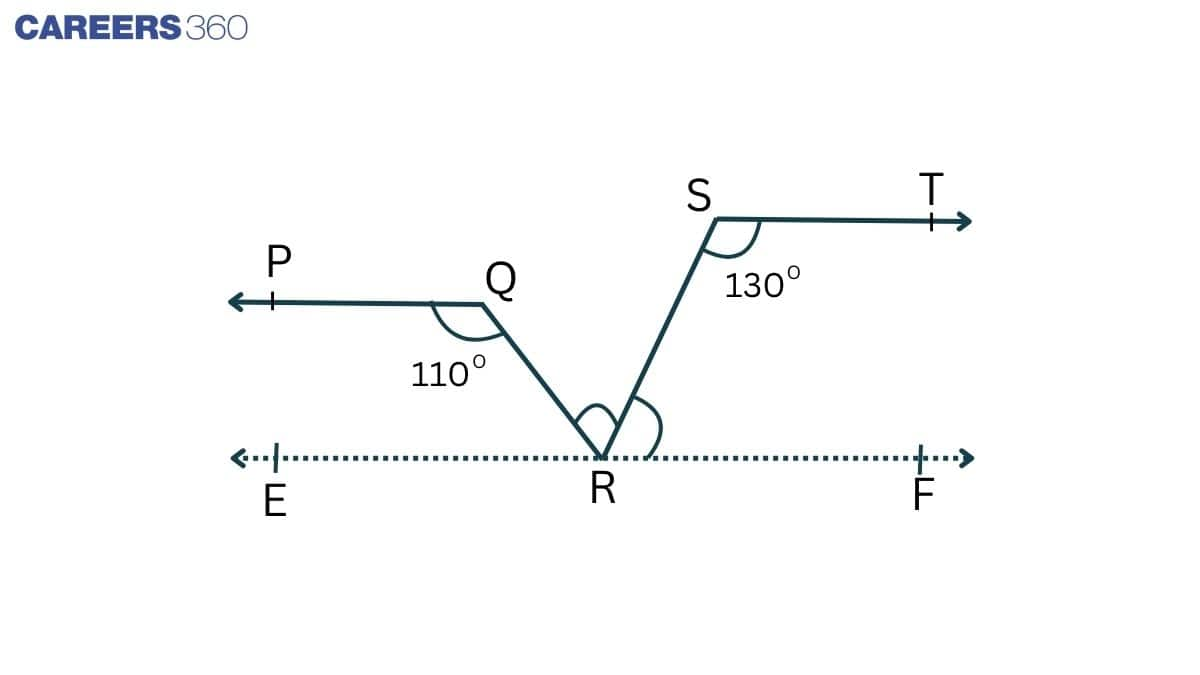

1745305650515

$\angle$ PQR = $\angle$ QRF = $110^0$ (Alternate interior angles)$\angle$ QRF = $\angle$ QRS + $\angle$ SRF .............(i)
Again, $\angle$ RST + $\angle$ SRF = $180^0$ (Interior angles of two parallels ST and RF)
$\Rightarrow \angle SRF =180^0-130^0 = 50^0$ ( $\angle$ RST = $130^0$ , given)
Thus, $\angle$ QRS = $110^0-50^0 = 60^0$ (From equation (i))

Q4. In Fig. 6.26, if AB $||$ CD, $\angle$ APQ = 50° and $\angle$ PRD = 127°, find x and y .

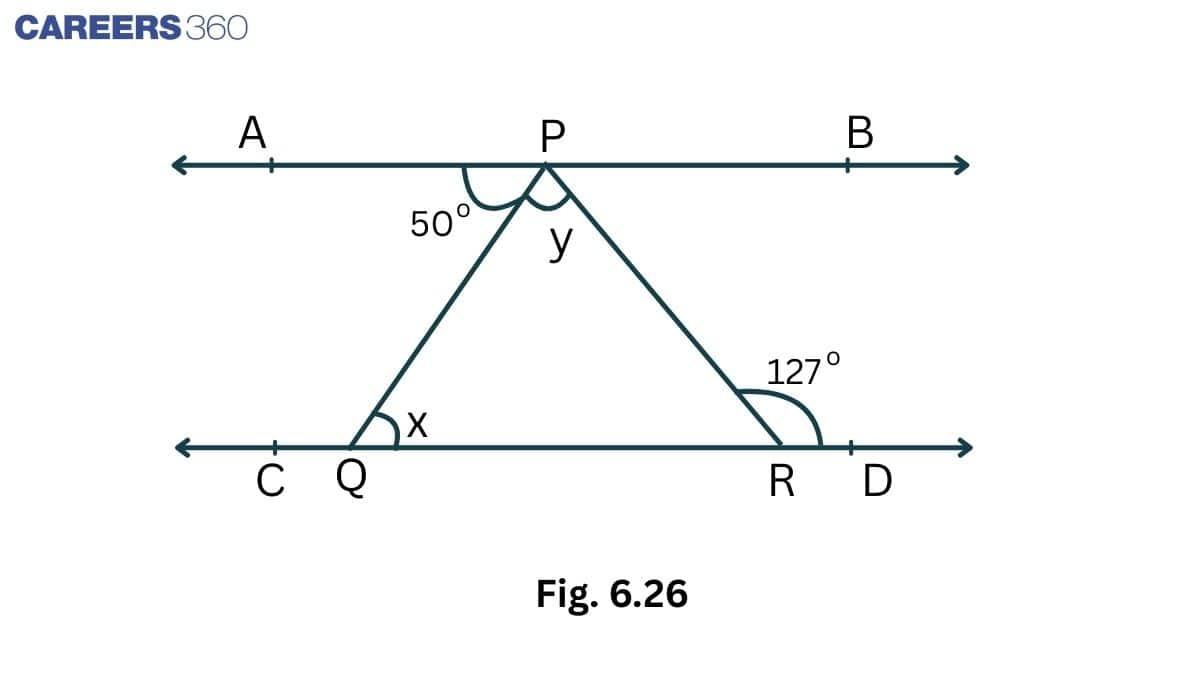
1745305714606

Solution:
Given,
AB || CD, $\angle$ APQ = $50^0$ and $\angle$ PRD = $127^0$
PQ is a transversal. So,
$\angle$ APQ = $\angle$ PQR= $50^0$ (Alternate interior angles)
$\therefore x = 50^0$
Again, PR is a transversal. So,
$\angle$ y + $50^0$ = $127^0$ (Alternate interior angles)
$\Rightarrow y = 77^0$

Q5. In Fig. 6.27, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB $||$ CD.

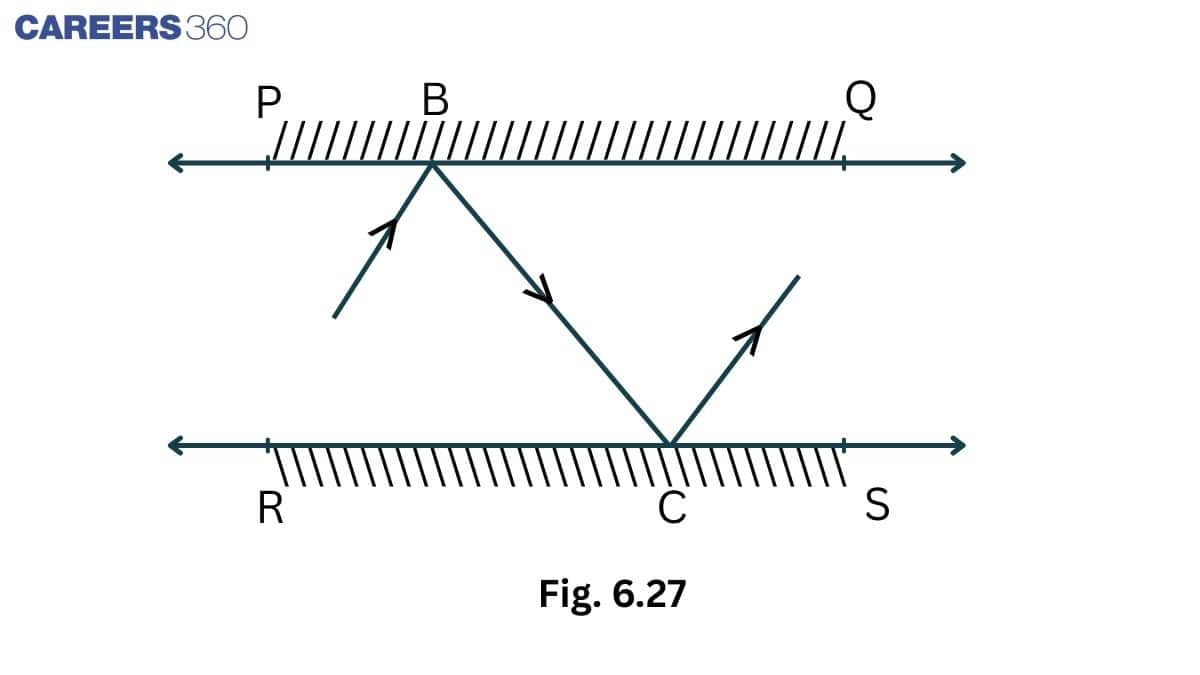
1745305757257

Solution:

Draw a ray BL $\perp$ PQ and CM $\perp$ RSSince PQ || RS (Given)
So, BL || CM and BC is a transversal
$\therefore$ $\angle$ LBC = $\angle$ MCB (Alternate interior angles).............(i)
It is known that, angle of incidence = the angle of reflection
So, $\angle$ ABL = $\angle$ LBC and $\angle$ MCB = $\angle$ MCD
$\Rightarrow \angle ABL =\angle MCD$ ..................(ii)
Adding eq (i) and eq (ii), we get
$\angle$ ABC = $\angle$ DCB
Both the interior angles are equal
Hence AB || CD

Also Read
Lines and Angles Exercise 6.1

Topics covered in Chapter 6, Lines and Angles: Exercise 6.2

The following key concepts are covered in this exercise:
1. Corresponding angles - Angles that are on the same side and corresponding position of the traversal.
2. Alternate interior angles - Angles that are between two parallel lines and on opposite sides of the transversal.
3. Alternate exterior angles - Angles that are on the outside of the two parallel lines and opposite sides of the transversal.
4. Consecutive interior angles - Angles that are on the same side of the transversal and between the two parallel lines.
5. Lines parallel to the same line - If two lines are parallel to the same line, then these two lines are parallel to each other also.

Also See

NCERT Solutions of Class 9 Subject Wise

Students must check the NCERT solutions for Class 9 Maths and Science given below:

Subject-Wise NCERT Exemplar Solutions

Students must check the NCERT exemplar solutions for Class 9 Maths and Science given below:

Frequently Asked Questions (FAQs)

Q: What is the main concept of NCERT solutions for Class 9 Maths exercise 6.2?

This exercise is about Parallel Lines and a Transversal, types of angles like vertically opposite angles and axioms that are formed due to this intersection.

Q: What are parallel lines?

Parallel lines are coplanar straight lines that never intersect with each other at any point.

Q: What do you understand by consecutive interior angle?

Consecutive angles are the angles formed by a transversal that intersects two parallel lines. Each angle forms a pair of consecutive angles which lies on each of the parallel lines on any one side of the transversal which can be either be interior or exterior.

Q: How many angles are formed when a transverse cuts a pair of parallel lines?

Four angles are formed on each of the parallel lines. Thus, making the total sum eight.

Articles

Haryana Open School Admission 2025: Apply Haryana Open Fresh 10th, 12th Online Form

Sep 04, 2025

Gujarat Paramedical Merit List 2025 Revised (Out): Download PDF Rank List

Sep 04, 2025

How to Renew the NSP Scholarship – Step-by-Step Renewal Process & Eligibility

Sep 03, 2025

IOQM Answer Key 2025: Download IOQM Solution PDF for All Sets

Sep 02, 2025

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Read Complete Answer

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Read Complete Answer

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Read Complete Answer

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Read Complete Answer

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is