NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.1 - Lines and Angles

Q1. In Fig. 6.13, lines AB and CD intersect at O. If $\angle$ AOC + $\angle$ BOE = 70° and $\angle$ BOD = 40°, find $\angle$ BOE and reflex $\angle$ COE.

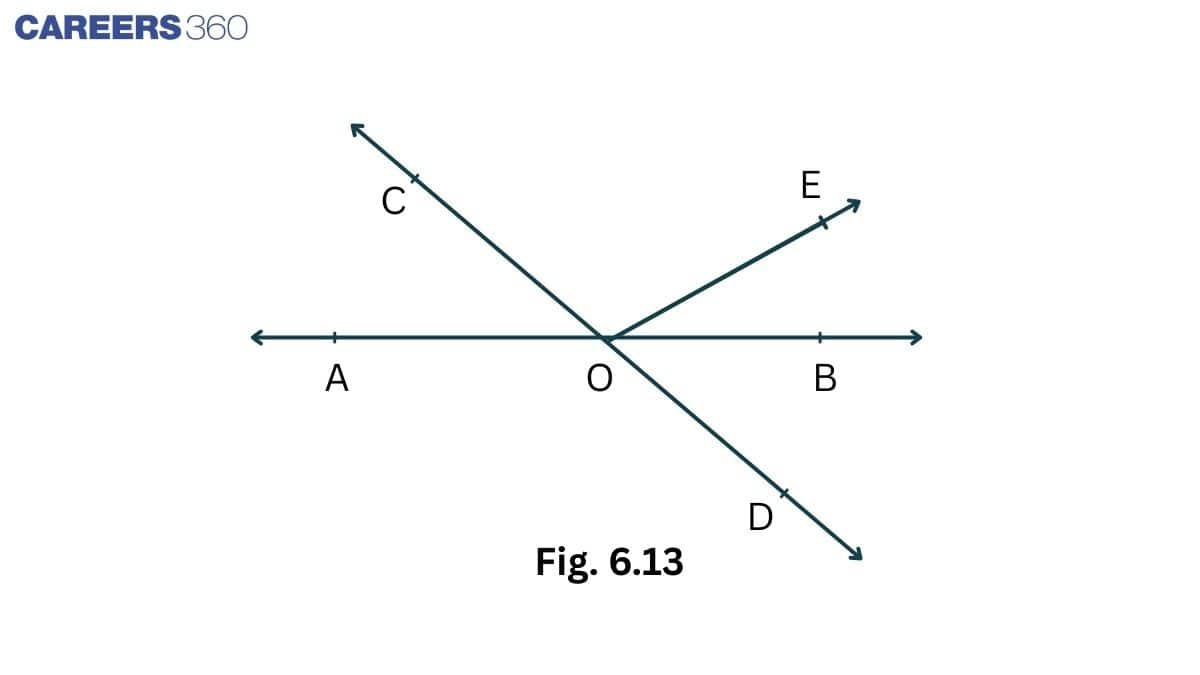
Solution:
Given that,
AB is a straight line. Lines AB and CD intersect at O. $\angle AOC + \angle BOE = 70^0$ and $\angle$ BOD = $40^0$
Since AB is a straight line

$\therefore$ $\angle$ AOC + $\angle$ COE + $\angle$ EOB = $180^0$

$\Rightarrow \angle COE = 180^0-70^0=110^0$ [since $\angle AOC + \angle BOE = 70^0$ ]

So, reflex $\angle$ COE = $360^0-110^0 = 250^0$

It is given that AB and CD intersect at O

Therefore, $\angle$ AOC = $\angle$ BOD [vertically opposite angle]

$\Rightarrow \angle COA = 40^0$ [ GIven $\angle$ BOD = $40^0$ ]

Also, $\angle AOC + \angle BOE = 70^0$

So, $\angle$ BOE = $30^0$

Q2. In Fig. 6.14, lines XY and MN intersect at O. If $\angle POY = 90^o$ and a : b = 2 : 3, find c.

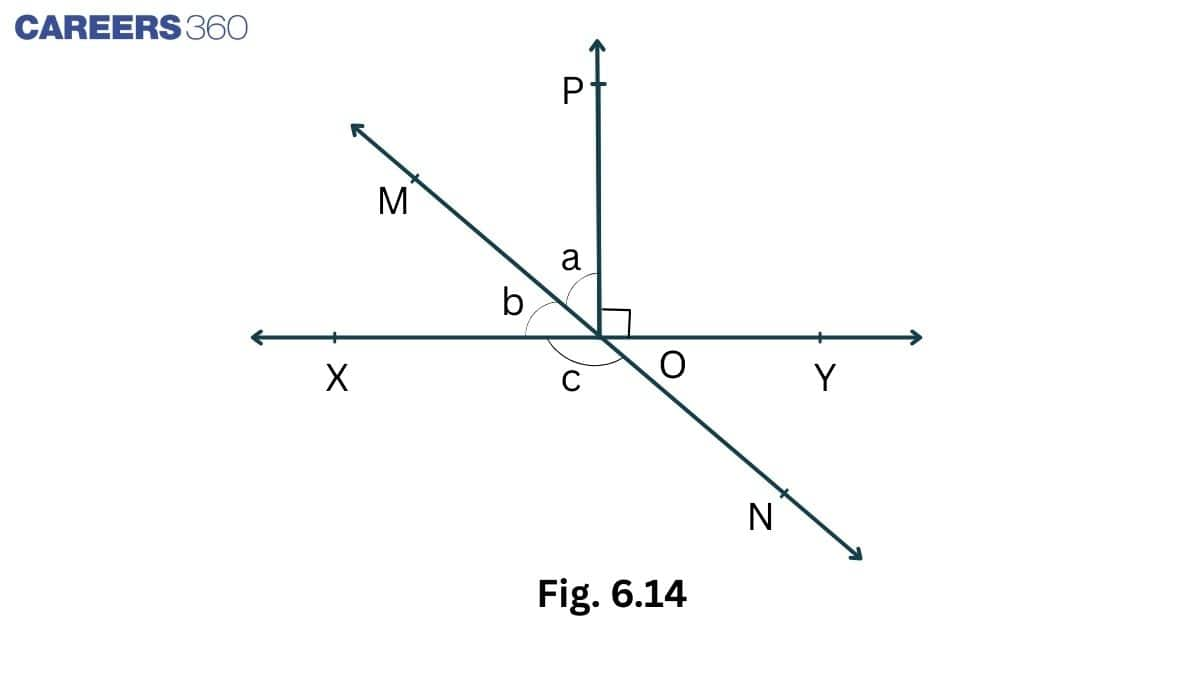
Solution:
Given that,
Line XY and MN intersect at O and $\angle$ POY = $90^0$ also $a:b = 2:3 \Rightarrow b = \frac{3a}{2}$ ..............(i)

Since XY is a straight line

Therefore, $\\a+b+\angle POY = 180^0\\ a+b = 180^0-90^0 = 90^0$ ...........(ii)

Thus, from eq (i) and eq (ii), we get

$\\\Rightarrow \frac{3a}{2}+a = 90^0\\$

$\\\Rightarrow a = 36^0\\$

So, $b = 54^0\\$

Since $\angle$ MOY = $\angle$ c [vertically opposite angles]

$\angle$ a + $\angle$ POY = c

$126^0 =c$

Q3. In Fig. 6.15, $\angle$ PQR = $\angle$ PRQ, then prove that $\angle$ PQS = $\angle$ PRT.

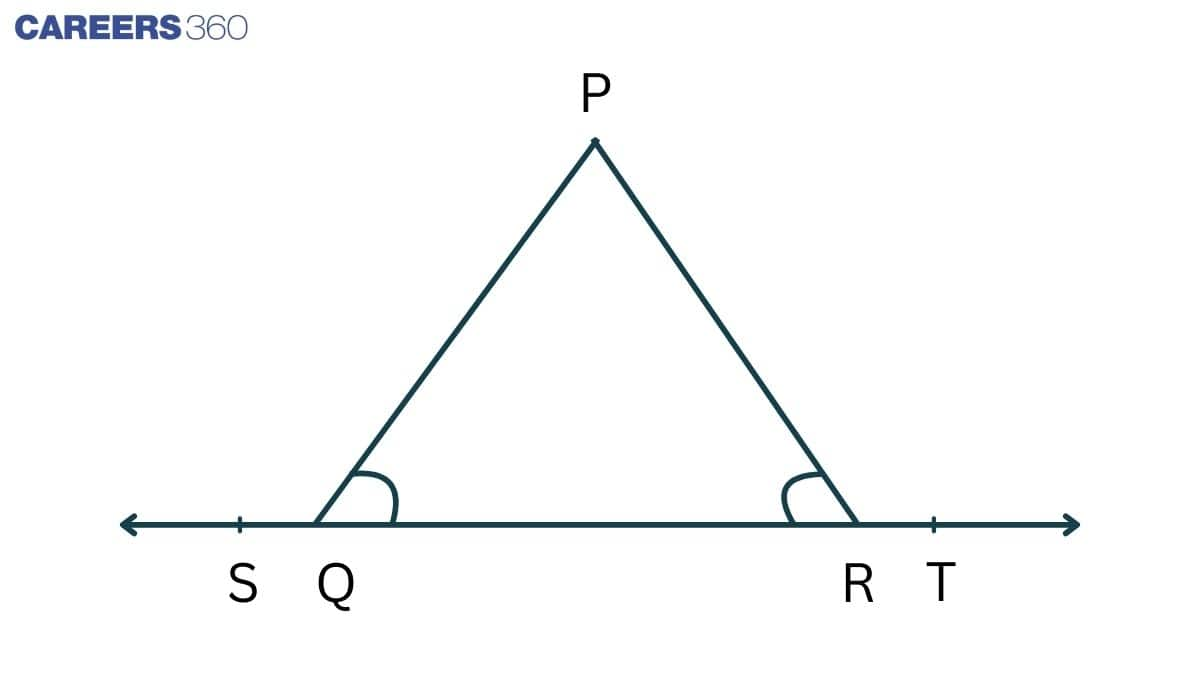
Solution:
Given that,
ABC is a triangle such that $\angle$ PQR = $\angle$ PRQ and ST is a straight line.

Now, $\angle$ PQR + $\angle$ PQS = $180^0$ {Linear pair}............(i)

Similarly, $\angle$ PRQ + $\angle$ PRT = $180^0$ ..................(ii)

equating the eq (i) and eq (ii), we get

$\angle PQR +\angle PQS =\angle PRT + \angle PRQ$ {but $\angle$ PQR = $\angle$ PRQ }

Therefore, $\angle$ PQS = $\angle$ PRT

Hence proved.

Q4 In Fig. 6.16, if x + y = w + z , then prove that AOB is a line.

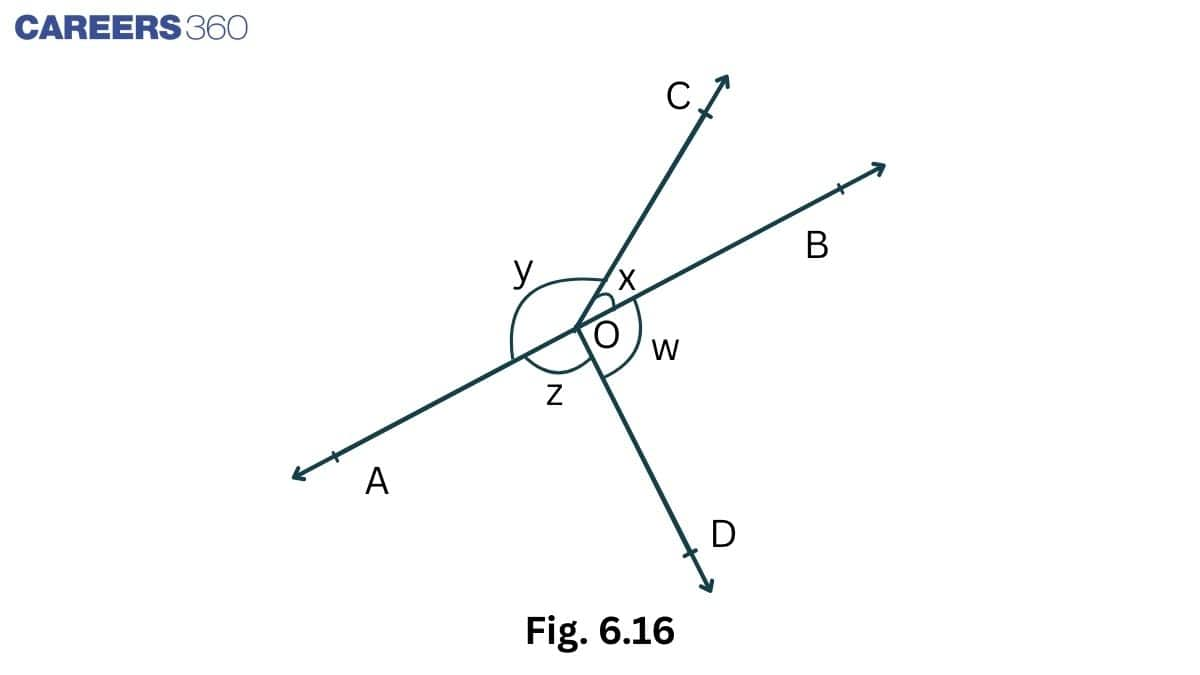
Solution:
Given that,

$x+y = z+w$ ..............(i)

It is known that, the sum of all the angles at a point = $360^0$

$\therefore$ $x+y+z+w=360^0$ ..............(ii)

From eq (i) and eq (ii), we get

$\\2(x+y)=360^0\\ x+y = 180^0$

Hence proved AOB is a line.

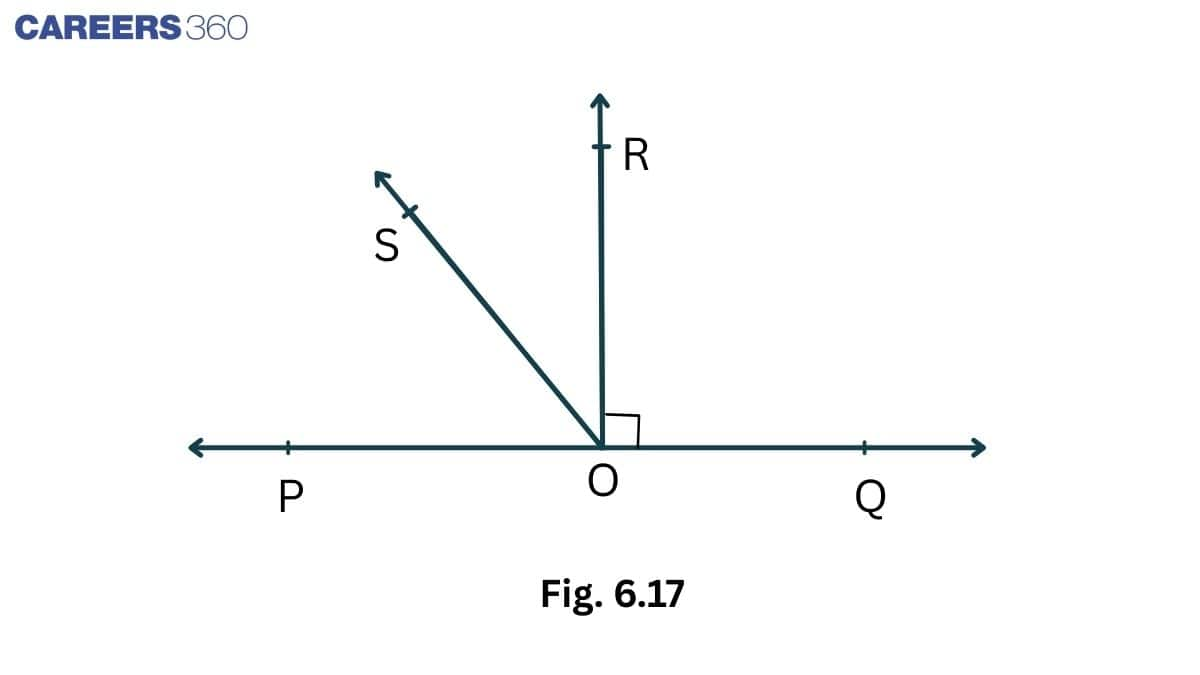
Solution:
Given that,
POQ is a line, OR $\perp$ PQ and $\angle$ ROQ is a right angle.

Now, $\angle$ POS + $\angle$ ROS + $\angle$ ROQ = $180^0$ [since POQ is a straight line]

$\\\Rightarrow \angle POS + \angle ROS = 90^0\\ \Rightarrow \angle ROS = 90^0-\angle POS$ .............(i)

and, $\angle$ ROS + $\angle$ ROQ = $\angle$ QOS

$\angle ROS = \angle QOS -90^0$ ..............(ii)

Add the eq (i ) and eq (ii), we get

$\angle \textup{ROS} = \frac{1}{2}(\angle \textup{QOS} - \angle \textup{POS})$

Hence proved.

Solution:

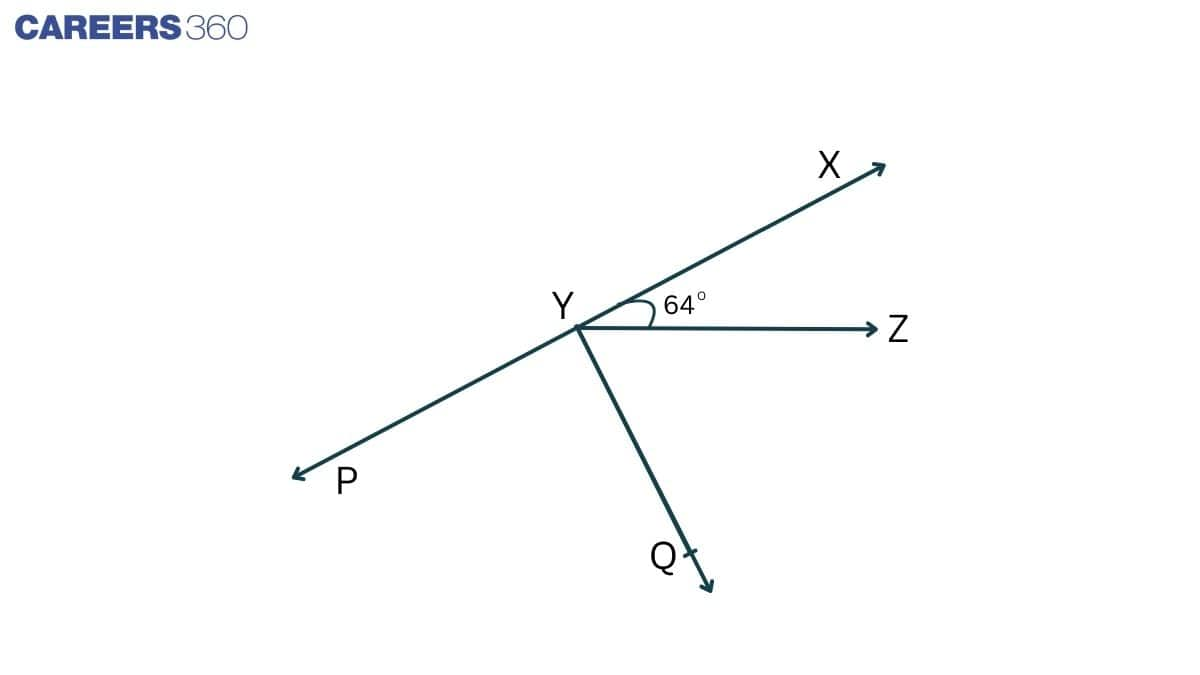
Given that,

$\angle$ XYZ = $64^0$ and XY produced to point P and Ray YQ bisects $\angle$ ZYP $\Rightarrow \angle QYP = \angle ZYQ$
Now, XYP is a straight line

So, $\angle$ XYZ + $\angle$ ZYQ + $\angle$ QYP = $180^0$

$\Rightarrow 2(\angle QYP )=180^0 - 64^0 = 116^0$

$\Rightarrow (\angle QYP )= 58^0$

Thus reflex of $\angle$ QYP = $360^0- 58^0 = 302^0$

Since $\angle$ XYQ = $\angle$ XYZ + $\angle$ ZYQ [ $\because$ $\angle QYP = \angle ZYQ$

$\angle XYQ$ = $64^0+58^0 = 122^0$