NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.2 - Vector Algebra
Exercise 10.2 of Class 12 Maths Chapter 10 helps you understand how to add vectors, find their magnitude, and break them into components, just like combining forces or directions in real life. For example, pilots and sailors use vector addition to navigate through air or water currents. NCERT solution for Class 12 is highly beneficial for Class 12 board exams, along with competitive exams such as JEE Main and others.
Class 12 maths chapter 10 exercise 10.2 solutions is not only beneficial in maths, it has a major contribution to physics also, particularly in topics such as motion, forces and electric field. These NCERT exercise solutions are made by expert faculty with clear, step-by-step methods to make tough problems easier. Practising these builds strong concepts and boosts your confidence for both board exams and competitive exams.
IIT Delhi MTech GATE cut-offs 2026 for the previous year are given below.
IIT Delhi GATE MTech cut-off | ||||
Discipline | GEN | EWS | OBC-NCL | SC/ ST/ PWD |
B.E./B.Tech. (Textile) | ≥ 400 | ≥ 400 | ≥ 360 | ≥ 267 |
B.E./B.Tech.(Non-Textile) /M.Sc. | ≥ 600 | ≥ 600 | ≥ 540 | ≥ 400 |
Degree cut-off | ||||
Percentage Marks | ≥ 60% | ≥ 60% | ≥ 60% | ≥ 55% |
Equivalent CGPA on a 10 point scale | ≥ 6.0 | ≥ 6.0 | ≥ 6.0 | ≥ 5.5 |
This Story also Contains
- Class 12 Maths Chapter 10 Exercise 10.2 Solutions: Download PDF
- NCERT Solutions for Class 12 Maths Chapter 10: Exercise 10.2
- Topics Covered in Maths Chapter 10 Vector Algebra: Exercise 10.2
- NCERT Solutions Subject Wise
- Subject Wise NCERT Exemplar Solutions
Class 12 Maths Chapter 10 Exercise 10.2 Solutions: Download PDF
Access NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.2 to strengthen your understanding of vector operations like addition, scalar multiplication, and components of vectors. These step-by-step NCERT solutions are perfect for the final exam and homework help.
NCERT Solutions for Class 12 Maths Chapter 10: Exercise 10.2
Question 1: Compute the magnitude of the following vectors:
(1) $\vec a = \hat i + \hat j + \hat k$
Answer:
Here
$\vec a = \hat i + \hat j + \hat k$
Magnitude of $\vec a$
$\vec a=\sqrt{1^2+1^2+1^2}=\sqrt{3}$
Question 1: Compute the magnitude of the following vectors:
(2) $\vec b = 2 \hat i - 7 \hat j - 3 \hat k$
Answer:
Here,
$\vec b = 2 \hat i - 7 \hat j - 3 \hat k$
Magnitude of $\vec b$
$\left | \vec b \right |=\sqrt{2^2+(-7)^2+(-3)^2}=\sqrt{62}$
Question 1: Compute the magnitude of the following vectors:
(3) $\vec c = \frac{1}{\sqrt 3 }\hat i + \frac{1}{\sqrt 3 }\hat j -\frac{1}{\sqrt 3 }\hat k$
Answer:
Here,
$\vec c = \frac{1}{\sqrt 3 }\hat i + \frac{1}{\sqrt 3 }\hat j -\frac{1}{\sqrt 3 }\hat k$
Magnitude of $\vec c$
$\left |\vec c \right |=\sqrt{\left ( \frac{1}{\sqrt{3}} \right )^2+\left ( \frac{1}{\sqrt{3}} \right )^2+\left ( \frac{1}{\sqrt{3}} \right )^2}=1$
Question 2: Write two different vectors having same magnitude
Answer:
Two different Vectors having the same magnitude are
$\vec a= 3\hat i+6\hat j+9\hat k$
$\vec b= 9\hat i+6\hat j+3\hat k$
The magnitude of both vector
$\left | \vec a \right |=\left | \vec b \right | = \sqrt{9^2+6^2+3^2}=\sqrt{126}$
Question 3: Write two different vectors having same direction.
Answer:
Two different vectors having the same direction are:
$\vec a=\hat i+2\hat j+3\hat k$
$\vec b=2\hat i+4\hat j+6\hat k$
Question 4: Find the values of x and y so that the vectors $2 \hat i + 3 \hat j$ and $x \hat i + y \hat j$ are equal.
Answer:
$2 \hat i + 3 \hat j$ will be equal to $x \hat i + y \hat j$ when their corresponding components are equal.
Hence when,
$x=2$ and
$y=3$
Question 5: Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).
Answer:
Let point P = (2, 1) and Q = (– 5, 7).
Now,
$\vec {PQ}=(-5-2)\hat i+(7-1)\hat j=-7\hat i +6\hat j$
Hence scalar components are (-7,6) and the vector is $-7\hat i +6\hat j$
Answer:
Given,
$\\ \vec a = \hat i - 2 \hat j + \hat k ,\\ \vec b = -2 \hat i + 4 \hat j + 5 \hat k \: \: and\: \: \: \\\vec c = \hat i - 6 \hat j - 7 \hat k$
Now, The sum of the vectors:
$\vec a +\vec b+\vec c = \hat i - 2 \hat j + \hat k + -2 \hat i + 4 \hat j + 5 \hat k + \hat i - 6 \hat j - 7 \hat k$
$\vec a +\vec b+\vec c = (1-2+1)\hat i +(-2+4-6) \hat j + (1+5-7)\hat k$
$\vec a +\vec b+\vec c =-4\hat j-\hat k$
Question 7: Find the unit vector in the direction of the vector $\vec a = \hat i + \hat j + 2 \hat k$
Answer:
Given
$\vec a = \hat i + \hat j + 2 \hat k$
Magnitude of $\vec a$
$\left |\vec a \right |=\sqrt{1^2+1^2+2^2}=\sqrt{6}$
A unit vector in the direction of $\vec a$
$\vec u = \frac{\hat i}{\left | a \right |} + \frac{\hat j}{\left | a \right |} +\frac{2\hat k}{\left | a \right |} =\frac{\hat i}{\sqrt{6}}+\frac{\hat j}{\sqrt{6}}+\frac{2\hat k}{\sqrt{6}}$
Answer:
Given P = (1, 2, 3) and Q = (4, 5, 6)
A vector in direction of PQ
$\vec {PQ}=(4-1)\hat i+(5-2)\hat j +(6-3)\hat k$
$\vec {PQ}=3\hat i+3\hat j +3\hat k$
Magnitude of PQ
$\left | \vec {PQ} \right |=\sqrt{3^2+3^2+3^2}=3\sqrt{3}$
Now, unit vector in direction of PQ
$\hat u=\frac{\vec {PQ}}{\left | \vec {PQ} \right |}=\frac{3\hat i+3\hat j+3\hat k}{3\sqrt{3}}$
$\hat u=\frac{\hat i}{\sqrt{3}}+\frac{\hat j}{\sqrt{3}}+\frac{\hat k}{\sqrt{3}}$
Answer:
Given
$\vec a = 2 \hat i - \hat j + 2 \hat k$
$\vec b = - \hat i + \hat j - \hat k$
Now,
$\vec a + \vec b=(2-1)\hat i+(-1+1)\hat j+ (2-1)\hat k$
$\vec a + \vec b=\hat i+\hat k$
Now a unit vector in the direction of $\vec a + \vec b$
$\vec u= \frac{\vec a + \vec b}{\left |\vec a + \vec b \right |}=\frac{\hat i+\hat j}{\sqrt{1^2+1^2}}$
$\vec u= \frac{\hat i}{\sqrt{2}}+\frac{\hat j}{\sqrt{2}}$
Question 10: Find a vector in the direction of vector $5 \hat i - \hat j + 2 \hat k$ which has magnitude 8 units.
Answer:
Given a vector
$\vec a=5 \hat i - \hat j + 2 \hat k$
the unit vector in the direction of $5 \hat i - \hat j + 2 \hat k$
$\vec u=\frac{5\hat i - \hat j + 2 \hat k}{\sqrt{5^2+(-1)^2+2^2}}=\frac{5\hat i}{\sqrt{30}}-\frac{\hat j}{\sqrt{30}}+\frac{2\hat k}{\sqrt{30}}$
A vector in direction of $5 \hat i - \hat j + 2 \hat k$ and whose magnitude is 8 =
$8\vec u=\frac{40\hat i}{\sqrt{30}}-\frac{8\hat j}{\sqrt{30}}+\frac{16\hat k}{\sqrt{30}}$
Question 11: Show that the vectors $2 \hat i -3 \hat j + 4 \hat k$ and $- 4 \hat i + 6 \hat j - 8 \hat k$ are collinear.
Answer:
Let
$\vec a =2 \hat i -3 \hat j + 4 \hat k$
$\vec b=- 4 \hat i + 6 \hat j - 8 \hat k$
It can be seen that
$\vec b=- 4 \hat i + 6 \hat j - 8 \hat k=-2(2 \hat i -3 \hat j + 4 \hat k)=-2\vec a$
Hence here $\vec b=-2\vec a$
As we know
Whenever we have $\vec b=\lambda \vec a$ , the vector $\vec a$ and $\vec b$ will be colinear.
Here $\lambda =-2$
Hence vectors $2 \hat i -3 \hat j + 4 \hat k$ and $- 4 \hat i + 6 \hat j - 8 \hat k$ are collinear.
Question 12: Find the direction cosines of the vector $\hat i + 2 \hat j + 3 \hat k$
Answer:
Let
$\vec a=\hat i + 2 \hat j + 3 \hat k$
$\left |\vec a \right |=\sqrt{1^2+2^2+3^2}=\sqrt{14}$
Hence direction cosine of $\vec a$ are
$\left ( \frac{1}{\sqrt{14}},\frac{2}{\sqrt{14}} ,\frac{3}{\sqrt{14}}\right )$
Question 13: Find the direction cosines of the vector joining the points A(1, 2, –3) and B(–1, –2, 1), directed from A to B.
Answer:
Given
point A=(1, 2, –3)
point B=(–1, –2, 1)
Vector joining A and B Directed from A to B
$\vec {AB}=(-1-1)\hat i +(-2-2)\hat j+(1-(-3))\hat k$
$\vec {AB}=-2\hat i +-4\hat j+4\hat k$
$\left | \vec {AB} \right |=\sqrt{(-2)^2+(-4)^2+4^2}=\sqrt{36}=6$
Hence Direction cosines of vector AB are
$\left ( \frac{-2}{6},\frac{-4}{6},\frac{4}{6} \right )=\left ( \frac{-1}{3},\frac{-2}{3},\frac{2}{3} \right )$
Question 14: Show that the vector $\hat i + \hat j + \hat k$ is equally inclined to the axes OX, OY and OZ.
Answer:
Let
$\vec a=\hat i + \hat j + \hat k$
$\left | \vec a \right |=\sqrt{1^2+1^2+1^2}=\sqrt{3}$
Hence direction cosines of this vectors is
$\left ( \frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right )$
Let $\alpha$ , $\beta$ and $\gamma$ be the angle made by x-axis, y-axis and z- axis respectively
Now as we know,
$cos\alpha=\frac{1}{\sqrt{3}}$ , $cos\beta=\frac{1}{\sqrt{3}}$ $and\:cos\gamma=\frac{1}{\sqrt{3}}$
Hence Given vector is equally inclined to axis OX,OY and OZ.
Answer:
As we know
The position vector of the point R which divides the line segment PQ in ratio m:n internally:
$\vec r=\frac{m\vec b+n\vec a}{m+n}$
Here
position vector os P = $\vec a$ = $i + 2 j - k$
the position vector of Q = $\vec b=- i + j + k$
m:n = 2:1
And Hence
$\vec r = \frac{2(-\hat i+\hat j +\hat k)+1(\hat i+2\hat j-\hat k)}{2+1}=\frac{-2\hat i+2\hat j +2\hat k+\hat i+2\hat j-\hat k}{3}$
$\vec r = \frac{-2\hat i+2\hat j +2\hat k+\hat i+2\hat j-\hat k}{3}=\frac{-\hat i+4\hat j+\hat k}{3}$
$\vec r = \frac{-\hat i}{3}+\frac{4\hat j}{3}+\frac{\hat k}{3}$
Answer:
As we know
The position vector of the point R which divides the line segment PQ in ratio m:n externally:
$\vec r=\frac{m\vec b-n\vec a}{m-n}$
Here
position vector os P = $\vec a$ = $i + 2 j - k$
the position vector of Q = $\vec b=- i + j + k$
m:n = 2:1
And Hence
$\vec r = \frac{2(-\hat i+\hat j +\hat k)-1(\hat i+2\hat j-\hat k)}{2-1}=\frac{-2\hat i+2\hat j +2\hat k-\hat i-2\hat j+\hat k}{1}$
$\vec r = -3\hat i +3\hat k$
Question 16: Find the position vector of the mid point of the vector joining the points P(2, 3, 4) and Q(4, 1, –2).
Answer:
Given
The position vector of point P = $2\hat i+3\hat j +4\hat k$
Position Vector of point Q = $4\hat i+\hat j -2\hat k$
The position vector of R which divides PQ in half is given by:
$\vec r =\frac{2\hat i+3\hat j +4\hat k+4\hat i+\hat j -2\hat k}{2}$
$\vec r =\frac{6\hat i+4\hat j +2\hat k}{2}=3\hat i+2\hat j +\hat k$
Answer:
Given
the position vector of A, B, and C are
$\\\vec a = 3 \hat i - 4 \hat j - 4 \hat k ,\\\vec b = 2 \hat i - \hat j + \hat k \: \: and \\\vec c = \hat i - 3 \hat j - 5 \hat k$
Now,
$\vec {AB}=\vec b-\vec a=-\hat i+3\hat j+5\hat k$
$\vec {BC}=\vec c-\vec b=-\hat i-2\hat j-6\hat k$
$\vec {CA}=\vec a-\vec c=2\hat i-\hat j+\hat k$
$\left | \vec {AB} \right |=\sqrt{(-1)^2+3^2+5^2}=\sqrt{35}$
$\left | \vec {BC} \right |=\sqrt{(-1)^2+(-2)^2+(-6)^2}=\sqrt{41}$
$\left | \vec {CA} \right |=\sqrt{(2)^2+(-1)^2+(1)^2}=\sqrt{6}$
As we can see
$\left | \vec {BC} \right |^2=\left | \vec {CA} \right |^2+\left | \vec {AB} \right |^2$
Hence, ABC is a right angle triangle.
Question 18: In triangle ABC (Fig 10.18), which of the following is not true:
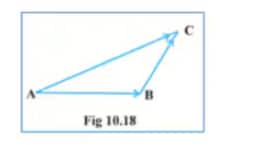
Answer:
From triangles law of addition we have,
$\vec {AB}+\vec {BC}=\vec {AC}$
From here
$\vec {AB}+\vec {BC}-\vec {AC}=0$
also
$\vec {AB}+\vec {BC}+\vec {CA}=0$
Also
$\vec {AB}-\vec {CB}+\vec {CA}=0$
Hence options A,B and D are true SO,
Option C is False.
Answer:
(A) If two vectors are collinear then, they have the same direction or are parallel or antiparallel.Therefore, They can be expressed in the form $\vec{b}=\lambda \vec{a}$ where a and b are vectors and $\lambda$ is some scalar quantity. Therefore, (A) is true.
(B) $\lambda$ is a scalar quantity so its value may be equal to $\pm 1$ is the obvious result. Therefore, ( B ) is also true.
(C) The vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$ are proportional, Therefore, (C) is not true.
(D) The vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$ can have different magnitudes as well as different directions. Therefore, (D) is not true. Therefore, the incorrect options are (C) and (D).
Topics Covered in Maths Chapter 10 Vector Algebra: Exercise 10.2
Addition of Vectors:
A vector $\overrightarrow{\mathrm{AB}}$ simply means the displacement from a point A to the point B. Now consider a situation that a girl moves from $A$ to $B$ and then from $B$ to $C$ (Fig 10.7). The net displacement made by the girl from point $A$ to the point $C$, is given by the vector $\overrightarrow{A C}$ and expressed as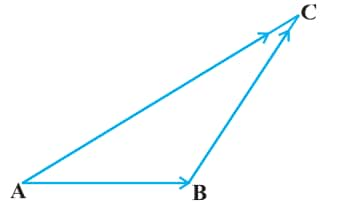
$
\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}
$
This is known as the triangle law of vector addition.
Multiplication of a Vector by a Scalar:
Let $\vec{a}$ be a given vector and $\lambda$ a scalar. Then the product of the vector $\vec{a}$ by the scalar $\lambda$, denoted as $\lambda \vec{a}$, is called the multiplication of vector $\vec{a}$ by the scalar $\lambda$. Note that, $\lambda \vec{a}$ is also a vector, collinear to the vector $\vec{a}$. The vector $\lambda \vec{a}$ has the direction same (or opposite) to that of vector $\vec{a}$ according as the value of $\lambda$ is positive (or negative). Also, the magnitude of vector $\lambda \vec{a}$ is $|\lambda|$ times the magnitude of the vector $\vec{a}$, i.e.,
$
|\lambda \vec{a}|=|\lambda||\vec{a}|
$
Also Read
- Vector Algebra Exercise 10.1
- Vector Algebra Exercise 10.3
- Vector Algebra Exercise 10.4
- Vector Algebra Miscellaneous Exercise
Also see-
NCERT Solutions Subject Wise
- NCERT Solutions Class 12 Chemistry
- NCERT Solutions for Class 12 Physics
- NCERT Solutions for Class 12 Biology
- NCERT Solutions for Class 12 Mathematics
Subject Wise NCERT Exemplar Solutions
Frequently Asked Questions (FAQs)
Yes, two different vectors can have the same direction. It can be vectors with different magnitudes. The third question of exercise 10.2 Class 12 Maths gives an example of this.
The question may be to find a unit vector in the direction of a given vector, or it may be related to collinear vectors etc.
There are a total of 19 questions. Practising these may help in the CBSE Class 12 Maths Paper
The concepts in Vector Algebra help to solve NEET physics problems. A good part of Class 11 and Class 12 NCERT Physics Syllabus uses the concepts of vectors. So vectors will be useful for the NEET exam as well as for engineering entrance exams like JEE Main.
The given vectors are equal. Which implies that 2x=7. Therefore x=3.5. And 3y=6, therefore y=2
One method to solve such kinds of problems is to find the magnitudes of given vectors and verify Pythagoras Theorem.
Yes, two different vectors can have the same magnitude. These vectors may be pointing in a different direction. An example is shown in question number 2 of NCERT solutions for Class 12 Maths chapter 10 exercise 10.2.
Questions related to CBSE Class 12th
On Question asked by student community
Hello,
Yes, it's completely fine to skip this year's 12th board exams and give them next year as a reporter or private candidate, allowing you to prepare better; the process involves contacting your current school or board to register as a private candidate or for improvement exams during the specified
HELLO,
Yes i am giving you the link below through which you will be able to download the Class 12th Maths Book PDF
Here is the link :- https://school.careers360.com/ncert/ncert-book-for-class-12-maths
Hope this will help you!
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your
The CBSE Sahodaya Class 12 Pre-Board Chemistry Question Paper for the 2025-2026 session is available for download on the provided page, along with its corresponding answer key.
The Sahodaya Pre-Board exams, conducted in two rounds (Round 1 typically in December 2025 and Round 2 in January 2026), are modeled precisely
Hello,
You can get the Class 11 English Syllabus 2025-26 from the Careers360 website. This resource also provides details about exam dates, previous year papers, exam paper analysis, exam patterns, preparation tips and many more. you search in this site or you can ask question we will provide you the
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
