• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT solutions for class 12 chemistry chapter 4 Chemical Kinetics

NCERT solutions for class 12 chemistry chapter 4 Chemical Kinetics

Edited By Vishal kumar | Updated on Mar 06, 2023 12:05 PM IST | #CBSE Class 12th
Upcoming Event
CBSE Class 12th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics- Students appearing in the Class 12 board exam must check these NCERT Class 12 Chemistry Chapter 4 solutions. NCERT solutions for Class 12 Chemistry chapter 4 Chemical Kinetics covers all the questions from NCERT books for Class 12 Chemistry.

In NCERT Class 12 Chemistry solutions chapter 4, there are questions and solutions of some important topics like average and instantaneous rate of a reaction, factors affecting the rate of reaction, integrated rate equations for zero and first-order reactions, etc. Read further to know all the Chemical Kinetics Class 12 exercise solutions.

Also Read,

Check NCERT Class 12 solutions for other subjects.

Rate of reaction- It is defined as the rate of change in concentration of reactant or product. Unit of rate is mole\:L^{-1}S^{-1} .

Reactants, R \rightarrow Products, P

nA+mB \rightarrow pC+qD

Rate=-\frac{1}{n}\frac{\Delta \left [ A \right ]}{\Delta t}=-\frac{1}{m}\frac{\Delta \left [ B \right ]}{\Delta t}=+\frac{1}{p}\frac{\Delta \left [ C \right ]}{\Delta t}=+\frac{1}{n}\frac{\Delta \left [ D \right ]}{\Delta t}

NCERT solutions for class 12 chemistry chapter 4 Chemical Kinetics -

Question 4.1 For the reaction R\rightarrow P , the concentration of a reactant change from 0.03M to 0.02M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.

Answer :

We know that,

The average rate of reaction = \frac{-\Delta [R]}{\Delta t}

= -\frac{ [R]_{2}-[R]_{1}}{t_{2}-t_{1}}

= \frac{0.03-0.02}{25}Mmin^{-1}

= 4\times 10^{-4}Mmin^{-1}

In seconds we need to divide it by 60. So,

= \frac{4\times 10^{-4}}{60}Msec^{-1}

= 6.67 \times 10^{-6}Msec^{-1}


Question 4.2 In a reaction, 2A\rightarrow Products P, the concentration of A decreases from 0.5 mol L^{-1} to 0.4 mol L^{-1} in 10 minutes. Calculate the rate during this interval?

Answer :

According to the formula of an average rate

= -\frac{1}{2}\frac{\Delta[ A]}{\Delta t} (final concentration - initial conc.)/time interval

= -\frac{1}{2}\frac{[ A]_{2}-[A]_{1}}{t_{2}-t_{1}}

= -\frac{1}{2}\frac{[ 0.4]-[0.5]}{10}

= \frac{0.1}{20}Mmin^{-1}

= 5\times 10^{-3}Mmin^{-1}

Question 4.3 For a reaction, A+B\rightarrow product ; the rate law is given by, r=k\left [ A \right ]^{1/2}\left [ B \right ]^{2} . What is the order of the reaction?

Answer :

Order of reaction = Sum of power of concentration of the reactant in the rate law expressions

So, here the power of A = 0.5

and power of B = 2

order of reaction = 2+0.5 =2.5

Question 4.4 The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y ?

Answer :

The order of a reaction means the sum of the power of concentration of the reactant in rate law expression.

So rate law expression for the second-order reaction is R=k[x]^{2} here R = rate

if the concentration is increased to 3 times means x^{'}_{new}=3x

new rate law expression = R^{'}=k[3x]^{2} = 9k[x]^{2} = 9R

the rate of formation of Y becomes 9 times faster than before

Question 4.5 A first order reaction has a rate constant 1.15\times 10^{-3}s^{-1} . How long will 5g of his reactant take to reduce to 3g ?

Answer :

Given data,

initial conc. = 5g

final conc. = 3g

rate const. for first-order = 1.15\times 10^{-3}s^{-1}

We know that for the first-order reaction,

t=\frac{2.308}{k}\log\frac{[R]_{0}}{[R]}

=\frac{2.308}{1.15\times 10^{-3}}\log\frac{5}{3} [log(5/3)= 0.2219]

= 444.38 sec (approx)

Question 4.6 Time required to decompose SO_{2}Cl_{2} to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.

Answer :

We know that t(half ) for the first-order reaction is \frac{0.693}{k} = t_{1/2}

and we have given the value of half time t_{1/2} = 60 min

thus, k = \frac{0.693}{60}min^{-1}

= 0.01155 /min

OR = 1.1925 \times 10^{-4}sec

Alternative method

we can also solve this problem by using the first-order reaction equation.

k = \frac{2.303}{t}\log\frac{[R]_{0}}{[R]}

put [R]=[R_{0}]/2

Question 4.7 What will be the effect of temperature on rate constant ?

Answer :

The rate constant of the reaction is nearly doubled on rising in 10-degree temperature.

Arrhenius equation depicts the relation between temperature and rates constant.

k = Ae^{-\frac{E_{a}}{RT}}

A= Arrhenius factor

Ea = Activation energy

R = gas constant

T = temperature

Question 4.8 The rate of the chemical reaction doubles for an increase of 10K in absolute temperature from 298K Calculate E_{a} .

Answer :

Given data

T_{1} (initial temperature) = 298K and T_{2} (final temperature)= 308K

And we know that rate of reaction is nearly doubled when temperature rise 10-degree

So, \frac{k_{2}}{k_{1}}=2 and R = 8.314 J/mol/K

now, \log\frac{k_{2}}{k_{1}}=\frac{ E_{a}}{2.303}[\frac{T_{2}-T_{1}}{T_{1}T_{2}}]

On putting the value of given data we get,

\log2=\frac{ E_{a}}{2.303}[\frac{10}{298\times 308}]

Activation energy ( E_{a} ) = \frac{2.303\times 8.314\times 298\times 308\times \log2}{10}Jmol^{-1}

=52.9 KJ/mol(approx)

Question 4.9 The activation energy for the reaction 2HI(g)\rightarrow H_{2}+I_{2}(g) is 209.5 KJ mol^{-1} at 518 K . Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?

Answer :

We have

Activation energy = 209.5KJ/mol

temperature= 581K

R = 8.314J/mol/K

Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as

x= e^{-E_{a}/RT}

taking log both sides we get

\log x = -\frac{E_{a}}{RT}

=\frac{209500Jmol^{-1}}{2.303\times 8.314Jmol^{-1}K^{-1}\times 581}

= 18.832

x = antilog(18.832)

= 1.471 \times 10^{-19}

NCERT Solutions for class 12 chemistry chapter 4

Question 4.1(i) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

3NO(g)\rightarrow N_{2}O\: \: Rate= k\left [ NO \right ]^{2}

Answer :

Given pieces of information

Rate = k[NO]^{2}

so the order of the reaction is 2

The dimension of k = Rate/[NO]^{2}

\\=molL^{-1}s^{-1}/mol^{2}L^{-2}\\ =L\ mol^{-1}\ s ^{-1}


Question 4.1(ii) From the rate expression for the following reactions determine their order of reaction and the dimensions of the rate constants.

(ii) H_{2}O_{2}(aq)+3I^{-}(aq)+2H^{+}\rightarrow 2H_{2}O(I)+I_{3}^{-} Rate=k\left [ H_{2}O_{2}\right ]\left [ I^{-} \right ]

Answer :

Given rate = k[H_{2}O_{2}][I^{-}]

therefore the order of the reaction is 2

Dimension of k = rate/[H_{2}O_{2}][I^{-}]

\\=mol\ L^{-1}\ s^{-1}/(mol\ L^{-1})(mol\ L^{-1})\\ =L\ mol^{-1}\ s^{-1}

Question 4.1(iii) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

CH_{3}CHO(g)\rightarrow CH_{4}(g)+CO(g)\: \: Rate=k\left [ CH_{3} CHO\right ]^{3/2}

Answer :

Given Rate = k[CH_{3}CHO]^{3/2}

therefore the order of the reaction is 3/2

and the dimension of k =Rate/[CH_{3}CHO]^{3/2}

\\=molL^{-1}s^{-1}/(molL^{-1})^{3/2}\\ =molL^{-1}s^{-1}/mol^{3/2}L^{-3/2}\\ =L^{1/2}\ mol^{-1/2}\ s^{-1}

Question 4.1(iv) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

C_{2}H_{5}Cl(g\rightarrow )C_{2}H_{4}(g)+HCL(g) \: Rate=k\left [ C_{2}H_{5}Cl \right ]

Answer :

rate = k[C_{2}H_{5}Cl]

so the order of the reaction is 1

and the dimension of k = rate/[C_{2}H_{5}Cl]

\\=molL^{-1}s^{-1}/mol L^{-1}\\ =s^{-1}

Question 4.2 For the reaction:
2A+B\rightarrow A_{2}B
the rate = k\left [ A \right ]\left [ B \right ]^{2} with k=2.0\times 10^{-6}mol^{-2}L^{2}s^{-1} . Calculate the initial rate of the reaction when \left [ A \right ]=0.1 mol L^{-1}\: \: ,\left [ B \right ]=0.2 mol L^{-1} . Calculate the rate of reaction after \left [ A \right ] is reduced to 0.06molL ^{-1} .

Answer :

The initial rate of reaction =

rate = k[A][B]^{2}

substitute the given values of [A], [B] and k,

rate = 2\times 10^{-6}\times 0.1\times (0.2)^{2}

=8 \times 10^{-9}mol^{-2}\ L^{2}\ s^{-1}

When [A] is reduced from 0.1 mol/L to 0.06 mol/L [A^{'}=0.06]

So, conc. of A reacted = 0.1-0.06 = 0.04 mol/L

and conc. of B reacted = 1/2(0.04) = 0.02mol/L

conc. of B left = (0.2-0.02) = 0.18 mol/L [B^{'}=0.18]

Now, the rate of the reaction is (R) = k[A^{'}][B^{'}]

=2\times 10^{-6}\times 0.06\times (0.18)^{2}

= 3.89\times 10^{-6} mol L^{-1}s^{-1}

Question 4.3 The decomposition of NH_{3} on platinum surface is zero order reaction. What are the rates of production of N_{2} and H_{2} if k=2.5\times 10^{-4}mol^{-1}L s^{-1} ?

Answer :

The decomposition of NH_{3} on the platinum surface reaction

2NH_{3}(s)\overset{Pt}{\rightarrow}N_{2}(g)+3H_{2}(g)

therefore,

Rate = -\frac{1}{2}\frac{d[NH_{3}]}{dt}=\frac{d[N_{2}]}{dt}=\frac{1}{3}\frac{d[H_{2}]}{dt}

For zero order reaction rate = k

therefore, -\frac{1}{2}\frac{d[NH_{3}]}{dt}=\frac{d[N_{2}]}{dt}=\frac{1}{3}\frac{d[H_{2}]}{dt}=k

So \frac{d[N_{2}]}{dt}= 2.5\times 10^{-4}mol\ L^{-1}\ s^{-1}

and the rate of production of dihydrogen (H_{2}) = 3 \times (2.5 \times 10^{-4} ) mol\ L^{-1}\ s^{-1}

= 7.5 \times 10^{-4} mol\ L^{-1}\ s^{-1}

Question 4.4 The decomposition of dimethyl ether leads to the formation of CH_{4}, H_{2} and CO and the reaction rate is given by Rate=k\left [ CH_{3}OCH_{3} \right ]^{3/2}The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,Rate=k\left [ P_{CH_{3}OCH_{3} \right ]^{3/2} If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?

Answer :

Given that

rate = k(P_{CH_{3}OCH_{3}})^{3/2}

So, the unit of rate is bar/min .( bar\ min^{-1} )

And thus the unit of k = unit of rate /(bar)^{3/2}

\\=bar\ min^{-1}/(bar)^{3/2}\\ =bar^{-1/2}min^{-1}

Question 4.5 Mention the factors that affect the rate of a chemical reaction.

Answer :

The following factors that affect the rate of reaction-

  • the concentration of reactants
  • temperature, and
  • presence of catalyst

Question 4.6(i) A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is doubled

Answer :

Let assume the concentration of reactant be x

So, rate of reaction, R =k[x]^{2}

Now, if the concentration of reactant is doubled then x\rightarrow 2x . So the rate of reaction would be R = k[2x]^{2} = 4kx^{2}=4R

Hence we can say that the rate of reaction increased by 4 times.

Question 4.6(ii) A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is reduced to half ?

Answer :

Let assume the concentration of reactant be x

So, rate of reaction, R = k[x]^{2}

Now, if the concentration of reactant is doubled then x\rightarrow \frac{x}{2} . So the rate of reaction would be R = k[\frac{x}{2}]^{2} = \frac{kx^{2}}{4}=\frac{R}{4}

Hence we can say that the rate of reaction reduced to 1/4 times.

Question 4.7 What is the effect of temperature on the rate constant of a reaction? How can this effect of temperature on rate constant be represented quantitatively?

Answer :

The rate constant is nearly double when there is a 10-degree rise in temperature in a chemical reaction.

effect of temperature on rate constant be represented quantitatively by Arrhenius equation,

K =Ae^{-E_{a}/RT} where k is rate constant

A is Arrhenius factor

R is gas constant

T is temperature and

E_{a} is the activation energy


Question 4.8 In pseudo first order hydrolysis of ester in water, the following results were obtained:

15947445359861594744535593

(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.

Answer :

The average rate of reaction between the time 30 s to 60 s is expressed as-

R = \frac{d[ester]}{dt}

\\=(0.31-0.17)/60-30\\ =0.14/30=4.67\times 10^{-3} mol\ L^{-}\ s^{-}

Question 4.9(i) A reaction is first order in A and second order in B.

(i)Write the differential rate equation.

Answer :

the reaction is first order in A and second order in B. it means the power of A is one and power of B is 2

The differential rate equation will be-

-\frac{d[R]}{dt}=k[A][B]^{2}

Question 4.9(ii) A reaction is first order in A and second order in B.

(ii) How is the rate affected on increasing the concentration of B three times?

Answer :

If the concentration of [B] is increased by 3 times, then

-\frac{d[R]}{dt}=k[A][3B]^{2}

=9k[A][B]^{2}

Therefore, the rate of reaction will increase 9 times.

Question 4.9(iii) A reaction is first order in A and second order in B.

(iii) How is the rate affected when the concentrations of both A and B are doubled?

Answer :

If the concentration of [A] and[B] is increased by 2 times, then

-\frac{d[R]}{dt}=k[2A][2B]^{2}

=8k[A][B]^{2}

Therefore, the rate of reaction will increase 8 times.

Question 4.10 In a reaction between A and B, the initial rate of reaction (r0) was measure for different initial concentrations of A and B as given below:

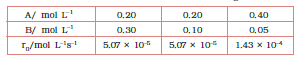
1649395389830

What is the order of the reaction with respect to A and B?

Answer :

we know that
rate law ( r_{0} ) = k[A]^{x}[B]^{y}
As per data

\\5.07\times 10^{-5} =k[0.2]^{x}[0.3]^{y}\\ 5.07\times 10^{-5}=k[0.2]^{x}[0.1]^{y}\\ 1.43\times 10^{-4}=k[0.4]^{x}[0.05]^{y} these are the equation 1, 2 and 3 respectively

Now, divide eq.1 by equation2, we get
1= (0.3/0.1)^{y}
from here we calculate that y = 0

Again, divide eq. 2 by Eq. 3, we get
Since y =0 also substitute the value of y
So,
= (\frac{1.43}{0.507})= (\frac{0.4}{0.2})^{x}
= 2.821=2^{x}

taking log both side we get,

x = \frac{\log2.821}{\log2}
= 1.496
= approx 1.5
Hence the order of reaction w.r.t A is 1.5 and w.r.t B is 0(zero)

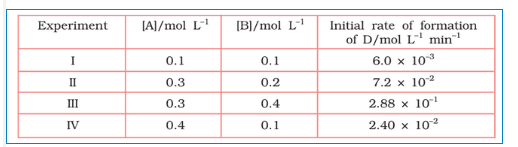
Question 4.11 The following results have been obtained during the kinetic studies of the reaction:
2A + B \rightarrow C + D

15947446824901594744682077

Determine the rate law and the rate constant for the reaction .

Answer :

Let assume the rate of reaction wrt A is x and wrt B is y . So, the rate of reaction is expressed as-
Rate = k[A]^{x}[B]^{y}

According to given data,
\\6\times 10^{-3}=k[0.1]^{x}[0.1]^{y}\\ 7.2\times 10^{-2}=k[0.3]^{x}[0.2]^{y}\\ 2.88\times 10^{-2} =k[0.3]^{x}[0.4]^{y}\\ 2.4\times 10^{-2} =k[0.4]^{x}[0.1]^{y} these are the equation 1, 2, 3 and 4 respectively

Now, divide the equation(iv) by (i) we get,
4 = (0.4/0.1)^{x}
from here we calculate that x =1

Again, divide equation (iii) by (ii)
4 =(0.4/0.2)^{y}
from here we can calculate the value of y is 2

Thus, the rate law is now, Rate = k[A][B]^{2}
So, k = rate/[A][B]^{2}
\\= 6\times 10^{-3}/(0.1)\times (0.1)^{2}\\ =6\ L^{2}\ mol^{-2}\ min^{-1}

Hence the rate constant of the reaction is =6\ L^{2}\ mol^{-2}\ min^{-1}

Question 4.12 The reaction between A and B is first order with respect to A and zero order
with respect to B. Fill in the blanks in the following table:

Experiment
[A]/molL-1
[B]/molL-1Initial rate/ mol L-1 min-1
I
0.1
0.1
2*10-2
II
-
0.2
4*10-2
III
0.4
0.4
-
IV

0.2
2*10-2

Answer :

The given reaction is first order wrt A and zero order in wrt B. So, the rate of reaction can be expressed as;
Rate = k[A][B]^{0}
Rate = k[A]

from exp 1,
2\times 10^{-2}=k(0.1)
k = 0.2 per min.

from experiment 2nd,
4\times 10^{-2}=0.2[A] \\
[A] = 0.2\ mol/L

from experiment 3rd,
rate =(0.2\ min^{-1})\times (0.4\ mol/L)
= 0.08\ mol\ L^{-1}\ min^{-1}

from the experiment 4th,

2\times 10^{-2}=0.2*[A]
from here [A] = 0.1 mol/L

Question 4.13 (1) Calculate the half-life of a first order reaction from their rate constants given below:
200 s^{-1}

Answer :

We know that,
half-life ( t_{1/2} ) for first-order reaction = 0.693/k
= 0.693/200
\approx 3.4\times 10^{-3}s

Question 4.13 (2) Calculate the half-life of a first order reaction from their rate constants given below:
2\: \: min ^{-1}

Answer :

the half-life for the first-order reaction is expressed as ;


t_{1/2}=0.693/k
= 0.693/2
= 0.35 min (approx)

Question 4.13 (3) Calculate the half-life of a first order reaction from their rate constants given below:
4 years ^{-1}

Answer :

The half-life for the first-order reaction is t_{1/2}= 0.693/k
= 0.693/4
= 0.173 year (approximately)

Question 4.14 The half-life for radioactive decay of ^{14} C is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.

Answer :

Given ,
half-life of radioactive decay = 5730 years
So, t_{1/2}= 0.693/k
k = 0.693/5730 per year

we know that, for first-order reaction,
t = \frac{2.303}{k} \log\frac{[R_{0}]}{[R]}
t = \frac{2.303}{.693/5730} \log\frac{100}{80}
= 1845 years (approximately)

Thus, the age of the sample is 1845 years

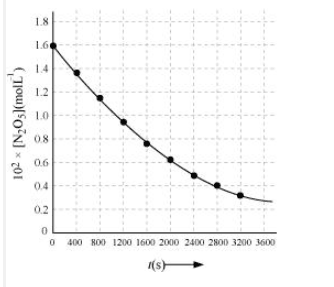
Question 4.15 (1) The experimental data for decomposition of

2 N_2 O_5 \rightarrow 4 NO_2 + O_2
in gas phase at 318K are given below:

15947447560991594744755760

Plot [N_2O_5] against t.

Answer :

On increasing time, the concentration of N_{2}O_{5} gradually decreasing exponentially.

15947448924751594744892159

Question 4.15 (2) The experimental data for decomposition of 2 N_2O_5 \rightarrow 4 NO_2 + O_2 in gas phase at 318K are given below:

15947447789591594744778214

Find the half-life period for the reaction.

Answer :

The half-life of the reaction is-
The time corresponding to the 1.63 \times 10^{2}/2 mol/ L = 81.5 mol /L is the half-life of the reaction. From the graph, the answer should be in the range of 1400 s to 1500 s.


Question 4.15 (3) The experimental data for decomposition of N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2] in gas phase at 318K are given below:

15947449836811594744983358

Draw a graph between \log [ N_2 O_5 ] and t.

Answer :

t/S 10^{2}\times [N_{2}O_{5}] \log[N_{2}O_{5}]
0 1.63 -1.79
400 1.36 -1.87
800 1.14 -1.94
1200 0.93 -2.03
1600 0.78 -2.11
2000 0.64 -2.19
2400 0.53 -2.28
2800 0.43 -2.37
3200 0.35 -2.46


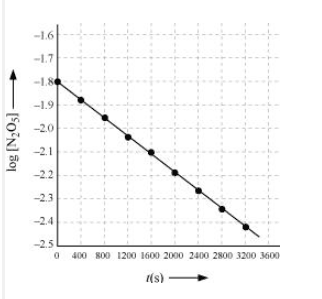
15947454706271594745470023


Question 4.15 (4) The experimental data for decomposition of N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2] in gas phase at 318K are given below:

15947448045441594744803921

What is the rate law ?

Answer :

Here, the reaction is in first order reaction because its log graph is linear.
Thus rate law can be expessed as Rate = k[N_{2}O_{5}]

Question 4.15 (5) The experimental data for decomposition of N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2] in gas phase at 318K are given below:

15947448152801594744814878

Calculate the rate constant.

Answer :

From the log graph,

the slope of the graph is = \frac{-2.46-1.79}{3200}
= -k/2.303 ..(from log equation)

On comparing both the equation we get,

-k/2.303 = -0.67/3200
k= 3200\times (0.67/3200)
k= 4.82 \times 10^{-4}\ s^{-1}

Question 4.15 (6) The experimental data for decomposition of N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2] in gas phase at 318K are given below:

15947448318061594744831445

Calculate the half-life period from k and compare it with (ii).

Answer :

The half life produce = 0.693/k
= =0.693/4.82 \times 10^{-4}
1.438\times 10^{3} s

Question 4.15(7) The rate constant for a first order reaction is 60 s^{-1} . How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?

Answer :

We know that,
for first order reaction,
t=\frac{2.303}{k}\log\frac{[R]_{0}}{[R]}
\\=\frac{2.303}{60}\log\frac{1}{1/16}\\ =\frac{2.303}{60} \log2^{4}
=4.6 \times 10^{-2} s (nearly)

Hence the time required is =4.6 \times 10^{-2} s

Question 4.17 During nuclear explosion, one of the products is ^{90} Sr with half-life of 28.1 years. If 1 \mu g of ^{90}Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.

Answer :

Given,
half life = 21.8 years
\therefore\ k=0.693/t_{1/2}
= 0.693/21.8

and, t = \frac{2.303}{k}\log\frac{[R]_{0}}{[R]}

by putting the value we get,

10= \frac{2.303}{0.693/21.8}\log\frac{1}{[R]}
\log[R] = -\frac{10\times 0.693}{2.303\times 21.8}
taking antilog on both sides,
[R] = antilog(-0.1071)
= 0.781 \mu g

Thus 0.781 \mu g of {Sr}^{90} will remain after given 10 years of time.

Again,

15947450926031594745092246
Thus 0.2278 \mu g of {Sr}^{90} will remain after 60 years.

Question 4.18 For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.

Answer :

case 1-

for 99% complition,
t^{1} = \frac{2.303}{k}\log\frac{100}{100-99}
= \frac{2.303}{k}\log100
=2\times (\frac{2.303}{k})

CASE- II
for 90% complition,

t^{2}=\frac{2.303}{k}\log\frac{100}{100-90}
=\frac{2.303}{k}\log10
=(\frac{t^{1}}{2})

t^{1}=2t^{2}
Hence proved.

Question 4.19 A first order reaction takes 40 min for 30% decomposition. Calculate t_{1/2}

Answer :

For the first-order reaction,

t =\frac{2.303}{k}\log \frac{[R]_{0}}{[R]}
k =\frac{2.303}{40}\log \frac{100}{100-30} (30% already decomposed and remaining is 70%)

=8.918\times 10^{-3} min^{-1}

therefore half life = 0.693/k
= 0.693/8.918\times 10^{-3}
= 77.7 (approx)

Question 4.20 For the decomposition of azoisopropane to hexane and nitrogen at 543K, the following data are obtained.

15947455515361594745548735

Calculate the rate constant.

Answer :

Decomposition is represented by equation-

15947457413321594745740908
After t time, the total pressure p_{T} = p_{0}-p+(p+p) = p_{0}+p

So, p = p_{t}-p_{0}

thus, p_{0}-p = 2p_{0}-p_{t}

for first order reaction,

k= \frac{2.303}{t}\log\frac{p_{0}}{p_{0}-p}
= \frac{2.303}{360}\log\frac{p_{0}}{2p_{0}-p_{t}}
now putting the values of pressures,

when t =360sec

= \frac{2.303}{360}\log\frac{35}{2*35-54}
= 2.175\times 10^{-3}s^{-1}

when t = 270sec

= \frac{2.303}{270}\log\frac{35}{2*35-54}
= 2.235\times 10^{-3}s^{-1}

So, k_{avg}=k_{1}+k_{2}/2
=2.21\times 10^{-3}\ s^{-1}

Question 4.21 The following data were obtained during the first order thermal decomposition of SO_2 Cl_2 at a constant volume.
( SO_2Cl_2 g) \rightarrow SO_2 (g) + Cl_2 (g)

15947452128701594745210169

Calculate the rate of the reaction when total pressure is 0.65 atm.

Answer :

The thermal decomposition of SO_{2}Cl_{2} is shown here;
15947452231641594745222570

After t time, the total pressure p_{t} = p_{0}-p+(p+p) = p_{0}+p

So, p = p_{t}-p_{0}

thus, p_{0}-p = 2p_{0}-p_{t}

for first order reaction,

k= \frac{2.303}{t}\log\frac{p_{0}}{p_{0}-p}
= \frac{2.303}{360}\log\frac{p_{0}}{2p_{0}-p_{t}}
now putting the values of pressures, when t = 100s
k = \frac{2.303}{100}\log\frac{0.5}{2*0.5-0.6}
= 2.231 \times 10^{-3}\ s^{-1}

when p_{t} = 0.65\ atm

p = p_{t}-p_{0}
= 0.65 - 0.5
= 0.15 atm

So, p(_{SO_{2}Cl_{2}}) = p_{0}-p
= 0.5 - 0.15
= 0.35 atm

Thus, rate of reaction, when the total pressure is 0.65 atm
rate = k( p(_{SO_{2}Cl_{2}}) )
= 2.31\times 10^{-3}\times 0.35
= 7.8 \times 10^{-4}\ atm\ s^{-1}

Question 4.22 The rate constant for the decomposition of N2O5 at various temperatures
is given below:

15947452429101594745242519

Draw a graph between ln k and 1/T and calculate the values of A and
E_a . Predict the rate constant at 30° and 50°C.

Answer :

From the above data,

T/ C^{0} 0 20 40 60 80
T/K 273 293 313 333 353
1/T / K^{-1} ( \times 10^{-3} ) 3.66 3.41 3.19 3.0 2.83
10^{5}*K/S^{-} 0.0787 1.70 25.7 178 2140
ln\ K -7.147 -4.075 -1.359 -0.577 3.063

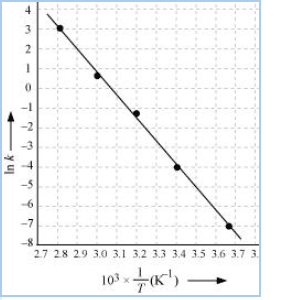
15947452580691594745257653
Slope of line = \frac{y2-y2}{x2-x1} = -12.30\ K

According to Arrhenius equations,

Slope = -E_{a}/R
E_{a}= 12.30 \times 8.314
= 102.27 KJ mol^{-1}

Again,
15947452776351594745277231
When T = 30 +273 = 303 K and 1/T =0.0033K
\ln k= -2.8

\therefore k = 6.08\times 10^{-2}\ s^{-1}

When T = 50 + 273 = 323 K and 1/T = 3.1 \times 10^{-3} K
\ln k = -0.5
\therefore k = 0.607 per sec

Question 4.23 The rate constant for the decomposition of hydrocarbons is 2.418 \times 10 ^{-5} s ^{-1} at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor.

Answer :

Given that,
k = 2.418 \times 10 ^{-5} s ^{-1}
E_{a} = 179.9 KJ/mol
T(temp) = 546K

According to Arrhenius equation,

k=Ae^{-E_{a}/RT}
taking log on both sides,
\log k = \log A - \frac{E_{a}}{2.303 RT}

\log A =\log k + \frac{E_{a}}{2.303 RT}

=\log (2.418\times 10^{-5}) + \frac{179.9\times 10^{3}}{2.303 \times 8.314 \times 546}

= (0.3835 - 5) + 17.2082
= 12.5917
Thus A = antilog (12.5917)
A = 3.9 \times 10^{12} per sec (approx)

Question 4.24 Consider a certain reaction A \rightarrow Products with k = 2.0 \times 10 ^{-2 } s ^{-1} . Calculatethe concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L^{-1}

Answer :

Given that,
k = =2\times 10^{-2}
t = 100 s
[A]_0= 1\ mol\ L^{-1}
Here the unit of k is in per sec, it means it is a first-order reaction.
therefore,
k = \frac{2.303}{t}\log\frac{[A]_o}{[A]}
\\2\times 10^{-2} = \frac{2.303}{100}\log\frac{1}{[A]}\\ 2\times 10^{-2} = -\frac{2.303}{100}\log[A]\\ \log[A]=-\frac{2}{2.303}\\
\\A = anti\log\frac{-2}{2.303}\\ A= 0.135 mol\ L^{-1}

Hence the concentration of rest test sample is 0.135 mol/L

Question 4.25 Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t _{1/2 } = 3.00 hours. What fraction of sample of sucrose remains after 8 hours ?

Answer :

For first order reaction,

k = \frac{2.303}{t}\log\frac{[R]_{0}}{[R]}

given that half life = 3 hrs ( t_{1/2} )

Therefore k = 0.693/half-life
= 0.231 per hour

Now,

\\0.231 = \frac{2.303}{8}\log\frac{[R]_{0}}{[R]}\\ \log\frac{[R]_{0}}{[R]} = 0.231\times \frac{8}{2.203}
= antilog (0.8024)
= 6.3445

[R]_{0}/[R] = 6.3445

[R]/[R]_{0} = 0.157 (approx)

Therefore fraction of sample of sucrose remains after 8 hrs is 0.157

Question 4.26 The decomposition of hydrocarbon follows the equation k=(4.51011s-1)e-28000K/T . Calculate E_{a}

Answer :

The Arrhenius equation is given by
k=Ae^{-E_{a}/RT} .................................(i)
given equation,
k = (4.5 × 1011s^{-1}) e^{-28000K/T} ............................(ii)

by comparing equation (i) & (ii) we get,

A= 4.51011 per sec
E_{a}/RT =28000/T
Activation energy = 28000 \times (R = 8.314)
= 232.792 KJ/mol

Question 4.27 The rate constant for the first order decomposition of H_2O_2 is given by the following equation:
\log k = 14.34 - 1.25 \times 10 ^ 4K/T .

Calculate E_a for this reaction and at what temperature will its half-period be 256 minutes?

Answer :

The Arrhenius equation is given by
k=Ae^{-E_{a}/RT}

taking log on both sides,

\log k = \log A -\frac{E_{a}}{2.303RT} ....................(i)
given equation,

\log k = 14.34 - 1.25 \times 10 ^ 4K/T .....................(ii)

On comparing both equation we get,

E_{a}/2.303R=1.25 \times 10^{4}

activation energy
\\=1.25 \times 10^{4} \times 2.303 \times 8.314\\ =239.34\ KJ/mol

half life ( t_{1/2} ) = 256 min

k = 0.693/256
k = 4.51\times 10^{-5} s^{-1}

With the help of equation (ii),

\log4.51\times 10^{-5} s^{-1} = 14.34-\frac{1.25\times 10^{4}}{T}

\frac{1.25\times 10^{4}}{T} = 18.686
T = \frac{1.25\times 10^{4}}{18.686}

= 669 (approx)

Question 4.28 The decomposition of A into product has value of k as 4.5 \times 10 ^3 s ^{-1} at 10°Cand energy of activation 60 kJ mol–1. At what temperature would k be 1.5 \times 10 ^4 s ^{-1} ?

Answer :

The decomposition of A into a product has a value of k as 4.5 \times 10 ^3 s ^{-1} at 10°C and energy of activation 60 kJ mol–1.

K1 = 4.5 \times 10 ^3 s ^{-1}
K2 = 1.5 \times 10 ^4 s ^{-1}

E_a = 60 kJ mol–1

K2 = 1.5 \times 10 ^4 s ^{-1}

log\frac{K_2}{K_1}=\frac{E_a(T_2-T_1)}{2.303RT_1T_2}

log(\frac{1.5\times 10^{4}}{4.5\times 10^{3}})=\frac{60(T_2-283)}{2.303\times R\times 283\times T_2}

log(\frac{150}{45})=\frac{60(T_2-283)}{5418.61\times T_2}

log150-log45=\frac{60T_2-16980}{5418.61\times T_2}

2.176-1.653=\frac{60T_2-16980}{5418.61\times T_2}

0.5229=\frac{60T_2-16980}{5418.61\times T_2}

T_2=\frac{16980}{2733.4}

T_2=6.1K

Question 4.29 The time required for 10% completion of a first order reaction at 298K is equal to that required for its 25% completion at 308K. If the value of A is 4 \times 10 ^{10} s ^{-1} . Calculate k at 318K and Ea.

Answer :

We know that,

for a first order reaction-

t = \frac{2.303}{k}\log\frac{a}{a-x}

Case 1
At temp. = 298 K
t = \frac{2.303}{k}\log\frac{100}{90}
= 0.1054/k

Case 2
At temp = 308 K

t' = \frac{2.303}{k}\log\frac{100}{75}
= 2.2877/k'
As per the question
t' = t
K'/K = 2.7296

From Arrhenius equation,

15947453267681594745326105
= 76640.096 J /mol
=76.64 KJ/mol


k at 318 K
we have , T =318K
A= 4 \times 10^{10}

Now \log k = \log A- \frac{E_{a}}{2.303RT}
After putting the calue of given variable, we get

\log k = -1.9855
on takingantilog we get,

k = antilog(-1.9855)

= 1.034 \times 10^{-2}\ s^{-1}

Question 4.30 The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.

Answer :

From the Arrhenius equation,

\log\frac{k_{2}}{k_{1}}=\frac{E_{a}}{2.303R}(\frac{T_{2}-T_{1}}{T_{1}T_{2}}) ...................................(i)
it is given that k_{2}=4k_{1}
T1= 293 K

T2 = 313 K
Putting all these values in equation (i) we get,

\log 4 =\frac{E_{a}}{2.303 \times 8.314}(\frac{313-293}{313 \times 293})

15947453794861594745378630

Activation Energy = 52.86 KJ/mo l
This is the required activation energy

Topics and Sub-topics of Chemical Kinetics Class 12 NCERT Chapter 4

  • 4.1 Rate of a Chemical Reaction
  • 4.2 Factors Influencing Rate of a Reaction
  • 4.3 Integrated Rate Equations
  • 4.4 Temperature Dependence of the Rate of a Reaction
  • 4.5 Collision Theory of Chemical Reactions
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

NCERT Chapter-wise Solutions for Class 12 Chemistry

More About Class 12 Chemistry Chapter 4 Chemical Kinetics NCERT solutions

  • A total of 5 marks of questions will be asked in the Class 12 CBSE board exam of Chemistry from this chapter.

  • In this chapter, there are 30 questions in the exercise and 9 questions that are related to topics studied.

  • To clear doubts of students, the Chemical Kinetics NCERT solutions are prepared in a comprehensive manner by subject experts.

  • This chapter is vital for both CBSE Board exam as well as for competitive exams like JEE Mains, VITEEE, BITSAT, etc. so, students must pay special attention to the concepts of this chapter.

  • The NCERT solutions provided here are completely free and you can also download them for offline use also if you want to prepare or any other subject or any other class.

  • By referring to the NCERT Solutions for Class 12 chemistry chapter 4 PDF download, students can understand all the important concepts and practice questions well enough before their examination.

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

NCERT Solutions for Class 12 Subject wise

Benefits of NCERT solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics

  • First, the easy steps given in the NCERT Class 12 Chemistry solutions chapter 4 will help you to understand the chapter easily.

  • The revision will be so easy that you always remember the concepts and get very good marks in your class.

  • Homework will be easy now, all you need to do is check the detailed CBSE NCERT solutions for class 12 chemistry chapter 4 Chemical Kinetics and you are good to go.

  • If you have a doubt or question that is not available here or in any of the chapters, contact us. You will get the answers with solutions that will help you score well in your exams.

Also check NCERT Exemplar Class 12 Solutions

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Questions (FAQs)

1. What are the important topics of this chapter?

Important topics of this chemical kinetics are the rate of reaction, concept of collision theory, effect of temperature in activation energy, Arrhenius equation, concept of collision theory.

2. What is the weightage of NCERT class 12 Chemistry chapter 4 in CBSE board exam?

The weightage of NCERT class 12 Chemistry chapter 4 in CBSE board exam is 5 marks. To practice questions on the chapter refer to NCERT book exercise and NCERT exemplar problems.

3. What is the weightage of NCERT class 12 Chemistry chapter 4 in NEET?

The weightage of NCERT class 12 Chemistry chapter 4 in NEET is 3%. Solve more previous year NEET papers to get more problems

4. What is the weightage of NCERT class 12 Chemistry chapter 4 in JEE Mains?

Weightage of NCERT class 12 Chemistry chapter 4 in JEE Mains is 4 marks.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Gujarat Board Secondary School Certificate Examination

Late Fee Application Date:11 December,2024 - 20 December,2024

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Business Analytics Foundations
 Via PW Skills
Digital Banking Business Model
 Via State Bank of India
Full-Stack Android Development
 Via Masai School
Data Science for Beginners
 Via Board Infinity
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Board Exams: States agree to equivalence; no question paper ‘jumbling’ from next year, says PARAKH CEO
December 12, 2024 - 12:44 PM IST
Board Exam Date 2025 Live: CBSE, ICSE, BSEB, MPBSE Class 10, 12 timetable out; Punjab, Rajasthan schedule soon
December 08, 2024 - 10:34 PM IST
CBSE Board Exams 2025: Guidelines issued for Class 10, 12 practicals
December 03, 2024 - 01:11 PM IST
Board Exam Date Sheet 2025 Live: ICSE, ISC, CBSE, MP time table out; BSEB routine soon
November 26, 2024 - 10:18 PM IST
Board exam dates 2025: CBSE, CISCE, UP, MP, Maharashtra, TN time table out; state-wise updates
November 25, 2024 - 08:42 PM IST
Board Exam Date Sheet 2025: CBSE, UPMSP, MPBSE, Class 10, 12 board exam dates out; BSEB, CGBSE schedules soon
November 22, 2024 - 10:04 PM IST
CBSE Date Sheet 2025 (Out) Live: Class 10, 12 board exam time table at cbse.gov.in; syllabus, sample papers
November 21, 2024 - 09:30 PM IST

Stay up-to date with CBSE Class 12th News

Back to top