NCERT Solutions for Class 11 Physics Chapter 7 Gravitation
Have you ever thought why does an apple fall on the ground, but the Moon never hits the Earth? Or how do the planets remain in their orbits? The solution is in the universal force of gravitation. This phenomenon of nature not only draws all objects towards the earth but also determines the movement of heavenly bodies in the world. When it comes to a mere act such as walking uphill or downhill, the effect of gravity is felt.
This Story also Contains
- NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation: Download PDF
- NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation: Exercise Questions
- NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation: Additional Questions
- Class 11 Physics Chapter 7 - Gravitation: Higher Order Thinking Skills (HOTS) Questions
- Class 11 Physics Chapter 7 - Gravitation: Topics
- Class 11 Physics Chapter 7 - Gravitation question answers: Important Formulae
- How Can NCERT Solutions for Class 11 Physics Chapter 7 Help in Exam Preparation?
- Approach to Solve Questions of Class 11 Physics Chapter 7 - Gravitation
- Importance of NCERT Solutions for Class 11 Physics Chapter 7: Gravitation
- What Students Learn from NCERT Solutions for Class 11 Physics Chapter 7: Gravitation?
- What Extra Should Students Study Beyond the NCERT for JEE/NEET?
- NCERT Solutions for Class 11 Physics Chapter-Wise

Chapter 7 - Gravitation of the Class 11 Physics NCERT syllabus is among the most important chapters because it covers the laws of attraction of bodies and the Earth. In order to simplify the learning process, NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation are presented in a detailed step-by-step format with answers to all the text questions, as well as a clear explanation of the formulae and derivations. These NCERT solutions include all major concepts like Kepler Laws of Planetary Motion, Acceleration due to Gravity, the Varying g and Gravitational Potential Energy. They are not only very helpful in CBSE board exams, but also in competitive exams such as JEE and NEET. Through these NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation, students are able to reinforce their conceptual knowledge, enhance their accuracy in numerical problems and improve their performance in exams.
NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation: Download PDF
Gravitation, the key force that provides the structure of the universe, the motion of the planets and the tides, is discussed in Chapter 7 of Class 11 of the subject Physics. The Class 11 Physics Chapter 7 - Gravitation question answers also elaborate major concepts such as the Newton Law of Gravitation, the acceleration due to gravity and the motion of the satellite. The PDF can also be downloaded to give step-by-step solutions to improve their knowledge and examination results.
NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation: Exercise Questions
Gravitation Chapter 7 in Class 11 Physics is about the universal law of gravitation, planetary motions, variations of gravity, and the manner in which this is used numerically. The Gravitation class 11 question answers also give step-by-step solutions to ensure that students learn the theory and numerical concepts in an easy manner. These are solutions that are prepared by experts to help enhance problem-solving abilities, and they are very helpful in both CBSE exams and also in competitive exams like JEE and NEET.
Q: 7.1 (a) Answer the following questions:
Answer:
No, because gravitational force doesn't depend upon the material medium. It is independent of the presence of other materials.
Q: 7.1 (b) Answer the following :
Answer:
Yes, if the size of the space station is large, then he can detect gravity.
Q: 7.1 (c) Answer the following:
Answer:
Apart from the gravitational pull, the tidal effect also depends on the cube of the distance between the two. Since the distance between Earth and the sun is much larger than the distance between the sun and the moon so it also does not balance but is more than the effect of gravitational force. Thus, the tidal effect of the moon’s pull is greater than the tidal effect of the sun.
Q: 7.2 Choose the correct alternative :
(a) Acceleration due to gravity increases/decreases with increasing altitude.
(c) Acceleration due to gravity is independent of the mass of the Earth/mass of the body.
Answer:
(a) Acceleration due to gravity decreases with increasing altitude.
The relation between the two is given by :
$g_h\ =\ \left ( 1\ -\ \frac{2h}{R_e} \right )g$
(b) Acceleration due to gravity decreases with increasing depth.
The relation is given below:
$g_d\ =\ \left ( 1\ -\ \frac{d}{R_e} \right )g$
(c) Acceleration due to gravity is independent of the mass of the body.
$g\ =\ \frac{GM}{R^2}$ Here M is the mass of the earth.
(d) The formula $-G M m\left(1 / r_2-1 / r_1\right)$ is more accurate than the formula $m g\left(r_2-r_1\right)$ for the difference of potential energy between two points $r_2$ and $r_1$ distance away from the centre of the earth.
Answer:
Time taken by planet to complete a revolution around sun = $\frac{1}{2}T_e$
Using Kepler's law of planetary motion, we can write :
$\left ( \frac{R_p}{R_e} \right )^3\ =\ \left ( \frac{T_p}{T_e} \right )^2$
or $\frac{R_p}{R_e}\ =\ \left ( \frac{\frac{1}{2}}{1} \right )^\frac{2}{3}$
or $\frac{R_p}{R_e}\ =\ 0.63$
Thus, the planet is 0.63 times smaller than Earth.
Answer:
The orbital period in days is $=\ 1.769\times 24 \times 60\times 60\ s$
Mass is given by :
$M\ =\ \frac{4 \pi ^2 R^3}{GT^2}$
Thus, the ratio of the mass of Jupiter and the mass of the sun is :
$\frac{M_s}{M_j} =\ \frac{\frac{4 \pi ^2 R_e^3}{GT_e^2}}{\frac{4 \pi ^2 R_{io}^3}{GT_{io}^2}}$
or $\frac{M_s}{M_j}=\ \left ( \frac{1.769 \times 24\times 60\times 60}{365.25\times 24\times 60\times 60} \right )^2\times \left ( \frac{1.496\times 10^{11}}{4.22\times 10^8} \right )^3$
or $\frac{M_s}{M_j}\approx 1045$
Thus, the mass of Jupiter is nearly one-thousandth that of the sun.
Answer:
We know that one light year is $9.45\times 10^{15}\ m$.
The time period of rotation is given by :
$T\ =\ \left ( \frac{4 \pi r^3}{GM} \right )^\frac{1}{2}$
Putting all the values (in SI units) in the above equation, we get :
$T=\ \left ( \frac{4 \times \left ( 3.14 \right )^2\times (4.73)^3\times 10^{60}}{6.67\times 10^{-11} \times 5\times 10^{41}} \right )^\frac{1}{2}$
or $T=\ 1.12\ \times 10^{16}\ s$
In years :
$T=\ \frac{1.12\ \times 10^{16}}{365 \times 24 \times 60 \times 60}\ =\ 3.55\times 10^8\ years$
Q: 7.6 Choose the correct alternative:
Answer:
(a) The total energy will be negative of its kinetic energy. Since at infinity, potential energy is zero, and total energy is negative.
(b) The energy required will be less as the stationary object on earth has no energy initially, whereas the satellite has gained energy due to rotational motion.
Answer:
The escape velocity from the Earth is given by :
$v_{esc}\ =\ \sqrt{2gR}$
Since the escape velocity depends upon the reference (potential energy), it only depends upon the height of the location.
(a) No
(b) No
(c) No
(d) Yes
Answer:
Among all, only the angular momentum and total energy of the comet will be constant; all other factors given will vary from point to point.
Answer:
(a) In space, we have a state of weightlessness, so the swollen feet do not affect astronauts, as there is no gravitational pull (so they cannot stand).
(b) The swollen face will be affected as the sense organs, such as eyes, ears, etc., will be affected.
(c) It will affect the astronaut as it may cause mental strain.
(d) It will affect the astronaut as space has different orientations.
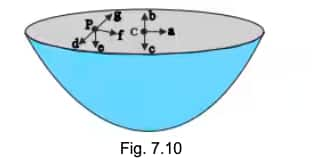
Answer:
We know that the gravitational potential (V) in a sphere is constant throughout. Also, the gravitational intensity will act in the downward direction as its upper half is cut (gravitational force will also act in a downward direction). Hence, the required direction of gravitational intensity is shown by arrow c.
.png)
Answer:
As stated in the previous question, the gravitational potential in a spherical shell is constant throughout. So the gravitational intensity will act in the downward direction (as the upper half is cut). So the required direction is shown by arrow e.
Answer:
Let the distance where the gravitational force acting on satellite P becomes zero be x from the earth.
Thus, we can write :
$\frac{GmM_s}{(r-x)^2}\ =\ \frac{GmM_e}{r^2}$
or $\left ( \frac{r-x}{x} \right )\ =\ \left ( \frac{2\times 10^{30}}{60\times 10^{24}} \right )^\frac{1}{2}$
or $\left ( \frac{r-x}{x} \right )=\ 577.35$
Hence :
$x\ =\ \frac{1.5\times 10^{11}}{578.35}\ =\ 2.59\times 10^8\ m$ (Since r = $1.5\times 10^{11}$ )
Answer:
Mass of the Sun can be calculated by using the following formula:-
$M\ =\ \frac{4 \times \pi^2 \times r^3 }{GT^2}$
Putting the known values in the above formula, we obtain :
$M=\ \frac{4 \times (3.14)^2 \times (1.5\times 10^{11})^3 }{6.67\times 10^{-11}\times (365.25\times 24\times 60 \times 60)^2}$
or $M=\ \frac{133.24\times 10}{6.64\times 10^4}\ =\ 2\times 10^{30}\ Kg$
Thus, the mass of the sun is nearly $2\times 10^{30}\ Kg$.
Answer:
Kepler's third law gives us the following relation :
$T\ =\ \left ( \frac{ \pi^2 r^3}{GM} \right )^ \frac{1}{2}$
Thus, we can write :
$\frac{r_s^3}{r_e^3}\ =\ \frac{T_s^2}{T_e^2}$
or $r_s\ =\ r_e\left ( \frac{T_s}{T_e} \right )^ \frac{2}{3}$
or $r_s=\ 1.5 \times 10^{11}\times \left ( \frac{29.5 T_e}{T_e} \right )^ \frac{2}{3}$
or $r_s=\ 14.32 \times 10^{11}\ m$
Thus, the distance between the sun and Saturn is $14.32 \times 10^{11}\ m$.
Answer:
Acceleration due to gravity at height h from the surface of Earth is :
$g'\ =\ \frac {g}{\left ( 1\ +\ \frac{h}{R} \right )^2}$
For $h\ =\ \frac{R}{2}$ we have :
$g'\ =\ \frac {g}{\left ( 1\ +\ \frac{\frac{R}{2}}{R} \right )^2}$
or $g'=\ \frac{4}{9}g$
Thus, the weight of the body will be :
$W\ =\ mg'$
or $W=\ m\times \frac{4}{9}g\ =\ \frac{4}{9}mg$
or $W=\ 28\ N$
Answer:
Position of the body is (depth) :
$=\ \frac{1}{2}R_e$
Acceleration due to gravity at depth d is given by :
$g'\ =\ \left ( 1\ -\ \frac{d}{R_e} \right )g$
or $g'=\ \left ( 1\ -\ \frac{\frac{R_e}{2}}{R_e} \right )g$
or $g'=\ \frac{1}{2}g$
Thus, the weight of the body is:-
$W\ =\ mg'$
or $W=\ m\times \frac{1}{2}g\ =\ \frac{mg}{2}$
or $W=\ 125\ N$
Thus, the weight of the body is 125 N.
Answer:
The total energy is given by :
Total energy = Potential energy + Kinetic energy
$=\ \left ( \frac{ -GmM_e}{R_e} \right )\ +\ \frac{1}{2}mv^2$
At the highest point, velocity will be zero.
Thu,s the total energy of the rocket is :
$=\ \left ( \frac{ -GmM_e}{R_e\ +\ h} \right )\ +\ 0$
Now we will use the conservation of energy :
Total energy initially (at Earth's surface) = Total energy at height h
$\left ( \frac{ -GmM_e}{R_e} \right )\ +\ \frac{1}{2}mv^2\ =\ \left ( \frac{ -GmM_e}{R_e\ +\ h} \right )$
or $\frac{1}{2}v^2\ =\ \frac{ gR_eh}{R_e\ +\ h}$
or $h\ =\ \frac{R_e v^2}{2gR_e\ -\ v^2}$
or $h=\ \frac{6.4\times 10^{6}\times (5\times 10^3)^2}{2g\times 6.4\times 10^6\ -\ (5\times 10^3)^2}$
or $h=\ 1.6\times 10^6\ m$
Hence, the height achieved by the rocket from Earth's centre = R + h
$R+h=\ 6.4\times 10^6\ +\ 1.6 \times 10^6$
or $R+h=\ 8\times 10^6\ m$
Answer:
Let us assume the speed of the body far away from the earth is $v_f$.
Total energy on Earth is :
$=\ \frac{1}{2}mv_p^2\ -\ \frac{1}{2}mv_{esc}^2$
And the total energy when the body is far from the earth is :
$=\ \frac{1}{2}mv_f^2$
(Since the potential energy far from the earth is zero.)
We will use conservation of energy: -
$\frac{1}{2}mv_p^2\ -\ \frac{1}{2}mv_{esc}^2\ =\ \frac{1}{2}mv_f^2$
or $v_f\ =\ \sqrt{\left ( v_p^2\ -\ v_{esc}^2 \right )}$
or $v_f=\ \sqrt{\left ( \left ( 3v_{esc} \right )^2\ -\ v_{esc}^2 \right )}$
or $v_f=\ \sqrt{8}v_{esc}$
or $v_f=\ 31.68\ km/s$
Answer:
The total energy of the satellite at height h is given by :
$=\ \frac{1}{2}mv^2\ +\ \left ( \frac{-GM_em}{R_e\ +\ h} \right )$
We know that the orbital speed of the satellite is :
$v\ =\ \sqrt{\left ( \frac{GM_e}{R_e\ +\ h} \right )}$
Thus, the total energy becomes :
$E=\ \frac{1}{2}m\times \left ( \frac{GM_e}{R_e\ +\ h} \right )\ +\ \left ( \frac{-GM_em}{R_e\ +\ h} \right )$
or $E=\ - \frac{1}{2} \left ( \frac{GM_em}{R_e\ +\ h} \right )$
Thus, the required energy is the negative of the total energy :
nbsp; $E_{req}\ =\ \frac{1}{2} \left ( \frac{GM_em}{R_e\ +\ h} \right )$
or $E_{req}=\ \frac{1}{2} \left ( \frac{6.67\times 10^{-11}\times 6 \times 10^{24}\times 200}{6.4\times 10^6\ +\ 0.4\times 10^6} \right )$
or $E_{req}=\ 5.9\times 10^9\ J$
Answer:
The total energy of stars is given by :
$E\ =\ \frac{-GMM}{r}\ +\ \frac{1}{2}Mv^2$
or $E=\ \frac{-GMM}{r}\ +\ 0$
or $E=\ \frac{-GMM}{r}$
Now, when stars are just about to collide, the distance between them is 2R.
The total kinetic energy of both stars is :
$KE=\ \frac{1}{2}Mv^2\ +\ \frac{1}{2}Mv^2\ =\ Mv^2$
And the total energy of both the stars is :
$E'=\ Mv^2\ +\ \frac{-GMM}{2r}$
Using conservation of energy, we get :
$Mv^2\ +\ \frac{-GMM}{2r}\ =\ \frac{-GMM}{r}$
or $v^2\ =\ GM \left ( \frac{-1}{r}\ +\ \frac{1}{2R} \right )$
or $v^2=\ 6.67\times 10^{-11}\times 2\times 10^{30} \left ( \frac{-1}{10^{12}}\ +\ \frac{1}{2\times 10^7} \right )$
or $v^2=\ 6.67\times 10^{12}$
Thus the velocity is : $\sqrt{6.67\times 10^{12}}\ =\ 2.58\times 10^6\ m/s$
Answer:
The gravitational force at the midpoint will be zero. This is because both spheres are identical, and their forces will be equal but opposite in direction.
The gravitational potential is given by :
$=\ \frac {-GM}{\frac{r}{2}}\ -\ \frac{-GM}{\frac{r}{2}}\ =\ \frac{-4GM}{r}$
$=\ \frac{-4\times 6.67\times 10^{-11}\times 100}{1}$
$=\ -2.67\times 10^{-8}\ J/Kg$
At the midpoint, we have equal forces in opposite directions, so it is in equilibrium, but if we move the body slightly, then the particle will move in one direction (as one force will be greater). So it is an unstable equilibrium.
NCERT Solutions for Class 11 Physics Chapter 7 - Gravitation: Additional Questions
The Additional Questions of Class 11 Physics Chapter 7 - Gravitation have been framed in such a way that they are supposed to cover more than what the NCERT textbook covers and enhance the knowledge of major principles. These questions revolve around learning application-based and numerical problem-solving and critical thinking. They are very practical when it comes to practising by students who want to get a better score in their school exams and other competitive tests, such as JEE.
Answer:
Height of satellite from earth's surface: $3.6\times 10^7\ m$
Gravitational potential is given by :
$=\ \frac{-GM}{R\ +\ h}$
$=\ \frac{-6.67\times 10^{-11}\times 6\times 10^{24}}{3.6\times 10^7\ +\ 0.64\times 10^7 }$
$=\ -\ 9.4\times 10^6\ J/Kg$
Thus potential due to Earth's gravity is $-\ 9.4\times 10^6\ J/Kg$.
Answer:
A body will get stuck at the star's surface if the centrifugal force of the star is less than the gravitational force.
The gravitational force is given by :
$F_g\ =\ \frac{GMm}{r^2}$
or $F_g=\ \frac{6.67\times 10^{-11}\times 5\times 10^{30}\times m}{(1.2\times 10^4)^2}\ =\ 2.31\times 10^{12}\ m\ N$
The centrifugal force is given by :
$F_c\ =\ mr\omega ^2$
or $F_c=\ mr(2\pi v) ^2$ $=\ m\times 1.2\times 10^4\times (2\pi \times 1.2) ^2$
or $F_c=\ 6.8\times 10^5\ m\ N$
As we can see, the gravitational force is greater than the centrifugal force, thus the body will remain at the star.
Answer:
Firstly, the potential energy of the spaceship due to the sun is given by :
$=\ \frac{-GMm_s}{r}$
and the potential energy of the spaceship due to Mars is given by :
$=\ \frac{-GMm_m}{R}$
It is given that the spaceship is stationary, so its kinetic energy is zero.
Thus, the total energy of the spaceship is :
$=\ \frac{-GMm_s}{r}\ +\ \frac{-GMm_m}{R}$
Thus, the energy needed to launch the spaceship is :
$=\ \frac{GMm_s}{r}\ +\ \frac{GMm_m}{R}$
$=\ 6.67\times 10^{-11}\times 10^3 \left ( \frac{2\times 10^{30}}{2.28\times 10^{11}}\ +\ \frac{6.4\times 10^{23}}{3.395\times 10^6} \right )$
$=\ 596.97\times 10^9\ J$
$=\ 6\times 10^{11}\ J$
Answer:
The kinetic energy of the rocket is (initial):-
$=\ \frac{1}{2}mv^2$
And the initial potential energy is :
$=\ \frac{-GMm}{R}$
Thus total initial energy is given by :
$=\ \frac{1}{2}mv^2\ +\ \frac{-GMm}{R}$
Further, it is given that 20 per cent of kinetic energy is lost.
So the net initial energy is :
$=\ 0.4mv^2\ -\ \frac{GMm}{R}$
The final energy is given by :
$=\ \frac{GMm}{R\ +\ h}$
Using the law of energy conservation, we get :
$0.4mv^2\ -\ \frac{GMm}{R}\ =\ \frac{GMm}{R\ +\ h}$
Solving the above equation, we get :
$h\ =\ \frac{R}{\frac{GM}{0.4v^2R}\ -\ 1}$
or $h=\ \frac{0.4R^2v^2}{GM\ -\ 0.4v^2R}$
or $h=\ \frac{18.442\times 10^{18}}{42.688\times 10^{12}\ -\ 5.432\times 10^{12}}$
or $h=\ 495\times 10^3\ m$
or $h=\ 495\ Km$
Thus, the required distance is 495 Km.
Class 11 Physics Chapter 7 - Gravitation: Higher Order Thinking Skills (HOTS) Questions
Class 11 Physics Chapter 7 - Gravitation Higher Order Thinking Skills (HOTS) questions challenge the students to use concepts in unfamiliar and complex situations. These questions are not mere direct formulas and challenge more in-depth reasoning, understanding and analytical capability. They are particularly good at enhancing competitive exam skills, such as JEE
Question 1: Earth has a mass of 8 inches and a radius of 2 times that of a planet. If the escape velocity from the earth is $11.2 \mathrm{~km} / \mathrm{s}$, the escape velocity in $\mathrm{km} / \mathrm{s}$ from the planet will be:
1) 11.2
2) 5.6
3) 2.8
4) 8.4
Solution:
$
\begin{aligned}
& \mathrm{v}_{\text {escape }}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}} \\
& \frac{\left(\mathrm{~v}_{\text {escape }}\right)_{\text {Planet }}}{\left(\mathrm{v}_{\text {escape }}\right)_{\text {Earth }}}=\sqrt{\left(\frac{\mathrm{M}_{\mathrm{P}}}{\mathrm{M}_{\mathrm{E}}}\right) \times\left(\frac{\mathrm{R}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{P}}}\right)}=\frac{1}{2} \\
& \left(\mathrm{~v}_{\text {escape }}\right)_{\text {Planet }}=\frac{1}{2}\left(\mathrm{~v}_{\text {escape }}\right)_{\text {Earth }}=5.6 \mathrm{~km} / \mathrm{s}
\end{aligned}
$
Hence, the answer is option (2).
Question 2: A satellite of mass $\frac{M}{2}$ is revolving around Earth in a circular orbit at a height of $\frac{R}{3}$ from the Earth's surface. The angular momentum of the satellite is $M \sqrt{\frac{\text { GMR }}{x}}$. The value of $x$ is _____ where $M$ and $R$ are the mass and dive of earth, respectively. ( $G$ is the gravitational constant.)
Solution:
If Earth is assumed to be stationary
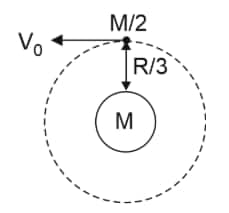
orbital velocity $\mathrm{v}_0=\sqrt{\frac{\mathrm{GM}}{4 \mathrm{R} / 3}}=\sqrt{\frac{3 \mathrm{GM}}{4 \mathrm{R}}}$
Angular momentum of satellite $=\frac{M}{2} v_0 \frac{4 R}{3}$
$\begin{aligned} & =\frac{M}{2} \cdot \sqrt{\frac{3 \mathrm{GM}}{4 \mathrm{R}}} \cdot \frac{4 \mathrm{R}}{3} \\ & =M \sqrt{\frac{\mathrm{GMR}}{3}} \\ & x=3\end{aligned}$
Question 3: A satellite is launched into a circular orbit of radius ' $R$ ' around the Earth. A second satellite is launched into an orbit of radius $1.03 R$. The time period of revolution of the second satellite is approximately larger than the first one by:-
1) $3 \%$
2) $ 4.5 \% $
3) $ 9 \% $
4) $ 2.5 \% $
Solution:
$
\begin{aligned}
&\begin{aligned}
& \mathrm{T}^2=\mathrm{KR}^3 \\
& \frac{2 \Delta \mathrm{~T}}{\mathrm{~T}}=\frac{3 \Delta \mathrm{R}}{\mathrm{R}} \\
& \frac{2 \Delta \mathrm{~T}}{\mathrm{~T}}=\frac{3 \times 0.03 \mathrm{R}}{\mathrm{R}} \\
& \frac{\Delta \mathrm{~T}}{\mathrm{~T}}=\frac{3 \times 0.03}{2} \times 100=4.5 \%
\end{aligned}\\
&\text { Hence, the answer is option (2). }
\end{aligned}
$
Question 4: If a satellite orbiting the Earth is 9 times closer to the Earth than the Moon, what is the time period of rotation of the satellite? Given the rotational time period of the Moon $=27$ days, and the gravitational attraction between the satellite and the moon is neglected.
1) 1 day
2) 81 days
3) 27 days
4) 3 days
Solution:
$
\begin{aligned}
&\begin{aligned}
& \mathrm{T}^2 \propto \mathrm{R}^3 \\
& \left(\frac{\mathrm{~T}_{\mathrm{m}}}{\mathrm{~T}_{\mathrm{s}}}\right)^2=\left(\frac{\mathrm{R}}{\mathrm{R} / 9}\right)^3 \\
& \frac{\mathrm{~T}_{\mathrm{m}}}{\mathrm{~T}_{\mathrm{s}}}=(3)^3 \\
& \Rightarrow \mathrm{~T}_{\mathrm{s}}=\left(\frac{27}{27}\right)=1 \text { day }
\end{aligned}\\
&\text { Hence, the answer is option (1). }
\end{aligned}
$
Question 5: An object of mass $m$ is projected from the origin in a vertical xy plane at an angle $45^{\circ}$ with the $x$-axis with an initial velocity $v_0$. The magnitude and direction of the angular momentum of the object with respect to the origin, when it reaches the maximum height, will be [g is the acceleration due to gravity]
1) $\frac{\mathrm{mv}_0^3}{2 \sqrt{2} \mathrm{~g}}$ along negative z -axis
2) $\frac{m v_0^3}{2 \sqrt{2} g}$ along negative $z$-axis
3) $\frac{m v_0^3}{2 \sqrt{2} g}$ along positive $z$-axis
4) $\frac{m v_0^3}{4 \sqrt{2} g}$ along negative $z$-axis
Solution:
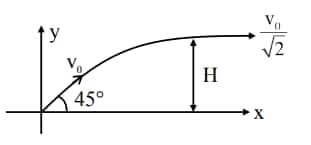
$\mathrm{H}=\frac{\left(\frac{\mathrm{v}_0}{\sqrt{2}}\right)^2}{2 \mathrm{~g}}=\frac{\mathrm{v}_0^2}{4 \mathrm{~g}} \\$
$ \mathrm{~L}=\mathrm{mvh} \\$
$ \mathrm{~L}=\mathrm{m} \frac{\mathrm{v}_0}{\sqrt{2}} \frac{\mathrm{v}_0^2}{4 \mathrm{~g}}$
Hence, the answer is option (4).
Class 11 Physics Chapter 7 - Gravitation: Topics
Class 11 Physics Chapter 7 - Gravitation, covers the first basic force, which is known to hold the motion of a planet as well as celestial mechanics. It makes children realise why objects tend to attract one another by virtue of their mass and the universal force that influences both earthly and space events. This chapter provides the foundation for more in-depth physics and astronomy.
7.1 Introduction
7.2 Kepler’s Laws
7.3 Universal Law Of Gravitation
7.4 The Gravitational Constant
7.5 Acceleration Due To Gravity Of The Earth
7.6 Acceleration Due To Gravity Below And Above The Surface Of Earth
7.7 Gravitational Potential Energy
7.8 Escape Speed
7.9 Earth Satellites
7.10 Energy Of An Orbiting Satellite
Class 11 Physics Chapter 7 - Gravitation question answers: Important Formulae
Gravitation NCERT Solutions: Important Formulae provides important formulas of Gravitation, which include Newton's law of gravitation, gravitational acceleration, velocity in orbital motion, velocity required to escape Earth, and the motion of satellites. These are important formulas that would help in solving numerical problems faster and enhance conceptual knowledge for both board and competitive exams.
1. Gravitational Force
$ F=\frac{G m_1 m_2}{r^2} $
2. Acceleration Due to Gravity (g)
$ g=\frac{G M}{R^2} $
3. Gravitational Potential
$ V=-\int \vec{I} \cdot \overrightarrow{d r} \text { or } V=-\frac{W}{m}=-\int \frac{\vec{F} \cdot \overrightarrow{d r}}{m} $
4. Work Done Against Gravity
$ W=\Delta U=G M m\left[\frac{1}{r_1}-\frac{1}{r_2}\right] $
5. Escape Velocity
$ V_c=\sqrt{\frac{2 G M}{R}} $
6. Kepler's Laws
$ \begin{aligned} & \frac{d A}{d t}=\frac{L}{2 m} \\ & T^2 \alpha a^3 \end{aligned} $
7. Orbital speed
$
v=\sqrt{\frac{G M}{r}}
$
8. Time period of revolution:
$
T=2 \pi \sqrt{\frac{r^3}{G M}}
$
9. Energy of Satellite-
$ E=-\frac{G M m}{2 r} $
How Can NCERT Solutions for Class 11 Physics Chapter 7 Help in Exam Preparation?
Class 11 physics chapter 7 Gravitation question answers help students to gain a clearer insight into the action of gravity, not only on the Earth but also in space. Through these Class 11 Physics Gravitation question answers, one can easily understand how the planets move, objects fall and why artificial satellites remain in space. The step-by-step explanations and solved numericals help students practice derivations like acceleration due to gravity and gravitational potential energy with confidence. These Gravitation NCERT Solutions can also enable the students to take both board and competitive exams by enhancing their familiarity with formulas and increasing their capacity to solve real-life problems connected with gravitation.
Approach to Solve Questions of Class 11 Physics Chapter 7 - Gravitation
Problems in gravitation would need a step-by-step approach and not memorising formulas. It is just a matter of critically examining what has been provided in the question, determining the physical quantities in the question, and then using the correct laws or equations in a logical manner. Even difficult numerical and conceptual questions will be easier to manage with a clear and organised method of approach.
How to Apply Conservation Laws
- When dealing with complex problems, it becomes useful to apply principles of energy conservation and momentum conservation:
- Energy remains preserved if all processes lack non-conservative forces.
- The method aids in solving problems linked to orbital alterations, along with escape motions and falling situations.
Effective Problem-Solving Tips
- Use clear diagrams to represent forces along with their distances.
- Competitive exams require using SI units, and therefore, you must verify unit consistency.
Identify Whether the Problem Involves:
- Point masses
- Spherically symmetric objects
- Satellite or orbital dynamics
- When dealing with several forces or fields, it is necessary to perform vector addition.
Importance of NCERT Solutions for Class 11 Physics Chapter 7: Gravitation
Gravitation NCERT Solutions are also important in learning how gravitational forces control the movement of both heavenly and earthly bodies. This chapter relates the daily experiences and the universal physical laws, and it is a major constituent of mechanics.
- Helps students are able to understand the law of universal gravitation and its practical uses.
- Describes concepts that are of significance, like gravitational field, gravitational potential, and potential energy, in an organised manner.
- Establishes the base of higher concepts such as satellites, orbital movements and astrophysics.
- Plays an important role in CBSE board exams, where numerical and conceptual questions from gravitation are frequently asked.
- Class 11 Physics chapter 7 Gravitation solutions are very helpful in the competitive exams such as JEE and NEET, mostly questions on satellites and gravitational motion.
- Gravitation class 11 question answers enhance problem-solving abilities with step-by-step numerical solution of problems that involve force, acceleration due to gravity and orbits.
- Helps students to connect the theory with phenomena in real life, like free fall, planet movement and tides.
- NCERT Solutions for Class 11 Physics Chapter 7 Gravitation enables accurate application of formulas in different physical situations involving gravity.
What Students Learn from NCERT Solutions for Class 11 Physics Chapter 7: Gravitation?
In Gravitation, the chapter, students are introduced to one of the most important forces of nature, which affects falling objects from the speed of planets. By using Class 11 Physics chapter 7 Gravitation question answers, students acquire a good knowledge of how the law of gravitation works at various levels and how they apply it in the resolution of numerical and conceptual problems.
- Study the law of universal gravitation by Newton and its use in accounting for the attraction between any two masses.
- Know acceleration due to gravity (g) and its dependence on height, depth and latitude.
- Learn the concepts of gravitational field, gravitational potential and gravitational potential energy.
- Get to know how to solve problems that are under the influence of free fall and motion that are under the influence of gravity.
- Know the satellite motion, orbital velocity, time period and energy of a satellite.
- One of the applications of gravitation can be found in the movement of planets and the study of celestial mechanics.
- Develop strong numerical problem-solving skills through step-by-step solutions.
- Develop theoretical understanding as needed in CBSE board examination and competitive examinations such as JEE and NEET.
What Extra Should Students Study Beyond the NCERT for JEE/NEET?
Competitive examinations such as JEE or NEET require students to move past the NCERT textbook in Chapter 7 Gravitation and brush up on their conceptual understanding and solving speed. This involves studying higher-grade types of numerical problems, the nature of real-life applications, more detailed theory behind gravitational potential energy, the motion of satellites, and escape velocity.
NCERT Solutions for Class 11 Physics Chapter-Wise
NCERT Solutions of Class 11 Physics are systematically arranged to equip the learner with a thorough understanding of concepts and improve problem-solving skills. These solutions are in line with the new CBSE syllabus and solutions are both theoretical and numerical and are done in steps. By using chapter-wise links, students will find it easier to study one topic at a time and revise methodically.
NCERT Solutions for Class 11 Subject-wise
Also, check the NCERT Books and the NCERT Syllabus here
- NCERT Books Class 11 Physics
- NCERT Syllabus Class 11 Physics
- NCERT Books Class 11
- NCERT Syllabus Class 11
Subject-Wise NCERT Exemplar Solutions
Frequently Asked Questions (FAQs)
The concept of gravitation is the basis of studying planetary motion, orbits, satellites and gravitation is also important in competitive exams since there is a conceptual and numerical weight to
Yes, the solutions include not only conceptual questions but also numerical ones, step-by-step explanations are also included.
Yes, it contains higher order thinking skills (HOTS) based questions and answers of challenging practice.
Yes, revised NCERT solutions are according to 2025-26 CBSE curriculum and modification done by NCERT.
Yes, when there is no air resistance all objects will fall at the same rate irrespective of mass since they are naturally pulled by gravity that has uniform acceleration.
Yes, gravitation numericals in Class 11 Physics are important as they deepen conceptual understanding and are often featured in exams like board exams and competitive tests.
NCERT Solutions for Class 11 Physics Chapter 8 are important for exams because they help students clearly understand concepts like stress, strain, elasticity, and Hooke’s law. These solutions simplify complex derivations, provide step-by-step explanations, and include important formulas that are frequently asked in board and competitive exams like JEE and NEET.
They describe the daily and celestial theories like free fall, planetary and tidal movements and satellites orbits with simple logic and step-by-step understanding of mathematics.
All key derivations are provided step by step, such as the derivation of the gravitational force, acceleration due to gravity, and orbital velocity.
Yes, the solutions highlight correct sign conventions, units, and conditions of applicability, helping students avoid common errors.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
