Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 7.4 Class 10 Maths Chapter 7 - Coordinate Geometry

NCERT Solutions for Exercise 7.4 Class 10 Maths Chapter 7 - Coordinate Geometry

Edited By Safeer PP | Updated on Jul 07, 2022 05:02 PM IST | #CBSE Class 10th

NCERT Solutions for Class 10 Maths exercise 7.4 is the final and optional exercise in this chapter, and it covers all of the concepts from the entire chapter, including the distance formula, section formula, and triangle area. Coordinate Geometry is the study of geometry using coordinate points. The distance formula used to find the distance between two points in a two-dimensional plane is known as the Euclidean distance formula. The section formula is used to get the coordinates of the point that splits a line segment into a ratio either externally or internally. We can utilize the section when a point divides a line segment in some ratio either externally or internally.

This Story also Contains
  1. Coordinate Geometry Class 10 Chapter 7 Exercise: 7.1
  2. More About NCERT Solutions for Class 10 Maths Exercise 7.4:
  3. Benefits of NCERT Solutions for Class 10 Maths Exercise 7.4 :

NCERT solutions for Class 10 Maths chapter 7 exercise 7.4 consists of 8 questions in which 6 of them are long answer questions, 1 is a practical based question and the remaining 1 is a reasoning question. In NCERT book Class 10 Maths chapter 7 exercise 7.4, the ideas linked to the solution of coordinate geometry are well discussed. The following activities are included along with NCERT syllabus Class 10 Maths chapter 7 exercise 7.4.

Coordinate Geometry Class 10 Chapter 7 Exercise: 7.1

Q1 Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).

Answer:

Let the line divide the line segment AB in the ratio k:1 at point C.

Then, the coordinates of point C will be:

C(x,y) = \left ( \frac{3k+2}{k+1},\frac{7k-2}{k+1} \right )

Point C will also satisfy the given line equation 2x + y - 4 = 0 , hence we have

\Rightarrow 2\left ( \frac{3k+2}{k+1} \right )+\left (\frac{7k-2}{k+1} \right ) - 4 = 0

\Rightarrow \frac{6k+4+7k-2-4k-4}{k+1} = 0

\Rightarrow 9k-2 = 0

\Rightarrow k=\frac{2}{9}

Therefore, the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points A(2,-2) and B(3,7) is 2:9 internally.

Q2 Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.

Answer:

If the points (x, y), (1, 2)\ and\ (7, 0) are collinear then, the area formed by these points will be zero.

The area of the triangle is given by,

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ] = 0

Substituting the values in the above equation, we have

Area = \frac{1}{2}\left [ x(2-0)+1(0-y)+7(y-2) \right ]= 0

\Rightarrow 2x-y+7y-14= 0

Or,

\Rightarrow x+3y-7= 0

Hence, the required relation between x and y is x+3y-7= 0 .

Q3 Find the center of a circle passing through the points (6, – 6), (3, – 7) and (3, 3).

Answer:

From the figure:

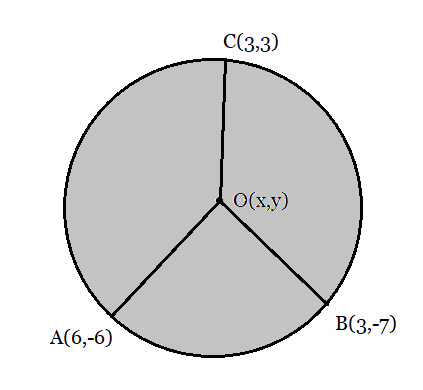
1638427419480

Let the center point be O(x,y) .

Then the radii of the circle OA,\ OB,\ and\ OC are equal.

The distance OA:

OA = \sqrt{(x-6)^2+(y+6)^2}

The distance OB:

OB = \sqrt{(x-3)^2+(y+7)^2}

The distance OC:

OC = \sqrt{(x-3)^2+(y-3)^2}

Equating the radii of the same circle.

When equating, OA = OB

\sqrt{(x-6)^2+(y+6)^2}= \sqrt{(x-3)^2+(y+7)^2}

Squaring both sides and applying a^2-b^2 = (a+b)(a-b)

\Rightarrow (x-6+x-3)(x-6-x+3)+(y+6+y+7)(y+6-y-7) = 0

\Rightarrow (2x-9)(-3) + (2y+13)(-1) = 0

\Rightarrow -6x+27-2y-13 = 0 or

\Rightarrow 3x+y -7= 0 ...................................(1)

When equating, OA = OC

\sqrt{(x-6)^2+(y+6)^2}= \sqrt{(x-3)^2+(y-3)^2}

Squaring both sides and applying a^2-b^2 = (a+b)(a-b)

\Rightarrow (x-6+x-3)(x-6-x+3)+(y+6+y-3)(y+6-y+3) = 0

\Rightarrow (2x-9)(-3) + (2y+3)(9) = 0

\Rightarrow -3x+9y+27 = 0 ...................................(2)

Now, adding the equations (1) and (2), we get

\Rightarrow 10y = -20

\Rightarrow y = -2 .

From equation (1), we get

\Rightarrow 3x-2 = 7

\Rightarrow 3x =9

\Rightarrow x =3

Therefore, the centre of the circle is (3,-2) .

Q4 The two opposite vertices of a square are (–1, 2) and (3, 2). Find the coordinates of the other two vertices.

Answer:

From the figure:

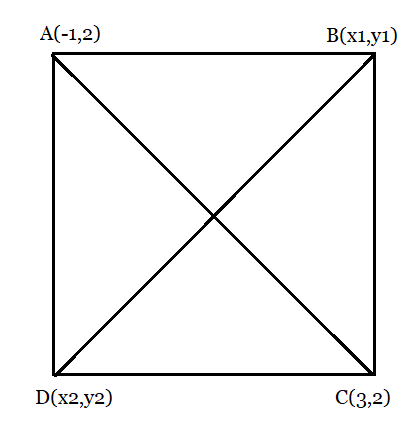
1638427461655

We know that the sides of a square are equal to each other.

Therefore, AB = BC

So,

\sqrt{(x-1)^2+(y-2)^2} = \sqrt{(x-3)^2+(y-2)^2}

Squaring both sides, we obtain

\implies (x-1)^2+(y-2)^2 = (x-3)^2+(y-2)^2

Now, doing \left ( a^2-b^2 = (a+b)(a-b) \right )

We get

\implies (x-1+x-3)(x-1-x+3) = 0

Hence x = 2 .

Applying the Pythagoras theorem to find out the value of y.

AB^2+BC^2 = AC^2

(\sqrt{(2-1)^2+(y-2)^2})^2 + (\sqrt{(2-3)^2+(y-2)^2})^2 = (\sqrt{(3+1)^2+(2-2)^2})^2

\Rightarrow \left (\sqrt{1+(y-2)^2} \right )^2 + \left (\sqrt{1+(y-2)^2} \right )^2 = \left (\sqrt{16} \right )^2

\Rightarrow (y-2)^2 = 7

Q5 (i) The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar is planted on the boundary at a distance of 1m from each other. There is a triangular grassy lawn in the plot as shown in Fig. 7.14. The students are to sow seeds of flowering plants on the remaining area of the plot. (i) Taking A as origin, find the coordinates of the vertices of the triangle.

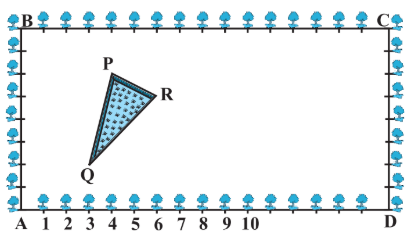
1638427489636

Answer:

Taking A as origin then, the coordinates of P, Q, and R can be found by observation:

Coordinates of point P is (4,6).

Coordinates of point Q is (3,2).

Coordinates of point R is (6,5).

The area of the triangle, in this case, will be:

Area =\frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

=\frac{1}{2}\left [ 4(2-5)+3(5-6)+6(6-2) \right ]

=\frac{1}{2}\left [ -12-3+24\right ] = \frac{9}{2}\ Square\ units.

Q5 (ii) The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar is planted on the boundary at a distance of 1m from each other. There is a triangular grassy lawn in the plot as shown in Fig. 7.14. The students are to sow seeds of flowering plants on the remaining area of the plot. (ii) What will be the coordinates of the vertices of D PQR if C is the origin? Also, calculate the areas of the triangles in these cases. What do you observe?


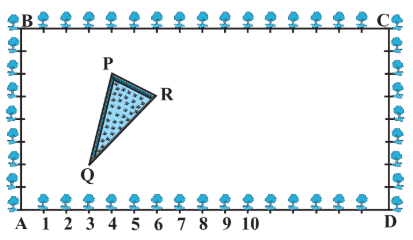
1638427504689

Answer:

Taking C as origin, then CB will be x-axis and CD be y-axis.

The coordinates fo the vertices P, Q, and R are: (12,2),\ (13,6),\ (10,3). respectively.

The area of the triangle, in this case, will be:

Area =\frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

=\frac{1}{2}\left [ 12(6-3)+13(3-2)+10(2-6) \right ]

=\frac{1}{2}\left [ 36-13+40 \right ] = \frac{9}{2}\ Square\ units.

It can be observed that in both cases the area is the same so, it means that the area of any figure does not depend on the reference which you have taken.

Q6 The vertices of a \Delta ABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that \frac{AD }{AB} = \frac{AE }{AC } = \frac{1}{4} Calculate the area of the \Delta ADE and compare it with the area of \Delta ABC .

Answer:

From the figure:

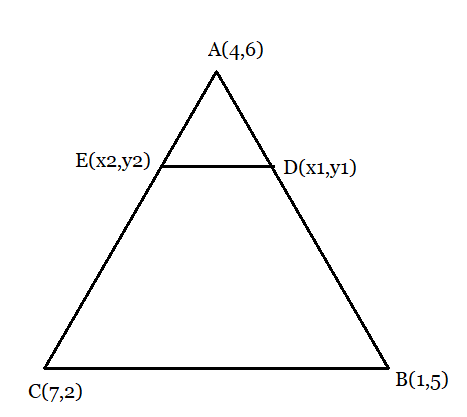
1638427528989

Given ratio:

\frac{AD }{AB} = \frac{AE }{AC } = \frac{1}{4}

Therefore, D and E are two points on side AB and AC respectively, such that they divide side AB an AC in the ratio of 1:3 .

Section formula:

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Then, coordinates of point D:

D(x_{1},y_{1})= \left (\frac{1\times1+3\times 4}{1+3} , \frac{1\times 5+3\times 6}{1+3} \right )

Coordinates of point E:

E(x_{2},y_{2})= \left (\frac{1\times7+3\times 4}{1+3} , \frac{1\times 2+3\times 6}{1+3} \right )

= \left ( \frac{19}{4}, \frac{20}{4} \right )

Then, the area of a triangle:

= \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

Substituting the values in the above equation,

Area\ of\ \triangle ADE = \frac{1}{2}\left [ 4\left ( \frac{23}{4} - \frac{20}{4}\right )+\frac{13}{4}\left ( \frac{20}{4} - 6 \right )+\frac{19}{4}\left (6-\frac{23}{4} \right )\right ] = \frac{1}{2}\left [ 3-\frac{13}{4} +\frac{19}{16}\right ] = \frac{1}{2}\left [ \frac{48-52+19}{16} \right ] = \frac{15}{32}\ square\ units.

Area\ of\ \triangle ABC = \frac{1}{2}\left [ 4(5-2)+1(2-6)+7(6-5) \right ]

= \frac{1}{2}\left [ 12-4+7 \right ] = \frac{15}{2}\ Square\ units.

Hence the ratio between the areas of \triangle ADE and \triangle ABC is 1:16.

Q7 (1) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of \triangle ABC . The median from A meets BC at D. Find the coordinates of the point D.

Answer:

From the figure:

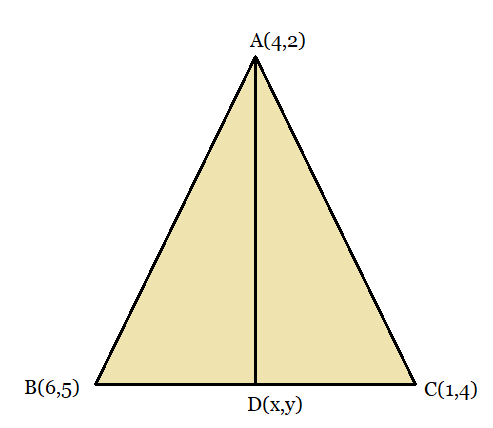
1638427550821

Let AD be the median of the triangle

Then, D is the mid-point of BC

Coordinates of Point D:

\left ( \frac{6+1}{2},\frac{5+4}{2} \right ) = \left ( \frac{7}{2}, \frac{9}{2} \right )

Q7 (ii) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of D ABC. Find the coordinates of the point P on AD such that AP: PD = 2: 1

Answer:

From the figure,

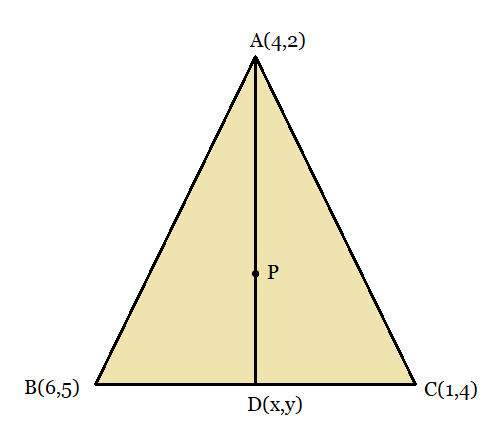
1638427579264

The point P divides the median AD in the ratio, AP: PD = 2: 1

Hence using the section formula,

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

P(x,y)= \left (\frac{2\times\frac{7}{2}+1\times4}{2+1} , \frac{2\times\frac{9}{2}+1\times2}{2+1} \right ) = \left ( \frac{11}{3}, \frac{11}{3} \right )

Q7 (iii) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of D ABC. Find the coordinates of points Q and R on medians BE and CF respectively such that BQ: QE = 2: 1 and CR: RF = 2: 1

Answer:

From the figure,

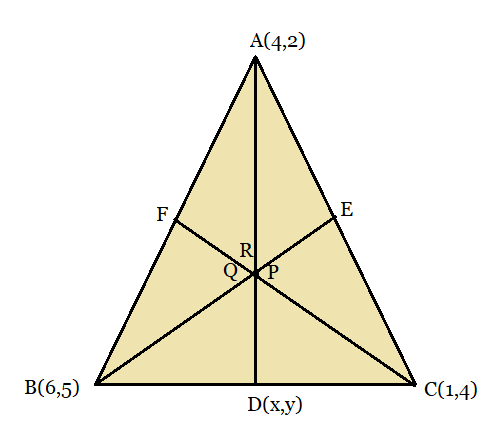
1638427609335

\Rightarrow The point Q divides the median BE in the ratio, BQ : QE = 2 : 1

Hence using the section formula,

Q(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Q(x,y)= \left (\frac{2\times\frac{5}{2}+1\times6}{2+1} , \frac{2\times3+1\times5}{2+1} \right ) = \left ( \frac{11}{3}, \frac{11}{3} \right )

\Rightarrow The point R divides the median CF in the ratio, CR: RF = 2: 1

Hence using the section formula,

R(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

R(x,y)= \left (\frac{2\times 5+1\times1}{2+1} , \frac{2\times\frac{7}{2}+1\times4}{2+1} \right ) = \left ( \frac{11}{3}, \frac{11}{3} \right )

Q7 (iv) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of D ABC. What do you observe?

Answer:

We observed that the coordinates of P, Q, and R are the same. Therefore, all these are representing the same point on the plane. i.e., the centroid of the triangle.

Q7 (v) Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of \triangle ABC . If A(x_1, y_1), B(x_2, y_2)\ and\ C(x_3, y_3) are the vertices of \triangle ABC , find the coordinates of the centroid of the triangle.

Answer:

From the figure, 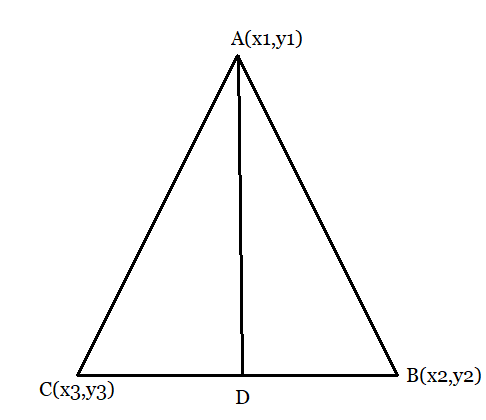1656326442871

Let the median be AD which divides the side BC into two equal parts.

Therefore, D is the mid-point of side BC.

Coordinates of D:

= \left ( \frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2} \right )

Let the centroid of this triangle be O.

Then, point O divides the side AD in a ratio 2:1.

Coordinates of O:

= \left ( \frac{2\times\frac{x_{2}+x_{3}}{2}+1\times x_{1}}{2+1}, \frac{2\times\frac{y_{2}+y_{3}}{2}+1\times y_{1} }{2+1} \right )

= \left ( \frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3} \right )

Q8 ABCD is a rectangle formed by the points A(–1, –1), B(– 1, 4), C(5, 4) and D(5, – 1). P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.

Answer:

From the figure:

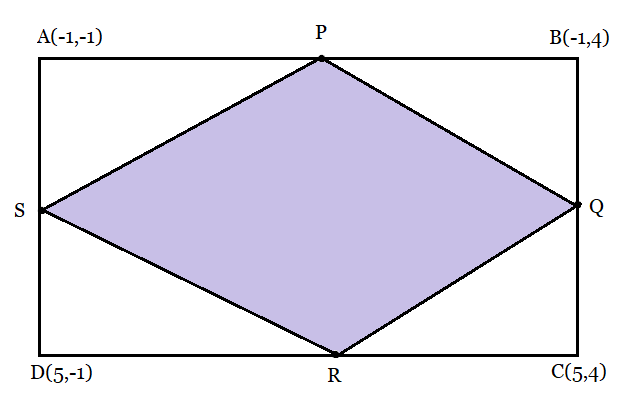
1638427884180

P is the mid-point of side AB.

Therefore, the coordinates of P are, \left ( \frac{-1-1}{2}, \frac{-1+4}{2} \right ) = \left ( -1, \frac{3}{2} \right )

Similarly, the coordinates of Q, R and S are: \left ( 2,4 \right ),\ \left ( 5, \frac{3}{2} \right ),\ and\ \left ( 2,-1 \right ) respectively.

The distance between the points P and Q:

PQ = \sqrt{(-1-2)^2+\left ( \frac{3}{2} -4 \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

and the distance between the points Q and R:

QR = \sqrt{(2-5)^2+\left ( 4-\frac{3}{2} \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

Distance between points R and S:

RS = \sqrt{(5-2)^2+\left ( \frac{3}{2}+1 \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

Distance between points S and P:

SP = \sqrt{(2+1)^2+\left ( -1-\frac{3}{2} \right )^2} = \sqrt{9+\frac{25}{4}} = \sqrt{\frac{61}{4}}

Distance between points P and R the diagonal length:

PR = \sqrt{(-1-5)^2+\left ( \frac{3}{2}-\frac{3}{2} \right )^2} = 6

Distance between points Q and S the diagonal length:

QS = \sqrt{(2-2)^2+\left ( 4+1 \right )^2} = 5

Hence, it can be observed that all sides have equal lengths. However, the diagonals are of different lengths.

Therefore, PQRS is a rhombus.

More About NCERT Solutions for Class 10 Maths Exercise 7.4:

The midpoint and area of the quadrilateral were also covered in the NCERT solutions for Class 10 Maths exercise 7.4. The questions in exercise 7.3 Class 10 Maths are based on concepts such as the distance formula, section formula, and triangle area. When a point P(x,y) divides the line segment into two segments, with marked points as A(x1,y1) and B(x2,y2) the method used to find the coordinates of that point is known as the section formula that is covered in the Class 10 Maths chapter 7 exercise 7.4.

Also Read| Coordinate Geometry Class 10 Notes

Benefits of NCERT Solutions for Class 10 Maths Exercise 7.4 :

• NCERT solutions for Class 10 Maths exercise 7.4 are carefully drafted to assist the student in scoring good marks in the examination. That's why any student can easily score the highest possible marks in the final exam.

• From exercise 7.4 Class 10 Maths we can easily understand the pattern of questions that can be asked in term exams from this chapter and also know the marks weightage of the chapter. From that, they can prepare themselves accordingly for the final examination.

• NCERT solution for Class 10 Maths chapter 7 exercise 7.4 exercises, will be helpful in the further exercise of chapter 10.

Frequently Asked Questions (FAQs)

1. The distance of the point P(4, 9) from the x-axis is _______

The distance from x-axis is equal to its ordinate that is 4 .

2. The distance of the point P(4, 9) from the y-axis is _______

The distance from the x-axis is equal to its ordinate that is 9.

3. State true/false : The area of the triangle is always positive .

The statement is true. The area of the triangle is always positive.

4. Using the area of the triangle formula, how can we find the area of the quadrilateral?

Quadrilaterals can be divided into three triangular areas, each with its own area. The area of the two triangles can then be calculated using the area of the triangle formula. The area of the quadrilateral is then calculated by adding both.

5. Area of the quadrilateral is always _______

The area of the quadrilateral is always positive since the area of the triangle is positive.

6. According to NCERT solutions for Class 10 Maths chapter 7 exercise 7.4 , define collinear points ?

Two or more points are considered to be collinear if they lie on the same line, according to NCERT solutions for Class 10 Maths chapter 7 exercise 7.4.

7. How many questions are there in the NCERT solutions for Class 10 Maths chapter 7 exercise 7.4 and what types of questions are there?

NCERT solutions for Class 10 Maths chapter 7 exercise 7.4  consists of 8 questions in which 6 of them are long answer questions, 1 is a practical based question and remaining 1 is a reasoning question and all the questions are based on topics such as distance formula, section formula, area of the triangle, midpoint and collinearity.

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:01 August,2024 - 16 September,2024

National Rural Talent Scholarship Examination

Application Date:05 September,2024 - 20 September,2024

National Institute of Open Schooling 10th examination

Admit Card Date:13 September,2024 - 07 October,2024

National Institute of Open Schooling 12th Examination

Admit Card Date:13 September,2024 - 07 October,2024

Nagaland Board of Secondary Education 12th Examination

Application Date:17 September,2024 - 30 September,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

Hello

The Sadhu Ashram in Aligarh is located in Chhalesar . The ashram is open every day of the week, except for Thursdays . On Mondays, Wednesdays, and Saturdays, it's open from 8:00 a.m. to 7:30 p.m., while on Tuesdays and Fridays, it's open from 7:30 a.m. to 7:30 p.m. and 7:30 a.m. to 6:00 a.m., respectively . Sundays have varying hours from 7:00 a.m. to 8:30 p.m. . You can find it at Chhalesar, Aligarh - 202127 .

Read Complete Answer
vaibhavi bhalsod 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Pearson | PTE
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer! Trusted by 3,500+ universities globally

View All Application Forms
News and Notifications
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST
CBSE conducts surprise inspections at 27 schools in Rajasthan, Delhi to curb menace of dummy schools
September 03, 2024 - 03:02 PM IST
CBSE Class 10 compartment result 2024 declared; 48.83% pass
August 05, 2024 - 03:14 PM IST
CBSE Class 10 compartment result 2024 soon; passing marks, websites to check
August 05, 2024 - 02:44 PM IST
CBSE Class 10 compartment result 2024 expected soon at cbseresults.nic.in; grading system, passing marks
August 04, 2024 - 04:20 PM IST
CBSE Class 10 compartment result 2024 soon at cbseresults.nic.in; websites to check
August 03, 2024 - 04:38 PM IST
CBSE 10th, 12th revaluation lot 2 result 2024 out at cbseresults.nic.in; passing marks
July 30, 2024 - 06:39 PM IST

Stay up-to date with CBSE Class 10th News

Back to top