Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 7.3 Class 10 Maths Chapter 7 - Coordinate Geometry

NCERT Solutions for Exercise 7.3 Class 10 Maths Chapter 7 - Coordinate Geometry

Edited By Safeer PP | Updated on Jul 07, 2022 04:58 PM IST | #CBSE Class 10th

NCERT Solutions for Class 10 Maths exercise 7.3 deals with the concept of the area of the triangle. A triangle is nothing but a polygon with three edges and three vertices. In a two-dimensional plane, the area of a triangle is the space that it covers, and its area is equal to half the product of its base and height. Coordinate geometry is the study of geometry using coordinate points. In coordinate geometry, the area of the triangle can be calculated by the three vertices of the triangle which are given in the coordinate plane. In exercise 7.3 Class 10 Maths.

This Story also Contains
  1. Coordinate Geometry Class 10 Chapter 7 Exercise: 7.1
  2. More About NCERT Solutions for Class 10 Maths Exercise 7.3
  3. Benefits of NCERT Solutions for Class 10 Maths Exercise 7.3
  4. NCERT Solutions Subject Wise
  5. Subject Wise NCERT Exemplar Solutions

Actually, the area of the triangle formula is calculated using heron's formula. We can also calculate the area of a triangle using the determinant method. Also as the area of the triangle can never be negative, we must take the absolute value. NCERT solutions for Class 10 Maths chapter 7 exercise 7.3 consists of 5 questions in which three are easy and two are moderate and all the questions are based on calculating the area of a triangle. The concepts associated with the answer of coordinate geometry are well explained in NCERT book Class 10 Maths chapter 7 exercise 7.3. Alongside NCERT syllabus Class 10 Maths chapter 7 exercise 7.3 the subsequent exercises also are present.

Coordinate Geometry Class 10 Chapter 7 Exercise: 7.1

Q 1 (i) Find the area of the triangle whose vertices are : (2, 3), (–1, 0), (2, – 4)

Answer:

As we know, the area of a triangle with vertices (x1,x2) ,(y1, y2) and (z1 z2 ) is given by :

A= \frac{1}{2}(x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2))

So Area of a triangle whose vertices are(2, 3), (–1, 0)and (2, – 4) is

A= \frac{1}{2}[2(0-(-4))+(-1)(-4-3)+2(3-0)]

A= \frac{1}{2}[8+7+6]

A= \frac{1}{2}[21]

A= \frac{21}{2}

A= 10.5\:unit^2

Hence, the area of the triangle is 10.5 per unit square.

Q1 (ii) Find the area of the triangle whose vertices are (–5, –1), (3, –5), (5, 2)

Answer:

From the figure:

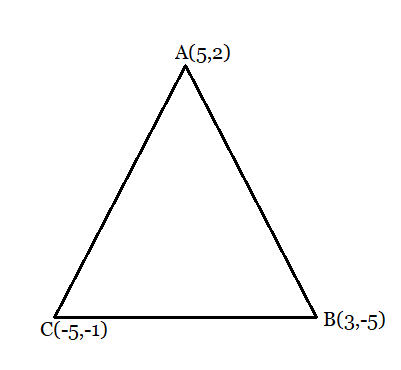
1638427297678

Area of the triangle is given by:

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

Substituting the values in the above equation, we obtain

Area = \frac{1}{2}\left [ (-5)((-5)-(-2))+3(2-(1))+5(-1-(-5)) \right ]

= \frac{1}{2}\left [ 35+9+20 \right ] = 32 \ square\ units.

Q2 (i) In each of the following find the value of ‘k’, for which the points are collinear. (7, –2), (5, 1), (3, k)

Answer:

The points (7, –2), (5, 1), (3, k) are collinear if the area of the triangle formed by the points will be zero.

Area of the triangle is given by:

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ] = 0

Substituting the values in the above equation, we obtain

\frac{1}{2}\left [ 7(1-k)+5(k-(-2))+3(-2-1) \right ] = 0

\left [ 7-7k+5k+10-9 \right ] = 0

\Rightarrow -2k+8 = 0

\Rightarrow k = 4

Hence, the points are collinear for k=4 .

Q2 (ii) In each of the following find the value of ‘k’, for which the points are collinear. (8, 1), (k, – 4), (2, –5)

Answer:

The points (8,1), (k, -4), (2,-5) are collinear if the area of the triangle formed by these points will be zero.

Area of the triangle is given by:

Area = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ] = 0

Substituting the values in the above equation, we obtain

\frac{1}{2}\left [ 8(-4-(-5))+k((-5)-1)+2(1-(-4)) \right ] = 0

\Rightarrow 8-6k+10 = 0

\Rightarrow 6k = 18

\Rightarrow k = 3

Hence, the points are collinear for k = 3 .

Q3 Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Answer:

From the figure:

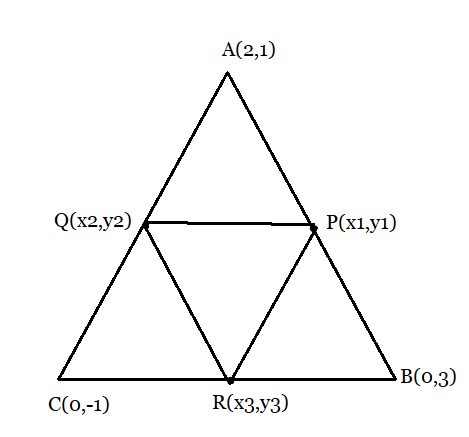
1638427329430

The coordinates of the point P, Q, and R are:

Point P is the midpoint of side AB, hence the coordinates of P are :

P(x_{1},y_{1}) = \left (\frac{0+2}{2}, \frac{3+1}{2} \right ) = \left (1, 2 \right )

Point Q is the midpoint of side AC, hence the coordinates of Q are :

Q(x_{2},y_{2}) = \left (\frac{2+0}{2}, \frac{1-1}{2} \right ) = \left (1, 0 \right )

Point R is the midpoint of side BC, hence the coordinates of R are :

R(x_{3},y_{3}) = \left (\frac{0+0}{2}, \frac{-1+3}{2} \right ) = \left (0, 1 \right )

Hence, the area of the triangle formed by the midpoints PQR will be,

Area_{(PQR)} = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}) \right ]

= \frac{1}{2}\left [ (2-1)+1(1-0)+0(0-2) \right ]

=\frac{1}{2}(1+1) = 1\ square\ units.

And the area formed by the triangle ABC will be:

Area_{(ABC)} = \frac{1}{2}\left [ 0(1-3)+2(3-(-1))+0(-1-1) \right ]

= \frac{1}{2}\left [ 8 \right ] = 4\ square\ units.

Thus, the ratio of Area of \triangle PQR to the Area of \triangle ABC will be 1:4 .

Q4 Find the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5), (3, – 2) and (2, 3).

Answer:

From the figure:

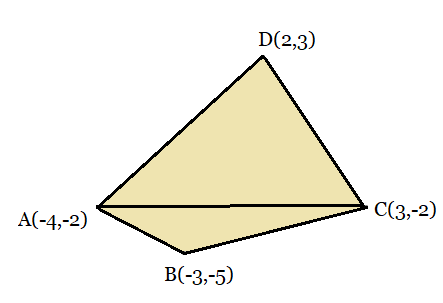
1638427363305

The coordinates are A(-4,-2),\ B(-3,-5),\ C(3,-2)\ and\ D(2,3)

Divide the quadrilateral into 2 parts of triangles.

Then the area will be, ABC + ADC

Area of the triangle formed by ABC will be,

Area_{(ABC)} = \frac{1}{2}\left [ (-4)((-5)-(-2))+(-3)((-2)-(-2))+3((-2)-(-2)) \right ] = \frac{1}{2}\left [ 12+0+9 \right ] = \frac{21}{2}\ Square\ units.

Area of the triangle formed by ADC will be,

Area_{(ADC)} = \frac{1}{2}\left [ (-4)((-2)-(-3))+3(3-(-2))+2((-2)-(-2)) \right ] = \frac{1}{2}\left [ 20+15+0 \right ] = \frac{35}{2}\ Square\ units.

Therefore, the area of the quadrilateral will be:

= \frac{21}{2}+\frac{35}{2} = 28\ square\ units.

Alternatively,

The points A and C are in the same ordinates.

Hence, the length of base AC will be (3-(-4)) = 7\ units.

Therefore,

Area of triangle ABC:

= \frac{1}{2} \times (Base) \times (Height) = \frac{1}{2}\times(7)(3)

Area of triangle ADC:

= \frac{1}{2} \times (Base) \times (Height) = \frac{1}{2}\times(7)(5)

Therefore, the area will be, \frac{1}{2}\times(7)\times(5+3) =28\ square\ units.

Q5 You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for D ABC whose vertices are A(4, – 6), B(3, –2) and C(5, 2).

Answer:

From the figure:

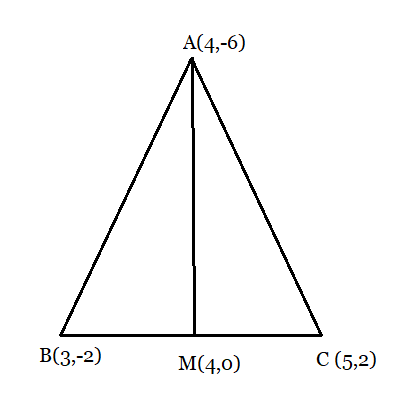
1638427386798

The coordinates of midpoint M of side BC is:

M = \left ( \frac{3+5}{2}, \frac{-2+2}{2} \right ) = \left ( 4,0 \right )

Now, calculating the areas of the triangle ABM and ACM :

Area of triangle, ABM:

Area_{(ABM)} = \frac{1}{2}\left [ 4((-2)-0)+3(0-(-6))+4((-6)-(-2)) \right ]

= \frac{1}{2}\left [ -8+18-16 \right ] = 3\ Square\ units.

Area of triangle, ACM:

Area_{(ACM)} = \frac{1}{2}\left [ 4(0-(-2))+4(2-(-6))+5((-6)-0) \right ]

= \frac{1}{2}\left [ -8+32-30 \right ] = -3\ Square\ units.

However, the area cannot be negative, Therefore, area of \triangle ACM is 3 square units.

Clearly, the median AM divided the \triangle ABC in two equal areas.

More About NCERT Solutions for Class 10 Maths Exercise 7.3

The NCERT Solutions for Class 10 Maths exercise 7.3 also focused on the collinearity and area of the quadrilateral. Exercise 7.3 Class 10 Maths consists of a question based on calculating the area of a triangle and collinearity of three points. Geometrically, two or more points are said to be collinear, if they lie on the same line. Three points are said to be collinear if the area of the triangle is zero. We can also find the area of the quadrilateral by using the area of the triangle formula. Quadrilaterals can be divided into triangular regions which have no common area. Then by using the area of the triangle formula, we can find the area of the two triangles. Then by adding both, we get the area of the quadrilateral. Also, the area of the quadrilateral is never negative as the area of the quadrilateral is positive. Usage of midpoint formula also covered in exercise 7.3 Class 10 Maths.

Also Read| Coordinate Geometry Class 10 Notes

Benefits of NCERT Solutions for Class 10 Maths Exercise 7.3

• NCERT solutions for Class 10 Maths exercise 7.3 is one of the most scoring exercises, as the questions are simple to solve using the given formula.

• Exercise 7.3 Class 10 Maths will encourage us to use real-life references to understand concepts of the area of triangle and collinearity of points.

• By fathoming the NCERT solution for Class 10 Maths chapter 7 exercise 7.3 , understudies can achieve a great score in term exams as well as in competitive examinations like the Joint Entrance Exam Main (JEE Main).

Also, see-

Tallentex 2025 - ALLEN's Talent Encouragement Exam

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

Apply

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. A Triangle is a polygon with _____ edges and vertices.

A Triangle is a polygon with three edges and vertices.

2. State true/false : The area of the triangle is always negative.

The statement is false because the area of the triangle is never negative.

3. What is coordinate geometry?

The study of geometry using coordinate points is known as coordinate geometry.

4. Three points are said to be col linear if the area of the triangle is

Three points are said to be collinear if the area of the triangle is zero.

5. What are non linear points?

Non-linear points are the points that are not possible to draw a straight line through three or more points. 

6. What are the col linear points according to NCERT solutions for Class 10 Maths chapter 7 exercise 7.3 ?

Two or more points are considered to be collinear if they lie on the same line, according to NCERT solutions for Class 10 Maths chapter 7 exercise 7.3.

7. How many questions and what variety of questions are there within the NCERT solutions for Class 10 Maths chapter 7 exercise 7.3 ?

In NCERT solutions for Class 10 Maths chapter 7 exercise 7.3  , are 5 problems, all of which are centred on calculating the area of a triangle.

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:01 August,2024 - 16 September,2024

International General Knowledge Olympiad

Exam Date:19 September,2024 - 19 September,2024

Unified Cyber Olympiad

Exam Date:20 September,2024 - 20 September,2024

International English Olympiad

Exam Date:26 September,2024 - 26 September,2024

International Olympiad of Mathematics

Application Date:30 September,2024 - 30 September,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
can we apply for diploma if we have passed 10th cbse lo

Yes, you can definitely apply for diploma courses after passing 10th CBSE. In fact, there are many diploma programs designed specifically for students who have completed their 10th grade.

Generally, passing 10th CBSE with a minimum percentage (often 50%) is the basic eligibility for diploma courses. Some institutes might have specific subject requirements depending on the diploma specialization.

There is a wide range of diploma courses available in various fields like engineering (e.g., mechanical, civil, computer science), computer applications, animation, fashion design, hospitality management, and many more.

You can pursue diplomas at various institutions like:


Read Complete Answer
Nitin Kumar 14 June,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

PTE Registrations 2024
PTE Registrations 2024
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer!

JEE Main high scoring chapters and topics
JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE Class 10 compartment result 2024 declared; 48.83% pass
August 05, 2024 - 03:14 PM IST
CBSE Class 10 compartment result 2024 soon; passing marks, websites to check
August 05, 2024 - 02:44 PM IST
CBSE Class 10 compartment result 2024 expected soon at cbseresults.nic.in; grading system, passing marks
August 04, 2024 - 04:20 PM IST
CBSE Class 10 compartment result 2024 soon at cbseresults.nic.in; websites to check
August 03, 2024 - 04:38 PM IST
CBSE 10th, 12th revaluation lot 2 result 2024 out at cbseresults.nic.in; passing marks
July 30, 2024 - 06:39 PM IST
CBSE: No open book exams for Classes 10, 12 this year; pilot only in a few schools
June 12, 2024 - 10:52 AM IST
CBSE Class 10 result 2024 revaluation application begins at cbse.gov.in; apply by May 24
May 21, 2024 - 02:20 PM IST

Stay up-to date with CBSE Class 10th News

Back to top