• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 14.3 Class 10 Maths Chapter 14 - Statistics

NCERT Solutions for Exercise 14.3 Class 10 Maths Chapter 14 - Statistics

Edited By Ramraj Saini | Updated on Dec 02, 2023 10:37 AM IST | #CBSE Class 10th
Upcoming Event
CBSE Class 10th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 14 Exercise 14.3

NCERT Solutions for Exercise 14.3 Class 10 Maths Chapter 14 Statistics are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 14.3 introduces us to the concept of finding the median. In ninth grade, we learned about the median of grouped data. The median is a measure of central tendency that represents the value of the data's middle observation. The median depends on the number of observations. The value of the median is different if the number of observations is odd and different if the number of observations is even. This exercise class 10 ex 14.3 feature a variety of questions that cover the complete topic of determining the median in grouped data.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 14 Exercise 14.3
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 14 exercise 14.3
  3. Assess NCERT Solutions for Class 10 Maths chapter 14 exercise 14.3
  4. Statistics C lass 10 Chapter 14 Statistics Exercise: 14.3
  5. More About NCERT Solutions for Class 10 Maths Exercise 14.3
  6. Benefits of NCERT Solutions for Class 10 Maths Exercise 14.3
  7. Key Features For Class 10 Maths Chapter 14 Exercise 14.3
  8. NCERT Solutions for Class 10 Subject Wise
NCERT Solutions for Exercise 14.3 Class 10 Maths Chapter 14 - Statistics
NCERT Solutions for Exercise 14.3 Class 10 Maths Chapter 14 - Statistics

Exercise 14.3 Class 10 Maths also gives us information about what is cumulative frequency column, median class and also we will know about the relation between mean, median and mode. 10th class Maths exercise 14.3 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 14 exercise 14.3

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 14 exercise 14.3

Statistics C lass 10 Chapter 14 Statistics Exercise: 14.3

Q1 The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

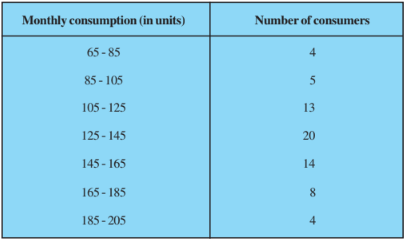
1640762287658

Answer:

Let the assumed mean be a = 130 and h = 20

Class

Number of

consumers f_i

Cumulative

Frequency

Classmark

x_i

d_i = x_i -a

u_i = \frac{d_i}{h}

f_iu_i

65-85

4

4

70

-60

-3

-12

85-105

5

9

90

-40

-2

-10

105-125

13

22

110

-20

-1

-13

125-145

20

42

130

0

0

0

145-165

14

56

150

20

1

14

165-185

8

64

170

40

2

16

185-205

4

68

190

60

3

12



\sum f_i = N

= 68




\sum f_ix_i

= 7

MEDIAN:
N= 68 \implies \frac{N}{2} = 34
\therefore Median class = 125-145; Cumulative Frequency = 42; Lower limit, l = 125;

c.f. = 22; f = 20; h = 20
Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W
\\ = 125 + \left (\frac{34-22}{20} \right ).20 \\ \\ = 125 + 12

= 137

Thus, the median of the data is 137

MODE:

The class having maximum frequency is the modal class.
The maximum frequency is 20 and hence the modal class = 125-145
Lower limit (l) of modal class = 125, class size (h) = 20
Frequency ( f_1 ) of the modal class = 20; frequency ( f_0 ) of class preceding the modal class = 13, frequency ( f_2 ) of class succeeding the modal class = 14.

Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h

\\ = 125 + \left(\frac{20-13}{2(20)-13-14} \right).20 \\ \\ = 125 + \frac{7}{13}.20

= 135.76

Thus, Mode of the data is 135.76

MEAN:

Mean,
\overline x =a + \frac{\sum f_iu_i}{\sum f_i}\times h
= 130 + \frac{7}{68}\times20 = 137.05

Thus, the Mean of the data is 137.05

Q2 If the median of the distribution given below is 28.5, find the values of x and y.

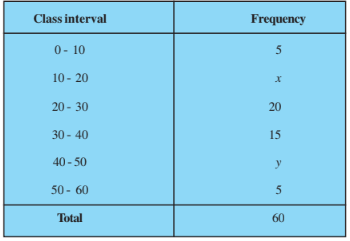
1640762346146

Answer:

Class

Number of

consumers f_i

Cumulative

Frequency

0-10

5

5

10-20

x

5+x

20-30

20

25+x

30-40

15

40+x

40-50

y

40+x+y

50-60

5

45+x+y


\sum f_i = N

= 60



N= 60 \implies \frac{N}{2} = 30

Now,
Given median = 28.5 which lies in the class 20-30

Therefore, Median class = 20-30
Frequency corresponding to median class, f = 20
Cumulative frequency of the class preceding the median class, c.f. = 5 + x
Lower limit, l = 20; Class height, h = 10

Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W
\\ \implies28.5= 20 + \left (\frac{30-5-x}{20} \right ).10 \\ \\ \implies8.5=\frac{25-x}{2} \\ \implies 25-x = 8.5(2) \\ \implies x = 25 - 17 = 8

Also,

\\ 60 = 45 + x+y \\ \implies x+y = 60-45 = 15 \\ \implies y = 15-x = 15-8 \ \ \ (\because x =8) \\ \implies y = 7

Therefore, the required values are: x=8 and y=7

Q3 A life insurance agent found the following data for the distribution of ages of 100 policyholders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 years.

1640762364185

Answer:

Class

Frequency

f_i

Cumulative

Frequency

15-20

2

2

20-25

4

6

25-30

18

24

30-35

21

45

35-40

33

78

40-45

11

89

45-50

3

92

50-55

6

98

55-60

2

100


N= 100 \implies \frac{N}{2} = 50
Therefore, Median class = 35-45
Frequency corresponding to median class, f = 21
Cumulative frequency of the class preceding the median class, c.f. = 24
Lower limit, l = 35; Class height, h = 10

Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W
\\ = 35 + \left (\frac{50-45}{33} \right ).5 \\ \\

= 35.75

Thus, the median age is 35.75 years.

Q4 The lengths of 40 leaves of a plant are measured correct to the nearest millimeter, and the data obtained is represented in the following table :

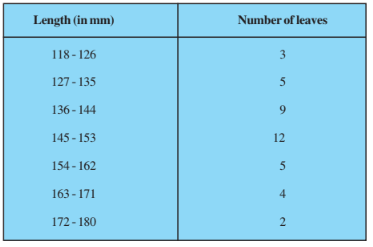
1640762380533

Find the median length of the leaves.
(Hint: The data needs to be converted to continuous classes for finding the median since the formula assumes continuous classes. The classes then change to
117.5 - 126.5, 126.5 - 135.5, . . ., 171.5 - 180.5.)

Answer:

The data needs to be converted to continuous classes for finding the median since the formula assumes continuous classes.

Class

Frequency

f_i

Cumulative

Frequency

117.5-126.5

3

3

126.5-135.5

5

8

135.5-144.5

9

17

144.5-153.5

12

29

153.5-162.5

5

34

162.5-171.5

4

38

171.5-180.5

2

40


\dpi{100} N= 40 \implies \frac{N}{2} = 20
Therefore, Median class = 144.5-153.5

Lower limit, l = 144.5; Class height, h = 9
Frequency corresponding to median class, f = 12
Cumulative frequency of the class preceding the median class, c.f. = 17

Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W
\\ = 144.5 + \left (\frac{20-17}{12} \right ).9 \\ \\

= 146.75

Thus, the median length of the leaves is 146.75 mm

Q5 The following table gives the distribution of the lifetime of 400 neon lamps :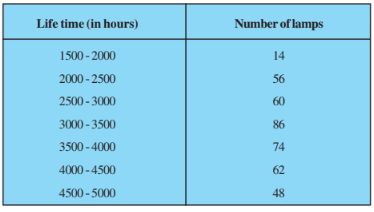
1640762410074


Find the median lifetime of a lamp.

Answer:

Class

Frequency

f_i

Cumulative

Frequency

1500-2000

14

14

2000-2500

56

70

2500-3000

60

130

3000-3500

86

216

3500-4000

74

290

4000-4500

62

352

4500-5000

48

400

\dpi{100} N= 400 \implies \frac{N}{2} = 200
Therefore, Median class = 3000-3500

Lower limit, l = 3000; Class height, h = 500
Frequency corresponding to median class, f = 86
Cumulative frequency of the class preceding the median class, c.f. = 130

Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W
\\ = 3000 + \left (\frac{200-130}{86} \right ).500 \\ \\ = 3000+406.97

= 3406.97

Thus, the median lifetime of a lamp is 3406.97 hours

= 146.75

Thus, the median length of the leaves is 146.75 mm

Q6 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

1640762454336

Determine the median number of letters in the surnames. Find the mean number of
letters in the surnames? Also, find the modal size of the surnames.

Answer:

Class

Number of

surnames f_i

Cumulative

Frequency

Classmark

x_i

f_ix_i

1-4

6

6

2.5

15

4-7

30

36

5.5

165

7-10

40

76

8.5

340

10-13

16

92

11.5

184

13-16

4

96

14.5

51

16-19

4

100

17.5

70



\sum f_i = N

= 100


\sum f_ix_i

= 825

MEDIAN:
N= 100 \implies \frac{N}{2} = 50
\therefore Median class = 7-10; Lower limit, l = 7;

Cumulative frequency of preceding class, c.f. = 36; f = 40; h = 3
Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W
\\ = 7+ \left (\frac{50-36}{40} \right ).3 \\ \\

= 8.05

Thus, the median of the data is 8.05

MODE:

The class having maximum frequency is the modal class.
The maximum frequency is 40 and hence the modal class = 7-10
Lower limit (l) of modal class = 7, class size (h) = 3
Frequency ( f_1 ) of the modal class = 40; frequency ( f_0 ) of class preceding the modal class = 30, frequency ( f_2 ) of class succeeding the modal class = 16

Mode = l + \left(\frac{f_1-f_0}{2f_1 - f_0 - f_2} \right).h

\\ = 7 + \left(\frac{40-30}{2(40)-30-16} \right).3 \\ \\ = 125 + \frac{10}{34}.3

= 7.88

Thus, Mode of the data is 7.88

MEAN:

Mean,
\overline x =\frac{\sum f_ix_i}{\sum f_i}
= \frac{825}{100} = 8.25

Thus, the Mean of the data is 8.25

Q7 The distribution below gives the weights of 30 students of a class. Find the median weight of the students.

1640762471389

Answer:

Class

Number of

students f_i

Cumulative

Frequency

40-45

2

2

45-50

3

5

50-55

8

13

55-60

6

19

60-65

6

25

65-70

3

28

70-75

2

30

MEDIAN:
N= 30 \implies \frac{N}{2} = 15
\therefore Median class = 55-60; Lower limit, l = 55;

Cumulative frequency of preceding class, c.f. = 13; f = 6; h = 5
Median = l + \left (\frac{\frac{n}{2}-c.f}{f} \right ).W
\\ = 55+ \left (\frac{15-13}{6} \right ).5 \\ \\ = 55+\frac{2}{6}.5

= 56.67

Thus, the median weight of the student is 56.67 kg



More About NCERT Solutions for Class 10 Maths Exercise 14.3

Class 10 Maths chapter 14 exercise 14 includes some of the basic questions in which we have to find the median of the grouped data. Along with this NCERT solutions for Class 10 Maths exercise 14.3 includes questions in which there is no class and we have to form the class of data ourselves. We also have to find all the central tendencies for some of the questions.

Exercise 14.3 Class 10 Maths covers all types of questions that can be formed in the median of grouped data and it has the question in which we have to find the frequency of the specific modal class. Moreover, there are few examples before NCERT solutions for Class 10 Maths exercise 14.3 that have questions that are based on the relation of mean, median and mode.

Also Read| Statistics Class 10 Notes

Benefits of NCERT Solutions for Class 10 Maths Exercise 14.3

  • Chapter 14 exercise 14.3 in Class 10 Maths presents a wide range of issues that might be based on a central tendency median, particularly on grouped data.
  • NCERT Statistics is a big element of the NCERT curriculum for Class 10 Mathematics chapter 14 exercise 14.3. It will be useful in JEE Main (joint admission exam) as statistics is a major part of the syllabus.
  • Class 10 Mathematics chapter 14 exercise 14.3 will serve as a foundation for Class 11 statistics chapter 15 (which is a continuation of this chapter).
  • The median can be used as a measure of location when one attaches reduced importance to extreme values

Key Features For Class 10 Maths Chapter 14 Exercise 14.3

  • Step-by-Step Solutions: Clear and detailed explanations for each problem in Ex 14.3 class 10, ensuring students understand the methodology.
  • Conceptual Understanding: Explanation of statistical concepts involved in the exercises, aiding students in grasping the underlying principles are discussed in class 10 maths ex 14.3.
  • Variety of Problems: In class 10 ex 14.3, diverse types of problems, offering a broad spectrum of challenges to reinforce understanding.
  • Visual Aids, Diagrams, and Examples: Use of visual representations, diagrams, and real-life examples to simplify complex concepts and aid visual learners.
  • Application-Based Problems: In10th class maths exercise 14.3 answers, application-oriented problems that relate statistics to real-world scenarios, fostering practical understanding and problem-solving skills.

Also, See:

NCERT Solutions for Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. How does the median depend on the number of observations?

Median gives the value of the observation which is at the center so it is dependent on either the observation is odd number or even number. Practice ex 14.3 class 10 to command these concepts.

2. What is the formula of median of odd observation ?

The concept related to discusses in class 10 ex 14.3. Formula of median of odd observation is  n/2th observation. Students can practice ex 14.3 class 10 to get deeper understanding of concepts.

3. What is the formula of median of even observation?

The concepts related to median is discussed in class 10 maths ex 14.3. Formula of median of even observation is  (n/2+ 1 )th observation. Also practice class 10 ex 14.3 which is discussed in this article to get deeper understanding of the concepts.

4. What is the relation between mean, medium and mode as mentioned in Class 10 Maths chapter 14 exercise 14.3?

3 Median = Mode + 2 Mean  is the relation between mean, medium and mode as mentioned in Class 10 maths chapter 14 exercise 14.3. 

5. What do you mean by Cumulative Frequency Table ?

These concepts are discussed in 10th class maths exercise 14.3 answers. practice them to command the concepts. Cumulative Frequency Table is the cumulative frequency is calculated by adding each frequency from a frequency distribution table to the sum of its predecessors.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Gujarat Board Secondary School Certificate Examination

Late Fee Application Date:11 December,2024 - 20 December,2024

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Business Analytics Foundations
 Via PW Skills
Digital Banking Business Model
 Via State Bank of India
Full-Stack Android Development
 Via Masai School
Data Science for Beginners
 Via Board Infinity
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
November 20, 2024 - 11:18 PM IST :
Board Exam Date 2025 Live: Bihar Class 10, 12 model papers out, time table soon; updates on CBSE, UP
December 06, 2024 - 10:42 PM IST
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST

Stay up-to date with CBSE Class 10th News

Back to top