Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 14.1 Class 10 Maths Chapter 14 - Statistics

NCERT Solutions for Exercise 14.1 Class 10 Maths Chapter 14 - Statistics

Updated on Apr 24, 2025 08:34 AM IST | #CBSE Class 10th

Statistics enables us to understand real-life data through interpretation of collected information. This field in mathematics handles the process of gathering numerical data followed by visual or analytical interpretation to reveal statistical patterns. The exercise works with grouped data together with frequency distribution patterns to analyze large statistical information. The procedure of grouping data followed by counting the number of occurrences in each category enables us to find significant patterns.

This Story also Contains
  1. NCERT Solutions Class 10 Maths Chapter 13: Exercise 13.1
  2. Topics covered in Chapter 13 Statistics: Exercise 13.1
  3. NCERT Solutions for Class 10 Subject Wise
  4. NCERT Exemplar Solutions of Class 10 Subject Wise
NCERT Solutions for Exercise 14.1 Class 10 Maths Chapter 14 - Statistics
NCERT Solutions for Exercise 14.1 Class 10 Maths Chapter 14 - Statistics

The NCERT Solutions for Exercise 14.1 represent unprocessed data through grouped frequency tables. The frequency tables demonstrate to students which values occur in which intervals. The exercise challenges students to convert raw data into structured forms which lays a foundation for computing mean, median and mode values in future assignments. The exercise functions as an essential tool for knowledge described in NCERT Books which leads to complete understanding of problems and their practical applications.

Background wave

NCERT Solutions Class 10 Maths Chapter 13: Exercise 13.1

Q1 A survey was conducted by a group of students as a part of their environment awareness program, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

1

Which method did you use for finding the mean, and why?

Answer:

Number of plants


Number of houses

fi

Classmark

xi

fixi

0-2

1

1

1

2-4

2

3

6

4-6

1

5

5

6-8

5

7

35

8-10

6

9

54

10-12

2

11

22

12-14

3

13

39


∑fi

=20


∑fixi

=162

Mean,

x―=∑fixi∑fi

=16220=8.1

We used the direct method in this as the values of xi and fi are small.

Q2 Consider the following distribution of daily wages of 50 workers of a factory. Find the mean daily wages of the workers of the factory by using an appropriate method.
2

Answer:

Let the assumed mean be a = 550

Daily

Wages

Number of

workers fi

Classmark

xi

di=xi−a

fidi

500-520

12

510

-40

-480

520-540

14

530

-20

-280

540-560

8

550

0

0

560-580

6

570

20

120

580-600

10

590

40

400


∑fi

= 50



∑fixi

= -240

Mean,

x―=a+∑fidi∑fi

=550+−24050=550−4.8=545.20

Therefore, the mean daily wages of the workers of the factory is Rs. 545.20

Q3 Following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.

3

Answer:

Daily pocket

allowance

Number of

children fi

Classmark

xi

fixi

11-13

7

12

84

13-15

6

14

84

15-17

9

16

144

17-19

13

18

234

19-21

f

20

20f

21-23

5

22

110

23-25

4

24

96


∑fi

=44+f


∑fixi

=752+20f

Mean,

x―=∑fixi∑fi

⟹18=752+20f44+f

⟹18(44+f)=(752+20f)⟹2f=40⟹f=20

Therefore the missing f = 20

Q4 Thirty women were examined in a hospital by a doctor and the number of heartbeats per minute was recorded and summarised as follows. Find the mean heartbeats per minute for these women, choosing a suitable method.

1636093324773

Answer:

Let the assumed mean be a = 75.5

No. of heartbeats

per minute

Number of

women fi

Classmark

xi

di=xi−a

fidi

65-68

2

66.5

-9

-18

68-71

4

69.5

-6

-24

71-74

3

72.5

-3

-9

74-77

8

75.5

0

0

77-80

7

78.5

3

21

80-83

4

81.5

6

24

83-86

2

84.5

9

18


∑fi

=30



∑fixi

=12

Mean,

x―=a+∑fidi∑fi

=75.5+1230=75.5+0.4=75.9

Therefore, the mean heartbeats per minute of these women are 75.9

Q5 In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying numbers of mangoes. The following was the distribution of mangoes according to the number of boxes.

5

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?

Answer:

Let the assumed mean be a = 57

Number of

mangoes

Number of

boxes fi

Classmark

xi

di=xi−a

fidi

50-52

15

51

-6

-90

53-55

110

54

-3

-330

56-58

135

57

0

0

59-61

115

60

3

345

62-64

25

63

6

150


∑fi

=400



∑fixi

=75

Mean,

x―=a+∑fidi∑fi

=57+75400=57+0.1875=57.1875≈57.19

Therefore, the mean number of mangoes kept in a packing box is approx 57.19

Q6 The table below shows the daily expenditure on the food of 25 households in a locality. Find the mean daily expenditure on food by a suitable method.

Daily expenditure in rupees

100-150150-200200-250250-300300-350
Number of households451222


Answer:

Let the assumed mean be a = 225 and h = 50

Daily

Expenditure

Number of

households fi

Classmark

xi

di=xi−a

ui=dih

fiui

100-150

4

125

-100

-2

-8

150-200

5

175

-50

-1

-5

200-250

12

225

0

0

0

250-300

2

275

50

1

2

300-350

2

325

100

2

4


∑fi

=25




∑fixi

= -7

Mean,

x―=a+∑fiui∑fi×h

=225+−725×50=225−14=211

Therefore, the mean daily expenditure on food is Rs. 211

Q7 To find out the concentration of SO2 in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below:
7

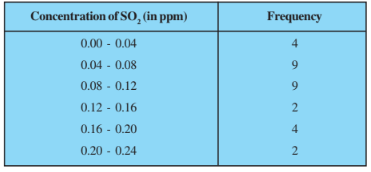
Find the mean concentration of SO2 in the air.

Answer:

Class

Interval

Frequency

fi

Classmark

xi

fixi

0.00-0.04

4

0.02

0.08

0.04-0.08

9

0.06

0.54

0.08-0.12

9

0.10

0.90

0.12-0.16

2

0.14

0.28

0.16-0.20

4

0.18

0.72

0.20-0.24

2

0.22

0.44


∑fi

=30


∑fixi

=2.96

Mean,

x―=∑fixi∑fi

=2.9630=0.099

Therefore, the mean concentration of SO2 in the air is 0.099 ppm

Q8 A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

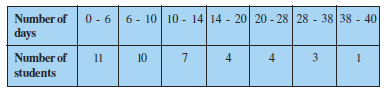
1636093576677

Answer:

Number of

days

Number of

Students fi

Classmark

xi

fixi

0-6

11

3

33

6-10

10

8

80

10-14

7

12

84

14-20

4

17

68

20-28

4

24

96

28-38

3

33

99

38-40

1

39

39






∑fi

=40


∑fixi

=499

Mean,

x―=∑fixi∑fi

=49940=12.475 =49940=12.475≈12.48

Therefore, the mean number of days a student was absent is 12.48 days.

Q9 The following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate.

9

Answer:

Let the assumed mean be a = 75 and h = 10

Literacy

rates

Number of

cities fi

Classmark

xi

di=xi−a

ui=dih

fiui

45-55

3

50

-20

-2

-6

55-65

10

60

-10

-1

-10

65-75

11

70

0

0

0

75-85

8

80

10

1

8

85-95

3

90

20

2

6


∑fi

= 35




∑fixi

= -2

Mean,

x―=a+∑fiui∑fi×h

=70+−235×10=70−0.57=69.43

Therefore, the mean mean literacy rate is 69.43%




Also Read-

NEET/JEE Coaching Scholarship

Get up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes

Apply
JEE Main high scoring chapters and topics

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

Get now

Topics covered in Chapter 13 Statistics: Exercise 13.1

1. Grouped Frequency Distribution: A person must learn to convert extensive raw data into classification intervals combined with frequency counts that produce better reading metrics.

2. Mid-point Method: The average calculation for grouped data requires using the midpoints from class intervals to estimate the central value.

3. Mean of Grouped Data: The formula Mean = (∑fx) / ∑f applies to calculate grouped data average while recognizing f as the frequency and x as the class mark (midpoint).

4. Data Interpretation: The skill involves understanding real-world data followed by tabular structure implementation for better analysis purposes.

5. Practical Understanding of Statistics: Data handling abilities prove essential in practical conditions like budgeting surveys and planning and budget processes.

Check Out-

NEET/JEE Offline Coaching
Get up to 90% Scholarship on your NEET/JEE preparation from India’s Leading Coaching Institutes like Aakash, ALLEN, Sri Chaitanya & Others.
Apply Now

NCERT Solutions for Class 10 Subject Wise

JEE Main Important Mathematics Formulas

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

Get now

NCERT Exemplar Solutions of Class 10 Subject Wise

Students must check the NCERT Exemplar solutions for class 10 of the Mathematics and Science Subjects.

Frequently Asked Questions (FAQs)

1. What is the main concept of Class 10 Maths chapter 14 exercise 14.1?

To find what is the basics of statistic. Definition of mean and its formula.  To learn about different methods of finding mean like Assumed mean method, step deviation method etc. Go through the ex 14.1 class 10 to command these concepts.

2. What do you understand by the mean of a set of data?

The mean (average) of a data set is found by adding all numbers in the data set and then dividing by the number of values in the set. Practice class 10 maths ex 14.1 to command these concepts.

3. What is class mark?

The class midpoint (or class mark) is a specific point in the centre of the bins (categories) in a frequency distribution table. Go through exercise 14.1 class 10 maths to get deeper understanding of concepts.

4. Find the mean of the data?

This class 10 ex 14.1 discusses the concept of mean in detail. to find mean of data use formula discussed in this exercise. mean = sum of total data / number of data

5. The centre of a bar in a histogram is known as?

The centre of a bar in a histogram is known as class mark.

6. What will happen to the mean of the data if every data set has increased by the value of 5?

The mean of the data will also increase by 5.

7. A data set has few intervals, one of such intervals is between 20 and 40. Find the class mark of this interval?

The mean of the data will also increase by 5.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Admit Card Date:02 April,2025 - 19 May,2025

National Institute of Open Schooling 12th Examination

Admit Card Date:02 April,2025 - 19 May,2025

National Means Cum-Merit Scholarship

Application Date:13 April,2025 - 30 April,2025

Goa Board Higher Secondary School Certificate Examination

Admit Card Date:17 April,2025 - 17 May,2025

Telangana Open School Society Intermediate Examination

Exam Date:26 April,2025 - 03 May,2025

View All School Exams

Certifications By Top Providers

Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
i studied 1 to 10th CBSE board abroad and 11th 12th in karnataka state board . i am a domicile of karnataka and comes under minority, income under 5 lakhs. how neet councillng will allocate my seat

Hello

Since you are a domicile of Karnataka and have studied under the Karnataka State Board for 11th and 12th , you are eligible for Karnataka State Quota for admission to various colleges in the state.

1. KCET (Karnataka Common Entrance Test): You must appear for the KCET exam, which is required for admission to undergraduate professional courses like engineering, medical, and other streams. Your exam score and rank will determine your eligibility for counseling.

2. Minority Income under 5 Lakh : If you are from a minority community and your family's income is below 5 lakh, you may be eligible for fee concessions or other benefits depending on the specific institution. Some colleges offer reservations or other advantages for students in this category.

3. Counseling and Seat Allocation:

After the KCET exam, you will need to participate in online counseling.

You need to select your preferred colleges and courses.

Seat allocation will be based on your rank , the availability of seats in your chosen colleges and your preferences.

4. Required Documents :

Domicile Certificate (proof that you are a resident of Karnataka).

Income Certificate (for minority category benefits).

Marksheets (11th and 12th from the Karnataka State Board).

KCET Admit Card and Scorecard.

This process will allow you to secure a seat based on your KCET performance and your category .

check link for more details

https://medicine.careers360.com/neet-college-predictor

Hope this helps you .

Read Complete Answer
Mitali Sharma 30 January,2025
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Study Resources, Applications and Opportunities

ALLEN Coaching
ALLEN Coaching
Apply

Register for ALLEN Scholarship Test & get up to 90% Scholarship

NEET/JEE Coaching Scholarship
NEET/JEE Coaching Scholarship
Apply

Get up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes

NEET Most scoring concepts
NEET Most scoring concepts
Get now

This ebook serves as a valuable study guide for NEET 2025 exam.

NEET Previous 10 Year Questions
NEET Previous 10 Year Questions
Get now

This e-book offers NEET PYQ and serves as an indispensable NEET study material.

JEE Main Important Physics formulas
Get now

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Get now

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

View All Application Forms
News and Notifications
CBSE 10th Result 2025: Evaluation criteria, marking scheme, supplementary exams; what we know
March 31, 2025 - 03:51 PM IST
Holding CBSE Class 10 twice can lead to ‘paper leaks, irregularities’, warns parliament panel
March 27, 2025 - 11:00 AM IST
When will CBSE Class 10 results 2025 be declared? Overall exam paper analysis
March 22, 2025 - 03:58 PM IST
CBSE will rope in external agency for skill, vocational subject exams
March 22, 2025 - 12:23 PM IST
CBSE adopts new re-evaluation process, split Class 10 science question papers; will test on-screen marking
March 21, 2025 - 06:10 PM IST
CBSE Board Exam 2025 Live: Class 10 CS, IT, AI paper 'easy, straightforward'; difficulty level, answer key
March 18, 2025 - 09:58 PM IST
CBSE Class 10 CS, IT AI Exam Analysis 2025: Paper 'easy, well-balanced'; section-wise difficulty level
March 18, 2025 - 03:04 PM IST

Stay up-to date with CBSE Class 10th News

Back to top